2023年高考数学复习专题课件★★应用性考法 课件(共29张PPT)
文档属性
| 名称 | 2023年高考数学复习专题课件★★应用性考法 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-31 11:53:32 | ||
图片预览







文档简介
(共29张PPT)
2023年高考数学复习专题课件★★) 应用性考法
[4“步”建模]
[4“步”建模]
[4“步”建模]
[4“步”建模]
[4“步”建模]
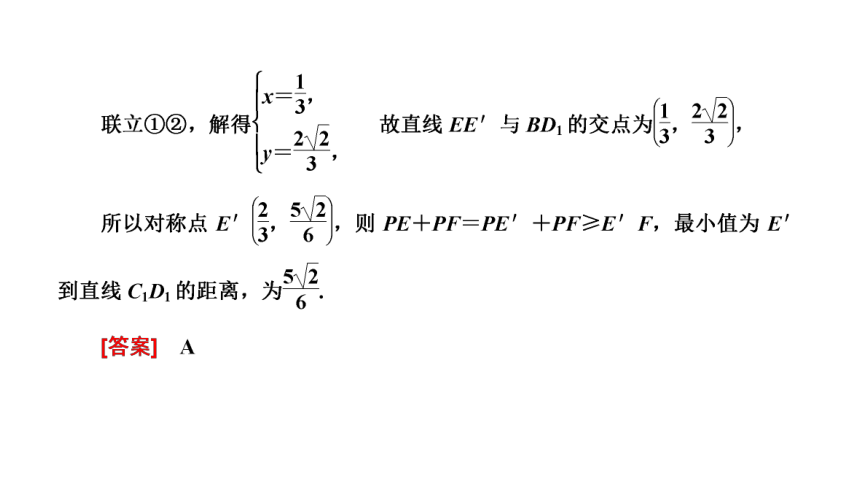
解析:以圆拱桥的顶点为坐标原点,建立如图所示的平面直角坐标系,
则圆拱所在圆的圆心位于y轴负半轴上,设该圆的圆心为(0,
-a),a>0,
则该圆的方程为x2+(y+a)2=a2,
记水面下降前与圆的两交点为A,B;记水面下降1 m后与圆的两交点为C,D;
2.如图所示,“嫦娥五号”月球探测器飞行到月球附近时,首先
在以月球球心F为圆心的圆形轨道Ⅰ上绕月球飞行,然后在P
点处变轨进入以F为一个焦点的椭圆轨道Ⅱ绕月球飞行,最后
在Q点处变轨进入以F为圆心的圆形轨道Ⅲ绕月球飞行,设圆形轨道Ⅰ的半径为R,圆形轨道Ⅲ的半径为r,则下列结论中正确的序号为 ( )
①轨道Ⅱ的焦距为R-r;②若R不变,r越大,轨道Ⅱ的短轴长越小;③轨道Ⅱ的长轴长为R+r;④若r不变,R越大,轨道Ⅱ的离心率越大.
A.①②③ B.①②④
C.①③④ D.②③④
模型
题中元素涉及圆、抛物线及其方程和它们的公
准备
切线
模型
联想到圆和所求的抛物线有公切线,据此可求抛
假设
物线的方程
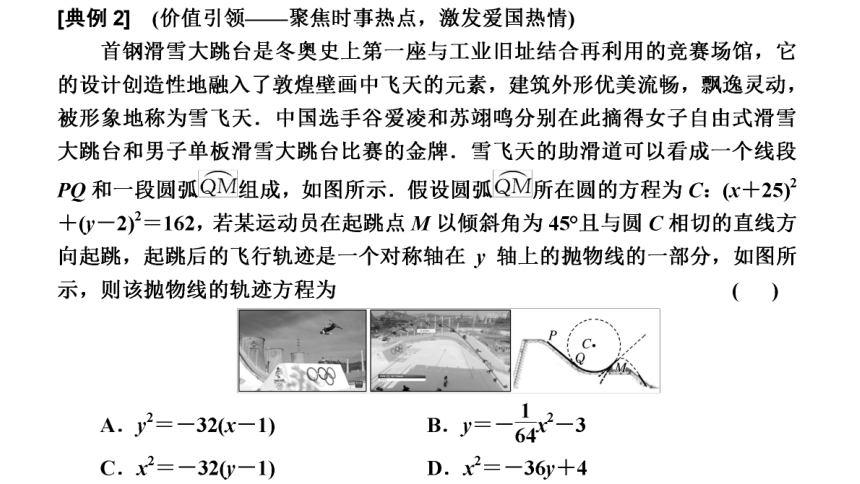
由题意可得到直线CM所在的方程,和圆的方程
模型
联立求得点M的坐标,设所求抛物线方程y=
建立
αx2十c,由倾斜角为45°,知切线斜率为1,求导
得a的值进而求得c
模型
题中元素有椭圆、抛物线,数轴上两,点的距离
准备
模型
设抛物线的方程
假设
设点B所在的抛物线方程为y=ax2十
36
,代入
模型
建立
,点C(6,4),可求方程,令y=0,解得x=9,根据
AB=OB-OA,即可求解
模型
题中元素有双曲线的离心率,青花瓷瓶颈部中最
准备
细处直径为16cm,瓶口直径为20cm
模型
因为有了双曲线的一些数据,故联想到求其方
假设
程,利用方程求花瓶的颈部高
2
设双曲线方程为
2
=1(a0,b0),根据已知
模型
建立
条件可得,c的值,由=2一可得双曲线的方
程,再将x=10代入方程可得y的值,即可求解
模型
题中元素有椭圆的焦,点、离心率、焦距
淮备
模型
联想到题中数据,可以求出椭圆的实轴长,进而
假设得出光线的路程
2
2
设椭圆的方程为
y
6
=1(ab0),进而根据
L
模型
5
建立
题意得e=
,2c=5,故2a=9,再根据椭圆
的定义求解即可
2023年高考数学复习专题课件★★) 应用性考法
[4“步”建模]
[4“步”建模]
[4“步”建模]
[4“步”建模]
[4“步”建模]
解析:以圆拱桥的顶点为坐标原点,建立如图所示的平面直角坐标系,
则圆拱所在圆的圆心位于y轴负半轴上,设该圆的圆心为(0,
-a),a>0,
则该圆的方程为x2+(y+a)2=a2,
记水面下降前与圆的两交点为A,B;记水面下降1 m后与圆的两交点为C,D;
2.如图所示,“嫦娥五号”月球探测器飞行到月球附近时,首先
在以月球球心F为圆心的圆形轨道Ⅰ上绕月球飞行,然后在P
点处变轨进入以F为一个焦点的椭圆轨道Ⅱ绕月球飞行,最后
在Q点处变轨进入以F为圆心的圆形轨道Ⅲ绕月球飞行,设圆形轨道Ⅰ的半径为R,圆形轨道Ⅲ的半径为r,则下列结论中正确的序号为 ( )
①轨道Ⅱ的焦距为R-r;②若R不变,r越大,轨道Ⅱ的短轴长越小;③轨道Ⅱ的长轴长为R+r;④若r不变,R越大,轨道Ⅱ的离心率越大.
A.①②③ B.①②④
C.①③④ D.②③④
模型
题中元素涉及圆、抛物线及其方程和它们的公
准备
切线
模型
联想到圆和所求的抛物线有公切线,据此可求抛
假设
物线的方程
由题意可得到直线CM所在的方程,和圆的方程
模型
联立求得点M的坐标,设所求抛物线方程y=
建立
αx2十c,由倾斜角为45°,知切线斜率为1,求导
得a的值进而求得c
模型
题中元素有椭圆、抛物线,数轴上两,点的距离
准备
模型
设抛物线的方程
假设
设点B所在的抛物线方程为y=ax2十
36
,代入
模型
建立
,点C(6,4),可求方程,令y=0,解得x=9,根据
AB=OB-OA,即可求解
模型
题中元素有双曲线的离心率,青花瓷瓶颈部中最
准备
细处直径为16cm,瓶口直径为20cm
模型
因为有了双曲线的一些数据,故联想到求其方
假设
程,利用方程求花瓶的颈部高
2
设双曲线方程为
2
=1(a0,b0),根据已知
模型
建立
条件可得,c的值,由=2一可得双曲线的方
程,再将x=10代入方程可得y的值,即可求解
模型
题中元素有椭圆的焦,点、离心率、焦距
淮备
模型
联想到题中数据,可以求出椭圆的实轴长,进而
假设得出光线的路程
2
2
设椭圆的方程为
y
6
=1(ab0),进而根据
L
模型
5
建立
题意得e=
,2c=5,故2a=9,再根据椭圆
的定义求解即可
同课章节目录
