2023届高考数学复习专题★★立体几何中的范围(最值)问题 课件(共30张PPT)
文档属性
| 名称 | 2023届高考数学复习专题★★立体几何中的范围(最值)问题 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-05 10:13:26 | ||
图片预览











文档简介
(共30张PPT)
2023届高考数学复习专题★★
立体几何中的范围(最值)问题
解决空间图形有关的线段、角、距离、面积、体积等最值问题,一般可以从三方面着手:一是从问题的几何特性入手,充分利用其几何性质去解决;二是利用空间几何体的侧面展开图;三是找出问题中的代数关系,建立目标函数,利用代数方法求目标函数的最值.解题途径很多,在函数建成后,可用一次函数的端点法,二次函数的配方法、公式法,函数有界法(如三角函数等)及高阶函数的拐点导数法等.
技法1 几何特性法
例1 如图,在三棱锥
若点
值为( )
A.
√
解析:连接
所以
又
则点
连接
点
所以
本题是利用几何性质求解,由于点
牙雕套球又称“鬼工球”,“鬼工”即鬼斧神工的意思,制作相当
繁杂,工艺要求极高.现有某“鬼工球”,由外及里是两层表面积
分别为
A.
球壁的厚度忽略不计),在外球表面上有一点
连接
√
解析:选C.设外球的半径为
面积为
如图,作过外球表面上一点
因为线段
则线段
技法2 侧面展开图法
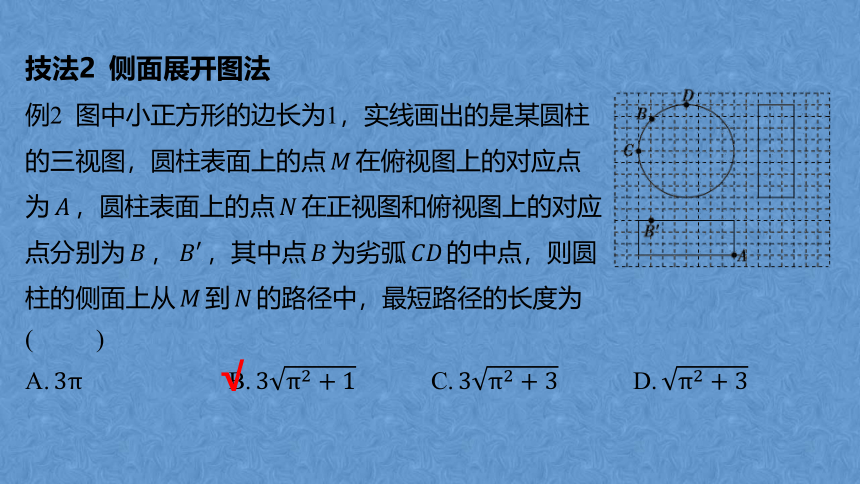
例2 图中小正方形的边长为1,实线画出的是某圆柱
的三视图,圆柱表面上的点
为
点分别为
柱的侧面上从
( )
A.
√
解析:根据三视图作出圆柱的示意图,如图
(1)所示,其中
影,
,
则
本题利用圆柱的侧面展开图,把空间问题转化为平面问题,即两点之间线段最短.
(2022·广东佛山教学质量检测(一))在长方体
则四边形
A.
√
解析:选B.作出长方体如图1,将侧面展
开,如图2所示,当点
交点,
四边形
最小值为
技法3 目标函数法
例3 (2022·新高考卷Ⅰ)已知正四棱锥的侧棱长为
球面上.若该球的体积为
范围是( )
A.
√
解析:通解:如图,设该球的球心为
解得
所以正四棱锥的体积
所以函数
光速解:如图,设该球的球心为
解得
优美解:如图,设该球的半径为
&1&
本题利用目标函数法求体积最值,其思路为:
设球心到正四棱锥底面中心的长度为
1.如图,是一个底面半径和高都是1的圆锥形容器,匀速给
容器注水,则容器中水的体积
记为
最小值为_ __.
解析:因为圆锥形容器的底面半径和高都是1,水面高度为,
2.如图,四棱锥
积最大的圆柱,则剩余几何体的表面积等于
_____________.
解析:如图,在四棱锥
其中点
连接
连接
即
故挖掉的圆柱的体积
所以
当
所以当
即剩余几何体的表面积
2023届高考数学复习专题★★
立体几何中的范围(最值)问题
解决空间图形有关的线段、角、距离、面积、体积等最值问题,一般可以从三方面着手:一是从问题的几何特性入手,充分利用其几何性质去解决;二是利用空间几何体的侧面展开图;三是找出问题中的代数关系,建立目标函数,利用代数方法求目标函数的最值.解题途径很多,在函数建成后,可用一次函数的端点法,二次函数的配方法、公式法,函数有界法(如三角函数等)及高阶函数的拐点导数法等.
技法1 几何特性法
例1 如图,在三棱锥
若点
值为( )
A.
√
解析:连接
所以
又
则点
连接
点
所以
本题是利用几何性质求解,由于点
牙雕套球又称“鬼工球”,“鬼工”即鬼斧神工的意思,制作相当
繁杂,工艺要求极高.现有某“鬼工球”,由外及里是两层表面积
分别为
A.
球壁的厚度忽略不计),在外球表面上有一点
连接
√
解析:选C.设外球的半径为
面积为
如图,作过外球表面上一点
因为线段
则线段
技法2 侧面展开图法
例2 图中小正方形的边长为1,实线画出的是某圆柱
的三视图,圆柱表面上的点
为
点分别为
柱的侧面上从
( )
A.
√
解析:根据三视图作出圆柱的示意图,如图
(1)所示,其中
影,
则
本题利用圆柱的侧面展开图,把空间问题转化为平面问题,即两点之间线段最短.
(2022·广东佛山教学质量检测(一))在长方体
则四边形
A.
√
解析:选B.作出长方体如图1,将侧面展
开,如图2所示,当点
交点,
四边形
最小值为
技法3 目标函数法
例3 (2022·新高考卷Ⅰ)已知正四棱锥的侧棱长为
球面上.若该球的体积为
范围是( )
A.
√
解析:通解:如图,设该球的球心为
解得
所以正四棱锥的体积
所以函数
光速解:如图,设该球的球心为
解得
优美解:如图,设该球的半径为
&1&
本题利用目标函数法求体积最值,其思路为:
设球心到正四棱锥底面中心的长度为
1.如图,是一个底面半径和高都是1的圆锥形容器,匀速给
容器注水,则容器中水的体积
记为
最小值为_ __.
解析:因为圆锥形容器的底面半径和高都是1,水面高度为
2.如图,四棱锥
积最大的圆柱,则剩余几何体的表面积等于
_____________.
解析:如图,在四棱锥
其中点
连接
连接
即
故挖掉的圆柱的体积
所以
当
所以当
即剩余几何体的表面积
同课章节目录
