2023届高考数学复习专题★★ 数列中的奇、偶项问题 课件(共19张PPT)
文档属性
| 名称 | 2023届高考数学复习专题★★ 数列中的奇、偶项问题 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-05 10:17:24 | ||
图片预览



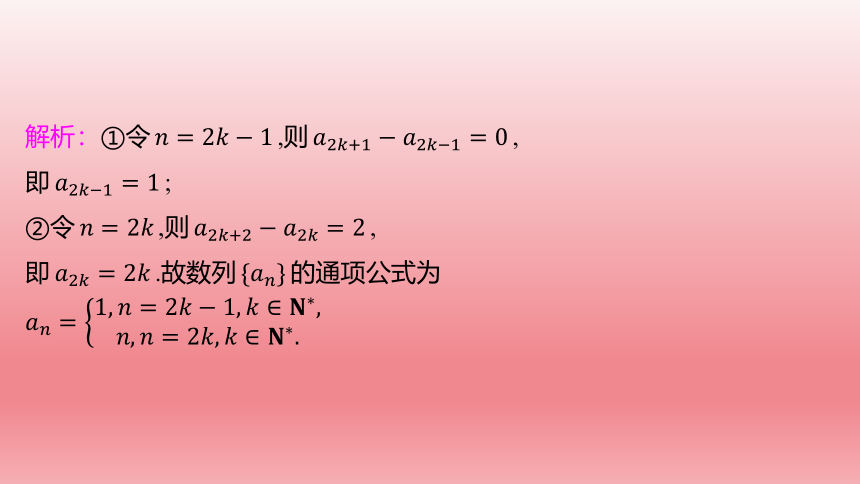



文档简介
(共19张PPT)
2023届高考数学复习专题★★
数列中的奇、偶项问题
1.数列中的奇、偶项问题的常见题型
(1)数列中连续两项和或积的问题
(2)含有
(3)含有
(4)已知条件明确的奇偶项问题.
2.对于通项公式分奇、偶项有不同表达式的数列
类型1 求数列的通项公式
例1 (1)数列
解析:①令
即
②令
即
(2)已知数列
式为____________.
解析:由题意,
由②-①得,
由
所以
当
当
综上所述,
数列中的奇、偶项问题的常见题型
(1)数列中连续两项和或积的问题
(2)含有
(3)含有
(4)已知条件明确的奇偶项问题.
1.若数列
A.
解析:选C.由
√
2.在数列
_____________________.
解析:由题意得
所以
所以
由②-①,得
所以
又因为
所以
综上所述,
类型2 求数列的和
例2 (1)(2022·宁夏石嘴山一中5月适应性考试)已知数列
528
解析:当
当
所以
(2)已知数列
解析:因为
当
当
所以
对于通项公式分奇、偶不同的数列
1.(2022·河南郑州二模)已知数列
的第2 022项为( )
A.
√
解析:选A.因为
所以
所以
所以
将上述各式累加,得
2.(2022·江苏南京高三学情调研)已知正项等比数列
(1)求
解:设等比数列
因为数列
因为
所以
又
即
因为
所以
又
所以
(2)若
[答案] 因为
所以
2.(2022·江苏南京高三学情调研)已知正项等比数列
2023届高考数学复习专题★★
数列中的奇、偶项问题
1.数列中的奇、偶项问题的常见题型
(1)数列中连续两项和或积的问题
(2)含有
(3)含有
(4)已知条件明确的奇偶项问题.
2.对于通项公式分奇、偶项有不同表达式的数列
类型1 求数列的通项公式
例1 (1)数列
解析:①令
即
②令
即
(2)已知数列
式为____________.
解析:由题意,
由②-①得,
由
所以
当
当
综上所述,
数列中的奇、偶项问题的常见题型
(1)数列中连续两项和或积的问题
(2)含有
(3)含有
(4)已知条件明确的奇偶项问题.
1.若数列
A.
解析:选C.由
√
2.在数列
_____________________.
解析:由题意得
所以
所以
由②-①,得
所以
又因为
所以
综上所述,
类型2 求数列的和
例2 (1)(2022·宁夏石嘴山一中5月适应性考试)已知数列
528
解析:当
当
所以
(2)已知数列
解析:因为
当
当
所以
对于通项公式分奇、偶不同的数列
1.(2022·河南郑州二模)已知数列
的第2 022项为( )
A.
√
解析:选A.因为
所以
所以
所以
将上述各式累加,得
2.(2022·江苏南京高三学情调研)已知正项等比数列
(1)求
解:设等比数列
因为数列
因为
所以
又
即
因为
所以
又
所以
(2)若
[答案] 因为
所以
2.(2022·江苏南京高三学情调研)已知正项等比数列
同课章节目录
