高考大题研究课九最值与范围问题-2023届高三数学(新教材)二轮复习 课件(共34张PPT)
文档属性
| 名称 | 高考大题研究课九最值与范围问题-2023届高三数学(新教材)二轮复习 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-05 21:21:33 | ||
图片预览




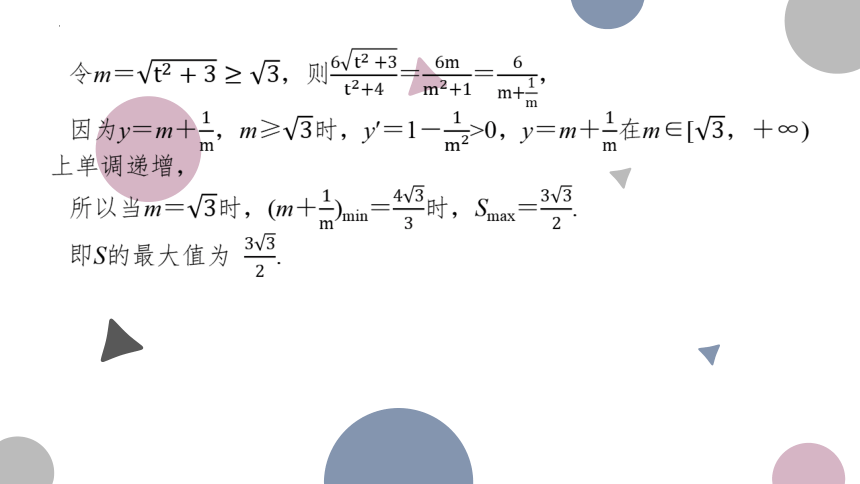






文档简介
(共34张PPT)
高考大题研究课九 最值与范围问题
题型一 最值问题
例1 [2023·安徽十校联考]如图,已知椭圆C:=1(a>b>0)的左、右顶点分别是A,B,且经过点(1,-),直线 l:x=ty-1恒过定点F且交椭圆于D,E两点,F为OA的中点.
(1)求椭圆C的标准方程;
(2)记△BDE的面积为S,求S的最大值.
解析:(1)由题意可得,直线l:x=ty-1恒过定点F(-1,0),
因为F为OA的中点,所以|OA|=2,即a=2.
因为椭圆C经过点 (1,-),所以 =1,解得b=1,
所以椭圆C的方程为+y2=1.
(2)设E(x1,y1),D(x2,y2).
由得(t2+4)y2-2ty-3=0,Δ>0恒成立,
则y1+y2=,y1y2=-,
则|ED|=·=·=,
又因为点B到直线l的距离d=,
所以S=×|ED|×d=··=.
令m=,则==,
因为y=m+,m≥时,y′=1->0,y=m+在m∈[,+∞)上单调递增,
所以当m=时,(m+)min=时,Smax=.
即S的最大值为 .
题后师说
解析几何中的常见最值问题有:线段长度(弦长)最值、三角形面积最值、面积比最值、线段长度比最值等.常用解题方法是把这些问题利用代数方法转化为关于某个变量的函数,然后通过一些变形:分式型函数常分离常数转化为x+(a>0)的形式、分子分母同时除以某个式子后转化为x+(a>0)的形式、先换元再转化为x+(a>0)形式;乘积型式子看能否通过“1”变形、拆项、添项等使得和为定值,进而利用基本不等式或其变形解决.
巩固训练1
(1)[2023·湖北监利期末]已知曲线C上任意一点P(x,y)满足方程||=2,
①求曲线C的方程;
②若直线l与曲线C在y轴左、右两侧的交点分别是Q,P,且·=0,求||2+||2的最小值.
解析:(1)①设F1(-,0),F2(,0),
则=2,等价于||PF1|-|PF2||=2<|F1F2|,
∴曲线C为以F1,F2为焦点的双曲线,且实轴长为2,焦距为2,
故曲线C的方程为x2-=1.
②由题意可得直线OP的斜率存在且不为0,可设直线OP的方程为y=kx(k≠0),
则直线OQ的方程为y=-x,由,得,
所以|OP|2=x2+y2=,同理可得,|OQ|2==,
所以===,|OP|2+|OQ|2=2(|OP|2+|OQ|2)()=2[2+()2+()2]≥2(2+2)=8,
当且仅当|OP|=|OQ|=2时取等号,
所以当|OP|=|OQ|=2时,|OP|2+|OQ|2取得最小值8.
(2)[2023·河南南阳期末]已知抛物线C:x2=2py(p>0)的通径长为,若抛物线C上有一动弦AB的中点为M,且弦AB的长度为3.
①求抛物线C的方程;
②求点M的纵坐标的最小值.
解析:(2)①由题意可知:2p=,所以抛物线C的方程为x2=y;
②由题意可知:直线AB斜率必存在,设其方程为y=kx+b.
设A(x1,y1),B(x2,y2),M(x0,y0).则x0=,y0=,
联立方程得2x2-kx-b=0.
所以,y1+y2=+2b.
又知:|AB|=
= =3,
得2b=,
∴y0==+2b)=)
=)≥(2)=.
当且仅当=,即k2=5时取等号,
则点M的纵坐标的最小值为.
题型二 范围问题
例2 [2023·广东揭阳期末]已知椭圆C:=1(a>b>0)的离心率为,点A()在椭圆C上.
(1)求椭圆C的标准方程;
(2)已知直线l:y=k(x-3)(k≠0)与椭圆C交于P,Q两点,点M是线段PQ的中点,直线l′过点M,且与直线l垂直.记直线l′与y轴的交点为N,求|MN|的取值范围.
解析:(1)由题意可得,解得a2=4,b2=3.
故椭圆C的标准方程为=1.
(2)设P(x1,y1),Q(x2,y2),M(x0,y0).
联立,整理得(4k2+3)x2-24k2x+36k2-12=0,
则Δ=(-24k2)2-4(4k2+3)(36k2-12)=48(3-5k2)>0,解得0从而x1+x2=,x1x2=.
因为M是线段PQ的中点,所以x0==,
则y0=k(x0-3)=-,故M(,-).
直线l′的方程为y-y0=-(x-x0),即y+=-(x-).
令x=0,得y=-(0-)-=,
则N(0,),
所以|MN|==.
设t=4k2+3,则k2=,
故|MN|==3=3.
因为0题后师说
解圆锥曲线中范围问题的策略
巩固训练2
(1)[2023·辽宁抚顺期末]已知椭圆C1的方程为=1,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.
(ⅰ)求双曲线C2的方程;
(ⅱ)若直线l:y=kx+2与双曲线C2恒有两个不同的交点A和B,且·>1(其中O为原点),求k的取值范围.
解析:(1)ⅰ由题,在椭圆C1中,焦点坐标为(-1,0)和(1,0);左右顶点为(-2,0)和(2,0),
因为双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点,
所以在双曲线C2中,设双曲线方程为=1,则a2=1,c2=4,所以b2=c2-a2=3,
所以双曲线C2的方程为x2-=1.
ⅱ由ⅰ联立,消去y,得(k2-3)x2+4kx+7=0;①
消去x,得(k2-3)y2+12y-12+3k2=0.②
设A(x1,y1),B(x2,y2),则x1,x2为方程①的两根,y1,y2为方程②的两根;
x1·x2=,y1·y2=,
·=x1·x2+y1·y2=>1,
得k2>3或k2<1,③
又因为方程①中,Δ=16k2-4×7(k2-3)=-12k2+84>0,得k2<7,④
③④联立得k的取值范围(-,-)∪(-1,1)∪(, ).
(2)[2023·湖北武汉模拟]已知动圆C过定点A(2,0),且在y轴上截得的弦长为4,圆心C的轨迹为曲线Γ.
(ⅰ)求Γ的方程;
(ⅱ)过点P(1,0)的直线l与Γ相交于M,N两点.设=λ,若λ∈[2,3],求l在y轴上截距的取值范围.
解析:(2)ⅰ设C(x,y),圆C的半径为R,则R2=22+x2=(x-2)2+(y-0)2整理,得y2=4x,所以Γ的方程为y2=4x.
ⅱ设M(x1,y1),N(x2,y2),又P(1,0),由=λ,得(x2-1,y2)=λ(1-x1,-y1)∴.由②,得==4x2∴x2=λ2x1③,联立①、③解得x2=λ,依题意有λ>0,∴N(λ,2)或N(λ,-2),又P(1,0),∴直线l的方程为(λ-1)y=2(x-1),或(λ-1)y=-2(x-1),当λ∈[2,3]时,l在y轴上的截距为或-,由=,可知在[2,3]上是单调递减的,∴≤2,-2≤-≤-,∴直线l在y轴上截距的取值范围为[-2,-∪,2].
真题展台
1.[2021·全国乙卷]已知抛物线C:y2=2px(p>0)的焦点F到准线的距离为2.
(1)求C的方程;
(2)已知O为坐标原点,点P在C上,点Q满足=9,求直线OQ斜率的最大值.
解析:(1)抛物线C:y2=2px(p>0)的焦点F(,0),准线方程为x=-,
由题意,该抛物线焦点到准线的距离为-(-)=p=2,
所以该抛物线的方程为y2=4x.
(2)设Q(x0,y0),则=9=(9-9x0,-9y0),
所以P(10x0-9,10y0),
由P在抛物线上可得(10y0)2=4(10x0-9),即x0=,
所以直线OQ的斜率kOQ===,
当y0=0时,kOQ=0;
当y0≠0时,kOQ=,当y0>0时,因为25y0+≥2=30,此时0当y0<0时,kOQ<0;综上,直线OQ的斜率的最大值为.
2.[2021·北京卷]已知椭圆E:=1(a>b>0)过点A(0,-2),以四个顶点围成的四边形面积为4.
(1)求椭圆E的标准方程;
(2)过点P(0,-3)的直线l斜率为k,交椭圆E于不同的两点B,C,直线AB,AC交y=-3于点M、N,若|PM|+|PN|≤15,求k的取值范围.
解析:(1)因为椭圆过A(0,-2),故b=2,
因为四个顶点围成的四边形的面积为4,故×2a×2b=4,即a=,
故椭圆的标准方程为=1.
(2)设B(x1,y1),C(x2,y2),
因为直线BC的斜率存在,故x1x2≠0,
故直线AB:y=x-2,令y=-3,
则xM=-,同理xN=-.
直线BC:y=kx-3,由可得(4+5k2)x2-30kx+25=0,
故Δ=900k2-100(4+5k2)>0,解得k<-1或k>1.
又x1+x2=,x1x2=,故x1x2>0,所以xMxN>0.
又|PM|+|PN|=|xM+xN|=||
=||=||=||=5|k|,
故5|k|≤15即|k|≤3,
综上,-3≤k<-1或13.[2020·新高考Ⅱ卷]已知椭圆C:=1(a>b>0)过点M(2,3),点A为其左顶点,且AM的斜率为.
(1)求C的方程;
(2)点N为椭圆上任意一点,求△AMN的面积的最大值.
解析:(1)由题意可知直线AM的方程为y-3=(x-2),即x-2y=-4.
当y=0时,解得x=-4,所以a=4.
椭圆C:=1(a>b>0)过点M(2,3),可得=1,解得b2=12.
所以C的方程:=1.
(2)设与直线AM平行的直线方程为x-2y=m,
如图所示,当直线与椭圆相切时,与AM距离比较远的直线与椭圆的切点为N,此时△AMN的面积取得最大值.
联立直线方程x-2y=m与椭圆方程=1,
可得3(m+2y)2+4y2=48,
化简可得16y2+12my+3m2-48=0,
所以Δ=144m2-4×16(3m2-48)=0,
即m2=64,解得m=±8,
与AM距离比较远的直线方程:x-2y=8,
直线AM方程为x-2y=-4,
点N到直线AM的距离即两平行线之间的距离,
利用平行线之间的距离公式可得d==,
由两点之间距离公式可得|AM|==3.
所以△AMN的面积的最大值为×3=18.
高考大题研究课九 最值与范围问题
题型一 最值问题
例1 [2023·安徽十校联考]如图,已知椭圆C:=1(a>b>0)的左、右顶点分别是A,B,且经过点(1,-),直线 l:x=ty-1恒过定点F且交椭圆于D,E两点,F为OA的中点.
(1)求椭圆C的标准方程;
(2)记△BDE的面积为S,求S的最大值.
解析:(1)由题意可得,直线l:x=ty-1恒过定点F(-1,0),
因为F为OA的中点,所以|OA|=2,即a=2.
因为椭圆C经过点 (1,-),所以 =1,解得b=1,
所以椭圆C的方程为+y2=1.
(2)设E(x1,y1),D(x2,y2).
由得(t2+4)y2-2ty-3=0,Δ>0恒成立,
则y1+y2=,y1y2=-,
则|ED|=·=·=,
又因为点B到直线l的距离d=,
所以S=×|ED|×d=··=.
令m=,则==,
因为y=m+,m≥时,y′=1->0,y=m+在m∈[,+∞)上单调递增,
所以当m=时,(m+)min=时,Smax=.
即S的最大值为 .
题后师说
解析几何中的常见最值问题有:线段长度(弦长)最值、三角形面积最值、面积比最值、线段长度比最值等.常用解题方法是把这些问题利用代数方法转化为关于某个变量的函数,然后通过一些变形:分式型函数常分离常数转化为x+(a>0)的形式、分子分母同时除以某个式子后转化为x+(a>0)的形式、先换元再转化为x+(a>0)形式;乘积型式子看能否通过“1”变形、拆项、添项等使得和为定值,进而利用基本不等式或其变形解决.
巩固训练1
(1)[2023·湖北监利期末]已知曲线C上任意一点P(x,y)满足方程||=2,
①求曲线C的方程;
②若直线l与曲线C在y轴左、右两侧的交点分别是Q,P,且·=0,求||2+||2的最小值.
解析:(1)①设F1(-,0),F2(,0),
则=2,等价于||PF1|-|PF2||=2<|F1F2|,
∴曲线C为以F1,F2为焦点的双曲线,且实轴长为2,焦距为2,
故曲线C的方程为x2-=1.
②由题意可得直线OP的斜率存在且不为0,可设直线OP的方程为y=kx(k≠0),
则直线OQ的方程为y=-x,由,得,
所以|OP|2=x2+y2=,同理可得,|OQ|2==,
所以===,|OP|2+|OQ|2=2(|OP|2+|OQ|2)()=2[2+()2+()2]≥2(2+2)=8,
当且仅当|OP|=|OQ|=2时取等号,
所以当|OP|=|OQ|=2时,|OP|2+|OQ|2取得最小值8.
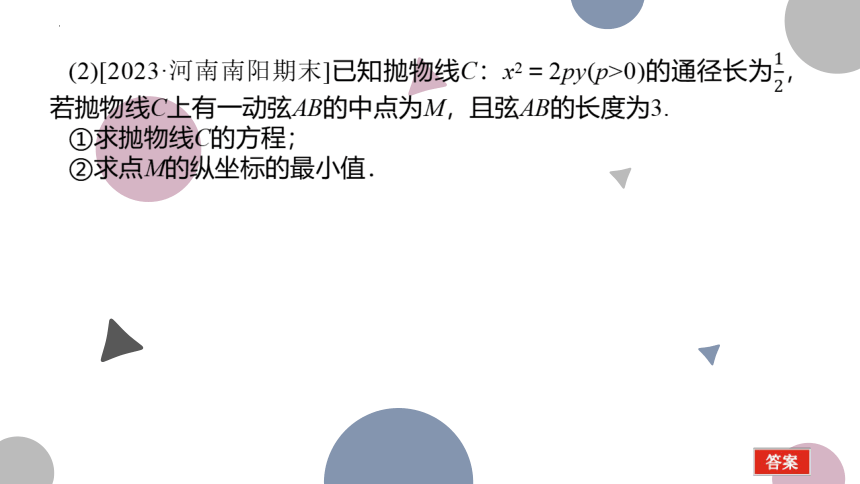
(2)[2023·河南南阳期末]已知抛物线C:x2=2py(p>0)的通径长为,若抛物线C上有一动弦AB的中点为M,且弦AB的长度为3.
①求抛物线C的方程;
②求点M的纵坐标的最小值.
解析:(2)①由题意可知:2p=,所以抛物线C的方程为x2=y;
②由题意可知:直线AB斜率必存在,设其方程为y=kx+b.
设A(x1,y1),B(x2,y2),M(x0,y0).则x0=,y0=,
联立方程得2x2-kx-b=0.
所以,y1+y2=+2b.
又知:|AB|=
= =3,
得2b=,
∴y0==+2b)=)
=)≥(2)=.
当且仅当=,即k2=5时取等号,
则点M的纵坐标的最小值为.
题型二 范围问题
例2 [2023·广东揭阳期末]已知椭圆C:=1(a>b>0)的离心率为,点A()在椭圆C上.
(1)求椭圆C的标准方程;
(2)已知直线l:y=k(x-3)(k≠0)与椭圆C交于P,Q两点,点M是线段PQ的中点,直线l′过点M,且与直线l垂直.记直线l′与y轴的交点为N,求|MN|的取值范围.
解析:(1)由题意可得,解得a2=4,b2=3.
故椭圆C的标准方程为=1.
(2)设P(x1,y1),Q(x2,y2),M(x0,y0).
联立,整理得(4k2+3)x2-24k2x+36k2-12=0,
则Δ=(-24k2)2-4(4k2+3)(36k2-12)=48(3-5k2)>0,解得0
因为M是线段PQ的中点,所以x0==,
则y0=k(x0-3)=-,故M(,-).
直线l′的方程为y-y0=-(x-x0),即y+=-(x-).
令x=0,得y=-(0-)-=,
则N(0,),
所以|MN|==.
设t=4k2+3,则k2=,
故|MN|==3=3.
因为0
解圆锥曲线中范围问题的策略
巩固训练2
(1)[2023·辽宁抚顺期末]已知椭圆C1的方程为=1,双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点.
(ⅰ)求双曲线C2的方程;
(ⅱ)若直线l:y=kx+2与双曲线C2恒有两个不同的交点A和B,且·>1(其中O为原点),求k的取值范围.
解析:(1)ⅰ由题,在椭圆C1中,焦点坐标为(-1,0)和(1,0);左右顶点为(-2,0)和(2,0),
因为双曲线C2的左、右焦点分别为C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点,
所以在双曲线C2中,设双曲线方程为=1,则a2=1,c2=4,所以b2=c2-a2=3,
所以双曲线C2的方程为x2-=1.
ⅱ由ⅰ联立,消去y,得(k2-3)x2+4kx+7=0;①
消去x,得(k2-3)y2+12y-12+3k2=0.②
设A(x1,y1),B(x2,y2),则x1,x2为方程①的两根,y1,y2为方程②的两根;
x1·x2=,y1·y2=,
·=x1·x2+y1·y2=>1,
得k2>3或k2<1,③
又因为方程①中,Δ=16k2-4×7(k2-3)=-12k2+84>0,得k2<7,④
③④联立得k的取值范围(-,-)∪(-1,1)∪(, ).
(2)[2023·湖北武汉模拟]已知动圆C过定点A(2,0),且在y轴上截得的弦长为4,圆心C的轨迹为曲线Γ.
(ⅰ)求Γ的方程;
(ⅱ)过点P(1,0)的直线l与Γ相交于M,N两点.设=λ,若λ∈[2,3],求l在y轴上截距的取值范围.
解析:(2)ⅰ设C(x,y),圆C的半径为R,则R2=22+x2=(x-2)2+(y-0)2整理,得y2=4x,所以Γ的方程为y2=4x.
ⅱ设M(x1,y1),N(x2,y2),又P(1,0),由=λ,得(x2-1,y2)=λ(1-x1,-y1)∴.由②,得==4x2∴x2=λ2x1③,联立①、③解得x2=λ,依题意有λ>0,∴N(λ,2)或N(λ,-2),又P(1,0),∴直线l的方程为(λ-1)y=2(x-1),或(λ-1)y=-2(x-1),当λ∈[2,3]时,l在y轴上的截距为或-,由=,可知在[2,3]上是单调递减的,∴≤2,-2≤-≤-,∴直线l在y轴上截距的取值范围为[-2,-∪,2].
真题展台
1.[2021·全国乙卷]已知抛物线C:y2=2px(p>0)的焦点F到准线的距离为2.
(1)求C的方程;
(2)已知O为坐标原点,点P在C上,点Q满足=9,求直线OQ斜率的最大值.
解析:(1)抛物线C:y2=2px(p>0)的焦点F(,0),准线方程为x=-,
由题意,该抛物线焦点到准线的距离为-(-)=p=2,
所以该抛物线的方程为y2=4x.
(2)设Q(x0,y0),则=9=(9-9x0,-9y0),
所以P(10x0-9,10y0),
由P在抛物线上可得(10y0)2=4(10x0-9),即x0=,
所以直线OQ的斜率kOQ===,
当y0=0时,kOQ=0;
当y0≠0时,kOQ=,当y0>0时,因为25y0+≥2=30,此时0
2.[2021·北京卷]已知椭圆E:=1(a>b>0)过点A(0,-2),以四个顶点围成的四边形面积为4.
(1)求椭圆E的标准方程;
(2)过点P(0,-3)的直线l斜率为k,交椭圆E于不同的两点B,C,直线AB,AC交y=-3于点M、N,若|PM|+|PN|≤15,求k的取值范围.
解析:(1)因为椭圆过A(0,-2),故b=2,
因为四个顶点围成的四边形的面积为4,故×2a×2b=4,即a=,
故椭圆的标准方程为=1.
(2)设B(x1,y1),C(x2,y2),
因为直线BC的斜率存在,故x1x2≠0,
故直线AB:y=x-2,令y=-3,
则xM=-,同理xN=-.
直线BC:y=kx-3,由可得(4+5k2)x2-30kx+25=0,
故Δ=900k2-100(4+5k2)>0,解得k<-1或k>1.
又x1+x2=,x1x2=,故x1x2>0,所以xMxN>0.
又|PM|+|PN|=|xM+xN|=||
=||=||=||=5|k|,
故5|k|≤15即|k|≤3,
综上,-3≤k<-1或1
(1)求C的方程;
(2)点N为椭圆上任意一点,求△AMN的面积的最大值.
解析:(1)由题意可知直线AM的方程为y-3=(x-2),即x-2y=-4.
当y=0时,解得x=-4,所以a=4.
椭圆C:=1(a>b>0)过点M(2,3),可得=1,解得b2=12.
所以C的方程:=1.
(2)设与直线AM平行的直线方程为x-2y=m,
如图所示,当直线与椭圆相切时,与AM距离比较远的直线与椭圆的切点为N,此时△AMN的面积取得最大值.
联立直线方程x-2y=m与椭圆方程=1,
可得3(m+2y)2+4y2=48,
化简可得16y2+12my+3m2-48=0,
所以Δ=144m2-4×16(3m2-48)=0,
即m2=64,解得m=±8,
与AM距离比较远的直线方程:x-2y=8,
直线AM方程为x-2y=-4,
点N到直线AM的距离即两平行线之间的距离,
利用平行线之间的距离公式可得d==,
由两点之间距离公式可得|AM|==3.
所以△AMN的面积的最大值为×3=18.
同课章节目录
