2023届考前小题专攻 专题七 函数与导数 第二讲 导数 课件(共36张)
文档属性
| 名称 | 2023届考前小题专攻 专题七 函数与导数 第二讲 导数 课件(共36张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-19 15:57:14 | ||
图片预览








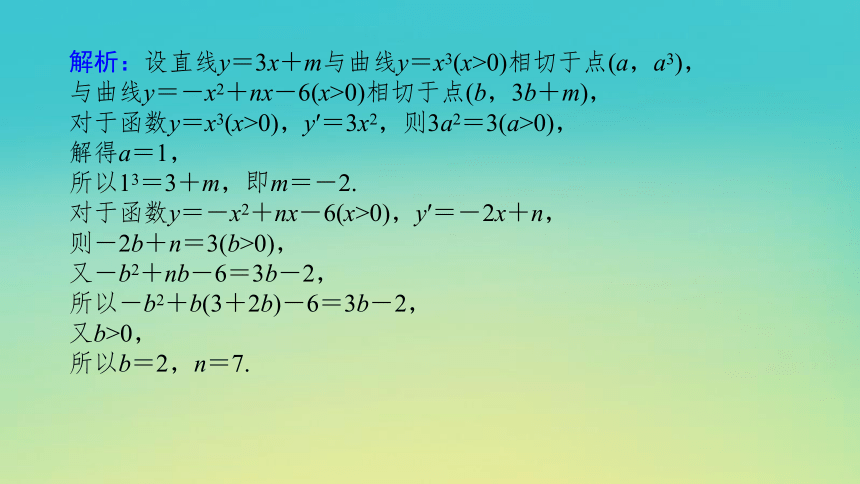



文档简介
(共36张PPT)
第二讲 导数
微专题1
微专题2
微专题3
微专题1
常考常用结论
1.函数y=f(x)在点x=x0处的导数的几何意义,就是曲线在点P(x0,f(x0))处的切线的斜率.用好这个条件是解决切线问题的关键.
2.曲线y=f(x)在点P(x0,y0)处的切线是指P为切点,斜率为k=f′(x0)的切线,是唯一的一条切线.
3.曲线y=f(x)过点P(x0,y0)的切线是指切线经过点P,点P可以是切点,也可以不是切点,而且这样的直线可能有多条.
保分题
1.[2022·广东广州一模]曲线y=x3+1在点(-1,a)处的切线方程为( )
A.y=3x+3 B.y=3x+1
C.y=-3x-1 D.y=-3x-3
答案:A
解析:∵y=f(x)=x3+1,
∴f′(x)=3x2,所以f′(-1)=3,
又当x=-1时,a=(-1)3+1=-1+1=0,
所以y=x3+1在点(-1,a)处的切线方程为:y=3(x+1),即y=3x+3.
2.[2022·山东枣庄三模]曲线y=x3+bx2+c在点M(1,0)处的切线与直线x-y-2=0垂直,则c的值为( )
A.-1 B.0
C.1 D.2
答案:C
解析:设f(x)=x3+bx2+c,则f′(x)=3x2+2bx,直线x-y-2=0的斜率为1,
由题意可得解得.
3.[2022·河北沧州二模]若直线x-y-b=0是曲线y=2的一条切线,则实数b=________.
-1
解析:因为y=2,所以y′=,令=1,得x=1,
所以切点为,代入x-y-b=0,得b=-1.
提分题
例1 (1)[2022·河北保定二模](多选)若直线y=3x+m是曲线y=x3(x>0)与曲线y=+nx-6(x>0)的公切线,则( )
A.m=-2 B.m=-1
C.n=6 D.n=7
答案:AD
解析:设直线y=3x+m与曲线y=x3(x>0)相切于点(a,a3),
与曲线y=-x2+nx-6(x>0)相切于点(b,3b+m),
对于函数y=x3(x>0),y′=3x2,则3a2=3(a>0),
解得a=1,
所以13=3+m,即m=-2.
对于函数y=-x2+nx-6(x>0),y′=-2x+n,
则-2b+n=3(b>0),
又-b2+nb-6=3b-2,
所以-b2+b(3+2b)-6=3b-2,
又b>0,
所以b=2,n=7.
(2)[2022·新高考Ⅱ卷]曲线y=ln |x|过坐标原点的两条切线的方程为______,________.
y=
y=-
解析:当x>0时,y=ln x,y′=.假设此时直线与曲线y=ln x相切于点(x1,ln x1)(x1>0),则此时切线方程为=(x-x1).若该切线经过原点,则ln x1-1=0,解得x1=e,此时切线方程为y=.当x<0时,y=ln (-x),y′=.假设此时直线与曲线y=ln (-x)相切于点(x2,ln (-x2))(x2<0),则此时切线方程为y-ln (-x2)=(x-x2).若该切线经过原点,则ln (-x2)-1=0,解得x2=-e,此时切线方程为y=-.
技法领悟
解决此类问题通常有两种方法
1.利用其中一曲线在某点处的切线与另一曲线相切,列出关系式求解;
2.设公切线l在y=f(x)上的切点P1(x1,f(x1)),在y=g(x)上的切点P2(x2,g(x2)),则f′(x1)=g′(x2)=.
巩固训练1
1.[2022·河北秦皇岛二模]已知函数f(x)为偶函数,当x>0时,f(x)=ln x-e1-x,则曲线y=f(x)在x=-1处的切线方程为( )
A.y-e2+1=0
B.y+1=0
C.(e2-1)x-y+e2-2=0
D.2x+y+3=0
答案:D
解析:因为f(x)为偶函数,设x<0,则-x>0,所以f(x)=f(-x)=ln (-x)-e1+x,所以f(-1)=-1.因为当x<0时,f′(x)=-e1+x,所以f′(-1)=-2,所以曲线y=f(x)在x=-1处的切线方程为y+1=-2(x+1),即2x+y+3=0.
2.[2022·湖南湘潭三模]已知直线l是曲线y=ex-1与y=ln x+1的公共切线,则l的方程为______________.
y=ex-1或y=x
解析:设l与曲线y=ex-1相切于点P(a,ea-1),与曲线y=ln x+1相切于点Q(b,ln b+1),
则ea==,整理得(a-1)(ea-1)=0,解得a=1或a=0,
当a=1时,l的方程为y=ex-1;当a=0时,l的方程为y=x.
微专题2
常考常用结论
1.f′(x)>0是f(x)为增函数的充分不必要条件,如函数f(x)=x3在(-∞,+∞)上单调递增,但f′(x)≥0.
2.f′(x)≥0是f(x)为增函数的必要不充分条件,当函数在某个区间内恒有f′(x)=0时,则f(x)为常数,函数不具有单调性.
保分题
1.[2022·山东德州二模]已知函数f(x)是偶函数,其导函数f′(x)的图象见下图,且f(x+2)=f(2-x)对x∈R恒成立,则下列说法正确的是( )
A.f(-1)<f()<f()
B.f<f<f
C.f(-1)<f<f
D.f<f(-1)<f
答案:D
解析:∵f(-x)=f(x), ∴f(-1)=f(1),
∵f(x+2)=f(2-x),∴f=f,
又由导函数的图象得,
当x∈(0,2)时,f′(x)>0,f(x)单调递增,
∴f∴f<f(-1)<f.
2.已知函数f(x)=x3-x2+2x+1在R上单週递增,则a=( )
A. B.0
C.- D.-1
答案:A
解析:f′(x)=ax2-(2a+1)x+2,
∵函数f(x)在R上单调递增,
∴f′(x)≥0在R上恒成立,
∴a>0,且Δ=(2a+1)2-8a≤0,解得a=.
3.已知定义在R上的函数f(x)的导函数f′(x)>1,且f(2m)(-∞,1)
解析:∵定义在R上的函数f(x)的导函数f′(x)>1>0,
∴f(x)在R上单调递增,
由f(2m)∴实数m的取值范围为(-∞,1).
提分题
例2 (1)[2022·福建南平三模]对任意的x1,x2∈(1,3],当x10恒成立,则实数a的取值范围是( )
A.[3,+∞) B.(3,+∞)
C.[9,+∞) D.(9,+∞)
答案:C
解析:x1-x2-ln >0,即x1-ln x1>x2-ln x2,
令f(x)=x-ln x,由题意得f(x)在(1,3]上单调递减,
故f′(x)=1-≤0,即a≥3x在(1,3]上恒成立,则a≥9.
(2)[2022·江苏无锡二模]已知a=ln ,b=e-1,c=(9-3ln 3)e-3,则a,b,c的大小为( )
A.aC.c答案:C
解析:令函数f(x)=(x≥e),当x>e时,求导得:f′(x)=<0,
则函数f(x)在[e,+∞)上单调递减,又a==f(3),b==f(e),c===f(),
显然e<3<,则有f所以c技法领悟
1.利用导数比较大小或解不等式的常见技巧
利用题目条件,构造辅助函数,把比较大小或解不等式的问题转化为先利用导数研究函数的单调性问题,再由单调性比较大小或解不等式.
2.由函数的单调性求参数取值范围的策略
(1)可导函数在区间(a,b)上单调,实际上就是在该区间上f′(x)≥0(或f′(x)≤0)恒成立,得到关于参数的不等式,从而转化为求函数的最值问题,求参数的取值范围;
(2)可导函数在区间(a,b)上存在单调区间,实际上就是f′(x)>0(或f′(x)<0)在该区间上存在解集,即f′(x)max>0(或f′(x)min<0)在该区间上有解,从而转化为不等式问题,求参数的取值范围.
巩固训练2
1.已知函数f(x)=(x-1)ex-kx3+1,若对任意的x1,x2∈(0,+∞),且x1≠x2,都有(x1-x2)[f(x1)-f(x2)]>0,则实数k的取值范围是( )
A. B.
C. D.
答案:B
解析:由(x1-x2)[f(x1)-f(x2)]>0可知:f(x)在(0,+∞)单调递增.
故f′(x)=xex-3kx2≥0 ex-3kx≥0 3k≤在(0,+∞)上恒成立,
记g(x)=(x>0),∴g′(x)=,当x∈(0,1)时,g′(x)<0,则g(x)单调递减,
当x∈(1,+∞)时,g′(x)>0,则g(x)单调递增,
所以g(x)在(0,+∞)上有最小值为g(1)=e,所以3k≤e k≤.
2.[2022·河北邯郸二模]已知函数f(x)=ln x,且a=f,b=f,c=f,则( )
A.a>b>c B.c>a>b
C.a>c>b D.c>b>a
答案:B
解析:由f(x)=ln x f′(x)=ln x(1+)+(1-),
当x∈(0,1)时,f′(x)<0,f(x)单调递减,
因为f()=f()=),所以c=f(),
因为0<<<<1,所以f()>f()>f(),故c>a>b.
微专题3
常考常用结论
1.函数f(x)在x0处的导数f′(x0)=0且f′(x)在x0附近“左正右负” f(x)在x0处取极大值;函数f(x)在x0处的导数f′(x0)=0且f′(x)在x0附近“左负右正” f(x)在x0处取极小值.
2.在闭区间[a,b]上的连续函数y=f(x),在[a,b]上必有最大值与最小值.在[a,b]上的连续函数y=f(x),若有唯一的极值点,则这个极值点就是最值点.
3.单调函数没有极值,如果一个函数没有极值,则该函数是单调函数或者常函数.
4.开区间内的单调函数没有极值.
保分题
1.已知函数f(x)=x2-8x+6ln x+1,则f(x)的极大值为( )
A.10 B.-6
C.-7 D.0
答案:B
解析:函数f(x)的定义域为(0,+∞),
f′(x)=2x-8+=,令f′(x)=0,解得x=1或x=3,
故
所以f(x)的极大值为f(1)=-6.
x (0,1) 1 (1,3) 3 (3,+∞)
f′(x) >0 =0 <0 =0 >0
f(x) 单调递增 极大值 单调递减 极小值 单调递增
2.[2022·全国甲卷]当x=1时,函数f(x)=a ln x+取得最大值-2,则f′(2)=( )
A.-1 B.-
C. D.1
答案:B
解析:由题意,得f(x)的定义域为(0,+∞),f′(x)==.又当x=1时,f(x)取得最大值-2,所以即所以a=b=-2,则f′(x)=,所以f′(2)==-.故选B.
3.若函数f(x)=x3-ax在x=3处有极小值,则实数a=________.
9
解析:因为f(x)=x3-ax,所以f′(x)=x2-a,
由32-a=0,得a=9.
当a=9时,f′(x)=x2-9=(x+3)(x-3),
所以函数f(x)在(-∞,-3),(3,+∞)单调递增,在(-3,3)单调递减.
函数在x=3处有极小值,满足题意.
提分题
例3 (1)已知函数f(x)=x3-ax2+x在区间上既有极大值又有极小值,则实数a的取值范围是( )
A.(2,+∞) B.[2,+∞)
C. D.
答案:C
解析:(1)函数f(x)=x3-ax2+x,导函数f′(x)=x2-ax+1.
因为f(x)在上既有极大值又有极小值,所以f′(x)=0在内应有两个不同的异号实数根.
,解得:2(2)[2022·湖北卓越高中联盟模拟]f(x)=|ln (ax)-2|+ax,f(x)的最小值为________.
3
解析:令ax=t∈(0,+∞),
则y=|ln t-2|+t=,
当t≥e2时,y=ln t+t-2单调递增,ymin=e2,
当00t>1时g′(t)>0,g(t)单调递增,
∴g(t)min=g(1)=3,
综上:f(x)min=3.
技法领悟
1.求函数极值时,不要误把极值点代入导函数中.
2.对于可导函数f(x),f′(x0)=0是函数f(x)在x=x0处有极值的必要不充分条件.
巩固训练3
1.若函数f(x)=x3-ax2-bx+a2在x=1处有极值10,则a-b=( )
A.6 B.-15
C.-6或15 D.6或-15
答案:B
解析:∵f(x)=x3-ax2-bx+a2,∴f′(x)=3x2-2ax-b,
又x=1 时f(x) 有极值10,
∴ ,解得 或,
当a=3,b=-3 时,f′(x)=3x2-6x+3=3(x-1)2≥0,
此时f(x) 在x=1 处无极值,不符合题意,
经检验,a=-4,b=11 时满足题意,
∴a-b=-15.
2.函数f(x)=|x-1|-ln x的最小值为________.
0
解析:函数f(x)=|x-1|-ln x的定义域为(0,+∞).
当0当x>1时,f(x)=|x-1|-ln x=x-1-ln x,
则f′(x)=1-=>0,所以f(x)在(1,+∞)上单调递增,
∵f(x)在(0,+∞)上是连续函数,
∴当x∈(0,1]时,f(x)单调递减,当x∈(1,+∞)时,f(x)单调递增.
∴当x=1时f(x)取得最小值为f(x)min=f(1)=|1-1|-ln 1=0.
第二讲 导数
微专题1
微专题2
微专题3
微专题1
常考常用结论
1.函数y=f(x)在点x=x0处的导数的几何意义,就是曲线在点P(x0,f(x0))处的切线的斜率.用好这个条件是解决切线问题的关键.
2.曲线y=f(x)在点P(x0,y0)处的切线是指P为切点,斜率为k=f′(x0)的切线,是唯一的一条切线.
3.曲线y=f(x)过点P(x0,y0)的切线是指切线经过点P,点P可以是切点,也可以不是切点,而且这样的直线可能有多条.
保分题
1.[2022·广东广州一模]曲线y=x3+1在点(-1,a)处的切线方程为( )
A.y=3x+3 B.y=3x+1
C.y=-3x-1 D.y=-3x-3
答案:A
解析:∵y=f(x)=x3+1,
∴f′(x)=3x2,所以f′(-1)=3,
又当x=-1时,a=(-1)3+1=-1+1=0,
所以y=x3+1在点(-1,a)处的切线方程为:y=3(x+1),即y=3x+3.
2.[2022·山东枣庄三模]曲线y=x3+bx2+c在点M(1,0)处的切线与直线x-y-2=0垂直,则c的值为( )
A.-1 B.0
C.1 D.2
答案:C
解析:设f(x)=x3+bx2+c,则f′(x)=3x2+2bx,直线x-y-2=0的斜率为1,
由题意可得解得.
3.[2022·河北沧州二模]若直线x-y-b=0是曲线y=2的一条切线,则实数b=________.
-1
解析:因为y=2,所以y′=,令=1,得x=1,
所以切点为,代入x-y-b=0,得b=-1.
提分题
例1 (1)[2022·河北保定二模](多选)若直线y=3x+m是曲线y=x3(x>0)与曲线y=+nx-6(x>0)的公切线,则( )
A.m=-2 B.m=-1
C.n=6 D.n=7
答案:AD
解析:设直线y=3x+m与曲线y=x3(x>0)相切于点(a,a3),
与曲线y=-x2+nx-6(x>0)相切于点(b,3b+m),
对于函数y=x3(x>0),y′=3x2,则3a2=3(a>0),
解得a=1,
所以13=3+m,即m=-2.
对于函数y=-x2+nx-6(x>0),y′=-2x+n,
则-2b+n=3(b>0),
又-b2+nb-6=3b-2,
所以-b2+b(3+2b)-6=3b-2,
又b>0,
所以b=2,n=7.
(2)[2022·新高考Ⅱ卷]曲线y=ln |x|过坐标原点的两条切线的方程为______,________.
y=
y=-
解析:当x>0时,y=ln x,y′=.假设此时直线与曲线y=ln x相切于点(x1,ln x1)(x1>0),则此时切线方程为=(x-x1).若该切线经过原点,则ln x1-1=0,解得x1=e,此时切线方程为y=.当x<0时,y=ln (-x),y′=.假设此时直线与曲线y=ln (-x)相切于点(x2,ln (-x2))(x2<0),则此时切线方程为y-ln (-x2)=(x-x2).若该切线经过原点,则ln (-x2)-1=0,解得x2=-e,此时切线方程为y=-.
技法领悟
解决此类问题通常有两种方法
1.利用其中一曲线在某点处的切线与另一曲线相切,列出关系式求解;
2.设公切线l在y=f(x)上的切点P1(x1,f(x1)),在y=g(x)上的切点P2(x2,g(x2)),则f′(x1)=g′(x2)=.
巩固训练1
1.[2022·河北秦皇岛二模]已知函数f(x)为偶函数,当x>0时,f(x)=ln x-e1-x,则曲线y=f(x)在x=-1处的切线方程为( )
A.y-e2+1=0
B.y+1=0
C.(e2-1)x-y+e2-2=0
D.2x+y+3=0
答案:D
解析:因为f(x)为偶函数,设x<0,则-x>0,所以f(x)=f(-x)=ln (-x)-e1+x,所以f(-1)=-1.因为当x<0时,f′(x)=-e1+x,所以f′(-1)=-2,所以曲线y=f(x)在x=-1处的切线方程为y+1=-2(x+1),即2x+y+3=0.
2.[2022·湖南湘潭三模]已知直线l是曲线y=ex-1与y=ln x+1的公共切线,则l的方程为______________.
y=ex-1或y=x
解析:设l与曲线y=ex-1相切于点P(a,ea-1),与曲线y=ln x+1相切于点Q(b,ln b+1),
则ea==,整理得(a-1)(ea-1)=0,解得a=1或a=0,
当a=1时,l的方程为y=ex-1;当a=0时,l的方程为y=x.
微专题2
常考常用结论
1.f′(x)>0是f(x)为增函数的充分不必要条件,如函数f(x)=x3在(-∞,+∞)上单调递增,但f′(x)≥0.
2.f′(x)≥0是f(x)为增函数的必要不充分条件,当函数在某个区间内恒有f′(x)=0时,则f(x)为常数,函数不具有单调性.
保分题
1.[2022·山东德州二模]已知函数f(x)是偶函数,其导函数f′(x)的图象见下图,且f(x+2)=f(2-x)对x∈R恒成立,则下列说法正确的是( )
A.f(-1)<f()<f()
B.f<f<f
C.f(-1)<f<f
D.f<f(-1)<f
答案:D
解析:∵f(-x)=f(x), ∴f(-1)=f(1),
∵f(x+2)=f(2-x),∴f=f,
又由导函数的图象得,
当x∈(0,2)时,f′(x)>0,f(x)单调递增,
∴f
2.已知函数f(x)=x3-x2+2x+1在R上单週递增,则a=( )
A. B.0
C.- D.-1
答案:A
解析:f′(x)=ax2-(2a+1)x+2,
∵函数f(x)在R上单调递增,
∴f′(x)≥0在R上恒成立,
∴a>0,且Δ=(2a+1)2-8a≤0,解得a=.
3.已知定义在R上的函数f(x)的导函数f′(x)>1,且f(2m)
解析:∵定义在R上的函数f(x)的导函数f′(x)>1>0,
∴f(x)在R上单调递增,
由f(2m)
提分题
例2 (1)[2022·福建南平三模]对任意的x1,x2∈(1,3],当x1
A.[3,+∞) B.(3,+∞)
C.[9,+∞) D.(9,+∞)
答案:C
解析:x1-x2-ln >0,即x1-ln x1>x2-ln x2,
令f(x)=x-ln x,由题意得f(x)在(1,3]上单调递减,
故f′(x)=1-≤0,即a≥3x在(1,3]上恒成立,则a≥9.
(2)[2022·江苏无锡二模]已知a=ln ,b=e-1,c=(9-3ln 3)e-3,则a,b,c的大小为( )
A.a
解析:令函数f(x)=(x≥e),当x>e时,求导得:f′(x)=<0,
则函数f(x)在[e,+∞)上单调递减,又a==f(3),b==f(e),c===f(),
显然e<3<,则有f
1.利用导数比较大小或解不等式的常见技巧
利用题目条件,构造辅助函数,把比较大小或解不等式的问题转化为先利用导数研究函数的单调性问题,再由单调性比较大小或解不等式.
2.由函数的单调性求参数取值范围的策略
(1)可导函数在区间(a,b)上单调,实际上就是在该区间上f′(x)≥0(或f′(x)≤0)恒成立,得到关于参数的不等式,从而转化为求函数的最值问题,求参数的取值范围;
(2)可导函数在区间(a,b)上存在单调区间,实际上就是f′(x)>0(或f′(x)<0)在该区间上存在解集,即f′(x)max>0(或f′(x)min<0)在该区间上有解,从而转化为不等式问题,求参数的取值范围.
巩固训练2
1.已知函数f(x)=(x-1)ex-kx3+1,若对任意的x1,x2∈(0,+∞),且x1≠x2,都有(x1-x2)[f(x1)-f(x2)]>0,则实数k的取值范围是( )
A. B.
C. D.
答案:B
解析:由(x1-x2)[f(x1)-f(x2)]>0可知:f(x)在(0,+∞)单调递增.
故f′(x)=xex-3kx2≥0 ex-3kx≥0 3k≤在(0,+∞)上恒成立,
记g(x)=(x>0),∴g′(x)=,当x∈(0,1)时,g′(x)<0,则g(x)单调递减,
当x∈(1,+∞)时,g′(x)>0,则g(x)单调递增,
所以g(x)在(0,+∞)上有最小值为g(1)=e,所以3k≤e k≤.
2.[2022·河北邯郸二模]已知函数f(x)=ln x,且a=f,b=f,c=f,则( )
A.a>b>c B.c>a>b
C.a>c>b D.c>b>a
答案:B
解析:由f(x)=ln x f′(x)=ln x(1+)+(1-),
当x∈(0,1)时,f′(x)<0,f(x)单调递减,
因为f()=f()=),所以c=f(),
因为0<<<<1,所以f()>f()>f(),故c>a>b.
微专题3
常考常用结论
1.函数f(x)在x0处的导数f′(x0)=0且f′(x)在x0附近“左正右负” f(x)在x0处取极大值;函数f(x)在x0处的导数f′(x0)=0且f′(x)在x0附近“左负右正” f(x)在x0处取极小值.
2.在闭区间[a,b]上的连续函数y=f(x),在[a,b]上必有最大值与最小值.在[a,b]上的连续函数y=f(x),若有唯一的极值点,则这个极值点就是最值点.
3.单调函数没有极值,如果一个函数没有极值,则该函数是单调函数或者常函数.
4.开区间内的单调函数没有极值.
保分题
1.已知函数f(x)=x2-8x+6ln x+1,则f(x)的极大值为( )
A.10 B.-6
C.-7 D.0
答案:B
解析:函数f(x)的定义域为(0,+∞),
f′(x)=2x-8+=,令f′(x)=0,解得x=1或x=3,
故
所以f(x)的极大值为f(1)=-6.
x (0,1) 1 (1,3) 3 (3,+∞)
f′(x) >0 =0 <0 =0 >0
f(x) 单调递增 极大值 单调递减 极小值 单调递增
2.[2022·全国甲卷]当x=1时,函数f(x)=a ln x+取得最大值-2,则f′(2)=( )
A.-1 B.-
C. D.1
答案:B
解析:由题意,得f(x)的定义域为(0,+∞),f′(x)==.又当x=1时,f(x)取得最大值-2,所以即所以a=b=-2,则f′(x)=,所以f′(2)==-.故选B.
3.若函数f(x)=x3-ax在x=3处有极小值,则实数a=________.
9
解析:因为f(x)=x3-ax,所以f′(x)=x2-a,
由32-a=0,得a=9.
当a=9时,f′(x)=x2-9=(x+3)(x-3),
所以函数f(x)在(-∞,-3),(3,+∞)单调递增,在(-3,3)单调递减.
函数在x=3处有极小值,满足题意.
提分题
例3 (1)已知函数f(x)=x3-ax2+x在区间上既有极大值又有极小值,则实数a的取值范围是( )
A.(2,+∞) B.[2,+∞)
C. D.
答案:C
解析:(1)函数f(x)=x3-ax2+x,导函数f′(x)=x2-ax+1.
因为f(x)在上既有极大值又有极小值,所以f′(x)=0在内应有两个不同的异号实数根.
,解得:2
3
解析:令ax=t∈(0,+∞),
则y=|ln t-2|+t=,
当t≥e2时,y=ln t+t-2单调递增,ymin=e2,
当0
∴g(t)min=g(1)=3,
综上:f(x)min=3.
技法领悟
1.求函数极值时,不要误把极值点代入导函数中.
2.对于可导函数f(x),f′(x0)=0是函数f(x)在x=x0处有极值的必要不充分条件.
巩固训练3
1.若函数f(x)=x3-ax2-bx+a2在x=1处有极值10,则a-b=( )
A.6 B.-15
C.-6或15 D.6或-15
答案:B
解析:∵f(x)=x3-ax2-bx+a2,∴f′(x)=3x2-2ax-b,
又x=1 时f(x) 有极值10,
∴ ,解得 或,
当a=3,b=-3 时,f′(x)=3x2-6x+3=3(x-1)2≥0,
此时f(x) 在x=1 处无极值,不符合题意,
经检验,a=-4,b=11 时满足题意,
∴a-b=-15.
2.函数f(x)=|x-1|-ln x的最小值为________.
0
解析:函数f(x)=|x-1|-ln x的定义域为(0,+∞).
当0
则f′(x)=1-=>0,所以f(x)在(1,+∞)上单调递增,
∵f(x)在(0,+∞)上是连续函数,
∴当x∈(0,1]时,f(x)单调递减,当x∈(1,+∞)时,f(x)单调递增.
∴当x=1时f(x)取得最小值为f(x)min=f(1)=|1-1|-ln 1=0.
同课章节目录
