2023届考前小题专攻 专题七 函数与导数 第三讲 函数与导数 课件(共53张)
文档属性
| 名称 | 2023届考前小题专攻 专题七 函数与导数 第三讲 函数与导数 课件(共53张) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-19 15:58:58 | ||
图片预览





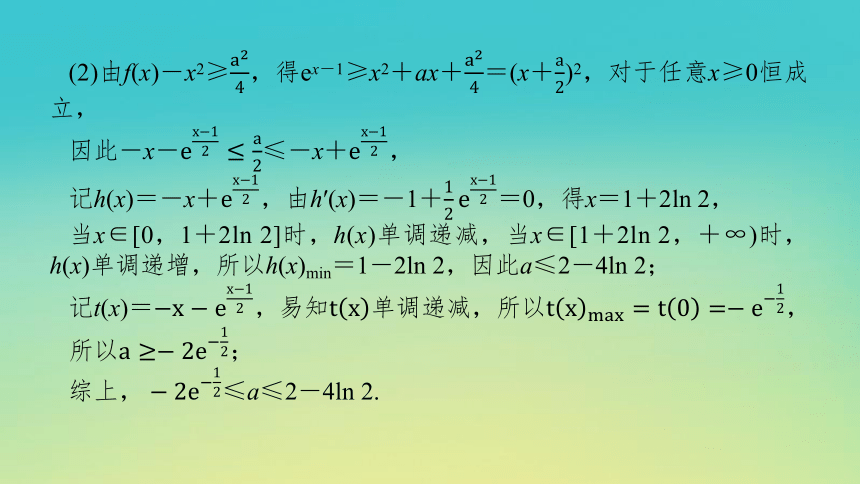

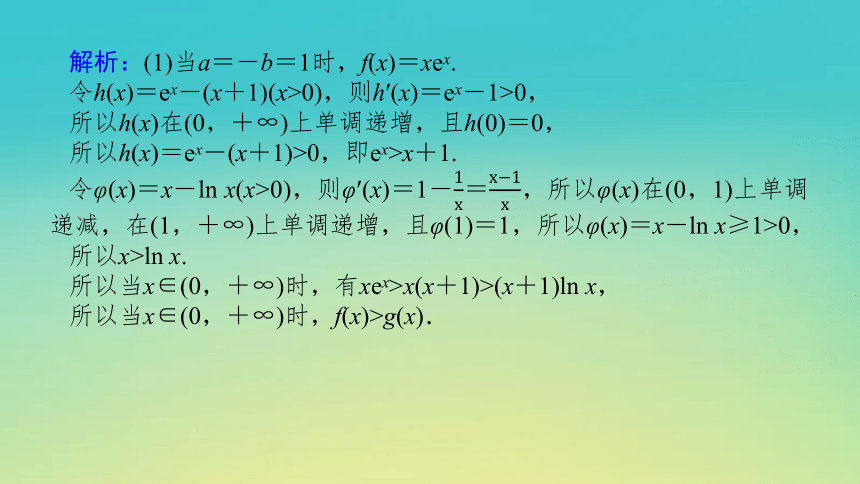




文档简介
(共53张PPT)
第三讲 函数与导数
微专题1
微专题2
微专题3
微专题1
提分题
例1 [2022·山东菏泽一模]已知函数f(x)=ex-1-ax.
(1)讨论f(x)的单调性;
(2)若f(x)-x2≥对于任意x≥0恒成立,求实数a的取值范围.
解析:(1)f′(x)=ex-1-a.
①当a≤0时,f′(x)>0,f(x)在(-∞,+∞)上单调递增;
②当a>0时,令f′(x)=ex-1-a=0,x=1+ln a,
当x∈(-∞,1+ln a)时,f′(x)<0,f(x)在(-∞,1+ln a)上单调递减;
当x∈(1+ln a,+∞)时,f′(x)>0,f(x)在(1+ln a,+∞)上单调递增;
(2)由f(x)-x2≥,得ex-1≥x2+ax+=(x+)2,对于任意x≥0恒成立,
因此-x-≤-x+,
记h(x)=-x+,由h′(x)=-1+=0,得x=1+2ln 2,
当x∈[0,1+2ln 2]时,h(x)单调递减,当x∈[1+2ln 2,+∞)时,h(x)单调递增,所以h(x)min=1-2ln 2,因此a≤2-4ln 2;
记t(x)=,
所以;
综上≤a≤2-4ln 2.
例2 [2022·河北张家口一模]已知函数f(x)=axeax+(a+b)x,g(x)=(1+x)ln x.
(1)当a=-b=1时,证明:当x∈(0,+∞)时,f(x)>g(x);
(2)若对 x∈(0,+∞),都 b∈[-1,0],使f(x)≥g(x)恒成立,求实数a的取值范围.
解析:(1)当a=-b=1时,f(x)=xex.
令h(x)=ex-(x+1)(x>0),则h′(x)=ex-1>0,
所以h(x)在(0,+∞)上单调递增,且h(0)=0,
所以h(x)=ex-(x+1)>0,即ex>x+1.
令φ(x)=x-ln x(x>0),则φ′(x)=1-=,所以φ(x)在(0,1)上单调递减,在(1,+∞)上单调递增,且φ(1)=1,所以φ(x)=x-ln x≥1>0,
所以x>ln x.
所以当x∈(0,+∞)时,有xex>x(x+1)>(x+1)ln x,
所以当x∈(0,+∞)时,f(x)>g(x).
(2)因为 b∈[-1,0],使f(x)≥g(x)恒成立,令φ(b)=axeax+(a+b)x,
只需φ(b)max≥g(x),即axeax+ax≥(1+x)ln x在x∈(0,+∞)上恒成立,
整理得ax(eax+1)≥(x+1)ln x=ln x(eln x+1).(*).
设F(x)=x(ex+1),则F′(x)=ex(x+1)+1,设H(x)=F′(x)=ex(x+1)+1,
又H′(x)=(x+2)ex,可得x>-2时,H′(x)>0,H(x)单调递增;x<-2时,H′(x)<0,H(x)单调递减,因此当x=-2时,H(x)有最小值H(-2)=1->0,
所以F(x)在R上单调递增.
所以(*)式即F(ax)≥F(ln x),所以ax≥ln x,即a≥.
设G(x)=,x>0,则G′(x)=,令G′(x)=0,解得x=e.
当00,函数G(x)单调递增;当x>e时,G′(x)<0,函数G(x)单调递减.
所以G(x)max =G(e)=,所以a≥.
所以实数a的取值范围为.
技法领悟
不等式恒成立(能成立)问题的解题策略
1.对于含参数的不等式,如果易分离参数,可先分离参数、构造函数,直接转化为求函数的最值;否则应进行分类讨论,在解题过程中,必要时,可作出函数图象草图,借助几何图形直观分析转化.
2.“恒成立”与“能成立”问题的求解是“互补”关系,即f(x)≥g(a)对于x∈D恒成立,应求f(x)的最小值;若存在x∈D,使得f(x)≥g(a)成立,应求f(x)的最大值.应特别关注等号是否取到,注意端点的取舍.
巩固训练1
1.已知函数f(x)=x ln x+ax+2.
(1)当a=0时,求f(x)的极值;
(2)若对任意的x∈[1,e2],f(x)≤0恒成立,求实数a的取值范围.
解析:(1)当a=0时,f(x)=x ln x+2,f(x)的定义域为(0,+∞),
f′(x)=ln x+1=0,则x=.
令f′(x)>0,则x∈(,+∞),令f′(x)<0,则x∈,
所以f(x)在上单调递减,在上单调递增.
当x=时,f(x)取得极小值且为f=ln +2=-+2,无极大值.
(2)f(x)=x ln x+ax+2≤0对任意的x∈恒成立,
则-a≥=+ln x对任意的x∈[1,e2]恒成立,
令g(x)=+ln x,g′(x)=-==0,所以x=2,
则g(x)在[1,2)上单调递减,在(2,e2]上单调递增,所以g(1)=2,g(e2)=+2,所以g(x)max=g(e2)=+2,则-a≥+2,则a≤--2.
实数a的取值范围为.
2.已知函数f(x)=x ln x,g(x)=-x2+ax-3(a∈R).
(1)求函数f(x)的单调递增区间;
(2)若对任意x∈(0,+∞),不等式f(x)≥g(x)恒成立,求a的取值范围.
解析:(1)f(x)=x ln x定义域为(0,+∞),f′(x)=ln x+1,
f′(x)>0即ln x+1>0,解得x>,
所以f(x)在(,+∞)单调递增.
(2)对任意x∈(0,+∞),不等式f(x)≥g(x)恒成立,即x ln x≥(-x2+ax-3)恒成立,
分离参数得a≤2ln x+x+.
令h(x)=2ln x+x+(x∈(0,+∞)),则h′(x)=.
当x∈(0,1)时,h′(x)<0,h(x)在(0,1)上单调递减;
当x∈(1,+∞)时,h′(x)>0,h(x)在(1,+∞)上单调递增.
所以h(x)min=h(1)=4,即a≤4,
故a的取值范围是(-∞,4].
微专题2
提分题
例3 [2022·广东汕头三模]已知函数f(x)=x-2sin x.
(1)求f(x)在(0,π)的极值;
(2)证明:函数g(x)=ln x-f(x)在(0,π)有且只有两个零点.
解析:(1)由f(x)=x-2sin x得f′(x)=1-2cos x,x∈(0,π),
令f′(x)=0得,x=,
当0当0,此时函数f(x)单调递增,
所以,函数f(x)的极小值为f=,无极大值.
(2)证明:g(x)=ln x-f(x)=ln x-x+2sin x,x∈(0,π),则g′(x)=-1+2cos x,
令φ(x)=+2cos x-1,则φ′(x)=--2sin x.
当x∈(0,π)时,φ′(x)=--2sin x<0,则φ(x)在(0,π)上单调递减,
∵φ=>0,φ=-1<0,
所以,存在x0∈,使得φ(x0)=g′(x0)=0.
当x变化时,g(x),g′(x)变化如表:
x (0,x0) x0 (x0,π)
g′(x) + 0 -
g(x) 单调递增 极大值g(x0) 单调递减
而g=ln >0,g(π)=ln π-π则g(x0)>g>0,又g=ln +1,
令h(x)=ln x-x+1,其中0则h′(x)=-1=>0,所以,函数h(x)在(0,1)上单调递增,
则h(x)由零点存在定理可知,函数g(x)在(0,π)上有两个零点.
例4 [2022·河北邯郸二模]已知函数f(x)=-a ln x,a≠0.
(1)若a=,分析f(x)的单调性;
(2)若f(x)在区间(1,e)上有零点,求实数a的取值范围.
解析:(1)x>0且f′(x)=,
设m(x)=ex-1-x m′(x)=ex-1-1,当x>1时,m′(x)>0,m(x)单调递增,
当x<1时,m′(x)<0,m(x)单调递减,故当x=1时,函数m(x)有最小值m(1)=0,
因此有m(x)=ex-1-x≥0 ex-1≥x,
设g(x)=2x2-x3-ex-1≤2x2-x3-x,
∴x>0时,2x2-x3-x=-x(x2-2x+1)=-x(x-1)2≤0,
∴g(x)≤0,即f′(x)≤0(取等号的条件是x=1),
f(x)是(0,+∞)上的单调递减函数;
(2)f(x)=0 h(x)==a在区间(1,e)上能成立,
h′(x)=且>0,
设n(x)=ln x-x+1 m′(x)=,当x>1时,n′(x)<0,n(x)单调递减,
当00,n(x)单调递增,故当x=1时,函数n(x)有最大值m(1)=0,
因此有n(x)=ln x-x+1≤0 ln x≤x-1,
设j(x)=2ln x-x ln x-1,则j(x)≤2(x-1)-x ln x-1=2x-x ln x-3,
设k(x)=2x-x ln x-3,则在区间(1,e)上k′(x)=1-ln x>0,k(x)单调递增,k(x)故j(x)≤k(x)在区间(1,e)上h(x)值域为(h(e),+∞)=(e2-e,+∞),
实数a的取值范围是(e2-e,+∞).
技法领悟
1.函数零点个数问题的解题策略
(1)直接法:直接研究函数,求出极值以及最值,画出草图.函数零点的个数问题即是函数图象与x轴交点的个数问题.
(2)分离参数法:分离出参数,转化为a=g(x),根据导数的知识求出函数g(x)在某区间的单调性,求出极值以及最值,画出草图.函数零点的个数问题即是直线y=a与函数y=g(x)图象交点的个数问题.只需要用a与函数g(x)的极值和最值进行比较即可.
2.根据函数零点的个数求参数范围的方法
(1)分离参数(a=g(x))后,将原问题转化为y=g(x)的值域(最值)问题或转化为直线y=a与y=g(x)的图象的交点个数问题(优选分离、次选分类)求解;
(2)利用零点的存在性定理构建不等式求解;
(3)转化为两个熟悉的函数图象的位置关系问题,从而构建不等式求解.
巩固训练2
1.已知函数f(x)=x-a ln x.
(1)当a=1时,求f(x)在区间(0,e]上的最小值;
(2)若f(x)有两个零点,求a的取值范围.
解析:(1) f′(x)=1-,令f′(x)=0,得x=1.当x∈(0,1)时,f′(x)<0,函数f(x)单调递减;当x∈(1,e]时,f′(x)>0,函数f(x)单调递增.
∴当x=1时,f(x)有极小值,也是最小值,最小值为f(1)=1.
(2)f(x)=x-a ln x=0,定义域x∈(0,+∞),由题意a≠0,
即=有两个零点,
令g(x)=,g′(x)=,
所以g(x)=在x∈(0,e)时,g′(x)>0,函数单调递增;当x∈(e,+∞)时,g′(x)<0,函数单调递减.
所以函数g(x)的最大值g(e)=,∵g(1)=0,x>e时,g(x)>0,
函数g(x)的图象如图所示,
所以0<<,所以a>e.
2.[2022·河北唐山二模]已知函数f(x)=,g(x)=b sin x,曲线y=f(x)和y=g(x)在原点处有相同的切线l.
(1)求b的值以及l的方程;
(2)判断函数h(x)=f(x)-g(x)在(0,+∞)上零点的个数,并说明理由.
解析:(1)依题意得:f′(x)= ,g′(x)=b cos x.
∴f′(0)=g′(0)=b=1,
∴b=1,l的方程:y=x.
(2)当x>时,=3->1≥sin x,h(x)>0,此时h(x)无零点.
当0令H(x)=-cos x,x∈,
则H′(x)=-+sin x,显然H′(x)在上单调递增,
又H′(0)=-<0,H′>0,所以存在t∈使得H′(t)=0,
因此可得0t0,H(x)单调递增;又H(0)=0,H>0,
所以存在λ∈,使得H(λ)=0,
即0λ0,h′(x)>0,h(x)单调递增;
又h(0)=0,h>0,所以h(x)在上有一个零点.
综上,h(x)在(0,+∞)上有1个零点.
微专题3
提分题
例5 [2022·河北沧州二模]已知函数f(x)=,a∈R.
(1)求f(x)的单调区间;
(2)证明:xf(x)+e-x>-a.
解析:(1)函数f(x)==ln x-,定义域为(0,+∞),f′(x)==,
①当a≥0时,f′(x)>0,f(x)单调递增;
②当a<0时,-a>0,x∈(0,-a)时,f′(x)<0,f(x)单调递减;
x∈(-a,+∞)时,f′(x)>0,f(x)单调递增,
综上,当a≥0时,f(x)的单调递增区间为(0,+∞),无单调递减区间;
当a<0时,f(x)的单调递减区间为(0,-a),单调递增区间为(-a,+∞).
(2)证明:由(1)知,当a=-1时,f(x)=ln x+,且f(x)≥f(1)=1,
所以x ln x+1≥x,
因为f(x)=,所以不等式xf(x)+e-x>-a等价于x ln x+e-x>0,
令g(x)=x+e-x-1,则g′(x)=1-e-x=>0在x>0时恒成立,
所以当x>0时,g(x)>g(0)=0,
又x ln x+1≥x,所以x ln x+e-x≥x-1+e-x>0,
故x ln x+e-x>0,即xf(x)+e-x>-a.
例6 [2022·山东省实验中学模拟]已知函数f(x)=.
(1)求函数y=f(x)的最大值;
(2)若关于x的方程ln x=xex-ex2+kx-1有实数根,求实数k的取值范围;
(3)证明:+…+<(n∈N*,n≥2).
解析:(1)f′(x)=,当x∈(0,1)时,f′(x)>0,当x∈(1,+∞)时,f′(x)<0,f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
所以f(x)max =f(1)=1,即当x=1时,f(x)取最大值1.
(2)依题意,ln x=xex-ex2+kx-1 k=+(ex-ex),令g(x)=+(ex-ex),g′(x)=+(e-ex),
当x∈(0,1)时,g′(x)>0,当x∈(1,+∞)时,g′(x)<0,g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
即g(x)max=g(1)=1,因此g(x)的值域是(-∞,1],方程k=+(ex-ex)有解,有k≤1,
所以实数k的取值范围是k≤1.
(3)证明:由(1)知f(x)≤1,当且仅当x=1时取等号,因此当x>1时,ln x即当n≥2时,ln n2所以+…+<[1-()+1-()+…+1-()]==.
例7 [2022·山东临沂一模]已知函数f(x)=ex-2a(a>0).
(1)若a=e,讨论f(x)的单调性;
(2)若x1,x2是函数f(x)的两个不同的零点,证明:1解析:(1)f(x)=ex-2a(a>0)的定义域为(0,+∞),f′(x)=ex-,
当a=e时,f′(x)=ex-,
令f′(x)=0,则x=1,
当01时,f′(x)>0,
所以f(x)在(0,1)上递减,在(1,+∞)上递增,
(2)因为x1,x2是函数f(x)的两个不同的零点,
所以==2a,
显然x1>0,x2>0,则有
x1=ln 2+ln a+ln x1,x2=ln 2+ln a+ln x2,
所以x1-x2=ln x1-ln x2,
不妨令x1>x2>0,设t=>1,
所以x1=,x2=,
所以要证x1+x2=>1,
只要证ln t>,即ln t->0,
令g(t)=ln t-(t>1),则g′(t)==>0,
所以g(t)在(1,+∞)上递增,
所以g(t)>g(1)=0,所以x1+x2>1,
因为x1=ln 2+ln a+ln x1,x2=ln 2+ln a+ln x2,
所以x1+x2=2ln 2+2ln a+ln (x1x2).
要证x1+x2<2ln a+ln 2,只要证ln (x1x2)<-ln 2,即x1x2<,
因为x1x2=,所以只要证<,
即ln t<,即ln t-<0,
令h(t)=ln t-,t>1,则h′(t)==-<0,
所以h(t)在(1,+∞)上递减,
所以h(t)综上,1技法领悟
1.证明单变量不等式的方法
(1)利用单调性证明单变量不等式
一般地,要证f(x)>g(x)在区间(a,b)上成立,需构造辅助函数F(x)=f(x)-g(x),通过分析F(x)在端点处的函数值来证明不等式.若F(a)=0,只需证明F(x)在(a,b)上单调递增即可;若F(b)=0,只需证明F(x)在(a,b)上单调递减即可.
(2)利用最值证明单变量不等式
利用最值证明单变量的不等式的常见形式是f(x)>g(x).证明技巧:先将不等式f(x)>g(x)移项,即构造函数h(x)=f(x)-g(x),转化为证不等式h(x)>0,再次转化为证明>0,因此,只需在所给的区间内,判断h′(x)的符号,从而判断其单调性,并求出函数h(x)的最小值,即可得证.
2.证明双变量函数不等式问题的策略
(1)将双变量中的一个看作变量,另一个看作常数,构造一个含参数的辅助函数证明不等式.
(2)整体换元.对于齐次式往往可将双变量整体换元,化为一元不等式.
(3)若双变量的函数不等式具有对称性,并且可以将两个变量分离开,分离之后的函数结构具有相似性,从而构造函数利用单调性证明.
巩固训练3
1.[2021·全国乙卷]设函数f(x)=ln (a-x),已知x=0是函数y=xf(x)的极值点.
(1)求a;
(2)设函数g(x)=,证明:g(x)<1.
解析:(1)由题意得y=xf(x)=x ln (a-x),
则y′=ln (a-x)+x[ln (a-x)]′.
因为x=0是函数y=xf(x)的极值点,
所以y′|x=0=ln a=0,所以a=1.
(2)证明:由(1)可知,f(x)=ln (1-x),其定义域为{x|x<1},
当0当x<0时,ln (1-x)>0,此时xf(x)<0.
易知g(x)的定义域为{x|x<1且x≠0},
故要证g(x)=<1,只需证x+f(x)>xf(x),即证x+ln (1-x)-x ln (1-x)>0.
令1-x=t,则t>0且t≠1,则只需证1-t+ln t-(1-t)ln t>0,即证1-t+t ln t>0.
令h(t)=1-t+t ln t,则h′(t)=-1+ln t+1=ln t,
所以h(t)在(0,1)上单调递减,在(1,+∞)上单调递增,所以h(t)>h(1)=0,
即g(x)<1成立.
2.[2022·河北张家口三模]已知函数g(x)=a ln x-(2a-2)x+x2(a∈R)在x=1处取得极值.
(1)求a的值及函数g(x)的极值;
(2)设f(x)=g(x)-t有三个不同的零点x1,x2,x3(x1解析:(1)函数g(x)的定义域为(0,+∞),g′(x)=,
由已知g′(1)=0,解得a=3,
∴g′(x)=,
∴当03时,g′(x)>0;当1∴g(x)在x=1处取得极大值g(1)=-,
在x=3处取得极小值g(3)=3ln 3-.
(2)证明:由(1)知g(x)=3ln x-4x+x2,极大值为g(1)=-,极小值为g(3)=3ln 3-,
由f(x)=g(x)-t有三个不同的零点x1,x2,x3,可知0设H(x)=g(x)-g(2-x),x∈(0,1),
∴H′(x)=g′(x)+g′(2-x)=>0,
∴H(x)在(0,1)上单调递增,H(x)∴g(x)由(1)知,g(x2)=g(x1)∴x2>2-x1,x1+x2>2 ①.
设h(x)=g(x)-g(6-x),x∈(1,3),
h′(x)=g′(x)+g′(6-x)=>0,∴h(x)在(1,3)上单调递增,
∴h(x)由(1)知g(x3)=g(x2)∴6-x2>x3 ②,
∴结合①②得x1+6>2+x3,
所以x3<4+x1.
第三讲 函数与导数
微专题1
微专题2
微专题3
微专题1
提分题
例1 [2022·山东菏泽一模]已知函数f(x)=ex-1-ax.
(1)讨论f(x)的单调性;
(2)若f(x)-x2≥对于任意x≥0恒成立,求实数a的取值范围.
解析:(1)f′(x)=ex-1-a.
①当a≤0时,f′(x)>0,f(x)在(-∞,+∞)上单调递增;
②当a>0时,令f′(x)=ex-1-a=0,x=1+ln a,
当x∈(-∞,1+ln a)时,f′(x)<0,f(x)在(-∞,1+ln a)上单调递减;
当x∈(1+ln a,+∞)时,f′(x)>0,f(x)在(1+ln a,+∞)上单调递增;
(2)由f(x)-x2≥,得ex-1≥x2+ax+=(x+)2,对于任意x≥0恒成立,
因此-x-≤-x+,
记h(x)=-x+,由h′(x)=-1+=0,得x=1+2ln 2,
当x∈[0,1+2ln 2]时,h(x)单调递减,当x∈[1+2ln 2,+∞)时,h(x)单调递增,所以h(x)min=1-2ln 2,因此a≤2-4ln 2;
记t(x)=,
所以;
综上≤a≤2-4ln 2.
例2 [2022·河北张家口一模]已知函数f(x)=axeax+(a+b)x,g(x)=(1+x)ln x.
(1)当a=-b=1时,证明:当x∈(0,+∞)时,f(x)>g(x);
(2)若对 x∈(0,+∞),都 b∈[-1,0],使f(x)≥g(x)恒成立,求实数a的取值范围.
解析:(1)当a=-b=1时,f(x)=xex.
令h(x)=ex-(x+1)(x>0),则h′(x)=ex-1>0,
所以h(x)在(0,+∞)上单调递增,且h(0)=0,
所以h(x)=ex-(x+1)>0,即ex>x+1.
令φ(x)=x-ln x(x>0),则φ′(x)=1-=,所以φ(x)在(0,1)上单调递减,在(1,+∞)上单调递增,且φ(1)=1,所以φ(x)=x-ln x≥1>0,
所以x>ln x.
所以当x∈(0,+∞)时,有xex>x(x+1)>(x+1)ln x,
所以当x∈(0,+∞)时,f(x)>g(x).
(2)因为 b∈[-1,0],使f(x)≥g(x)恒成立,令φ(b)=axeax+(a+b)x,
只需φ(b)max≥g(x),即axeax+ax≥(1+x)ln x在x∈(0,+∞)上恒成立,
整理得ax(eax+1)≥(x+1)ln x=ln x(eln x+1).(*).
设F(x)=x(ex+1),则F′(x)=ex(x+1)+1,设H(x)=F′(x)=ex(x+1)+1,
又H′(x)=(x+2)ex,可得x>-2时,H′(x)>0,H(x)单调递增;x<-2时,H′(x)<0,H(x)单调递减,因此当x=-2时,H(x)有最小值H(-2)=1->0,
所以F(x)在R上单调递增.
所以(*)式即F(ax)≥F(ln x),所以ax≥ln x,即a≥.
设G(x)=,x>0,则G′(x)=,令G′(x)=0,解得x=e.
当0
所以G(x)max =G(e)=,所以a≥.
所以实数a的取值范围为.
技法领悟
不等式恒成立(能成立)问题的解题策略
1.对于含参数的不等式,如果易分离参数,可先分离参数、构造函数,直接转化为求函数的最值;否则应进行分类讨论,在解题过程中,必要时,可作出函数图象草图,借助几何图形直观分析转化.
2.“恒成立”与“能成立”问题的求解是“互补”关系,即f(x)≥g(a)对于x∈D恒成立,应求f(x)的最小值;若存在x∈D,使得f(x)≥g(a)成立,应求f(x)的最大值.应特别关注等号是否取到,注意端点的取舍.
巩固训练1
1.已知函数f(x)=x ln x+ax+2.
(1)当a=0时,求f(x)的极值;
(2)若对任意的x∈[1,e2],f(x)≤0恒成立,求实数a的取值范围.
解析:(1)当a=0时,f(x)=x ln x+2,f(x)的定义域为(0,+∞),
f′(x)=ln x+1=0,则x=.
令f′(x)>0,则x∈(,+∞),令f′(x)<0,则x∈,
所以f(x)在上单调递减,在上单调递增.
当x=时,f(x)取得极小值且为f=ln +2=-+2,无极大值.
(2)f(x)=x ln x+ax+2≤0对任意的x∈恒成立,
则-a≥=+ln x对任意的x∈[1,e2]恒成立,
令g(x)=+ln x,g′(x)=-==0,所以x=2,
则g(x)在[1,2)上单调递减,在(2,e2]上单调递增,所以g(1)=2,g(e2)=+2,所以g(x)max=g(e2)=+2,则-a≥+2,则a≤--2.
实数a的取值范围为.
2.已知函数f(x)=x ln x,g(x)=-x2+ax-3(a∈R).
(1)求函数f(x)的单调递增区间;
(2)若对任意x∈(0,+∞),不等式f(x)≥g(x)恒成立,求a的取值范围.
解析:(1)f(x)=x ln x定义域为(0,+∞),f′(x)=ln x+1,
f′(x)>0即ln x+1>0,解得x>,
所以f(x)在(,+∞)单调递增.
(2)对任意x∈(0,+∞),不等式f(x)≥g(x)恒成立,即x ln x≥(-x2+ax-3)恒成立,
分离参数得a≤2ln x+x+.
令h(x)=2ln x+x+(x∈(0,+∞)),则h′(x)=.
当x∈(0,1)时,h′(x)<0,h(x)在(0,1)上单调递减;
当x∈(1,+∞)时,h′(x)>0,h(x)在(1,+∞)上单调递增.
所以h(x)min=h(1)=4,即a≤4,
故a的取值范围是(-∞,4].
微专题2
提分题
例3 [2022·广东汕头三模]已知函数f(x)=x-2sin x.
(1)求f(x)在(0,π)的极值;
(2)证明:函数g(x)=ln x-f(x)在(0,π)有且只有两个零点.
解析:(1)由f(x)=x-2sin x得f′(x)=1-2cos x,x∈(0,π),
令f′(x)=0得,x=,
当0
所以,函数f(x)的极小值为f=,无极大值.
(2)证明:g(x)=ln x-f(x)=ln x-x+2sin x,x∈(0,π),则g′(x)=-1+2cos x,
令φ(x)=+2cos x-1,则φ′(x)=--2sin x.
当x∈(0,π)时,φ′(x)=--2sin x<0,则φ(x)在(0,π)上单调递减,
∵φ=>0,φ=-1<0,
所以,存在x0∈,使得φ(x0)=g′(x0)=0.
当x变化时,g(x),g′(x)变化如表:
x (0,x0) x0 (x0,π)
g′(x) + 0 -
g(x) 单调递增 极大值g(x0) 单调递减
而g=ln >0,g(π)=ln π-π
令h(x)=ln x-x+1,其中0
则h(x)
例4 [2022·河北邯郸二模]已知函数f(x)=-a ln x,a≠0.
(1)若a=,分析f(x)的单调性;
(2)若f(x)在区间(1,e)上有零点,求实数a的取值范围.
解析:(1)x>0且f′(x)=,
设m(x)=ex-1-x m′(x)=ex-1-1,当x>1时,m′(x)>0,m(x)单调递增,
当x<1时,m′(x)<0,m(x)单调递减,故当x=1时,函数m(x)有最小值m(1)=0,
因此有m(x)=ex-1-x≥0 ex-1≥x,
设g(x)=2x2-x3-ex-1≤2x2-x3-x,
∴x>0时,2x2-x3-x=-x(x2-2x+1)=-x(x-1)2≤0,
∴g(x)≤0,即f′(x)≤0(取等号的条件是x=1),
f(x)是(0,+∞)上的单调递减函数;
(2)f(x)=0 h(x)==a在区间(1,e)上能成立,
h′(x)=且>0,
设n(x)=ln x-x+1 m′(x)=,当x>1时,n′(x)<0,n(x)单调递减,
当0
因此有n(x)=ln x-x+1≤0 ln x≤x-1,
设j(x)=2ln x-x ln x-1,则j(x)≤2(x-1)-x ln x-1=2x-x ln x-3,
设k(x)=2x-x ln x-3,则在区间(1,e)上k′(x)=1-ln x>0,k(x)单调递增,k(x)
实数a的取值范围是(e2-e,+∞).
技法领悟
1.函数零点个数问题的解题策略
(1)直接法:直接研究函数,求出极值以及最值,画出草图.函数零点的个数问题即是函数图象与x轴交点的个数问题.
(2)分离参数法:分离出参数,转化为a=g(x),根据导数的知识求出函数g(x)在某区间的单调性,求出极值以及最值,画出草图.函数零点的个数问题即是直线y=a与函数y=g(x)图象交点的个数问题.只需要用a与函数g(x)的极值和最值进行比较即可.
2.根据函数零点的个数求参数范围的方法
(1)分离参数(a=g(x))后,将原问题转化为y=g(x)的值域(最值)问题或转化为直线y=a与y=g(x)的图象的交点个数问题(优选分离、次选分类)求解;
(2)利用零点的存在性定理构建不等式求解;
(3)转化为两个熟悉的函数图象的位置关系问题,从而构建不等式求解.
巩固训练2
1.已知函数f(x)=x-a ln x.
(1)当a=1时,求f(x)在区间(0,e]上的最小值;
(2)若f(x)有两个零点,求a的取值范围.
解析:(1) f′(x)=1-,令f′(x)=0,得x=1.当x∈(0,1)时,f′(x)<0,函数f(x)单调递减;当x∈(1,e]时,f′(x)>0,函数f(x)单调递增.
∴当x=1时,f(x)有极小值,也是最小值,最小值为f(1)=1.
(2)f(x)=x-a ln x=0,定义域x∈(0,+∞),由题意a≠0,
即=有两个零点,
令g(x)=,g′(x)=,
所以g(x)=在x∈(0,e)时,g′(x)>0,函数单调递增;当x∈(e,+∞)时,g′(x)<0,函数单调递减.
所以函数g(x)的最大值g(e)=,∵g(1)=0,x>e时,g(x)>0,
函数g(x)的图象如图所示,
所以0<<,所以a>e.
2.[2022·河北唐山二模]已知函数f(x)=,g(x)=b sin x,曲线y=f(x)和y=g(x)在原点处有相同的切线l.
(1)求b的值以及l的方程;
(2)判断函数h(x)=f(x)-g(x)在(0,+∞)上零点的个数,并说明理由.
解析:(1)依题意得:f′(x)= ,g′(x)=b cos x.
∴f′(0)=g′(0)=b=1,
∴b=1,l的方程:y=x.
(2)当x>时,=3->1≥sin x,h(x)>0,此时h(x)无零点.
当0
则H′(x)=-+sin x,显然H′(x)在上单调递增,
又H′(0)=-<0,H′>0,所以存在t∈使得H′(t)=0,
因此可得0
所以存在λ∈,使得H(λ)=0,
即0
又h(0)=0,h>0,所以h(x)在上有一个零点.
综上,h(x)在(0,+∞)上有1个零点.
微专题3
提分题
例5 [2022·河北沧州二模]已知函数f(x)=,a∈R.
(1)求f(x)的单调区间;
(2)证明:xf(x)+e-x>-a.
解析:(1)函数f(x)==ln x-,定义域为(0,+∞),f′(x)==,
①当a≥0时,f′(x)>0,f(x)单调递增;
②当a<0时,-a>0,x∈(0,-a)时,f′(x)<0,f(x)单调递减;
x∈(-a,+∞)时,f′(x)>0,f(x)单调递增,
综上,当a≥0时,f(x)的单调递增区间为(0,+∞),无单调递减区间;
当a<0时,f(x)的单调递减区间为(0,-a),单调递增区间为(-a,+∞).
(2)证明:由(1)知,当a=-1时,f(x)=ln x+,且f(x)≥f(1)=1,
所以x ln x+1≥x,
因为f(x)=,所以不等式xf(x)+e-x>-a等价于x ln x+e-x>0,
令g(x)=x+e-x-1,则g′(x)=1-e-x=>0在x>0时恒成立,
所以当x>0时,g(x)>g(0)=0,
又x ln x+1≥x,所以x ln x+e-x≥x-1+e-x>0,
故x ln x+e-x>0,即xf(x)+e-x>-a.
例6 [2022·山东省实验中学模拟]已知函数f(x)=.
(1)求函数y=f(x)的最大值;
(2)若关于x的方程ln x=xex-ex2+kx-1有实数根,求实数k的取值范围;
(3)证明:+…+<(n∈N*,n≥2).
解析:(1)f′(x)=,当x∈(0,1)时,f′(x)>0,当x∈(1,+∞)时,f′(x)<0,f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
所以f(x)max =f(1)=1,即当x=1时,f(x)取最大值1.
(2)依题意,ln x=xex-ex2+kx-1 k=+(ex-ex),令g(x)=+(ex-ex),g′(x)=+(e-ex),
当x∈(0,1)时,g′(x)>0,当x∈(1,+∞)时,g′(x)<0,g(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
即g(x)max=g(1)=1,因此g(x)的值域是(-∞,1],方程k=+(ex-ex)有解,有k≤1,
所以实数k的取值范围是k≤1.
(3)证明:由(1)知f(x)≤1,当且仅当x=1时取等号,因此当x>1时,ln x
例7 [2022·山东临沂一模]已知函数f(x)=ex-2a(a>0).
(1)若a=e,讨论f(x)的单调性;
(2)若x1,x2是函数f(x)的两个不同的零点,证明:1
当a=e时,f′(x)=ex-,
令f′(x)=0,则x=1,
当0
所以f(x)在(0,1)上递减,在(1,+∞)上递增,
(2)因为x1,x2是函数f(x)的两个不同的零点,
所以==2a,
显然x1>0,x2>0,则有
x1=ln 2+ln a+ln x1,x2=ln 2+ln a+ln x2,
所以x1-x2=ln x1-ln x2,
不妨令x1>x2>0,设t=>1,
所以x1=,x2=,
所以要证x1+x2=>1,
只要证ln t>,即ln t->0,
令g(t)=ln t-(t>1),则g′(t)==>0,
所以g(t)在(1,+∞)上递增,
所以g(t)>g(1)=0,所以x1+x2>1,
因为x1=ln 2+ln a+ln x1,x2=ln 2+ln a+ln x2,
所以x1+x2=2ln 2+2ln a+ln (x1x2).
要证x1+x2<2ln a+ln 2,只要证ln (x1x2)<-ln 2,即x1x2<,
因为x1x2=,所以只要证<,
即ln t<,即ln t-<0,
令h(t)=ln t-,t>1,则h′(t)==-<0,
所以h(t)在(1,+∞)上递减,
所以h(t)
1.证明单变量不等式的方法
(1)利用单调性证明单变量不等式
一般地,要证f(x)>g(x)在区间(a,b)上成立,需构造辅助函数F(x)=f(x)-g(x),通过分析F(x)在端点处的函数值来证明不等式.若F(a)=0,只需证明F(x)在(a,b)上单调递增即可;若F(b)=0,只需证明F(x)在(a,b)上单调递减即可.
(2)利用最值证明单变量不等式
利用最值证明单变量的不等式的常见形式是f(x)>g(x).证明技巧:先将不等式f(x)>g(x)移项,即构造函数h(x)=f(x)-g(x),转化为证不等式h(x)>0,再次转化为证明>0,因此,只需在所给的区间内,判断h′(x)的符号,从而判断其单调性,并求出函数h(x)的最小值,即可得证.
2.证明双变量函数不等式问题的策略
(1)将双变量中的一个看作变量,另一个看作常数,构造一个含参数的辅助函数证明不等式.
(2)整体换元.对于齐次式往往可将双变量整体换元,化为一元不等式.
(3)若双变量的函数不等式具有对称性,并且可以将两个变量分离开,分离之后的函数结构具有相似性,从而构造函数利用单调性证明.
巩固训练3
1.[2021·全国乙卷]设函数f(x)=ln (a-x),已知x=0是函数y=xf(x)的极值点.
(1)求a;
(2)设函数g(x)=,证明:g(x)<1.
解析:(1)由题意得y=xf(x)=x ln (a-x),
则y′=ln (a-x)+x[ln (a-x)]′.
因为x=0是函数y=xf(x)的极值点,
所以y′|x=0=ln a=0,所以a=1.
(2)证明:由(1)可知,f(x)=ln (1-x),其定义域为{x|x<1},
当0
易知g(x)的定义域为{x|x<1且x≠0},
故要证g(x)=<1,只需证x+f(x)>xf(x),即证x+ln (1-x)-x ln (1-x)>0.
令1-x=t,则t>0且t≠1,则只需证1-t+ln t-(1-t)ln t>0,即证1-t+t ln t>0.
令h(t)=1-t+t ln t,则h′(t)=-1+ln t+1=ln t,
所以h(t)在(0,1)上单调递减,在(1,+∞)上单调递增,所以h(t)>h(1)=0,
即g(x)<1成立.
2.[2022·河北张家口三模]已知函数g(x)=a ln x-(2a-2)x+x2(a∈R)在x=1处取得极值.
(1)求a的值及函数g(x)的极值;
(2)设f(x)=g(x)-t有三个不同的零点x1,x2,x3(x1
由已知g′(1)=0,解得a=3,
∴g′(x)=,
∴当0
在x=3处取得极小值g(3)=3ln 3-.
(2)证明:由(1)知g(x)=3ln x-4x+x2,极大值为g(1)=-,极小值为g(3)=3ln 3-,
由f(x)=g(x)-t有三个不同的零点x1,x2,x3,可知0
∴H′(x)=g′(x)+g′(2-x)=>0,
∴H(x)在(0,1)上单调递增,H(x)
设h(x)=g(x)-g(6-x),x∈(1,3),
h′(x)=g′(x)+g′(6-x)=>0,∴h(x)在(1,3)上单调递增,
∴h(x)
∴结合①②得x1+6>2+x3,
所以x3<4+x1.
同课章节目录
