(统考版)2023高考数学二轮 第三篇 (研重点 保大分)专题五 解析几何 第1讲 直线与圆 课件(33张)
文档属性
| 名称 | (统考版)2023高考数学二轮 第三篇 (研重点 保大分)专题五 解析几何 第1讲 直线与圆 课件(33张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-20 06:00:47 | ||
图片预览











文档简介
(共33张PPT)
第1讲 直线与圆
考点一
考点二
考点三
考点一 直线的方程
——活选方程,注意斜率
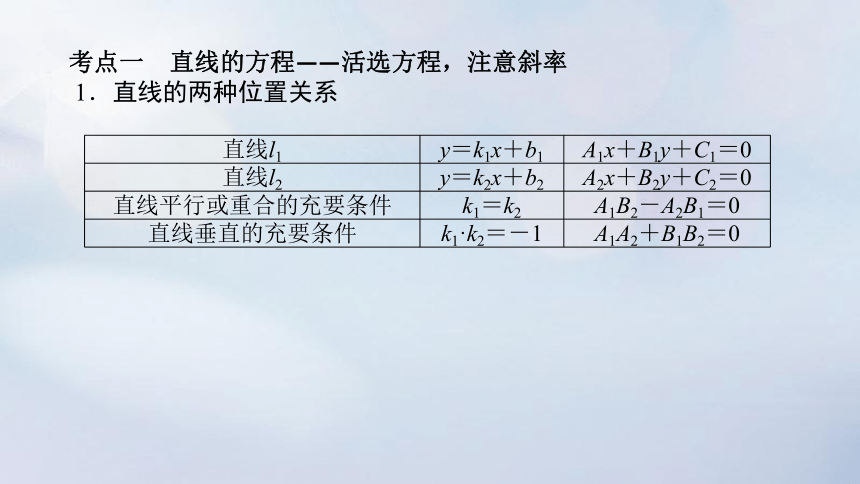
考点一 直线的方程——活选方程,注意斜率
1.直线的两种位置关系
直线l1 y=k1x+b1 A1x+B1y+C1=0
直线l2 y=k2x+b2 A2x+B2y+C2=0
直线平行或重合的充要条件 k1=k2 A1B2-A2B1=0
直线垂直的充要条件 k1·k2=-1 A1A2+B1B2=0
2.三种距离公式
(1)两点间的距离:若A(x1,y1),B(x2,y2),则|AB|= .
(2)点到直线的距离:点P(x0,y0)到直线Ax+By+C=0的距离d=.
(3)两平行线的距离:若直线l1,l2的方程分别为l1:Ax+By+C1=0,l2:Ax+By+C2=0,则两平行线的距离d=.
例 1 (1)[2022·安徽江淮十校第一次联考]“a=-1”是“直线2x+ay+4=0与直线(a-1)x+y+2=0平行”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:C
解析:由两直线平行,得1×2-(a-1)a=0,解得a=2或a=-1,检验:当a=2时,两直线重合,舍去;当a=-1时,两直线平行,所以“a=-1”是“直线2x+ay+4=0与直线(a-1)x+y+2=0平行”的充要条件,故选C.
(2)[数学文化]我国魏晋时期的数学家刘徽创立了割圆术,也就是用内接正多边形去逐步逼近圆,即圆内接正多边形边数无限增加时,其周长就越逼近圆周长,这种用极限思想解决数学问题的方法是数学史上的一项重大成就.现作出圆x2+y2=2的一个内接正八边形,使该正八边形的其中4个顶点在坐标轴上,则下列4条直线中不是该正八边形的一条边所在直线的为( )
A.x+(-1)y-=0
B.(1-)x-y+=0
C.x-(+1)y+=0
D.(-1)x-y+=0
答案:C
解析:如图所示,可知A(,0),B(1,1),C(0,),D(-1,1),所以直线AB,BC,CD的方程分别为y=·(x-),y=(1-)x+,
y=(-1)x+.
整理为一般式即
x+(-1)y-=0,
(1-)x-y+=0,
(-1)x-y+=0.故选C.
归纳总结
求解直线方程的两种方法
直接法 根据已知条件,选择适当的直线方程形式,直接写出直线方程.
待定 系数法 ①设出所求直线方程的恰当形式(点斜式、斜截式、两点式、截距式或一般式);
②由条件建立所求参数的方程(组);
③解这个方程(组)求出参数;
④把参数的值代入所设直线方程.
提醒 (1)忽略直线斜率不存在的情况
在解决有关直线问题时要考虑直线斜率是否存在.
(2)忽略检验致误
求解两条直线平行的问题时,在利用A1B2-A2B1=0建立方程求出参数的值后,要注意代入检验,排除两条直线重合的可能性.
对点训练
1.[2022·湖北黄石高二期末]“m=2”是“直线2x+(m+1)y+4=0与直线3x-my-2=0垂直”的( )
A.充要条件
B.充分不必要条件
C.必要不充分条件
D.既不充分也不必要条件
答案:B
解析:直线2x+(m+1)y+4=0与直线3x-my-2=0垂直,则2×3+(m+1)×(-m)=0,解得m=2或m=-3,
所以“m=2”是“直线2x+(m+1)y+4=0与直线3x-my-2=0垂直”的充分不必要条件.故选B.
2.[2022·北京西城高三模拟]已知直线(2t-3)x+y+5=0不通过第一
象限,则实数t的取值范围为________.
解析:由题意得直线(2t-3)x+y+5=0恒过定点(0,-5),且斜率为-(2t-3),
∵直线(2t-3)x+y+5=0不通过第一象限,
∴-(2t-3)≤0,解得t≥,
故实数t的取值范围是.
考点二 圆的方程
——“几何”、“代数”巧选取
考点二 圆的方程——“几何”、“代数”巧选取
1.圆的标准方程
当圆心为(a,b),半径为r时,其标准方程为(x-a)2+(y-b)2=r2,特别地,当圆心在原点时,方程为x2+y2=r2.
2.圆的一般方程
x2+y2+Dx+Ey+F=0,其中D2+E2-4F>0,表示以为圆心,为半径的圆.
例 2 (1)[2022·全国乙卷]过四点(0,0),(4,0),(-1,1),(4,2)中的三点的一个圆的方程为__________________.
(x-2)2+(y-3)2=13
解析:设点A(0,0),B(4,0),C(-1,1),D(4,2).①若圆过A,B,C三点,则圆心在直线x=2上,设圆心坐标为(2,a),则4+a2=9+(a-1)2,解得a=3,则半径r==,所以圆的方程为(x-2)2+(y-3)2=13.②若圆过A,B,D三点,设圆心坐标为(2,a),则4+a2=4+(a-2)2,解得a=1,则半径r==,所以圆的方程为(x-2)2+(y-1)2=5.③若圆过A,C,D三点,易求线段AC的中垂线方程为y=x+1,线段AD的中垂线方程为y=-2x+5.联立得方程组解得则半径r==,所以圆的方程为+=.④若圆过B,C,D三点,易求线段BD的中垂线方程为y=1,线段BC的中垂线方程为y=5x-7.联立得方程组解得则半径r==,所以圆的方程为+(y-1)2=.
(2)[2022·全国甲卷]设点M在直线2x+y-1=0上,点(3,0)和(0,1)均在⊙M上,则⊙M的方程为________________.
(x-1)2+(y+1)2=5
解析:因为点M在直线2x+y-1=0上,所以设M(a,1-2a).由点(3,0),(0,1)均在⊙M上,可得点(3,0),(0,1)到圆心M的距离相等且为⊙M的半径,所以r==,解得a=1.所以M(1,-1),r=,所以⊙M的方程为(x-1)2+(y+1)2=5.
归纳总结
圆的方程的求法
(1)几何法:通过研究圆的性质、直线和圆、圆与圆的位置关系,从而求得圆的基本量和方程;
(2)代数法:用待定系数法先设出圆的方程,再由条件求得各系数,从而求得圆的方程.一般采用待定系数法.
对点训练
1.[2022·深圳模拟]已知圆M与直线3x-4y=0及3x-4y+10=0都相切,圆心在直线y=-x-4上,则圆M的方程为( )
A.(x+3)2+(y-1)2=1
B.(x-3)2+(y+1)2=1
C.(x+3)2+(y+1)2=1
D.(x-3)2+(y-1)2=1
答案:C
解析:到两直线3x-4y=0,3x-4y+10=0的距离都相等的直线方程为3x-4y+5=0,
联立解得
又两平行线间的距离为2,所以圆M的半径为1,从而圆M的方程为(x+3)2+(y+1)2=1.
2.[2022·河南安阳模拟预测]已知圆C:(x-2)2+(y-6)2=4,点M为直线l:x-y+8=0上一个动点,过点M作圆C的两条切线,切点分别为A,B,则当四边形CAMB周长取最小值时,四边形CAMB的外接圆方程为( )
A.(x-7)2+(y-1)2=4
B.(x-1)2+(y-7)2=4
C.(x-7)2+(y-1)2=2
D.(x-1)2+(y-7)2=2
答案:D
解析:圆C:(x-2)2+(y-6)2=4的圆心C(2,6),半径r=2,点C到直线l的距离d==2,
依题意,CA⊥AM,四边形CAMB周长为2|CA|+2|AM|=4+2≥4+2=4+2=8,
当且仅当CM⊥l时取“=”,此时直线CM:x+y-8=0,由得点M(0,8),
四边形CAMB的外接圆圆心为线段CM的中点(1,7),半径为,方程为(x-1)2+(y-7)2=2.故选D.
考点三 直线(圆)与圆的位置关系
——紧扣“距离”与“半径”
考点三 直线(圆)与圆的位置关系——紧扣“距离”与“半径”
1.直线与圆的位置关系的判定
(1)代数法:将圆的方程和直线的方程联立起来组成方程组,利用判别式Δ来讨论位置关系:Δ>0 相交;Δ=0 相切;Δ<0 相离;
(2)几何法:把圆心到直线的距离d和半径r的大小加以比较:d<r 相交;d=r 相切;d>r 相离.
2.圆与圆的位置关系的判定
(1)d>r1+r2 两圆外离;
(2)d=r1+r2 两圆外切;
(3)|r1-r2|<d<r1+r2 两圆相交;
(4)d=|r1-r2|(r1≠r2) 两圆内切;
(5)0≤d<|r1-r2|(r1≠r2) 两圆内含.
例 3 (1)[2022·广西柳州模拟预测]已知直线y=kx(k>0)与圆C:(x-2)2+(y-1)2=4相交于A,B两点,=2,则k=( )
A. B. C. D.
答案:B
解析:圆C:(x-2)2+(y-1)2=4的圆心C(2,1),r=2,所以圆心C(2,1)到直线y=kx(k>0)的距离为d,则d=,而d= ==1,所以d==1,解得k=.故选B.
(2)[2022·全国甲卷]若双曲线y2-=1(m>0)的渐近线与圆x2+y2-4y
+3=0相切,则m=________.
解析:由题意,得双曲线的一条渐近线方程为y=,即x-my=0.圆的方程可化为x2+(y-2)2=1,故圆心坐标为(0,2),半径r=1.由渐近线与圆相切,结合点到直线的距离公式,得=1,解得m=±.又因为m>0,所以m=.
(3)(数学文化)阿波罗尼斯证明过这样一个命题:平面内到两定点距离之比为常数k(k>0,k≠1)的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点A,B间的距离为2,动点P满足=,则|PA|2+|PB|2的最小值为( )
A.36-24 B.48-24
C.36 D.24
答案:A
解析:以经过A,B的直线为x轴,线段AB的垂直平分线为y轴,建立平面直角坐标系(图略),则A(-1,0),B(1,0).
设P(x,y)因为=,所以=,
两边平方并整理,得x2+y2-6x+1=0,即(x-3)2+y2=8.
所以点P的轨迹是以(3,0)为圆心,2为半径的圆,则=(x+1)2+y2+(x-1)2+y2=2(x2+y2)+2.
方法一 因为x2+y2-6x+1=0,所以|PA|2+|PB|2=2(x2+6x-1-x2)+2=12x.
由y2=8-(x-3)2≥0,得3-2≤x≤3+2.
所以36-24≤12x≤36+24,
由此可知|PA|2+|PB|2的最小值为36-24.
方法二 由(x-3)2+y2=8,可设(θ∈[0,2π)),
则|PA|2+|PB|2=2(x2+y2)+2=2[(2cos θ+3)2+(2sin θ)2]+2=24cos θ+36.
因为θ∈[0,2π),所以-1≤cos θ≤1,所以36-24≤24cos θ+36≤36+24,
由此可知|PA|2+|PB|2的最小值为36-24.
归纳总结
1.求解圆的弦长的三种方法
关系法
公式法
距离法 联立直线与圆的方程,解方程组求出两交点坐标,用两点间距离公式求解
2.与圆的切线有关的结论
(1)过圆x2+y2=r2外一点P(x0,y0)作圆的两条切线,切点为A,B,则过A,B两点的直线方程为x0x+y0y=r2.
(2)过圆x2+y2+Dx+Ey+F=0(D2+E2-4F>0)外一点P(x0,y0)引圆的切线,切点为T,则切线长为|PT|=.
(3)过圆C:(x-a)2+(y-b)2=r2(r>0)外一点(x0,y0)作圆C的两条切线,切点分别为A,B,则切点弦AB所在直线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2.
对点训练
1.直线l:3x+4y-1=0被圆C:x2+y2-2x-4y-4=0所截得的弦长为( )
A.2 B.4
C.2 D.2
答案:A
解析:由题意圆心C(1,2),圆C的半径为3,
故C到l:3x+4y-1=0的距离为=2,
故所求弦长为2=2.故选A.
2.[2022·安徽合肥市第八中学]直线l:x+my-m-1=0被圆O:x2+y2=3截得的弦长最短,则实数m=________.
1
解析:直线l的方程可化为x-1+m(y-1)=0,
由,得,
所以直线l过定点A(1,1),
因为12+12<3,即点A在圆x2+y2=3内.
当OA⊥l时,|MN|取最小值,
由kOAkl=-1,得1×=-1,∴m=1.
第1讲 直线与圆
考点一
考点二
考点三
考点一 直线的方程
——活选方程,注意斜率
考点一 直线的方程——活选方程,注意斜率
1.直线的两种位置关系
直线l1 y=k1x+b1 A1x+B1y+C1=0
直线l2 y=k2x+b2 A2x+B2y+C2=0
直线平行或重合的充要条件 k1=k2 A1B2-A2B1=0
直线垂直的充要条件 k1·k2=-1 A1A2+B1B2=0
2.三种距离公式
(1)两点间的距离:若A(x1,y1),B(x2,y2),则|AB|= .
(2)点到直线的距离:点P(x0,y0)到直线Ax+By+C=0的距离d=.
(3)两平行线的距离:若直线l1,l2的方程分别为l1:Ax+By+C1=0,l2:Ax+By+C2=0,则两平行线的距离d=.
例 1 (1)[2022·安徽江淮十校第一次联考]“a=-1”是“直线2x+ay+4=0与直线(a-1)x+y+2=0平行”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
答案:C
解析:由两直线平行,得1×2-(a-1)a=0,解得a=2或a=-1,检验:当a=2时,两直线重合,舍去;当a=-1时,两直线平行,所以“a=-1”是“直线2x+ay+4=0与直线(a-1)x+y+2=0平行”的充要条件,故选C.
(2)[数学文化]我国魏晋时期的数学家刘徽创立了割圆术,也就是用内接正多边形去逐步逼近圆,即圆内接正多边形边数无限增加时,其周长就越逼近圆周长,这种用极限思想解决数学问题的方法是数学史上的一项重大成就.现作出圆x2+y2=2的一个内接正八边形,使该正八边形的其中4个顶点在坐标轴上,则下列4条直线中不是该正八边形的一条边所在直线的为( )
A.x+(-1)y-=0
B.(1-)x-y+=0
C.x-(+1)y+=0
D.(-1)x-y+=0
答案:C
解析:如图所示,可知A(,0),B(1,1),C(0,),D(-1,1),所以直线AB,BC,CD的方程分别为y=·(x-),y=(1-)x+,
y=(-1)x+.
整理为一般式即
x+(-1)y-=0,
(1-)x-y+=0,
(-1)x-y+=0.故选C.
归纳总结
求解直线方程的两种方法
直接法 根据已知条件,选择适当的直线方程形式,直接写出直线方程.
待定 系数法 ①设出所求直线方程的恰当形式(点斜式、斜截式、两点式、截距式或一般式);
②由条件建立所求参数的方程(组);
③解这个方程(组)求出参数;
④把参数的值代入所设直线方程.
提醒 (1)忽略直线斜率不存在的情况
在解决有关直线问题时要考虑直线斜率是否存在.
(2)忽略检验致误
求解两条直线平行的问题时,在利用A1B2-A2B1=0建立方程求出参数的值后,要注意代入检验,排除两条直线重合的可能性.
对点训练
1.[2022·湖北黄石高二期末]“m=2”是“直线2x+(m+1)y+4=0与直线3x-my-2=0垂直”的( )
A.充要条件
B.充分不必要条件
C.必要不充分条件
D.既不充分也不必要条件
答案:B
解析:直线2x+(m+1)y+4=0与直线3x-my-2=0垂直,则2×3+(m+1)×(-m)=0,解得m=2或m=-3,
所以“m=2”是“直线2x+(m+1)y+4=0与直线3x-my-2=0垂直”的充分不必要条件.故选B.
2.[2022·北京西城高三模拟]已知直线(2t-3)x+y+5=0不通过第一
象限,则实数t的取值范围为________.
解析:由题意得直线(2t-3)x+y+5=0恒过定点(0,-5),且斜率为-(2t-3),
∵直线(2t-3)x+y+5=0不通过第一象限,
∴-(2t-3)≤0,解得t≥,
故实数t的取值范围是.
考点二 圆的方程
——“几何”、“代数”巧选取
考点二 圆的方程——“几何”、“代数”巧选取
1.圆的标准方程
当圆心为(a,b),半径为r时,其标准方程为(x-a)2+(y-b)2=r2,特别地,当圆心在原点时,方程为x2+y2=r2.
2.圆的一般方程
x2+y2+Dx+Ey+F=0,其中D2+E2-4F>0,表示以为圆心,为半径的圆.
例 2 (1)[2022·全国乙卷]过四点(0,0),(4,0),(-1,1),(4,2)中的三点的一个圆的方程为__________________.
(x-2)2+(y-3)2=13
解析:设点A(0,0),B(4,0),C(-1,1),D(4,2).①若圆过A,B,C三点,则圆心在直线x=2上,设圆心坐标为(2,a),则4+a2=9+(a-1)2,解得a=3,则半径r==,所以圆的方程为(x-2)2+(y-3)2=13.②若圆过A,B,D三点,设圆心坐标为(2,a),则4+a2=4+(a-2)2,解得a=1,则半径r==,所以圆的方程为(x-2)2+(y-1)2=5.③若圆过A,C,D三点,易求线段AC的中垂线方程为y=x+1,线段AD的中垂线方程为y=-2x+5.联立得方程组解得则半径r==,所以圆的方程为+=.④若圆过B,C,D三点,易求线段BD的中垂线方程为y=1,线段BC的中垂线方程为y=5x-7.联立得方程组解得则半径r==,所以圆的方程为+(y-1)2=.
(2)[2022·全国甲卷]设点M在直线2x+y-1=0上,点(3,0)和(0,1)均在⊙M上,则⊙M的方程为________________.
(x-1)2+(y+1)2=5
解析:因为点M在直线2x+y-1=0上,所以设M(a,1-2a).由点(3,0),(0,1)均在⊙M上,可得点(3,0),(0,1)到圆心M的距离相等且为⊙M的半径,所以r==,解得a=1.所以M(1,-1),r=,所以⊙M的方程为(x-1)2+(y+1)2=5.
归纳总结
圆的方程的求法
(1)几何法:通过研究圆的性质、直线和圆、圆与圆的位置关系,从而求得圆的基本量和方程;
(2)代数法:用待定系数法先设出圆的方程,再由条件求得各系数,从而求得圆的方程.一般采用待定系数法.
对点训练
1.[2022·深圳模拟]已知圆M与直线3x-4y=0及3x-4y+10=0都相切,圆心在直线y=-x-4上,则圆M的方程为( )
A.(x+3)2+(y-1)2=1
B.(x-3)2+(y+1)2=1
C.(x+3)2+(y+1)2=1
D.(x-3)2+(y-1)2=1
答案:C
解析:到两直线3x-4y=0,3x-4y+10=0的距离都相等的直线方程为3x-4y+5=0,
联立解得
又两平行线间的距离为2,所以圆M的半径为1,从而圆M的方程为(x+3)2+(y+1)2=1.
2.[2022·河南安阳模拟预测]已知圆C:(x-2)2+(y-6)2=4,点M为直线l:x-y+8=0上一个动点,过点M作圆C的两条切线,切点分别为A,B,则当四边形CAMB周长取最小值时,四边形CAMB的外接圆方程为( )
A.(x-7)2+(y-1)2=4
B.(x-1)2+(y-7)2=4
C.(x-7)2+(y-1)2=2
D.(x-1)2+(y-7)2=2
答案:D
解析:圆C:(x-2)2+(y-6)2=4的圆心C(2,6),半径r=2,点C到直线l的距离d==2,
依题意,CA⊥AM,四边形CAMB周长为2|CA|+2|AM|=4+2≥4+2=4+2=8,
当且仅当CM⊥l时取“=”,此时直线CM:x+y-8=0,由得点M(0,8),
四边形CAMB的外接圆圆心为线段CM的中点(1,7),半径为,方程为(x-1)2+(y-7)2=2.故选D.
考点三 直线(圆)与圆的位置关系
——紧扣“距离”与“半径”
考点三 直线(圆)与圆的位置关系——紧扣“距离”与“半径”
1.直线与圆的位置关系的判定
(1)代数法:将圆的方程和直线的方程联立起来组成方程组,利用判别式Δ来讨论位置关系:Δ>0 相交;Δ=0 相切;Δ<0 相离;
(2)几何法:把圆心到直线的距离d和半径r的大小加以比较:d<r 相交;d=r 相切;d>r 相离.
2.圆与圆的位置关系的判定
(1)d>r1+r2 两圆外离;
(2)d=r1+r2 两圆外切;
(3)|r1-r2|<d<r1+r2 两圆相交;
(4)d=|r1-r2|(r1≠r2) 两圆内切;
(5)0≤d<|r1-r2|(r1≠r2) 两圆内含.
例 3 (1)[2022·广西柳州模拟预测]已知直线y=kx(k>0)与圆C:(x-2)2+(y-1)2=4相交于A,B两点,=2,则k=( )
A. B. C. D.
答案:B
解析:圆C:(x-2)2+(y-1)2=4的圆心C(2,1),r=2,所以圆心C(2,1)到直线y=kx(k>0)的距离为d,则d=,而d= ==1,所以d==1,解得k=.故选B.
(2)[2022·全国甲卷]若双曲线y2-=1(m>0)的渐近线与圆x2+y2-4y
+3=0相切,则m=________.
解析:由题意,得双曲线的一条渐近线方程为y=,即x-my=0.圆的方程可化为x2+(y-2)2=1,故圆心坐标为(0,2),半径r=1.由渐近线与圆相切,结合点到直线的距离公式,得=1,解得m=±.又因为m>0,所以m=.
(3)(数学文化)阿波罗尼斯证明过这样一个命题:平面内到两定点距离之比为常数k(k>0,k≠1)的点的轨迹是圆,后人将这个圆称为阿波罗尼斯圆.若平面内两定点A,B间的距离为2,动点P满足=,则|PA|2+|PB|2的最小值为( )
A.36-24 B.48-24
C.36 D.24
答案:A
解析:以经过A,B的直线为x轴,线段AB的垂直平分线为y轴,建立平面直角坐标系(图略),则A(-1,0),B(1,0).
设P(x,y)因为=,所以=,
两边平方并整理,得x2+y2-6x+1=0,即(x-3)2+y2=8.
所以点P的轨迹是以(3,0)为圆心,2为半径的圆,则=(x+1)2+y2+(x-1)2+y2=2(x2+y2)+2.
方法一 因为x2+y2-6x+1=0,所以|PA|2+|PB|2=2(x2+6x-1-x2)+2=12x.
由y2=8-(x-3)2≥0,得3-2≤x≤3+2.
所以36-24≤12x≤36+24,
由此可知|PA|2+|PB|2的最小值为36-24.
方法二 由(x-3)2+y2=8,可设(θ∈[0,2π)),
则|PA|2+|PB|2=2(x2+y2)+2=2[(2cos θ+3)2+(2sin θ)2]+2=24cos θ+36.
因为θ∈[0,2π),所以-1≤cos θ≤1,所以36-24≤24cos θ+36≤36+24,
由此可知|PA|2+|PB|2的最小值为36-24.
归纳总结
1.求解圆的弦长的三种方法
关系法
公式法
距离法 联立直线与圆的方程,解方程组求出两交点坐标,用两点间距离公式求解
2.与圆的切线有关的结论
(1)过圆x2+y2=r2外一点P(x0,y0)作圆的两条切线,切点为A,B,则过A,B两点的直线方程为x0x+y0y=r2.
(2)过圆x2+y2+Dx+Ey+F=0(D2+E2-4F>0)外一点P(x0,y0)引圆的切线,切点为T,则切线长为|PT|=.
(3)过圆C:(x-a)2+(y-b)2=r2(r>0)外一点(x0,y0)作圆C的两条切线,切点分别为A,B,则切点弦AB所在直线方程为(x0-a)(x-a)+(y0-b)(y-b)=r2.
对点训练
1.直线l:3x+4y-1=0被圆C:x2+y2-2x-4y-4=0所截得的弦长为( )
A.2 B.4
C.2 D.2
答案:A
解析:由题意圆心C(1,2),圆C的半径为3,
故C到l:3x+4y-1=0的距离为=2,
故所求弦长为2=2.故选A.
2.[2022·安徽合肥市第八中学]直线l:x+my-m-1=0被圆O:x2+y2=3截得的弦长最短,则实数m=________.
1
解析:直线l的方程可化为x-1+m(y-1)=0,
由,得,
所以直线l过定点A(1,1),
因为12+12<3,即点A在圆x2+y2=3内.
当OA⊥l时,|MN|取最小值,
由kOAkl=-1,得1×=-1,∴m=1.
同课章节目录
