浙江省宁波市2013-2014学年高一下学期期末考试数学试题
文档属性
| 名称 | 浙江省宁波市2013-2014学年高一下学期期末考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 243.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-07-03 15:12:29 | ||
图片预览



文档简介
一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设、、,,则下列不等式一定成立的是
2.数列:、3、、9、…的一个通项公式是
() ()
() ()
3.设是两条不同的直线,是一个平面,则下列命题不正确的是
若,,则 若,∥,则
若,,则∥ 若∥,∥,则∥
4.等差数列的前项和为,若,,则
12 16
5.在中,角所对的边分别为,那么下列给出的各组条件能确定三角形有两解的是
,, ,,
,, ,,
6. 已知数列满足,,则
2
7.当时,关于的不等式的解集是
8.已知函数的图象的一个对称中心是点,则函数=的图象的一条对称轴是直线
9.若不等式对任意的上恒成立,则的取值范围是
10.如图,三棱柱的各棱长均为2,侧棱与底面所成的角为,为锐角,且侧面⊥底面,给出下列四个结论:
①;
②;
③直线与平面所成的角为;
④.
其中正确的结论是
①③ ②④ ①③④ ①②③④
二、填空题:本大题共7个小题,每小题4分,共28分.
把答案填在答题卷的相应位置
11.求值: ___________.
12.圆锥的母线长为3,侧面展开图的中心角为,那么它的表面积为___________.
13.将棱长为2的正方体切割后得一几何体,其三视图如图所示,
则该几何体的体积为___________.
14.正数、满足,那么的最小值等于
___________.
15.已知数列是首项为3,公差为1的等差数列,数列
是首项为,公比也为的等比数列,其中,那么数
列的前项和________.
16.在中,角所对的边分别为,若成等差数列,则角
的取值范围是__________(角用弧度表示).
17.在数列中,,, (),把数列的各项按如下方法进行分组:()、()、()、……,记为第组的第个数(从前到后),若=,则____________.
三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.
18.(本题满分14分)
(Ⅰ)已知,,求的值;
(Ⅱ)已知,,,求的值.
19.(本题满分14分)
在中,分别是角所对的边,且.
(Ⅰ)求角;
(Ⅱ)若,求的周长的取值范围.
20.(本题满分14分)
某市环保部门对市中心每天环境污染情况进行调查研究,发现一天中环境污染指数与时刻(时)的关系为,,其中是与气象有关的参数,且,用每天的最大值作为当天的污染指数,记作.
(Ⅰ)令,,求的取值范围;
(Ⅱ)按规定,每天的污染指数不得超过2,问目前市中心的污染指数是否超标?
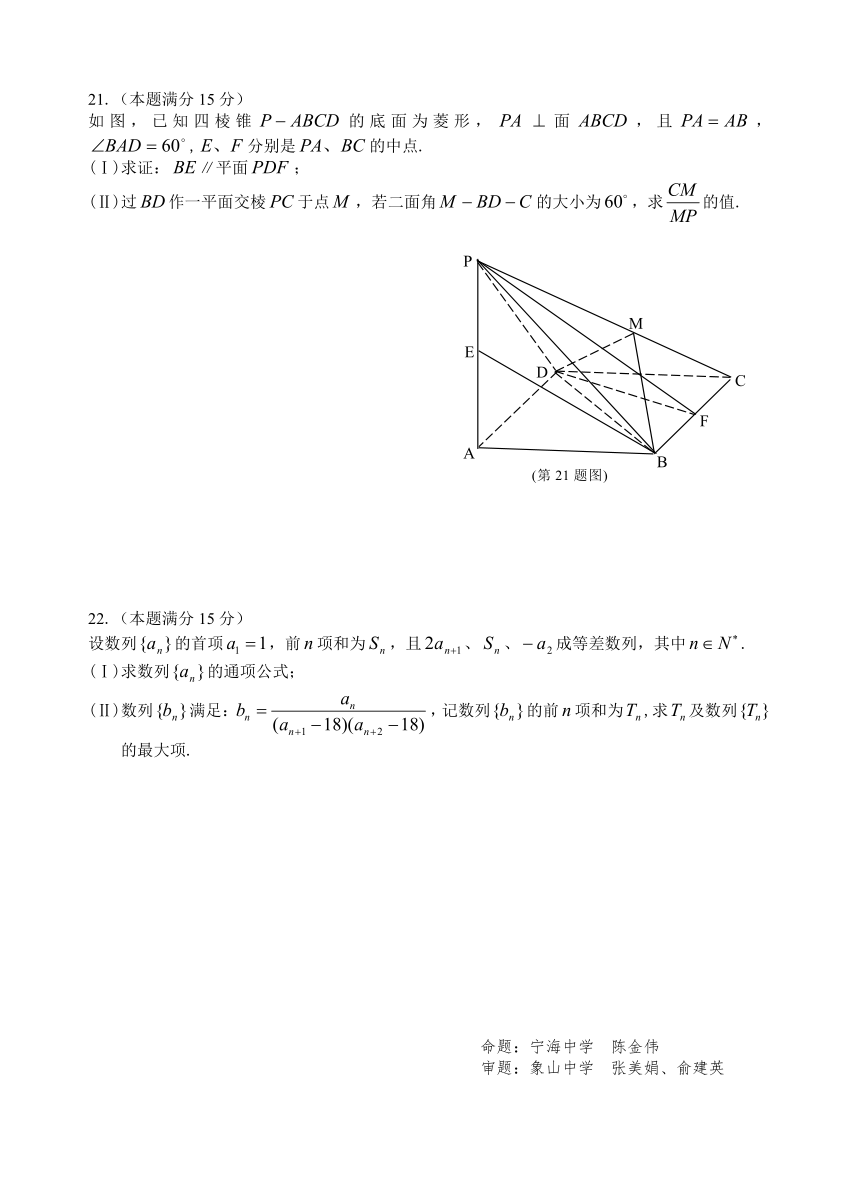
21.(本题满分15分)
如图,已知四棱锥的底面为菱形,面,且,,分别是的中点.
(Ⅰ)求证:∥平面;
(Ⅱ)过作一平面交棱于点,若二面角的大小为,求的值.
22.(本题满分15分)
设数列的首项,前项和为,且、、成等差数列,其中.
(Ⅰ)求数列的通项公式;
(Ⅱ)数列满足:,记数列的前项和为,求及数列的最大项.
命题:宁海中学 陈金伟
审题:象山中学 张美娟、俞建英
宁波市 八校联考高一数学参考答案
三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.
18.(本题满分14分)
因为,,所以,, ……5分
. ………………………………………………7分
(Ⅱ)因为且,所以, ……………………………9分
因为,所以,
又,所以,所以,……11分
所以.……………………………14分
因为,所以,,
,所以,即. ………14分
法2:由余弦定理得,, …………9分
而,故,………………11分
所以, …………………………………………………………………12分
又, ……………………………………………………………………13分
所以,即. ………………………………14分
20.(本题满分14分)
(Ⅰ)(1)当时,;………………………………………………………………1分
在上单调递减,在上单调递增,所以的最大值只可能在或
21.(本题满分15分)
(Ⅰ)取的中点,连结、,
因为是的中点,所以∥,且
,又是菱形边
的中点,所以∥,且,
所以∥,且,四边形
是平行四边形,所以∥,
……………………………………………5分
而平面,平面,……………………………………………6分
所以∥平面.…………………………………………………………………7分
(Ⅱ)连结交于,连结,因为面,所以,即
,又,且,所以平面,…………10分
从而,,所以就是二面角的平面角,,………………………………………………………………………12分
设,因为,,所以,,,
,所以,在中,,…14分
所以 ……………………………………………………………15分
22.(本题满分15分)
(Ⅰ) 由、、成等差数列知,,………………………1分
当时,,
所以, ……………………………………4分
当时,由得, ……………………………………5分
综上知,对任何,都有,又,所以,.…6分
所以数列是首项为1,公比为2的等比数列,所以. ……………7分
(Ⅱ) ……10分
,……………………………12分
,
当时,,即;当时,也有,但;当时,,,即.
所以数列的的最大项是. ……………………………………………15分
A
A1
C
B
C1
B1
(第10题图)
正视图
侧视图
俯视图
视图
(第13题图)
P
M
F
A
D
E
C
B
(第21题图)图
2013学年
第二学期
P
M
F
A
D
E
C
B
(第21题图)图
G
O
1.设、、,,则下列不等式一定成立的是
2.数列:、3、、9、…的一个通项公式是
() ()
() ()
3.设是两条不同的直线,是一个平面,则下列命题不正确的是
若,,则 若,∥,则
若,,则∥ 若∥,∥,则∥
4.等差数列的前项和为,若,,则
12 16
5.在中,角所对的边分别为,那么下列给出的各组条件能确定三角形有两解的是
,, ,,
,, ,,
6. 已知数列满足,,则
2
7.当时,关于的不等式的解集是
8.已知函数的图象的一个对称中心是点,则函数=的图象的一条对称轴是直线
9.若不等式对任意的上恒成立,则的取值范围是
10.如图,三棱柱的各棱长均为2,侧棱与底面所成的角为,为锐角,且侧面⊥底面,给出下列四个结论:
①;
②;
③直线与平面所成的角为;
④.
其中正确的结论是
①③ ②④ ①③④ ①②③④
二、填空题:本大题共7个小题,每小题4分,共28分.
把答案填在答题卷的相应位置
11.求值: ___________.
12.圆锥的母线长为3,侧面展开图的中心角为,那么它的表面积为___________.
13.将棱长为2的正方体切割后得一几何体,其三视图如图所示,
则该几何体的体积为___________.
14.正数、满足,那么的最小值等于
___________.
15.已知数列是首项为3,公差为1的等差数列,数列
是首项为,公比也为的等比数列,其中,那么数
列的前项和________.
16.在中,角所对的边分别为,若成等差数列,则角
的取值范围是__________(角用弧度表示).
17.在数列中,,, (),把数列的各项按如下方法进行分组:()、()、()、……,记为第组的第个数(从前到后),若=,则____________.
三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.
18.(本题满分14分)
(Ⅰ)已知,,求的值;
(Ⅱ)已知,,,求的值.
19.(本题满分14分)
在中,分别是角所对的边,且.
(Ⅰ)求角;
(Ⅱ)若,求的周长的取值范围.
20.(本题满分14分)
某市环保部门对市中心每天环境污染情况进行调查研究,发现一天中环境污染指数与时刻(时)的关系为,,其中是与气象有关的参数,且,用每天的最大值作为当天的污染指数,记作.
(Ⅰ)令,,求的取值范围;
(Ⅱ)按规定,每天的污染指数不得超过2,问目前市中心的污染指数是否超标?
21.(本题满分15分)
如图,已知四棱锥的底面为菱形,面,且,,分别是的中点.
(Ⅰ)求证:∥平面;
(Ⅱ)过作一平面交棱于点,若二面角的大小为,求的值.
22.(本题满分15分)
设数列的首项,前项和为,且、、成等差数列,其中.
(Ⅰ)求数列的通项公式;
(Ⅱ)数列满足:,记数列的前项和为,求及数列的最大项.
命题:宁海中学 陈金伟
审题:象山中学 张美娟、俞建英
宁波市 八校联考高一数学参考答案
三、解答题:本大题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.
18.(本题满分14分)
因为,,所以,, ……5分
. ………………………………………………7分
(Ⅱ)因为且,所以, ……………………………9分
因为,所以,
又,所以,所以,……11分
所以.……………………………14分
因为,所以,,
,所以,即. ………14分
法2:由余弦定理得,, …………9分
而,故,………………11分
所以, …………………………………………………………………12分
又, ……………………………………………………………………13分
所以,即. ………………………………14分
20.(本题满分14分)
(Ⅰ)(1)当时,;………………………………………………………………1分
在上单调递减,在上单调递增,所以的最大值只可能在或
21.(本题满分15分)
(Ⅰ)取的中点,连结、,
因为是的中点,所以∥,且
,又是菱形边
的中点,所以∥,且,
所以∥,且,四边形
是平行四边形,所以∥,
……………………………………………5分
而平面,平面,……………………………………………6分
所以∥平面.…………………………………………………………………7分
(Ⅱ)连结交于,连结,因为面,所以,即
,又,且,所以平面,…………10分
从而,,所以就是二面角的平面角,,………………………………………………………………………12分
设,因为,,所以,,,
,所以,在中,,…14分
所以 ……………………………………………………………15分
22.(本题满分15分)
(Ⅰ) 由、、成等差数列知,,………………………1分
当时,,
所以, ……………………………………4分
当时,由得, ……………………………………5分
综上知,对任何,都有,又,所以,.…6分
所以数列是首项为1,公比为2的等比数列,所以. ……………7分
(Ⅱ) ……10分
,……………………………12分
,
当时,,即;当时,也有,但;当时,,,即.
所以数列的的最大项是. ……………………………………………15分
A
A1
C
B
C1
B1
(第10题图)
正视图
侧视图
俯视图
视图
(第13题图)
P
M
F
A
D
E
C
B
(第21题图)图
2013学年
第二学期
P
M
F
A
D
E
C
B
(第21题图)图
G
O
同课章节目录
