福建省福州市八县一中2013-2014学年高一下学期期末联考数学试题
文档属性
| 名称 | 福建省福州市八县一中2013-2014学年高一下学期期末联考数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 285.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-07-04 08:23:40 | ||
图片预览



文档简介
一、选择题(共12小题,每题5分,共60分)
1.计算sin(-)的值为 ( ).
A.- B. C. D.-
2.半径为3,中心角为120o的扇形面积为( )
A. B. C. D.
3.如图,在直角坐标系xOy中,射线OP交单位圆O于点P,若∠XOP =θ,则点P的坐标是( )
A.(cosθ,sinθ) B. (-cosθ,sinθ)
C.(sinθ,cosθ) D.(-sinθ,cosθ)
4.sin55°sin65°- cos55°cos65°值为( )
A. B. C.- D.-
5.已知向量=(-1,x), = (1,x),若2-与垂直,则( )
A. B. C. D.4
6.A、B、D三点共线,则对任一点C,=,则λ=( )
A. B. C.- D. -
7.已知cos()=,则sin 2的值为 ( )
A. B.- C. D.-
8.函数f(x)=2sinxcosx+cos2x的最小正周期和振幅分别是( )
A.π,1 B.π,2 C.2π,1 D.2π,2
9.如图,已知中,AB=3,AC=4,BC=5,AD⊥BC于D点,点为
边所在直线上的一个动点,则满足( )
A.最大值为9 B.为定值
C.最小值为3 D.与的位置有关
10.把函数的图像向左平移个单位可以得到函数 的图像,若的图像关于y轴对称,则的值为( )
A. B. C.或 D.
11.在ABC中,=,=, 且满足:||=1, ||=2, ||=,则·+·+·的值为( )
A.4 B. C.-4 D.-
12.若两个函数的图像仅经过若干次平移能够重合,则称这两个函数为“同形”函数,给出下列三个函数:f1(x)=2cos2x, f2(x)=sinx+cosx, f3(x)=2cos(x-)-1, 则( )
A.f1(x),f2(x),f3(x)两两为“同形”函数;
B.f1(x),f2(x),f3(x)两两不为“同形”函数;
C.f1(x), f2(x) 为“同形”函数,且它们与f3(x) 不为“同形”函数;
D.f2(x),f3(x) 为“同形”函数,且它们与f1(x) 不为“同形”函数;
二、填空题(共4小题,每题4分,共16分)
13.++=
14.化简:=
15.如图,在半径为2,中心角为的扇形的内接矩形OABC
(只有B在弧上)的面积的最大值=
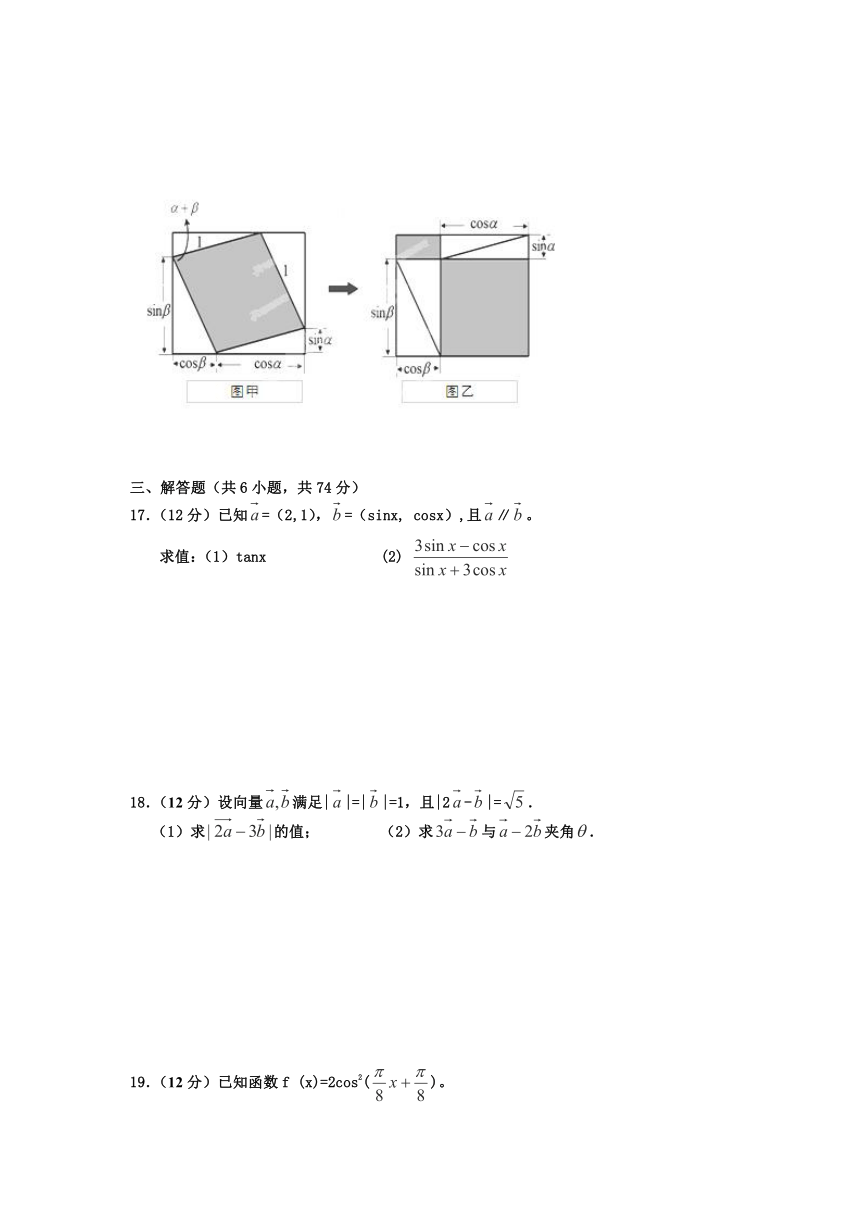
16.“无字证明”(proofs without words), 就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.请利用图甲、图乙中阴影部分的面积关系,写出该图所验证的一个三角恒等变换公式: .
三、解答题(共6小题,共74分)
17.(12分)已知=(2,1),=(sinx, cosx),且∥。
求值:(1)tanx (2)
18.(12分)设向量满足||=||=1,且|2-|=.
(1)求的值; (2)求与夹角.
19.(12分)已知函数f (x)=2cos2()。
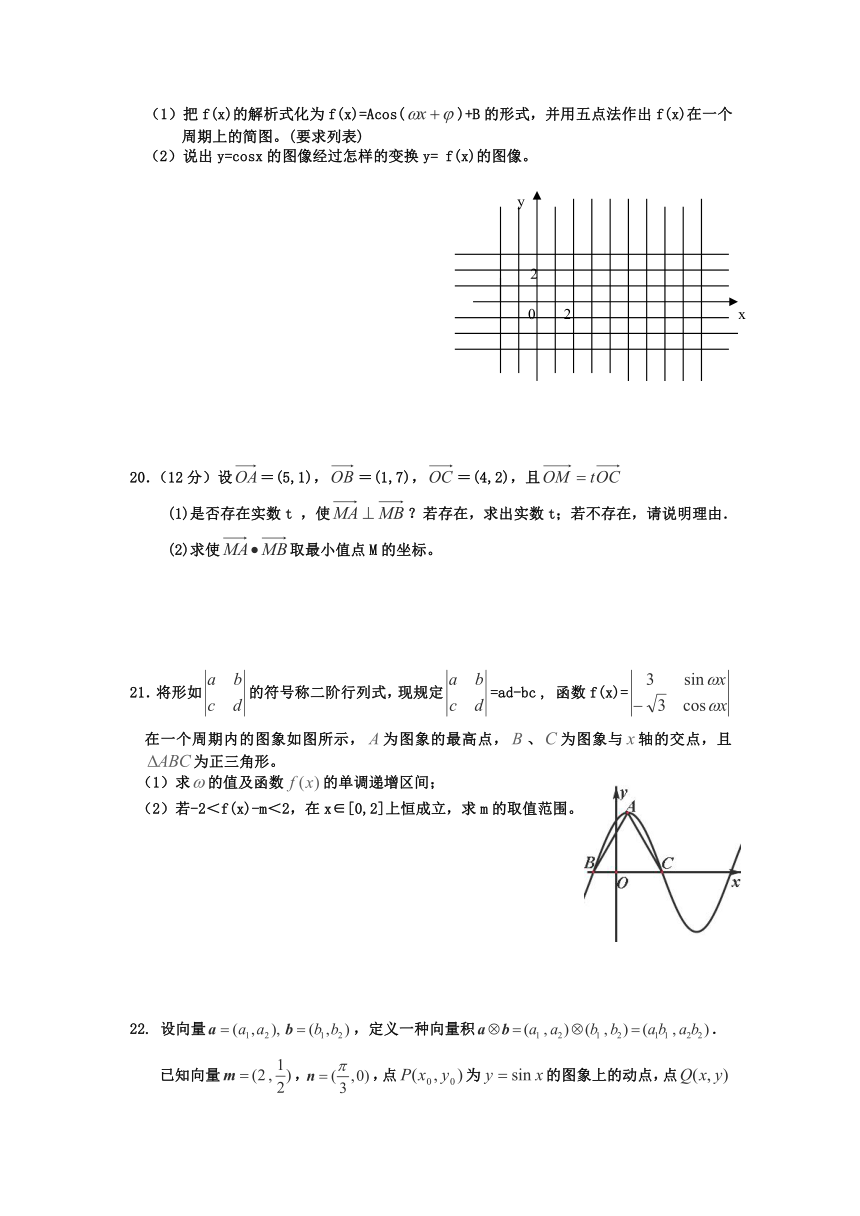
(1)把f(x)的解析式化为f(x)=Acos()+B的形式,并用五点法作出f(x)在一个周期上的简图。(要求列表)
(2)说出y=cosx的图像经过怎样的变换y= f(x)的图像。
20.(12分)设=(5,1),=(1,7),=(4,2),且
(1)是否存在实数t ,使?若存在,求出实数t;若不存在,请说明理由.
(2)求使取最小值点M的坐标。
21.将形如的符号称二阶行列式,现规定=ad-bc , 函数f(x)=在一个周期内的图象如图所示,为图象的最高点,、为图象与轴的交点,且为正三角形。
(1)求的值及函数的单调递增区间;
(2)若-2<f(x)-m<2,在x∈[0,2]上恒成立,求m的取值范围。
22. 设向量,定义一种向量积.
已知向量,,点为的图象上的动点,点 为的图象上的动点,且满足(其中为坐标原点).
(Ⅰ)请用表示;
(Ⅱ)求的表达式并求它的周期;
(Ⅲ)把函数图象上各点的横坐标缩小为原来的倍(纵坐标不变),得到函数的图象.设函数,试讨论函数在区间内的零点个数.
2013---2014学年度第二学期八县(市)一中期末联考
高中 一 年 数学 科答题卷
考试日期: 7月1 日 完卷时间: 120 分钟 满分: 150 分
1~12 13~16 17 18 19 20 21 22 总分
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
一、选择题:(每小题 5 分,共 60 分)
二、填空题:(每题 4 分,共 16 分)
13 14
15 16
三、解答题:
17.(12分)
………6分
作图3分
21,(1) f(x)==3cosωx+ sinωx
=2(cosωx+sinωx)=2sin(ωx+)…3分
f(x)max=2∴BC=4,=4,T=8=,∴ω= ……5分
∴f(x)=2sin(x+)
单调递增区间:……7分
(2)依题意,在x∈[0,2]时恒成立,
∴……10分
学校 班级 姓名 座号 准考号: .
命题学校: 长乐一中 命题教师: 葛凤清 复核教师: 吴丽娜
---------密………封…………装…………订………线----------
. .
2
0
y
x
x
22.(14分)
20.(12分)
21.(12分)
2
18.(12分)
19.(12分)
(1)
(2)y=cosx y =
y =
y=
C
1.计算sin(-)的值为 ( ).
A.- B. C. D.-
2.半径为3,中心角为120o的扇形面积为( )
A. B. C. D.
3.如图,在直角坐标系xOy中,射线OP交单位圆O于点P,若∠XOP =θ,则点P的坐标是( )
A.(cosθ,sinθ) B. (-cosθ,sinθ)
C.(sinθ,cosθ) D.(-sinθ,cosθ)
4.sin55°sin65°- cos55°cos65°值为( )
A. B. C.- D.-
5.已知向量=(-1,x), = (1,x),若2-与垂直,则( )
A. B. C. D.4
6.A、B、D三点共线,则对任一点C,=,则λ=( )
A. B. C.- D. -
7.已知cos()=,则sin 2的值为 ( )
A. B.- C. D.-
8.函数f(x)=2sinxcosx+cos2x的最小正周期和振幅分别是( )
A.π,1 B.π,2 C.2π,1 D.2π,2
9.如图,已知中,AB=3,AC=4,BC=5,AD⊥BC于D点,点为
边所在直线上的一个动点,则满足( )
A.最大值为9 B.为定值
C.最小值为3 D.与的位置有关
10.把函数的图像向左平移个单位可以得到函数 的图像,若的图像关于y轴对称,则的值为( )
A. B. C.或 D.
11.在ABC中,=,=, 且满足:||=1, ||=2, ||=,则·+·+·的值为( )
A.4 B. C.-4 D.-
12.若两个函数的图像仅经过若干次平移能够重合,则称这两个函数为“同形”函数,给出下列三个函数:f1(x)=2cos2x, f2(x)=sinx+cosx, f3(x)=2cos(x-)-1, 则( )
A.f1(x),f2(x),f3(x)两两为“同形”函数;
B.f1(x),f2(x),f3(x)两两不为“同形”函数;
C.f1(x), f2(x) 为“同形”函数,且它们与f3(x) 不为“同形”函数;
D.f2(x),f3(x) 为“同形”函数,且它们与f1(x) 不为“同形”函数;
二、填空题(共4小题,每题4分,共16分)
13.++=
14.化简:=
15.如图,在半径为2,中心角为的扇形的内接矩形OABC
(只有B在弧上)的面积的最大值=
16.“无字证明”(proofs without words), 就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.请利用图甲、图乙中阴影部分的面积关系,写出该图所验证的一个三角恒等变换公式: .
三、解答题(共6小题,共74分)
17.(12分)已知=(2,1),=(sinx, cosx),且∥。
求值:(1)tanx (2)
18.(12分)设向量满足||=||=1,且|2-|=.
(1)求的值; (2)求与夹角.
19.(12分)已知函数f (x)=2cos2()。
(1)把f(x)的解析式化为f(x)=Acos()+B的形式,并用五点法作出f(x)在一个周期上的简图。(要求列表)
(2)说出y=cosx的图像经过怎样的变换y= f(x)的图像。
20.(12分)设=(5,1),=(1,7),=(4,2),且
(1)是否存在实数t ,使?若存在,求出实数t;若不存在,请说明理由.
(2)求使取最小值点M的坐标。
21.将形如的符号称二阶行列式,现规定=ad-bc , 函数f(x)=在一个周期内的图象如图所示,为图象的最高点,、为图象与轴的交点,且为正三角形。
(1)求的值及函数的单调递增区间;
(2)若-2<f(x)-m<2,在x∈[0,2]上恒成立,求m的取值范围。
22. 设向量,定义一种向量积.
已知向量,,点为的图象上的动点,点 为的图象上的动点,且满足(其中为坐标原点).
(Ⅰ)请用表示;
(Ⅱ)求的表达式并求它的周期;
(Ⅲ)把函数图象上各点的横坐标缩小为原来的倍(纵坐标不变),得到函数的图象.设函数,试讨论函数在区间内的零点个数.
2013---2014学年度第二学期八县(市)一中期末联考
高中 一 年 数学 科答题卷
考试日期: 7月1 日 完卷时间: 120 分钟 满分: 150 分
1~12 13~16 17 18 19 20 21 22 总分
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
一、选择题:(每小题 5 分,共 60 分)
二、填空题:(每题 4 分,共 16 分)
13 14
15 16
三、解答题:
17.(12分)
………6分
作图3分
21,(1) f(x)==3cosωx+ sinωx
=2(cosωx+sinωx)=2sin(ωx+)…3分
f(x)max=2∴BC=4,=4,T=8=,∴ω= ……5分
∴f(x)=2sin(x+)
单调递增区间:……7分
(2)依题意,在x∈[0,2]时恒成立,
∴……10分
学校 班级 姓名 座号 准考号: .
命题学校: 长乐一中 命题教师: 葛凤清 复核教师: 吴丽娜
---------密………封…………装…………订………线----------
. .
2
0
y
x
x
22.(14分)
20.(12分)
21.(12分)
2
18.(12分)
19.(12分)
(1)
(2)y=cosx y =
y =
y=
C
同课章节目录
