【深中联考】2023学年深圳市深中第二次共同体考试数学试卷(PDF版,含答案)
文档属性
| 名称 | 【深中联考】2023学年深圳市深中第二次共同体考试数学试卷(PDF版,含答案) |  | |
| 格式 | |||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-24 09:46:06 | ||
图片预览


文档简介
深中第二次共同体考试
九年级数学试卷
1. 答题前,务必将自己的姓名、学号等填写在答题卷规定的位置上。
2. 考生必须在答题卷上按规定作答:凡在试卷、草稿纸上作答的,其答案一律无效。
3. 全卷共 6 页,考试时间 90 分钟,满分 100 分。
第一部分 选择题
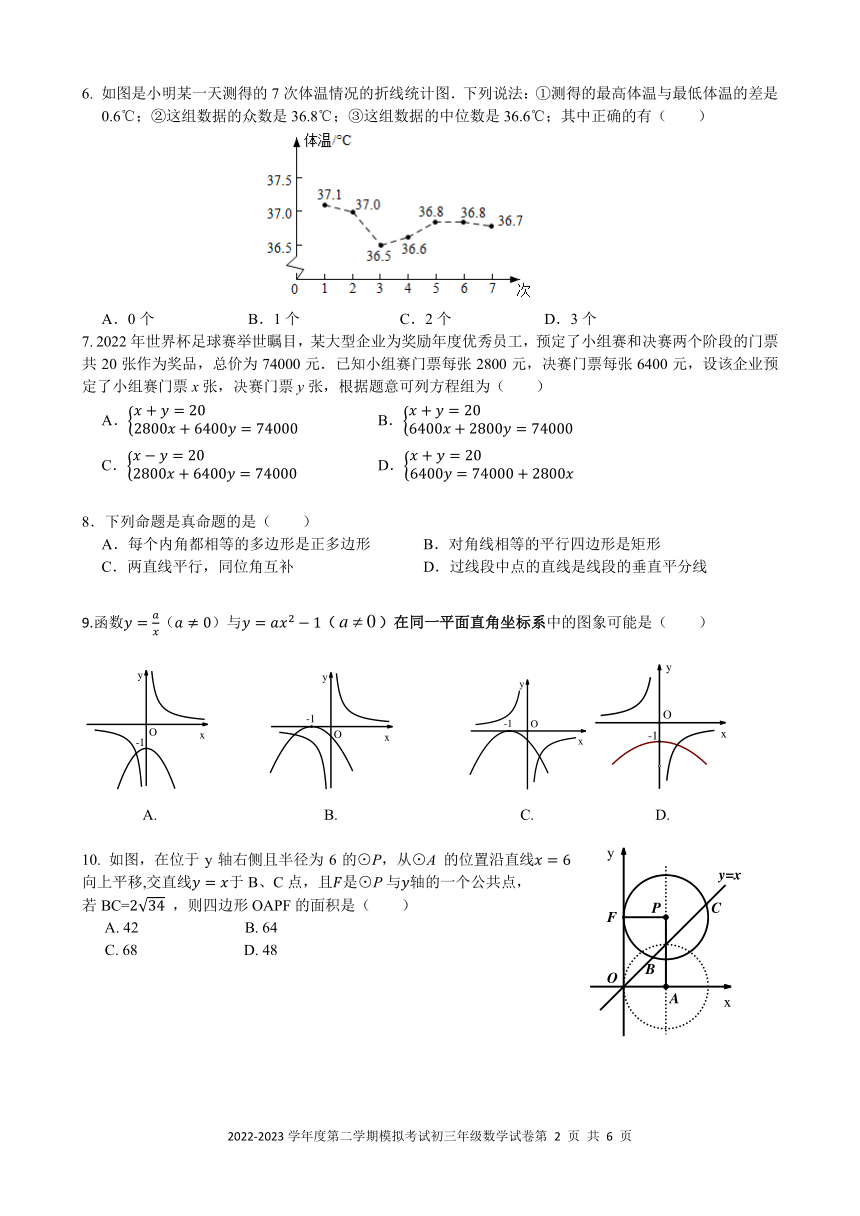
一. 选择题(本大题共 10 小题,每小题 3 分,共 30 分,每小题有四个选项,其中只有一个是正确的)
3
1.比较实数 0, √8,2, 1.7的大小,其中最小的实数为( )
3
A.0 B. √8 C.2 D. 1.7
2.作为我国核电走向世界的“国家名片”,“华龙一号”是当前核电市场接受度最高的三代核电机型之一,
是我国核电企业研发设计的具有完全自主知识产权的三代压水堆核电创新成果,中核集团“华龙一号”
示范工程全面建成后,每台机组年发电能力近 200 亿千瓦时.200 亿用科学记数法表示为( )
A.2×102 B.2×109 C.2×1010 D.2×1011
3. 下列运算正确的是( )
1
A. (√2023 + √23)(√2023 √23) = 2000 B. = 2 √5
√5 2
C. ( 3) = 4 4 D. ( 1) 1 = 1
4.如图,直线 l1∥l2,直线 AB 分别交 l1,l2 于点 A,B,∠MAB=120°,以点 B 为圆心,BA 长为半径画
弧,若在弧上存在点 C 使∠ACB=20°,则∠1 的度数是( )
A.80° B.75°
C.70° D.60°
5.通过小颖和小明的对话,我们可以判断他们共同搭的几何体是( )
A. B. C. D.
2022-2023 学年度第二学期模拟考试初三年级数学试卷第 1 页 共 6 页
6. 如图是小明某一天测得的 7 次体温情况的折线统计图.下列说法:①测得的最高体温与最低体温的差是
0.6℃;②这组数据的众数是 36.8℃;③这组数据的中位数是 36.6℃;其中正确的有( )
A.0 个 B.1 个 C.2 个 D.3 个
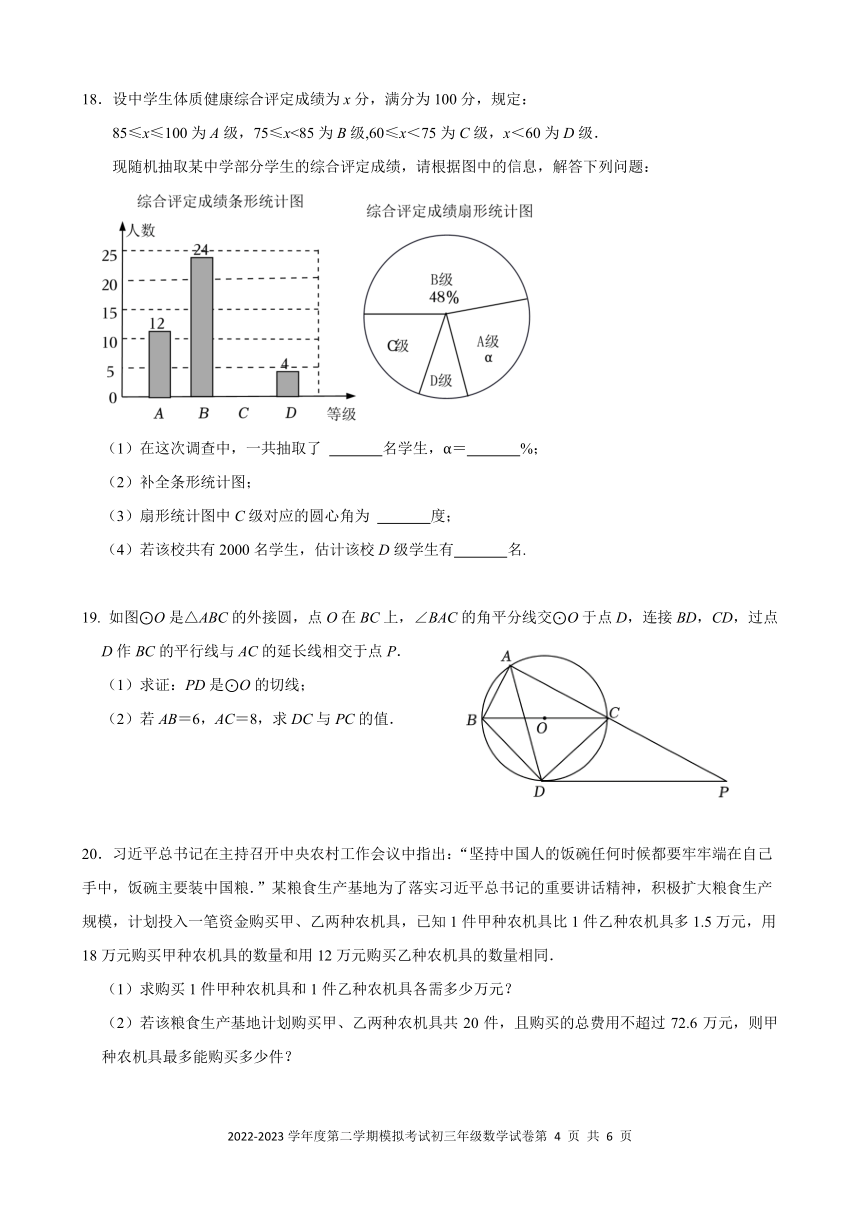
7. 2022 年世界杯足球赛举世瞩目,某大型企业为奖励年度优秀员工,预定了小组赛和决赛两个阶段的门票
共 20 张作为奖品,总价为 74000 元.已知小组赛门票每张 2800 元,决赛门票每张 6400 元,设该企业预
定了小组赛门票 x 张,决赛门票 y 张,根据题意可列方程组为( )
+ = 20 + = 20
A.{ B.{
2800 + 6400 = 74000 6400 + 2800 = 74000
= 20 + = 20
C.{ D.{
2800 + 6400 = 74000 6400 = 74000 + 2800
8.下列命题是真命题的是( )
A.每个内角都相等的多边形是正多边形 B.对角线相等的平行四边形是矩形
C.两直线平行,同位角互补 D.过线段中点的直线是线段的垂直平分线
9.函数 = ( ≠ 0)与 = 2 1(a 0)在同一平面直角坐标系中的图象可能是( )
y
y y
y
-1 O-1 O
O x O x -1 x
-1 x
A. B. C. D.
10. 如图,在位于 y 轴右侧且半径为 6 的⊙P,从⊙A 的位置沿直线 = 6 y
y=x
向上平移,交直线 = 于 B、C 点,且 是⊙P 与 轴的一个公共点,
若 BC=2√34 ,则四边形 OAPF 的面积是( ) P C
F
A. 42 B. 64
C. 68 D. 48
B
O
A x
2022-2023 学年度第二学期模拟考试初三年级数学试卷第 2 页 共 6 页
第二部分 非选择题
二.填空题(本大题共 5 小题,每小题 3 分,共 15 分)
11. 分解因式: 2 = .
12. 若 = 1关于 的一元二次方程 2 + + 23 = 0的解,则 + + 2000的值是 .
13. “二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.小文购买了
“二十四节气”主题邮票,他要将“立春”“立夏”“秋分”“大寒”四张邮票中的两张送给好朋友小乐.小
文将它们背面朝上放在桌面上(邮票背面完全相同),让小乐从中随机抽取一张(不放回),再从中随机
抽取一张,则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是 .
14. 如图,在平面直角坐标系中,点 P 是第一象限内的一点,其纵坐标为 2,过点 P 作 PQ⊥x 轴于点 Q,
以 PQ 为边向右侧作等边△PQM,若反比例函数 = ( >0, >0)的图象经过点 P 和点 M,则 k 的值
为 .
A
D
E
C B
第 14 题图 第 15 题图
15.如图,在△ABC 中,点 E 在边 AC 上,EC=EB,∠C=2∠ABE,AD⊥ BE 交 BE 的延长线于点 D,若
AC=22,BD=16,则 = .
三.解答题(本大题共 7 小题,其中第 16 题 5 分,第 17 题 6 分,第 18 题 8 分,第 19 题 8 分,第 20 题
8 分,第 21 题 10 分,第 22 题 10 分,共 55 分)
16.计算:|√3 2| 2tan60° + ( 2023)0 + √27.
a 3 6 2a + 6
17.先化简,再求值: ,其中a = 2 .
a a2 6a + 9 a2 9
2022-2023 学年度第二学期模拟考试初三年级数学试卷第 3 页 共 6 页
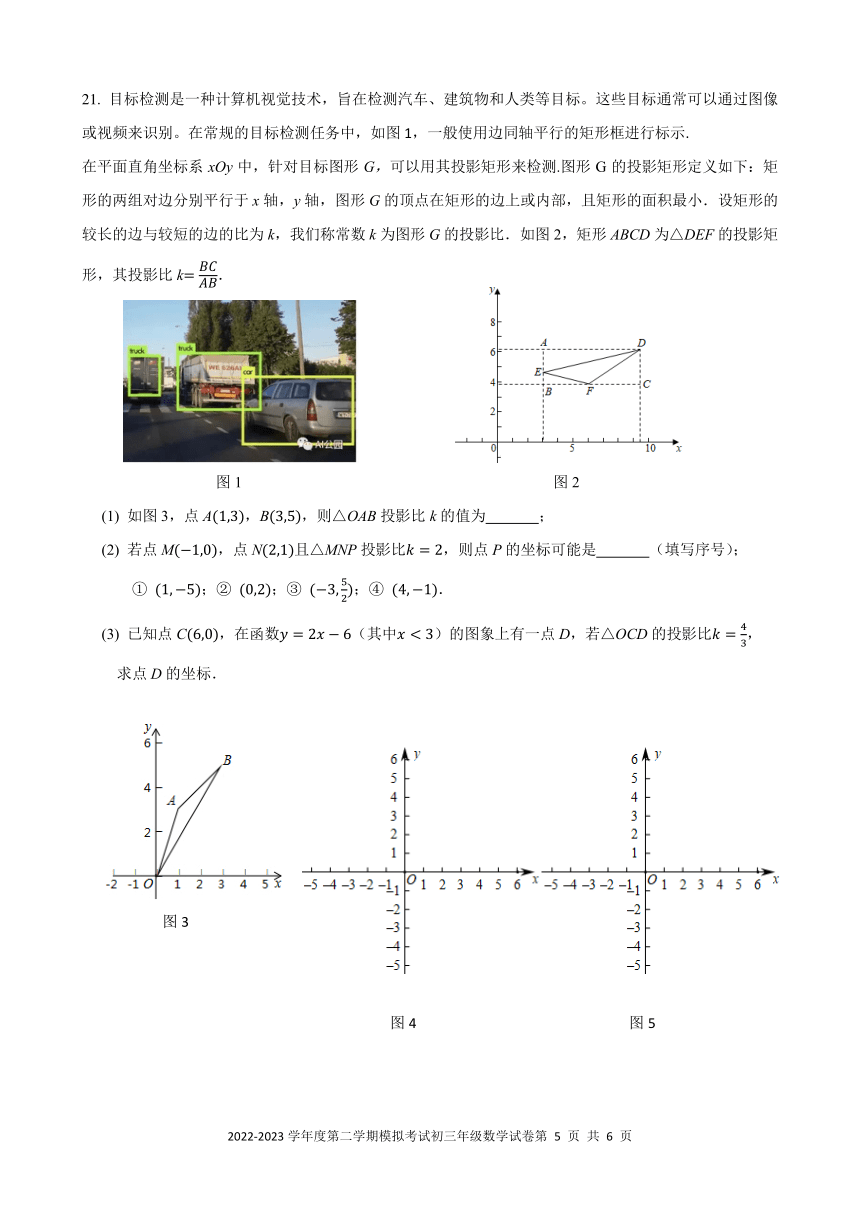
18.设中学生体质健康综合评定成绩为 x 分,满分为 100 分,规定:
85≤x≤100 为 A 级,75≤x<85 为 B 级,60≤x<75 为 C 级,x<60 为 D 级.
现随机抽取某中学部分学生的综合评定成绩,请根据图中的信息,解答下列问题:
(1)在这次调查中,一共抽取了 名学生,α= %;
(2)补全条形统计图;
(3)扇形统计图中 C 级对应的圆心角为 度;
(4)若该校共有 2000 名学生,估计该校 D 级学生有 名.
19. 如图⊙O 是△ABC 的外接圆,点 O 在 BC 上,∠BAC 的角平分线交⊙O 于点 D,连接 BD,CD,过点
D 作 BC 的平行线与 AC 的延长线相交于点 P.
(1)求证:PD 是⊙O 的切线;
(2)若 AB=6,AC=8,求 DC 与 PC 的值.
20.习近平总书记在主持召开中央农村工作会议中指出:“坚持中国人的饭碗任何时候都要牢牢端在自己
手中,饭碗主要装中国粮.”某粮食生产基地为了落实习近平总书记的重要讲话精神,积极扩大粮食生产
规模,计划投入一笔资金购买甲、乙两种农机具,已知 1 件甲种农机具比 1 件乙种农机具多 1.5 万元,用
18 万元购买甲种农机具的数量和用 12 万元购买乙种农机具的数量相同.
(1)求购买 1 件甲种农机具和 1 件乙种农机具各需多少万元?
(2)若该粮食生产基地计划购买甲、乙两种农机具共 20 件,且购买的总费用不超过 72.6 万元,则甲
种农机具最多能购买多少件?
2022-2023 学年度第二学期模拟考试初三年级数学试卷第 4 页 共 6 页
21. 目标检测是一种计算机视觉技术,旨在检测汽车、建筑物和人类等目标。这些目标通常可以通过图像
或视频来识别。在常规的目标检测任务中,如图 1,一般使用边同轴平行的矩形框进行标示.
在平面直角坐标系 xOy 中,针对目标图形 G,可以用其投影矩形来检测.图形 G 的投影矩形定义如下:矩
形的两组对边分别平行于 x 轴,y 轴,图形 G 的顶点在矩形的边上或内部,且矩形的面积最小.设矩形的
较长的边与较短的边的比为 k,我们称常数 k 为图形 G 的投影比.如图 2,矩形 ABCD 为△DEF 的投影矩
形,其投影比 k= .
图 1 图 2
(1) 如图 3,点 A(1,3),B(3,5),则△OAB 投影比 k 的值为 ;
(2) 若点 M( 1,0),点 N(2,1)且△MNP 投影比 = 2,则点 P 的坐标可能是 (填写序号);
5
① (1, 5);② (0,2);③ ( 3, );④ (4, 1).
2
4
(3) 已知点 C(6,0),在函数 = 2 6(其中 < 3)的图象上有一点 D,若△OCD 的投影比 = ,
3
求点 D 的坐标.
图 3
图 4 图 5
2022-2023 学年度第二学期模拟考试初三年级数学试卷第 5 页 共 6 页
22. 已知四边形 中, 为射线 上一点,过 作 // 交射线 于点 ,过 作 // 交射线
于点 .
(1)如图 1,四边形 是正方形,连结 交 于 ,则 与 的数量关系为 ;
若 = 3, = 7√2,, = (填数字);
图 1
(2)如图 2,四边形 是菱形,且直线 恰好经过点 ,连结 ,求 的值;
图 2
(3)如图 3,四边形 是菱形,连结 并延长与 交于点 ,若 是 的中点且△ 为等腰三
角形,直接写出:① 的值, ② ∠D的值.
图 3
2022-2023 学年度第二学期模拟考试初三年级数学试卷第 6 页 共 6 页
2022-2023 学年第二学期期中考试
九年级数学试卷答案
一. 选择题(本大题共 10 小题,每小题 3 分,共 30 分,每小题有四个选项,其中只有一个是正确的)
题号 1 2 3 4 5 6 7 8 9 10
答案 B C A A D C A B D D
二.填空题(本大题共 5 小题,每小题 3 分,共 15 分)
11..【 ( + 1)( 1)】 12.【2023】 13.【 】 14.【2√3】 15.【8√5】
三.解答题(本大题共 7 小题,其中第 16 题 5 分,第 17 题 6 分,第 18 题 8 分,第 19 题 8 分,第 20 题
8 分,第 21 题 10 分,第 22 题 10 分,共 55 分)
16.(5 分) 解:原式=2 √ 2√ +1+3√ …………4 分
=3.…………5 分
( + )
17. (6 分)解:原式= × …………3 分 ( ) ( )( + )
= …………4 分
( )
= = …………5 分
( )
当 = √ 时,原式= = √ …………6 分
√
18.(8 分)解:(1)50;24.…………每空 1 分,共 2 分
(2)补全条形统计图,如图所示:…………2 分
(3)答案为:72.…………2 分
(4)该校 D级学生有 160 名.…………2 分
1
19.(8 分)
解:【解答】(1)证明:如图 1,连接 OD,…………1 分
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴ = ,
∴∠BOD=∠COD=90°,…………2 分
∵BC∥PD,
∴∠ODP=∠BOD=90°,
∴OD⊥PD,…………3 分
∵OD是半径,
∴PD是⊙O的切线;…………4 分
(2)解:∵BC是⊙O的直径,
∴∠BAC=∠BDC=90°,
∵AB=6,AC=8,
∴ = √ + = ,
∵BD=CD,
∴ = = √ ,…………5 分
∵BC∥PD,
∴∠PDC=∠BCD.
∵∠BCD=∠BAD,
∴∠BAD=∠PDC,
∵∠ABD+∠ACD=180°,∠ACD+∠PCD=180°,
∴∠ABD=∠PCD,
∴△ABD∽△DCP,…………6 分
√
∴ = ,即 = ,…………7 分
√
∴ = .…………8 分
2
20.(8 分)
解:(1)设乙种农机具一件需 x万元,则甲种农机具一件需(x+1.5)万元,
根据题意得: = ,…………2 分
+ .
解得:x=3,………3 分
经检验:x=3 是方程的解且符合题意.
答:甲种农机具一件需 4.5 万元,乙种农机具一件需 3 万元,………4 分
(2)设甲种农机具最多能购买 a件,
则:4.5a+3(20﹣a)≤72.6,…………6 分
解得:a≤8.4,…………7 分
因为 a为正整数,
所以甲种农机具最多能购买 8 件.…………8 分
21. (10 分)
解:(1)△OAB投影比 k的值= .…………2 分
(2)共 4 分,每个序号 2 分
点 P的坐标可能是① ( , );③ ( , );
(3)共 4 分
∵点 D为函数 y=2x﹣6(其中 x<3)的图象上的点,
设点 D坐标为(x,2x﹣4)(x<3).
① 当 0≤x<3 时,
∴k= = ,解得 x= ,
∴D( , );…………2 分
② 当 x<0 时,
∴k= = ,解得 x= .
∴D( , );…………4 分
综上所述,点 D的坐标为( , )或( , );
3
22. (1)共 3 分,第一个空 1 分,第二个空 2 分,
= , =
(2)共 4 分
解:∵四边形 是菱形
∴ // , = ,∠ = ∠
∴∠ = ∠
∵ // , //
∴四边形 是平行四边形 ,∠ = ∠
∴ =
∵∠ = ∠
∴∠ = ∠
∴ =
∴ =
∴ ≌ ( ).………………..1 分
设 = , = ,则 = , = , =
∵ //
∴∠ = ∠ ,∠ = ∠ , =
∴ ∽ ( )…………………….2 分
∴ = ,则有 = ( > ),
+
√ +
解得 = ,…………………….3 分
√ +
∴ = = .…………………….4 分
(3)共 3 分,每个答案 1 分
① = √ + ,② ∠ = √ 或 ∠ = .
4
九年级数学试卷
1. 答题前,务必将自己的姓名、学号等填写在答题卷规定的位置上。
2. 考生必须在答题卷上按规定作答:凡在试卷、草稿纸上作答的,其答案一律无效。
3. 全卷共 6 页,考试时间 90 分钟,满分 100 分。
第一部分 选择题
一. 选择题(本大题共 10 小题,每小题 3 分,共 30 分,每小题有四个选项,其中只有一个是正确的)
3
1.比较实数 0, √8,2, 1.7的大小,其中最小的实数为( )
3
A.0 B. √8 C.2 D. 1.7
2.作为我国核电走向世界的“国家名片”,“华龙一号”是当前核电市场接受度最高的三代核电机型之一,
是我国核电企业研发设计的具有完全自主知识产权的三代压水堆核电创新成果,中核集团“华龙一号”
示范工程全面建成后,每台机组年发电能力近 200 亿千瓦时.200 亿用科学记数法表示为( )
A.2×102 B.2×109 C.2×1010 D.2×1011
3. 下列运算正确的是( )
1
A. (√2023 + √23)(√2023 √23) = 2000 B. = 2 √5
√5 2
C. ( 3) = 4 4 D. ( 1) 1 = 1
4.如图,直线 l1∥l2,直线 AB 分别交 l1,l2 于点 A,B,∠MAB=120°,以点 B 为圆心,BA 长为半径画
弧,若在弧上存在点 C 使∠ACB=20°,则∠1 的度数是( )
A.80° B.75°
C.70° D.60°
5.通过小颖和小明的对话,我们可以判断他们共同搭的几何体是( )
A. B. C. D.
2022-2023 学年度第二学期模拟考试初三年级数学试卷第 1 页 共 6 页
6. 如图是小明某一天测得的 7 次体温情况的折线统计图.下列说法:①测得的最高体温与最低体温的差是
0.6℃;②这组数据的众数是 36.8℃;③这组数据的中位数是 36.6℃;其中正确的有( )
A.0 个 B.1 个 C.2 个 D.3 个
7. 2022 年世界杯足球赛举世瞩目,某大型企业为奖励年度优秀员工,预定了小组赛和决赛两个阶段的门票
共 20 张作为奖品,总价为 74000 元.已知小组赛门票每张 2800 元,决赛门票每张 6400 元,设该企业预
定了小组赛门票 x 张,决赛门票 y 张,根据题意可列方程组为( )
+ = 20 + = 20
A.{ B.{
2800 + 6400 = 74000 6400 + 2800 = 74000
= 20 + = 20
C.{ D.{
2800 + 6400 = 74000 6400 = 74000 + 2800
8.下列命题是真命题的是( )
A.每个内角都相等的多边形是正多边形 B.对角线相等的平行四边形是矩形
C.两直线平行,同位角互补 D.过线段中点的直线是线段的垂直平分线
9.函数 = ( ≠ 0)与 = 2 1(a 0)在同一平面直角坐标系中的图象可能是( )
y
y y
y
-1 O-1 O
O x O x -1 x
-1 x
A. B. C. D.
10. 如图,在位于 y 轴右侧且半径为 6 的⊙P,从⊙A 的位置沿直线 = 6 y
y=x
向上平移,交直线 = 于 B、C 点,且 是⊙P 与 轴的一个公共点,
若 BC=2√34 ,则四边形 OAPF 的面积是( ) P C
F
A. 42 B. 64
C. 68 D. 48
B
O
A x
2022-2023 学年度第二学期模拟考试初三年级数学试卷第 2 页 共 6 页
第二部分 非选择题
二.填空题(本大题共 5 小题,每小题 3 分,共 15 分)
11. 分解因式: 2 = .
12. 若 = 1关于 的一元二次方程 2 + + 23 = 0的解,则 + + 2000的值是 .
13. “二十四节气”是中华上古农耕文明的智慧结晶,被国际气象界誉为“中国第五大发明”.小文购买了
“二十四节气”主题邮票,他要将“立春”“立夏”“秋分”“大寒”四张邮票中的两张送给好朋友小乐.小
文将它们背面朝上放在桌面上(邮票背面完全相同),让小乐从中随机抽取一张(不放回),再从中随机
抽取一张,则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是 .
14. 如图,在平面直角坐标系中,点 P 是第一象限内的一点,其纵坐标为 2,过点 P 作 PQ⊥x 轴于点 Q,
以 PQ 为边向右侧作等边△PQM,若反比例函数 = ( >0, >0)的图象经过点 P 和点 M,则 k 的值
为 .
A
D
E
C B
第 14 题图 第 15 题图
15.如图,在△ABC 中,点 E 在边 AC 上,EC=EB,∠C=2∠ABE,AD⊥ BE 交 BE 的延长线于点 D,若
AC=22,BD=16,则 = .
三.解答题(本大题共 7 小题,其中第 16 题 5 分,第 17 题 6 分,第 18 题 8 分,第 19 题 8 分,第 20 题
8 分,第 21 题 10 分,第 22 题 10 分,共 55 分)
16.计算:|√3 2| 2tan60° + ( 2023)0 + √27.
a 3 6 2a + 6
17.先化简,再求值: ,其中a = 2 .
a a2 6a + 9 a2 9
2022-2023 学年度第二学期模拟考试初三年级数学试卷第 3 页 共 6 页
18.设中学生体质健康综合评定成绩为 x 分,满分为 100 分,规定:
85≤x≤100 为 A 级,75≤x<85 为 B 级,60≤x<75 为 C 级,x<60 为 D 级.
现随机抽取某中学部分学生的综合评定成绩,请根据图中的信息,解答下列问题:
(1)在这次调查中,一共抽取了 名学生,α= %;
(2)补全条形统计图;
(3)扇形统计图中 C 级对应的圆心角为 度;
(4)若该校共有 2000 名学生,估计该校 D 级学生有 名.
19. 如图⊙O 是△ABC 的外接圆,点 O 在 BC 上,∠BAC 的角平分线交⊙O 于点 D,连接 BD,CD,过点
D 作 BC 的平行线与 AC 的延长线相交于点 P.
(1)求证:PD 是⊙O 的切线;
(2)若 AB=6,AC=8,求 DC 与 PC 的值.
20.习近平总书记在主持召开中央农村工作会议中指出:“坚持中国人的饭碗任何时候都要牢牢端在自己
手中,饭碗主要装中国粮.”某粮食生产基地为了落实习近平总书记的重要讲话精神,积极扩大粮食生产
规模,计划投入一笔资金购买甲、乙两种农机具,已知 1 件甲种农机具比 1 件乙种农机具多 1.5 万元,用
18 万元购买甲种农机具的数量和用 12 万元购买乙种农机具的数量相同.
(1)求购买 1 件甲种农机具和 1 件乙种农机具各需多少万元?
(2)若该粮食生产基地计划购买甲、乙两种农机具共 20 件,且购买的总费用不超过 72.6 万元,则甲
种农机具最多能购买多少件?
2022-2023 学年度第二学期模拟考试初三年级数学试卷第 4 页 共 6 页
21. 目标检测是一种计算机视觉技术,旨在检测汽车、建筑物和人类等目标。这些目标通常可以通过图像
或视频来识别。在常规的目标检测任务中,如图 1,一般使用边同轴平行的矩形框进行标示.
在平面直角坐标系 xOy 中,针对目标图形 G,可以用其投影矩形来检测.图形 G 的投影矩形定义如下:矩
形的两组对边分别平行于 x 轴,y 轴,图形 G 的顶点在矩形的边上或内部,且矩形的面积最小.设矩形的
较长的边与较短的边的比为 k,我们称常数 k 为图形 G 的投影比.如图 2,矩形 ABCD 为△DEF 的投影矩
形,其投影比 k= .
图 1 图 2
(1) 如图 3,点 A(1,3),B(3,5),则△OAB 投影比 k 的值为 ;
(2) 若点 M( 1,0),点 N(2,1)且△MNP 投影比 = 2,则点 P 的坐标可能是 (填写序号);
5
① (1, 5);② (0,2);③ ( 3, );④ (4, 1).
2
4
(3) 已知点 C(6,0),在函数 = 2 6(其中 < 3)的图象上有一点 D,若△OCD 的投影比 = ,
3
求点 D 的坐标.
图 3
图 4 图 5
2022-2023 学年度第二学期模拟考试初三年级数学试卷第 5 页 共 6 页
22. 已知四边形 中, 为射线 上一点,过 作 // 交射线 于点 ,过 作 // 交射线
于点 .
(1)如图 1,四边形 是正方形,连结 交 于 ,则 与 的数量关系为 ;
若 = 3, = 7√2,, = (填数字);
图 1
(2)如图 2,四边形 是菱形,且直线 恰好经过点 ,连结 ,求 的值;
图 2
(3)如图 3,四边形 是菱形,连结 并延长与 交于点 ,若 是 的中点且△ 为等腰三
角形,直接写出:① 的值, ② ∠D的值.
图 3
2022-2023 学年度第二学期模拟考试初三年级数学试卷第 6 页 共 6 页
2022-2023 学年第二学期期中考试
九年级数学试卷答案
一. 选择题(本大题共 10 小题,每小题 3 分,共 30 分,每小题有四个选项,其中只有一个是正确的)
题号 1 2 3 4 5 6 7 8 9 10
答案 B C A A D C A B D D
二.填空题(本大题共 5 小题,每小题 3 分,共 15 分)
11..【 ( + 1)( 1)】 12.【2023】 13.【 】 14.【2√3】 15.【8√5】
三.解答题(本大题共 7 小题,其中第 16 题 5 分,第 17 题 6 分,第 18 题 8 分,第 19 题 8 分,第 20 题
8 分,第 21 题 10 分,第 22 题 10 分,共 55 分)
16.(5 分) 解:原式=2 √ 2√ +1+3√ …………4 分
=3.…………5 分
( + )
17. (6 分)解:原式= × …………3 分 ( ) ( )( + )
= …………4 分
( )
= = …………5 分
( )
当 = √ 时,原式= = √ …………6 分
√
18.(8 分)解:(1)50;24.…………每空 1 分,共 2 分
(2)补全条形统计图,如图所示:…………2 分
(3)答案为:72.…………2 分
(4)该校 D级学生有 160 名.…………2 分
1
19.(8 分)
解:【解答】(1)证明:如图 1,连接 OD,…………1 分
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴ = ,
∴∠BOD=∠COD=90°,…………2 分
∵BC∥PD,
∴∠ODP=∠BOD=90°,
∴OD⊥PD,…………3 分
∵OD是半径,
∴PD是⊙O的切线;…………4 分
(2)解:∵BC是⊙O的直径,
∴∠BAC=∠BDC=90°,
∵AB=6,AC=8,
∴ = √ + = ,
∵BD=CD,
∴ = = √ ,…………5 分
∵BC∥PD,
∴∠PDC=∠BCD.
∵∠BCD=∠BAD,
∴∠BAD=∠PDC,
∵∠ABD+∠ACD=180°,∠ACD+∠PCD=180°,
∴∠ABD=∠PCD,
∴△ABD∽△DCP,…………6 分
√
∴ = ,即 = ,…………7 分
√
∴ = .…………8 分
2
20.(8 分)
解:(1)设乙种农机具一件需 x万元,则甲种农机具一件需(x+1.5)万元,
根据题意得: = ,…………2 分
+ .
解得:x=3,………3 分
经检验:x=3 是方程的解且符合题意.
答:甲种农机具一件需 4.5 万元,乙种农机具一件需 3 万元,………4 分
(2)设甲种农机具最多能购买 a件,
则:4.5a+3(20﹣a)≤72.6,…………6 分
解得:a≤8.4,…………7 分
因为 a为正整数,
所以甲种农机具最多能购买 8 件.…………8 分
21. (10 分)
解:(1)△OAB投影比 k的值= .…………2 分
(2)共 4 分,每个序号 2 分
点 P的坐标可能是① ( , );③ ( , );
(3)共 4 分
∵点 D为函数 y=2x﹣6(其中 x<3)的图象上的点,
设点 D坐标为(x,2x﹣4)(x<3).
① 当 0≤x<3 时,
∴k= = ,解得 x= ,
∴D( , );…………2 分
② 当 x<0 时,
∴k= = ,解得 x= .
∴D( , );…………4 分
综上所述,点 D的坐标为( , )或( , );
3
22. (1)共 3 分,第一个空 1 分,第二个空 2 分,
= , =
(2)共 4 分
解:∵四边形 是菱形
∴ // , = ,∠ = ∠
∴∠ = ∠
∵ // , //
∴四边形 是平行四边形 ,∠ = ∠
∴ =
∵∠ = ∠
∴∠ = ∠
∴ =
∴ =
∴ ≌ ( ).………………..1 分
设 = , = ,则 = , = , =
∵ //
∴∠ = ∠ ,∠ = ∠ , =
∴ ∽ ( )…………………….2 分
∴ = ,则有 = ( > ),
+
√ +
解得 = ,…………………….3 分
√ +
∴ = = .…………………….4 分
(3)共 3 分,每个答案 1 分
① = √ + ,② ∠ = √ 或 ∠ = .
4
同课章节目录
