第一章 直角三角形的边角关系 单元复习练习题 (含答案) 2022-2023学年北师大版九年级数学下册
文档属性
| 名称 | 第一章 直角三角形的边角关系 单元复习练习题 (含答案) 2022-2023学年北师大版九年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 479.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-20 22:45:14 | ||
图片预览




文档简介
第一章 直角三角形的边角关系
一、单项选择题。
1.如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,则下列三角函数表示正确的是( )
A.sinA= B.cosA= C.tanA= D.tanB=
2.在如图所示的方格网中,△ABC的三个顶点都在格点上,则tan ∠ACB的值为( )
A. B. C. D.3
3.如图,在平面直角坐标系中,直线OA过点(2,1),则sin α的值是( )
A. B. C. D.2
4.如图,点P在第二象限,OP与x轴负半轴的夹角是α,且OP=10,tan α=,则点P的坐标是( )
A.(6,8) B.(-6,8) C.(-8,6) D.(-6,10)
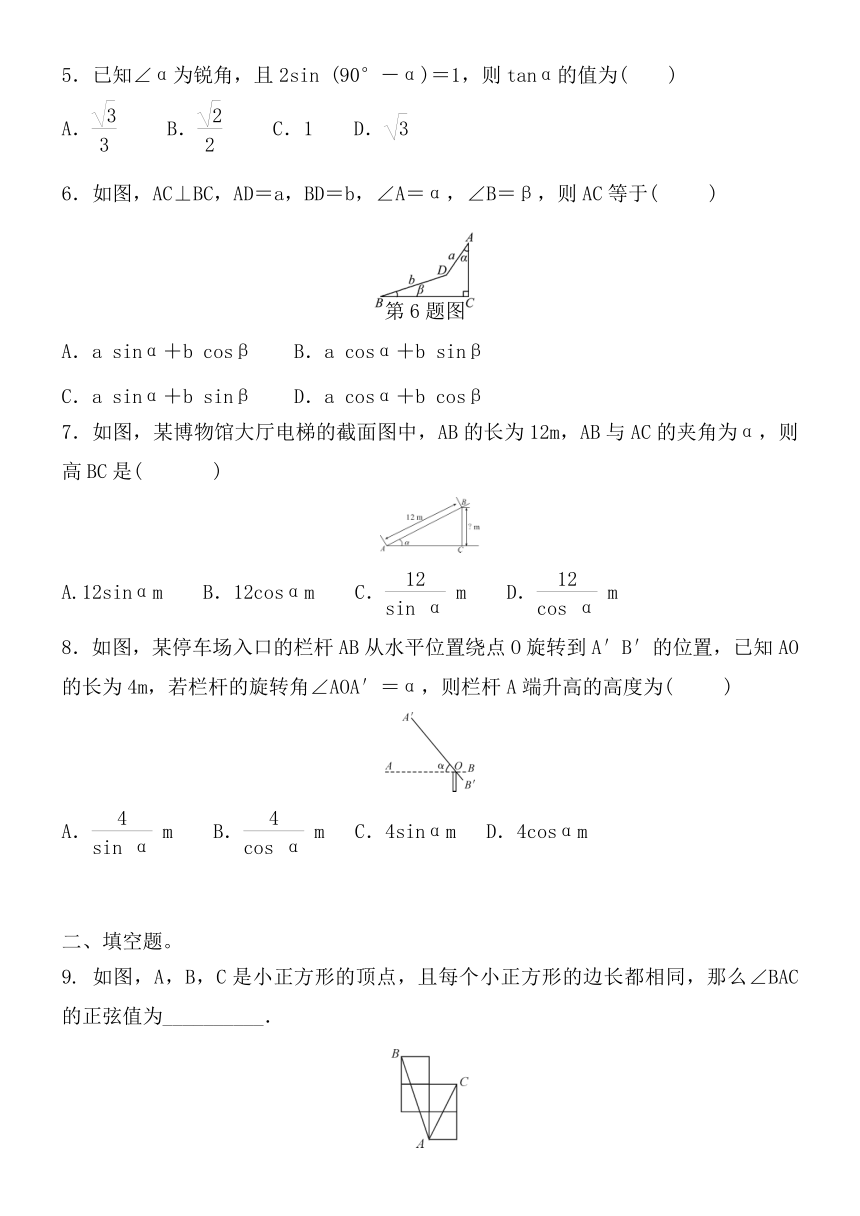
5.已知∠α为锐角,且2sin (90°-α)=1,则tanα的值为( )
A. B. C.1 D.
6.如图,AC⊥BC,AD=a,BD=b,∠A=α,∠B=β,则AC等于( )
A.a sinα+b cosβ B.a cosα+b sinβ
C.a sinα+b sinβ D.a cosα+b cosβ
7.如图,某博物馆大厅电梯的截面图中,AB的长为12m,AB与AC的夹角为α,则高BC是( )
A.12sinαm B.12cosαm C.m D.m
8.如图,某停车场入口的栏杆AB从水平位置绕点O旋转到A′B′的位置,已知AO的长为4m,若栏杆的旋转角∠AOA′=α,则栏杆A端升高的高度为( )
A.m B.m C.4sinαm D.4cosαm
二、填空题。
9. 如图,A,B,C是小正方形的顶点,且每个小正方形的边长都相同,那么∠BAC的正弦值为__________.
10. 2cos60°=__________.
11.已知∠α为锐角,且cos(90°-α)=,则∠α=____.
12. 如图,在△ABC中,AB=AC=5,BC=8.若∠BPC=∠BAC,则tan∠BPC的值为________.
13. 如图,在△ABC中,sin B=,tan C=2,AB=10,则AC的长为________.
14. 定义一种运算:sin(α+β)=sinαcosβ+cosαsinβ,sin(α-β)=sinαcosβ-cosαsinβ.例如:当α=45°,β=30°时,sin (45°+30°)=sin 45°cos30°+cos45°sin30°=×+×=,则sin15°的值为 ________________.
15. 某商场准备改善原有楼梯的安全性能,把坡角由37°减至30°,若已知原楼梯的长为5 m,则调整后的楼梯会加长约________m.(参考数据:sin 37°≈,cos 37°≈,tan 37°≈)
三、解答题。
16.计算:
(1)-tan260°;
(2)3tan30°-+cos 45°+.
17.如图,在锐角△ABC中,AB=15,BC=14,S△ABC=84,求tan C的值.
18.如图,在Rt△ABC中,∠ACB=90°,sin A=,点D是AB上的一点,DE⊥AC,垂足为E,若DE=2,DB=9,求:
(1)BC的长;
(2)cos∠BCD的值.
19.如图,为了测量河对岸A,B两点间的距离,数学兴趣小组在河岸南侧选定观测点C,测得A,B均在C的北偏东37°方向上,沿正东方向行走90m至观测点D,测得A在D的正北方向,B在D的北偏西53°方向上,求A,B两点间的距离(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).
20. 开封清明上河园是依照北宋著名画家张择端的《清明上河图》建造的,拂云阁是园内最高的建筑.某数学小组测量拂云阁DC的高度,如图,在A处用测角仪测得拂云阁顶端D的仰角为34°,沿AC方向前进15m到达B处,又测得拂云阁顶端D的仰角为45°.已知测角仪的高度为1.5m,测得点A,B与拂云阁DC的底部C在同一水平线上,求拂云阁DC的高度(结果精确到1m,参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67).
21. 如图,小敏在参观大风车时,想测一下风叶AB的长度.她首先通过C处的铭牌简介得知每个风车杆子BC的高度为98m,然后沿水平方向走到D处,再沿着斜坡DE走了35m到达E处,她站在E处,当风叶AB转到铅垂方向时测得点A的仰角为68°,当风叶AB转到水平方向A′B时测得点A′的仰角为45°,若斜坡DE的坡度i=1∶0.75,求风叶AB的长度(参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.50).
答案:
一、
1-8 AAABD BAC
二、
9.
10. 1
11. 45°
12.
13. 3
14.
15. 1
三、
16. 解:(1) 原式=-()2=+1-3=-2
(2) 原式=3×-+×+=-2+2+-1=2-1
17. 解:过点A作AD⊥BC于点D.∵S△ABC=BC·AD=84,∴·14AD=84,∴AD=12,∴BD===9,∴CD=BC-BD=14-9=5,∴在Rt△ADC中,tan C==
18. 解:(1)∵在Rt△DEA中,AD===3,∴AB=BD+AD=12,∴在Rt△ABC中,BC=AB·sin A=12×=8
(2)∵AC===4,AE===,∴CE=AC-AE=4-=3,∴CD===7,∴在Rt△CDE中,cos∠CDE==.又∵DE⊥AC,∴∠DEA=90°=∠ACB,∴DE∥BC,∴∠CDE=∠BCD,∴cos∠BCD=cos ∠CDE=
19. 解:根据题意可知∠A=37°,∠BDC=∠ADC-∠ADB=90°-53°=37°,∴∠CBD=∠A+∠ADB=37°+53°=90°,∴AB⊥BD,∴在Rt△BCD中,∴BD=CD·cos∠BDC=90cos37°≈90×0.80=72(m),∴在Rt△ABD中,AB=≈≈=96(m),∴A,B两点间的距离约为96m
20. 解:根据题意可知EF=AB=15m,延长EF交DC于点H,则CH=BF=AE=1.5m.设FH=x m,则EH=EF+FH=(15+x)m,在Rt△DFH中,DH=FH·tan ∠DFH=tan45°x=x(m).又∵在Rt△DHE中,tan ∠DEH=,∴=tan34°≈0.67,∴x≈30.5,∴DC=DH+CH=x+1.5≈30.5+1.5=32(m),∴拂云阁DC的高度约为32m
21. 解:过点E分别作EF⊥CD交CD的延长线于点F,EG⊥AC于点G,过点A′作A′H⊥EG交EG的延长线于点H,则四边形EFCG和四边形A′BGH为矩形,EF∶DF=i=1∶0.75,∴DF=EF,∴DE===EF=35m,∴EF=28m ,∴DF=EF=21m,∴A′H=BG=BC-CG=BC-EF=98-28=70(m),∴EH===70(m).设AB=A′B=xm,则EG=(70-x)m,AG=(70+x)m,∴在Rt△AEG中,==tan∠AEG=tan 68°≈2.5,解得x≈30,∴风叶AB的长度约为30m
一、单项选择题。
1.如图,在Rt△ABC中,∠C=90°,AB=13,AC=5,则下列三角函数表示正确的是( )
A.sinA= B.cosA= C.tanA= D.tanB=
2.在如图所示的方格网中,△ABC的三个顶点都在格点上,则tan ∠ACB的值为( )
A. B. C. D.3
3.如图,在平面直角坐标系中,直线OA过点(2,1),则sin α的值是( )
A. B. C. D.2
4.如图,点P在第二象限,OP与x轴负半轴的夹角是α,且OP=10,tan α=,则点P的坐标是( )
A.(6,8) B.(-6,8) C.(-8,6) D.(-6,10)
5.已知∠α为锐角,且2sin (90°-α)=1,则tanα的值为( )
A. B. C.1 D.
6.如图,AC⊥BC,AD=a,BD=b,∠A=α,∠B=β,则AC等于( )
A.a sinα+b cosβ B.a cosα+b sinβ
C.a sinα+b sinβ D.a cosα+b cosβ
7.如图,某博物馆大厅电梯的截面图中,AB的长为12m,AB与AC的夹角为α,则高BC是( )
A.12sinαm B.12cosαm C.m D.m
8.如图,某停车场入口的栏杆AB从水平位置绕点O旋转到A′B′的位置,已知AO的长为4m,若栏杆的旋转角∠AOA′=α,则栏杆A端升高的高度为( )
A.m B.m C.4sinαm D.4cosαm
二、填空题。
9. 如图,A,B,C是小正方形的顶点,且每个小正方形的边长都相同,那么∠BAC的正弦值为__________.
10. 2cos60°=__________.
11.已知∠α为锐角,且cos(90°-α)=,则∠α=____.
12. 如图,在△ABC中,AB=AC=5,BC=8.若∠BPC=∠BAC,则tan∠BPC的值为________.
13. 如图,在△ABC中,sin B=,tan C=2,AB=10,则AC的长为________.
14. 定义一种运算:sin(α+β)=sinαcosβ+cosαsinβ,sin(α-β)=sinαcosβ-cosαsinβ.例如:当α=45°,β=30°时,sin (45°+30°)=sin 45°cos30°+cos45°sin30°=×+×=,则sin15°的值为 ________________.
15. 某商场准备改善原有楼梯的安全性能,把坡角由37°减至30°,若已知原楼梯的长为5 m,则调整后的楼梯会加长约________m.(参考数据:sin 37°≈,cos 37°≈,tan 37°≈)
三、解答题。
16.计算:
(1)-tan260°;
(2)3tan30°-+cos 45°+.
17.如图,在锐角△ABC中,AB=15,BC=14,S△ABC=84,求tan C的值.
18.如图,在Rt△ABC中,∠ACB=90°,sin A=,点D是AB上的一点,DE⊥AC,垂足为E,若DE=2,DB=9,求:
(1)BC的长;
(2)cos∠BCD的值.
19.如图,为了测量河对岸A,B两点间的距离,数学兴趣小组在河岸南侧选定观测点C,测得A,B均在C的北偏东37°方向上,沿正东方向行走90m至观测点D,测得A在D的正北方向,B在D的北偏西53°方向上,求A,B两点间的距离(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75).
20. 开封清明上河园是依照北宋著名画家张择端的《清明上河图》建造的,拂云阁是园内最高的建筑.某数学小组测量拂云阁DC的高度,如图,在A处用测角仪测得拂云阁顶端D的仰角为34°,沿AC方向前进15m到达B处,又测得拂云阁顶端D的仰角为45°.已知测角仪的高度为1.5m,测得点A,B与拂云阁DC的底部C在同一水平线上,求拂云阁DC的高度(结果精确到1m,参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67).
21. 如图,小敏在参观大风车时,想测一下风叶AB的长度.她首先通过C处的铭牌简介得知每个风车杆子BC的高度为98m,然后沿水平方向走到D处,再沿着斜坡DE走了35m到达E处,她站在E处,当风叶AB转到铅垂方向时测得点A的仰角为68°,当风叶AB转到水平方向A′B时测得点A′的仰角为45°,若斜坡DE的坡度i=1∶0.75,求风叶AB的长度(参考数据:sin68°≈0.93,cos68°≈0.37,tan68°≈2.50).
答案:
一、
1-8 AAABD BAC
二、
9.
10. 1
11. 45°
12.
13. 3
14.
15. 1
三、
16. 解:(1) 原式=-()2=+1-3=-2
(2) 原式=3×-+×+=-2+2+-1=2-1
17. 解:过点A作AD⊥BC于点D.∵S△ABC=BC·AD=84,∴·14AD=84,∴AD=12,∴BD===9,∴CD=BC-BD=14-9=5,∴在Rt△ADC中,tan C==
18. 解:(1)∵在Rt△DEA中,AD===3,∴AB=BD+AD=12,∴在Rt△ABC中,BC=AB·sin A=12×=8
(2)∵AC===4,AE===,∴CE=AC-AE=4-=3,∴CD===7,∴在Rt△CDE中,cos∠CDE==.又∵DE⊥AC,∴∠DEA=90°=∠ACB,∴DE∥BC,∴∠CDE=∠BCD,∴cos∠BCD=cos ∠CDE=
19. 解:根据题意可知∠A=37°,∠BDC=∠ADC-∠ADB=90°-53°=37°,∴∠CBD=∠A+∠ADB=37°+53°=90°,∴AB⊥BD,∴在Rt△BCD中,∴BD=CD·cos∠BDC=90cos37°≈90×0.80=72(m),∴在Rt△ABD中,AB=≈≈=96(m),∴A,B两点间的距离约为96m
20. 解:根据题意可知EF=AB=15m,延长EF交DC于点H,则CH=BF=AE=1.5m.设FH=x m,则EH=EF+FH=(15+x)m,在Rt△DFH中,DH=FH·tan ∠DFH=tan45°x=x(m).又∵在Rt△DHE中,tan ∠DEH=,∴=tan34°≈0.67,∴x≈30.5,∴DC=DH+CH=x+1.5≈30.5+1.5=32(m),∴拂云阁DC的高度约为32m
21. 解:过点E分别作EF⊥CD交CD的延长线于点F,EG⊥AC于点G,过点A′作A′H⊥EG交EG的延长线于点H,则四边形EFCG和四边形A′BGH为矩形,EF∶DF=i=1∶0.75,∴DF=EF,∴DE===EF=35m,∴EF=28m ,∴DF=EF=21m,∴A′H=BG=BC-CG=BC-EF=98-28=70(m),∴EH===70(m).设AB=A′B=xm,则EG=(70-x)m,AG=(70+x)m,∴在Rt△AEG中,==tan∠AEG=tan 68°≈2.5,解得x≈30,∴风叶AB的长度约为30m
