四川省雅安市汉源县第一中学2022-2023学年九年级下学期第三次月考数学试卷(含简单答案)
文档属性
| 名称 | 四川省雅安市汉源县第一中学2022-2023学年九年级下学期第三次月考数学试卷(含简单答案) |  | |
| 格式 | docx | ||
| 文件大小 | 554.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-24 15:33:13 | ||
图片预览



文档简介
四川省雅安市汉源县第一中学2022-2023学年九年级下学期第三次月考数学试卷
(本卷满分100分,考试时间90分钟)
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题(本大题共12小题,每个题3分,共36分;在每小题给出的四个选项中,只有一个是符号题目要求的)
1.若抛物线y=x2-2x-1与x轴的一个交点坐标为(m,0),则代数式2m2-4m+2017的值为( )
A.2019 B.2018 C.2017 D.2015
2.下列天气预报中的图标,其中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.平面直角坐标系中,点关于原点对称的点的坐标是( )
A. B. C. D.
4.冬日的某个下午,小芳和爸爸正在阳光下散步,爸爸身高,他在地面上的影长为.若小芳高,则她的影长为( )
A.1.5m B.2.4m C.1.8m D.2m
5.(2015鄂州)在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2015B2015C2015D2015的边长是( )
A. B. C. D.
6.如图,抛物线与x轴交于点,其对称轴为直线,结合图象给出下列结论:
①;
②;
③当时,y随x的增大而增大;
④关于x的一元二次方程有一个实数根.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
7.将下面的某一点向下平移1个单位后,它在函数y=x2+2x﹣3的图象上,这个点是( )
A.(1,1) B.(2,﹣3) C.(1,﹣3) D.(2,﹣1)
8.如图为二次函数 y=ax2+bx+c 的图象,在下列说法中:①ac<0;②方程ax2+bx+c=0 的根是x1=﹣1,x2=3;③a+b+c>0;④当 x>1 时,y 随 x 的增大而增大;⑤2a﹣b=0⑥b2﹣4ac>0.下列结论一定成立的是( )
A.①②④⑥ B.①②③⑤ C.②③④⑤⑥ D.①②③④⑤⑥
9.已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0;②a-b+c<0;③2a=b;④4a+2b+c>0;⑤若点(-2,y1)和(-,y2)在该图象上,则y1>y2. 其中正确的结论个数是 ( )
A.1个 B.2个 C.3个 D.4个
10.在中,,点是边上的一动点,过点作交边于点,过点作交的延长线于点,分别以为对角线画矩形和矩形,则在从到的运动过程中,当矩形和矩形的面积和最小时,则的长度为( )
A. B. C.6 D.
11.如图平面直角坐标系中,矩形的顶点在轴负半轴上,边与轴交于点,连接轴,反比例函数的图象经过点及边上一点,若,则的值为( )
A.11 B.12 C.15 D.16
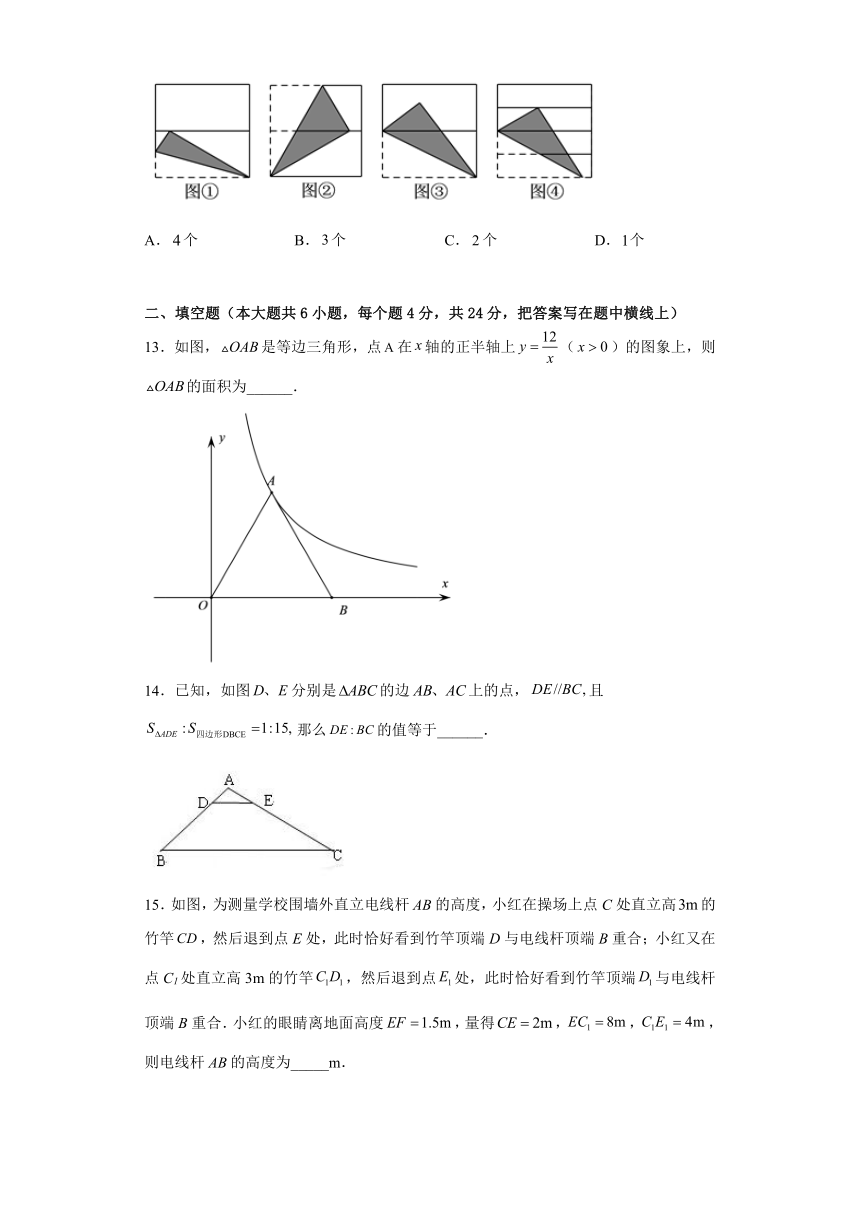
12.如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形(阴影部分),且它的一条直角边等于斜边的一半,这样的图形有( ).
A.个 B.个 C.个 D.个
二、填空题(本大题共6小题,每个题4分,共24分,把答案写在题中横线上)
13.如图,是等边三角形,点在轴的正半轴上()的图象上,则的面积为______.
14.已知,如图分别是的边上的点,且那么的值等于______.
15.如图,为测量学校围墙外直立电线杆的高度,小红在操场上点C处直立高的竹竿,然后退到点E处,此时恰好看到竹竿顶端D与电线杆顶端B重合;小红又在点C1处直立高3m的竹竿,然后退到点处,此时恰好看到竹竿顶端与电线杆顶端B重合.小红的眼睛离地面高度,量得,,,则电线杆的高度为_____m.
16.如图,矩形中,,,点在边上,把沿翻折后,点落在处.若恰为等腰三角形,则的长为_____.
17.如图,正方形的边长为4,E为上一点,且,F为边上的一个动点,连接,将烧点E顺时什旋转60°得到,连接,则的最小值为______.
18.如图,E为正方形ABCD边CD上一点,DE=3,CE=1,F为直线BC上一点,直线DF与直线AE交于G,且DF=AE,则DG=_______.
三、解答题(本大题共6小题,前4题每题7分,最后两题各9分,共计46分。解答题写出必要计算过程。)
19.已知线段为线段,的比例中项,若,,则的值.
20.根据展开图画出物体的三视图,并求物体的表面积和体积.
21.如图,在平面直角坐标系中,△ABC的三个顶点都在格点上(每个小方格都是边长为一个单位长度的正方形).
(1)请画出△ABC关于原点对称的△A1B1C1;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2B2C2.
22.计算:;
23.如图,已知和,连接BD,CE,,.
(1)求证:.
(2)若,,设线段DB的延长线与线段EC的延长线交于点F,请直接写出的度数.
24.(1)计算:
(2)解方程:
25.为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子水平放置在离B(树底)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,求树AB的高度.
26.如图⑴,在△ABC中,∠C=90°,AC=8cm,BC=6cm. 点M由点B出发沿BA方向向点A匀速运动,同时点N由点A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s .连接MN,设运动时间为t(s)﹙0<t<4﹚,解答下列问题:
⑴设△AMN的面积为S,求S与t之间的函数关系式,并求出S的最大值;
⑵如图⑵,连接MC,将△MNC沿NC翻折,得到四边形MNPC,当四边形MNPC为菱形时,求t的值;
⑶当t的值为 ,△AMN是等腰三角形.
参考答案:
1.A
2.A
3.C
4.D
5.D
6.B
7.A
8.A
9.B
10.D
11.C
12.C
13.12
14.
15.10.5
16.2或
17.
18.或.
19.
20.画出三视图见解析;表面积为144π;体积为192π+π.
21.(1)无;(2)无
22.
23.(1)无;(2)
24.(1)4;(2).
25.树AB的高度为4.2米
26.(1), ;(2)t=;(3)或或
答案第1页,共2页
(本卷满分100分,考试时间90分钟)
学校:___________姓名:___________班级:___________考号:___________
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题(本大题共12小题,每个题3分,共36分;在每小题给出的四个选项中,只有一个是符号题目要求的)
1.若抛物线y=x2-2x-1与x轴的一个交点坐标为(m,0),则代数式2m2-4m+2017的值为( )
A.2019 B.2018 C.2017 D.2015
2.下列天气预报中的图标,其中既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
3.平面直角坐标系中,点关于原点对称的点的坐标是( )
A. B. C. D.
4.冬日的某个下午,小芳和爸爸正在阳光下散步,爸爸身高,他在地面上的影长为.若小芳高,则她的影长为( )
A.1.5m B.2.4m C.1.8m D.2m
5.(2015鄂州)在平面直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3、A3B3C3D3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2015B2015C2015D2015的边长是( )
A. B. C. D.
6.如图,抛物线与x轴交于点,其对称轴为直线,结合图象给出下列结论:
①;
②;
③当时,y随x的增大而增大;
④关于x的一元二次方程有一个实数根.
其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
7.将下面的某一点向下平移1个单位后,它在函数y=x2+2x﹣3的图象上,这个点是( )
A.(1,1) B.(2,﹣3) C.(1,﹣3) D.(2,﹣1)
8.如图为二次函数 y=ax2+bx+c 的图象,在下列说法中:①ac<0;②方程ax2+bx+c=0 的根是x1=﹣1,x2=3;③a+b+c>0;④当 x>1 时,y 随 x 的增大而增大;⑤2a﹣b=0⑥b2﹣4ac>0.下列结论一定成立的是( )
A.①②④⑥ B.①②③⑤ C.②③④⑤⑥ D.①②③④⑤⑥
9.已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①abc>0;②a-b+c<0;③2a=b;④4a+2b+c>0;⑤若点(-2,y1)和(-,y2)在该图象上,则y1>y2. 其中正确的结论个数是 ( )
A.1个 B.2个 C.3个 D.4个
10.在中,,点是边上的一动点,过点作交边于点,过点作交的延长线于点,分别以为对角线画矩形和矩形,则在从到的运动过程中,当矩形和矩形的面积和最小时,则的长度为( )
A. B. C.6 D.
11.如图平面直角坐标系中,矩形的顶点在轴负半轴上,边与轴交于点,连接轴,反比例函数的图象经过点及边上一点,若,则的值为( )
A.11 B.12 C.15 D.16
12.如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形(阴影部分),且它的一条直角边等于斜边的一半,这样的图形有( ).
A.个 B.个 C.个 D.个
二、填空题(本大题共6小题,每个题4分,共24分,把答案写在题中横线上)
13.如图,是等边三角形,点在轴的正半轴上()的图象上,则的面积为______.
14.已知,如图分别是的边上的点,且那么的值等于______.
15.如图,为测量学校围墙外直立电线杆的高度,小红在操场上点C处直立高的竹竿,然后退到点E处,此时恰好看到竹竿顶端D与电线杆顶端B重合;小红又在点C1处直立高3m的竹竿,然后退到点处,此时恰好看到竹竿顶端与电线杆顶端B重合.小红的眼睛离地面高度,量得,,,则电线杆的高度为_____m.
16.如图,矩形中,,,点在边上,把沿翻折后,点落在处.若恰为等腰三角形,则的长为_____.
17.如图,正方形的边长为4,E为上一点,且,F为边上的一个动点,连接,将烧点E顺时什旋转60°得到,连接,则的最小值为______.
18.如图,E为正方形ABCD边CD上一点,DE=3,CE=1,F为直线BC上一点,直线DF与直线AE交于G,且DF=AE,则DG=_______.
三、解答题(本大题共6小题,前4题每题7分,最后两题各9分,共计46分。解答题写出必要计算过程。)
19.已知线段为线段,的比例中项,若,,则的值.
20.根据展开图画出物体的三视图,并求物体的表面积和体积.
21.如图,在平面直角坐标系中,△ABC的三个顶点都在格点上(每个小方格都是边长为一个单位长度的正方形).
(1)请画出△ABC关于原点对称的△A1B1C1;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2B2C2.
22.计算:;
23.如图,已知和,连接BD,CE,,.
(1)求证:.
(2)若,,设线段DB的延长线与线段EC的延长线交于点F,请直接写出的度数.
24.(1)计算:
(2)解方程:
25.为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组做了如下探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子水平放置在离B(树底)8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,求树AB的高度.
26.如图⑴,在△ABC中,∠C=90°,AC=8cm,BC=6cm. 点M由点B出发沿BA方向向点A匀速运动,同时点N由点A出发沿AC方向向点C匀速运动,它们的速度均为2cm/s .连接MN,设运动时间为t(s)﹙0<t<4﹚,解答下列问题:
⑴设△AMN的面积为S,求S与t之间的函数关系式,并求出S的最大值;
⑵如图⑵,连接MC,将△MNC沿NC翻折,得到四边形MNPC,当四边形MNPC为菱形时,求t的值;
⑶当t的值为 ,△AMN是等腰三角形.
参考答案:
1.A
2.A
3.C
4.D
5.D
6.B
7.A
8.A
9.B
10.D
11.C
12.C
13.12
14.
15.10.5
16.2或
17.
18.或.
19.
20.画出三视图见解析;表面积为144π;体积为192π+π.
21.(1)无;(2)无
22.
23.(1)无;(2)
24.(1)4;(2).
25.树AB的高度为4.2米
26.(1), ;(2)t=;(3)或或
答案第1页,共2页
同课章节目录
