北师大版八年级数学上册试题 1.1 探索勾股定理(含答案)
文档属性
| 名称 | 北师大版八年级数学上册试题 1.1 探索勾股定理(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 473.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-04 15:46:12 | ||
图片预览




文档简介
1.1 探索勾股定理
一、选择题
1.已知一个直角三角形的两条直角边长分别为6和8,则第三边长的平方是( )
A.36 B.64 C.100 D.100或28
2.一直角三角形的两直角边长为6和8,则斜边长为( )
A.10 B.13 C.7 D.14
3.如图,为了求出分别位于池塘两岸的点A与点B的距离,小亮在点C处立一标杆,使是直角,测得AC的长为85m,BC的长为75m,则点A与点B的距离是( )
A.20m B.40m C.30m D.50m
4.如图是一张直角三角形的纸片,两直角边AC=6 cm、BC=8 cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
A.4 cm B.4.75 cm C.6 cm D.5cm
5.如图,有一块长方形花圃,有少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了( )m的路,却踩伤了花草.
A.5 B.4 C.3 D.2
6.在中,斜边,则等于( )
A.5 B.25 C.50 D.100
7.如图,中,,以它的各边为边向外作三个正方形,面积分别为、、,已知,,( ).
A.90 B.100 C.110 D.120
8. 在中,若,,,则点C到直线AB的距离为( )
A.3 B.4 C.5 D.2.4
9. 如图,中,,将沿DE翻折,使点A与点B重合,则CE的长为( )
A. B.2 C. D.
二、填空题
1.在中,,
(1)如果a=3,b=4,则c=____;
(2)如果a=6,b=8,则c=____;
(3)如果a=5,b=12,则c=____;
(4)如果a=15,b=20,则c=____
2.如图,在2×2的网格中,线段AB的端点均在网格线的交点上,若每个小正方形的边长均为1,则线段AB的长为_________________.
3.直角三角形一直角边为12cm,斜边长为13cm,则它的面积为______
4.小颖从学校出发向南走了150m,接着向东走了80m到达书店,则学校与书店的距离是__m.
5.如图,用四个全等的直角三角形拼成如图一个大正方形ABCD和一个小正方形EFGH,这就是著名的“赵爽弦图”.在2002年北京召开的国际数学家大会就用这个弦图作为会 标.若AB=10,AF=8,则小正方形EFGH的面积为__________
6.如图,数字代表所在正方形的面积,则A所代表的正方形的面积为_________.
7. 如图.在中,,平分,于E,若,则的长为________.
8.《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”其意思为:今有一门,高比宽多6尺8寸,门对角线距离恰好为1丈.问门高、宽各是多少?(1丈=10尺,1尺=10寸)如图, 设门高为尺,根据题意,可列方程为________.
三、解答题
1.设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1)已知,求b;
(2)已知,求c;
(3)已知,求a.
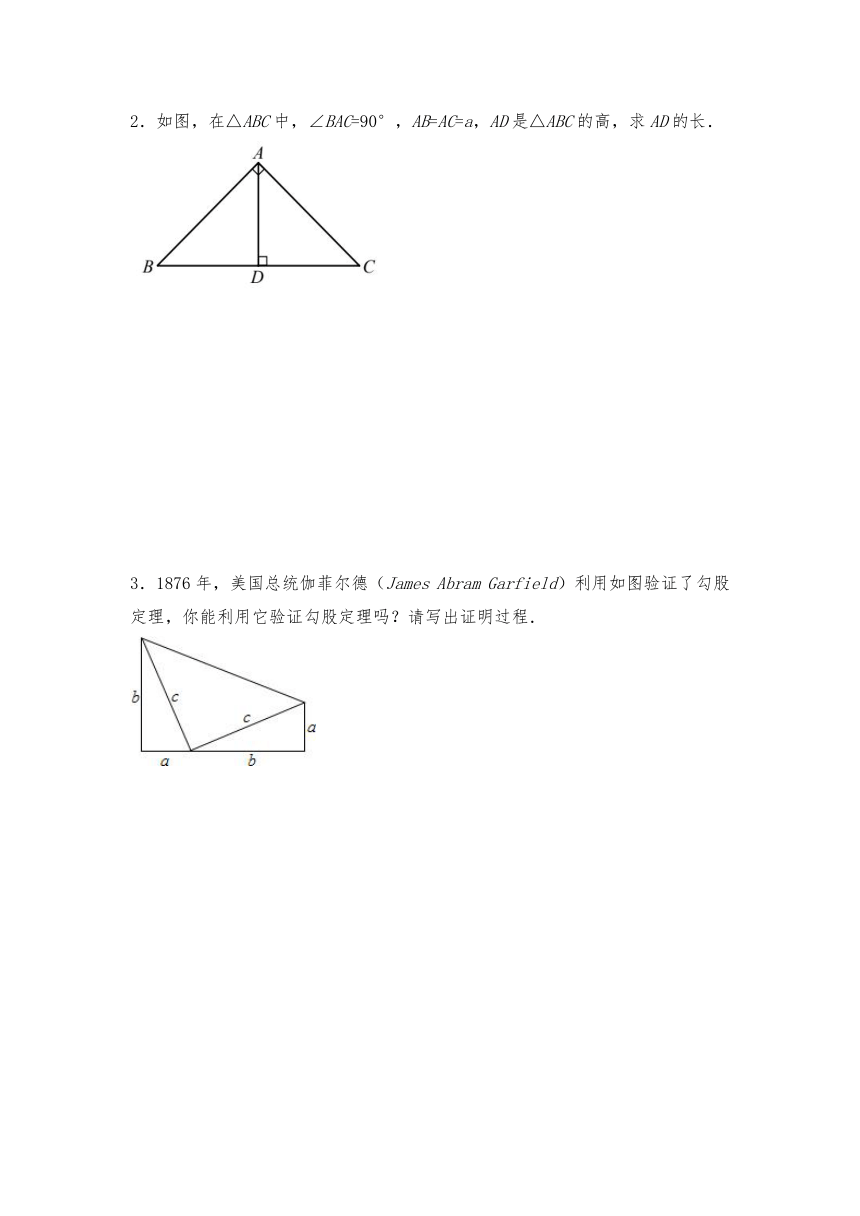
2.如图,在△ABC中,∠BAC=90°,AB=AC=a,AD是△ABC的高,求AD的长.
3.1876年,美国总统伽菲尔德(James Abram Garfield)利用如图验证了勾股定理,你能利用它验证勾股定理吗?请写出证明过程.
4.如图,有一架秋千,当他静止时,踏板离地的垂直高度,将他往前推送(水平距离)时,秋千的踏板离地的垂直高度,秋千的绳索始终拉得很直,求绳索的长度.
5.根据勾股定理知识迁移,完成下列应用.
(1)如图1,分别以直角三角形的三边为直径向外侧作半圆,则它们的面积,,之间满足的等量关系是________;
(2)应用:如图2,直角三角形的两条直角边长分别为a,b,斜边长为c,分别以三边为直径作半圆,若,,求图中阴影部分的面积.
6.如图①,美丽的弦图,蕴含着四个全等的直角三角形.
(1)弦图中包含了一大,一小两个正方形,已知每个直角三角形较长的直角边为a,较短的直角边为b,斜边长为c,结合图①,试验证勾股定理.
(2)如图②,将这四个直角三角形紧密地拼接,形成飞镖状,已知外围轮廓(粗线)的周长为24,,求该飞镖状图案的面积.
(3)如图③,将八个全等的直角三角形紧密地拼接,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为,若,求.
答案
一、选择题
C.A.B.D.B.B. B. D.D.
二、填空题
1. 5 10 13 25
2.. 3.30. 4.170. 5.4. 6.100.
7..8..
三、解答题
1.解:(1)直角三角形的两条直角边长分别为和,斜边长为,,,
;
(2)直角三角形的两条直角边长分别为和,斜边长为,,,
;
(3)直角三角形的两条直角边长分别为和,斜边长为,,,
.
2.解:∵在△ABC中,∠BAC=90°,AB=AC=a,
∴BC=,
∵AD是△ABC的高,
∴S△ABC=×AB×AC=×BC×AD,
即×a×a=×a×AD,
解得AD=a.
故AD的长为a.
3.解:能,理由如下:
∵直角梯形的面积等于三个直角三角形的面积之和,
∴ (a+b)(a+b)=2×ab+c2,
∴(a+b)(a+b)=2ab+c2,
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2.
4.解:设秋千的绳索长为,则,
,
在中,
,即,
解得,
答:绳索的长度是.
5.(1)如图,设直角三角形的三边长分别为,则
故答案为:
(2)设直角三角形为S4,直角三角形三边为直径的半圆的面积,,
∵直角边a=3,斜边c=5
∴,则
∴阴影部分的面积S=S1+S2+S4-S3=S4=6
6.(1)
法一:,
另一方面,,
即,则.
法二:
另一方面,
∴
整理得:
(2)
,
设,依题意有
解得
.
故该飞镖状图案的面积是24.
(3)
将四边形MTKN的面积设为x,将其余八个全等的三角形一个的面积设为y,
∵正方形ABCD,正方形EFGH,正方形MNKT的面积分别为,且,
∴,
∴,
∴,
∴.
一、选择题
1.已知一个直角三角形的两条直角边长分别为6和8,则第三边长的平方是( )
A.36 B.64 C.100 D.100或28
2.一直角三角形的两直角边长为6和8,则斜边长为( )
A.10 B.13 C.7 D.14
3.如图,为了求出分别位于池塘两岸的点A与点B的距离,小亮在点C处立一标杆,使是直角,测得AC的长为85m,BC的长为75m,则点A与点B的距离是( )
A.20m B.40m C.30m D.50m
4.如图是一张直角三角形的纸片,两直角边AC=6 cm、BC=8 cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
A.4 cm B.4.75 cm C.6 cm D.5cm
5.如图,有一块长方形花圃,有少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了( )m的路,却踩伤了花草.
A.5 B.4 C.3 D.2
6.在中,斜边,则等于( )
A.5 B.25 C.50 D.100
7.如图,中,,以它的各边为边向外作三个正方形,面积分别为、、,已知,,( ).
A.90 B.100 C.110 D.120
8. 在中,若,,,则点C到直线AB的距离为( )
A.3 B.4 C.5 D.2.4
9. 如图,中,,将沿DE翻折,使点A与点B重合,则CE的长为( )
A. B.2 C. D.
二、填空题
1.在中,,
(1)如果a=3,b=4,则c=____;
(2)如果a=6,b=8,则c=____;
(3)如果a=5,b=12,则c=____;
(4)如果a=15,b=20,则c=____
2.如图,在2×2的网格中,线段AB的端点均在网格线的交点上,若每个小正方形的边长均为1,则线段AB的长为_________________.
3.直角三角形一直角边为12cm,斜边长为13cm,则它的面积为______
4.小颖从学校出发向南走了150m,接着向东走了80m到达书店,则学校与书店的距离是__m.
5.如图,用四个全等的直角三角形拼成如图一个大正方形ABCD和一个小正方形EFGH,这就是著名的“赵爽弦图”.在2002年北京召开的国际数学家大会就用这个弦图作为会 标.若AB=10,AF=8,则小正方形EFGH的面积为__________
6.如图,数字代表所在正方形的面积,则A所代表的正方形的面积为_________.
7. 如图.在中,,平分,于E,若,则的长为________.
8.《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”其意思为:今有一门,高比宽多6尺8寸,门对角线距离恰好为1丈.问门高、宽各是多少?(1丈=10尺,1尺=10寸)如图, 设门高为尺,根据题意,可列方程为________.
三、解答题
1.设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1)已知,求b;
(2)已知,求c;
(3)已知,求a.
2.如图,在△ABC中,∠BAC=90°,AB=AC=a,AD是△ABC的高,求AD的长.
3.1876年,美国总统伽菲尔德(James Abram Garfield)利用如图验证了勾股定理,你能利用它验证勾股定理吗?请写出证明过程.
4.如图,有一架秋千,当他静止时,踏板离地的垂直高度,将他往前推送(水平距离)时,秋千的踏板离地的垂直高度,秋千的绳索始终拉得很直,求绳索的长度.
5.根据勾股定理知识迁移,完成下列应用.
(1)如图1,分别以直角三角形的三边为直径向外侧作半圆,则它们的面积,,之间满足的等量关系是________;
(2)应用:如图2,直角三角形的两条直角边长分别为a,b,斜边长为c,分别以三边为直径作半圆,若,,求图中阴影部分的面积.
6.如图①,美丽的弦图,蕴含着四个全等的直角三角形.
(1)弦图中包含了一大,一小两个正方形,已知每个直角三角形较长的直角边为a,较短的直角边为b,斜边长为c,结合图①,试验证勾股定理.
(2)如图②,将这四个直角三角形紧密地拼接,形成飞镖状,已知外围轮廓(粗线)的周长为24,,求该飞镖状图案的面积.
(3)如图③,将八个全等的直角三角形紧密地拼接,记图中正方形ABCD,正方形EFGH,正方形MNKT的面积分别为,若,求.
答案
一、选择题
C.A.B.D.B.B. B. D.D.
二、填空题
1. 5 10 13 25
2.. 3.30. 4.170. 5.4. 6.100.
7..8..
三、解答题
1.解:(1)直角三角形的两条直角边长分别为和,斜边长为,,,
;
(2)直角三角形的两条直角边长分别为和,斜边长为,,,
;
(3)直角三角形的两条直角边长分别为和,斜边长为,,,
.
2.解:∵在△ABC中,∠BAC=90°,AB=AC=a,
∴BC=,
∵AD是△ABC的高,
∴S△ABC=×AB×AC=×BC×AD,
即×a×a=×a×AD,
解得AD=a.
故AD的长为a.
3.解:能,理由如下:
∵直角梯形的面积等于三个直角三角形的面积之和,
∴ (a+b)(a+b)=2×ab+c2,
∴(a+b)(a+b)=2ab+c2,
∴a2+2ab+b2=2ab+c2,
∴a2+b2=c2.
4.解:设秋千的绳索长为,则,
,
在中,
,即,
解得,
答:绳索的长度是.
5.(1)如图,设直角三角形的三边长分别为,则
故答案为:
(2)设直角三角形为S4,直角三角形三边为直径的半圆的面积,,
∵直角边a=3,斜边c=5
∴,则
∴阴影部分的面积S=S1+S2+S4-S3=S4=6
6.(1)
法一:,
另一方面,,
即,则.
法二:
另一方面,
∴
整理得:
(2)
,
设,依题意有
解得
.
故该飞镖状图案的面积是24.
(3)
将四边形MTKN的面积设为x,将其余八个全等的三角形一个的面积设为y,
∵正方形ABCD,正方形EFGH,正方形MNKT的面积分别为,且,
∴,
∴,
∴,
∴.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
