北师大版九年级数学下册第二章 二次函数(二次函数及确定其表达式)试题(含答案)
文档属性
| 名称 | 北师大版九年级数学下册第二章 二次函数(二次函数及确定其表达式)试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 205.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-06-30 13:15:01 | ||
图片预览




文档简介
二次函数及确定其表达式
第一课时
一、单选题
1.下列函数解析式中,一定为二次函数的是( )
A. y=3x-1 B.y=ax2+bx+c C.s=2t2-2t+1 D.y=x2+
2.下列函数关系中,是二次函数的为( )
A.在弹性限度内,弹簧的长度y与所挂物体的质量x之间的关系.
B.距离一定时,火车行驶的时间t与速度v之间的关系
C.等边三角形的周长C与边长a之间的关系
D.圆的面积S与半径之间的关系
3.在二次函数y=﹣x2+5x﹣2中,a、b、c对应的值为( )
A.a=1,b=5,c=﹣2 B.a=﹣1,b=5,c=2
C.a=﹣1,b=5,c=﹣2 D.a=﹣1,b=﹣5,c=﹣2
4.已知函数是二次函数,则m的值为()
A.±2 B.2 C.-2 D.m为全体实数
5.函数 (a,b,c为常数)是二次函数的条件是( ).
A.或 B. C.且 D.
6.已知二次函数y=(a﹣1)x2﹣x+a2﹣1图象经过原点,则a的取值为( )
A.a=±1 B.a=1 C.a=﹣1 D.无法确定
7.抛物线经过点,,,则当时,y的值为( ).
A.6 B.1 C.-1 D.-6
8.已知抛物线经过和两点,则的值为( )
A. B. C. D.
9.已知二次函数y=ax2+4x+c,当x等于﹣2时,函数值是﹣1;当x=1时,函数值是5.则此二次函数的表达式为( )
A.y=2x2+4x﹣1 B.y=x2+4x﹣2
C.y=-2x2+4x+1 D.y=2x2+4x+1
10.对于y=ax2+bx+c,有以下四种说法,其中正确的是( )
A.当b=0时,二次函数是y=ax2+c B.当c=0时,二次函数是y=ax2+bx
C.当a=0时,一次函数是y=bx+c D.以上说法都不对
二、填空题
11.已知函数y=(m﹣2)x2+mx﹣3(m为常数).
(1)当m_______时,该函数为二次函数;
(2)当m_______时,该函数为一次函数.
12.下列函数①;②;③;④;⑤.其中是二次函数的是____________.
13.半径是2的圆,如果半径增加x时,增加的面积s与x之间的关系表达式为__________.
14.一般地,若两个自变量x,y之间的对应关系可以表示成 (a,b,c是常数,a≠0)的形式,则称y是x的______函数.其中,x是______,a为_______,叫做________;b为_______,bx叫做________;c为_______.
15.已知y=+2x﹣3是二次函数式,则m的值为 _____.
16.二次函数解析式通常有三种形式:①一般式______________________________;②顶点式______________________________;③双根式______________________________.
17.已知点在函数的图象上,则a等于______.
18.抛物线上部分点的横坐标x,纵坐标y的对应值如下表:
x 0 1 2 3 4
y 3 0 -1 0 3
则抛物线的解析式是______________.
三、解答题
19.某工厂计划为一批长方体形状的产品表面涂上油漆,长方体的长和宽相等,高比长多.
(1)长方体的长和宽用表示,长方体的表面积的表达式是什么?
(2)如果涂漆每平方米所需要的费用是5元,油漆每个长方体所需费用用y(元)表示,那么y的表达式是什么?
20.一个二次函数.
(1)求k的值.
(2)求当x=3时,y的值?
21.已知函数.
(1)若这个函数是一次函数,求的值
(2)若这个函数是二次函数,求的取值范围.
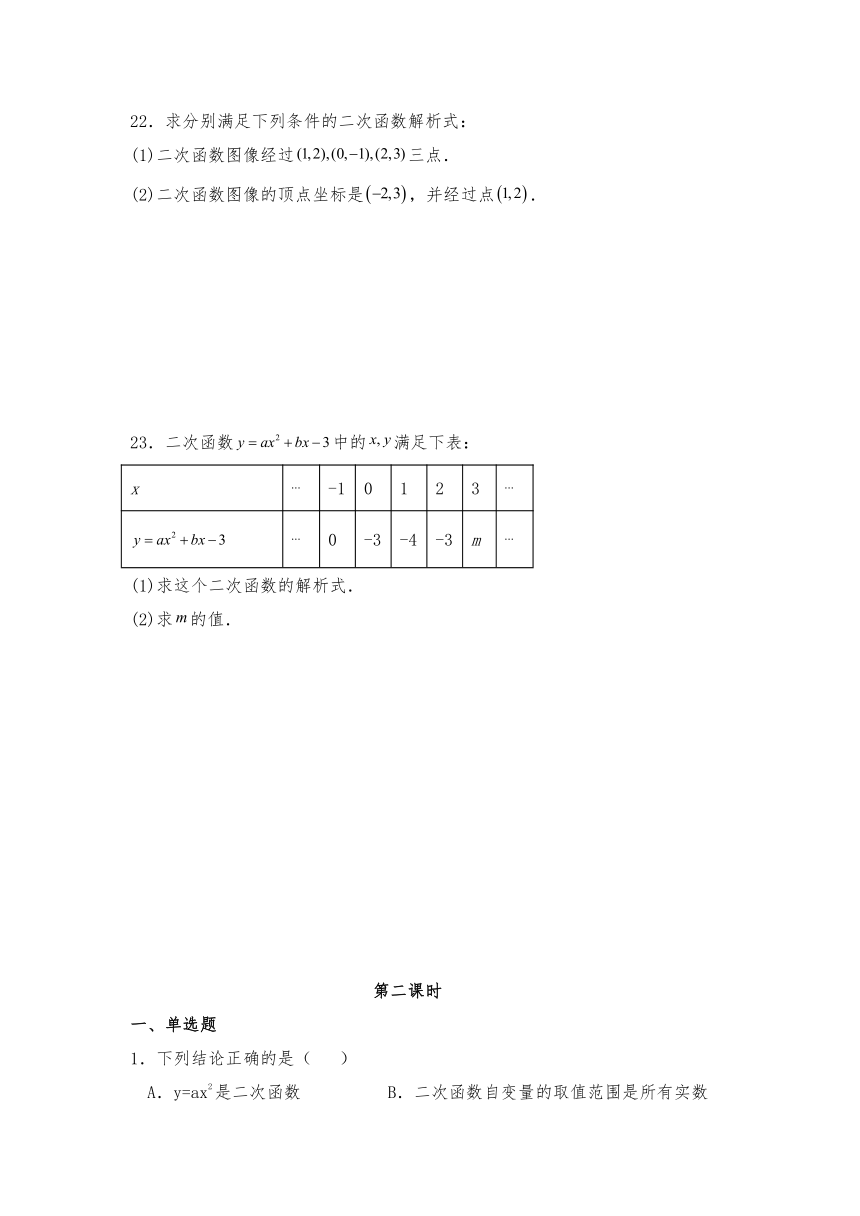
22.求分别满足下列条件的二次函数解析式:
(1)二次函数图像经过三点.
(2)二次函数图像的顶点坐标是,并经过点.
23.二次函数中的满足下表:
x -1 0 1 2 3
0 -3 -4 -3 m
(1)求这个二次函数的解析式.
(2)求的值.
第二课时
一、单选题
1.下列结论正确的是( )
A.y=ax2是二次函数 B.二次函数自变量的取值范围是所有实数
C.二次方程是二次函数的特例 D.二次函数的取值范围是非零实数
2.二次函数y=x2+px+q中,若p+q=0,则它的图象必经过下列四点中( )
A.(-1,1) B.(1,-1) C.(-1,-1) D.(1,1)
3.已知二次函数y=﹣+bx+c的图象经过(﹣1,0)与(5,0)两点,且关于x的方程﹣x2+bx+c+d=0有两个根,其中一个根是6,则d的值为( )
A.5 B.7 C.12 D.﹣7
4.某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出下面的表格:
由于粗心,他算错了其中一个y值,则这个错误的数值是( )
A.-11 B.-2 C.1 D.-5
5.设y=y1﹣y2,y1与x成正比例,y2与x2成正比例,则y与x的函数关系是( )
A.正比例函数 B.一次函数
C.二次函数 D.以上均不正确
6.已知函数y=ax2+bx+c,其中a,b,c可在0,1,2,3,4五个数中取值,则不同的二次函数的个数共有( )
A.125个 B.100个 C.48个 D.10个
二、填空题
7.已知二次函数,如果当x=-1时y=2,那么当x=2时,y=_____.
8.点是二次函数图像上一点,则的值为__________
9.一个二次函数,当自变量时,函数值,且过点和点,则这个二次函数的解析式为________________.
10.抛物线过两点,与y轴的交点为,则抛物线的解析式__________.
11.定义:由a,b构造的二次函数叫做一次函数y=ax+b的“滋生函数”,一次函数y=ax+b叫做二次函数的“本源函数”(a,b为常数,且).若一次函数y=ax+b的“滋生函数”是,那么二次函数的“本源函数”是______.
三、解答题
12.(1)已知二次函数的图象经过与两点,求这个二次函数的表达式;
(2)请更换第(1)题中的部分已知条件,重新设计一个求二次函数表达式的题目,使所求得的二次函数与第(1)题相同.
13.已知y=y1+y2,其中y1与x﹣3成正比例,y2与x2+1成正比例,且当x=0时,y=﹣4,当x=﹣1时,y=﹣6.
(1)求y与x的函数关系式;
(2)判断点A(1,﹣4)是否在此函数图象上,并说明理由.
第一课时答案
一、单选题
C.D.C.C.B.C.D.C.A.D.
二、填空题
11. ≠2 =2
12.②④.
13.S=πx2+4πx.
14. 二 二次 自变量 二次项系数 二次项 一次项系数 一次项 常数项
15.-1.
16.,,.
17.1.
18..
三、解答题
19.解:(1)
;
(2).
20.解:(1)依题意有,
解得:k=2,
∴k的值为2;
(2)把k=2代入函数解析式中得:,
当x=3时,y=14,
∴y的值为14.
21.解:(1)由题意得,解得;
(2)由题意得,,解得且.
22.(1)
解:设二次函数的解析式为,将代入得,
,
解得,
二次函数的解析式为;
(2)
设二次函数的解析式为,将点代入得,
,
解得,
二次函数的解析式为.
23.(1)
解:根据表格可知对称轴为直线,且时,即顶点为,
设解析式为,当时,,
即,
解得,
∴这个二次函数的解析式为:,
即
(2)
解:∵对称轴为直线,
∴当与时的函数值相等,
∴
第二课时答案
一、单选题
B.D.B.D.C.B
二、填空题
7.8.
8.6.
9..
10..
11..
三、解答题
12.解:(1)把(1,1)与(2,3)分别代入y=x2+bx+c得
,解得;
所以二次函数的解析式为;
(2)改为:二次函数y=x2+bx+c的图象经过(0,1)与(1,3)两点,求这个二次函数的表达式.
把(0,1)与(1,3)分别代入y=x2+bx+c得
,解得
所以二次函数的解析式为.
13.解:(1)设y1=k1(x﹣3),y2=k(x2+1),
∵y=y1+y2,
∴y=k1(x﹣3)+k(x2+1),
把x=0,y=﹣4;x=﹣1,y=﹣6分别代入y=k1(x﹣3)+k(x2+1),
得:,
解得:,
则y=x﹣3﹣(x2+1)=﹣x2+x﹣4;
(2)点A(1,﹣4)在此函数图象上,理由如下:
把x=1代入y=﹣x2+x﹣4,
得:y=﹣1+1﹣4=﹣4,
∴A(1,﹣4)在此函数图象上.
第一课时
一、单选题
1.下列函数解析式中,一定为二次函数的是( )
A. y=3x-1 B.y=ax2+bx+c C.s=2t2-2t+1 D.y=x2+
2.下列函数关系中,是二次函数的为( )
A.在弹性限度内,弹簧的长度y与所挂物体的质量x之间的关系.
B.距离一定时,火车行驶的时间t与速度v之间的关系
C.等边三角形的周长C与边长a之间的关系
D.圆的面积S与半径之间的关系
3.在二次函数y=﹣x2+5x﹣2中,a、b、c对应的值为( )
A.a=1,b=5,c=﹣2 B.a=﹣1,b=5,c=2
C.a=﹣1,b=5,c=﹣2 D.a=﹣1,b=﹣5,c=﹣2
4.已知函数是二次函数,则m的值为()
A.±2 B.2 C.-2 D.m为全体实数
5.函数 (a,b,c为常数)是二次函数的条件是( ).
A.或 B. C.且 D.
6.已知二次函数y=(a﹣1)x2﹣x+a2﹣1图象经过原点,则a的取值为( )
A.a=±1 B.a=1 C.a=﹣1 D.无法确定
7.抛物线经过点,,,则当时,y的值为( ).
A.6 B.1 C.-1 D.-6
8.已知抛物线经过和两点,则的值为( )
A. B. C. D.
9.已知二次函数y=ax2+4x+c,当x等于﹣2时,函数值是﹣1;当x=1时,函数值是5.则此二次函数的表达式为( )
A.y=2x2+4x﹣1 B.y=x2+4x﹣2
C.y=-2x2+4x+1 D.y=2x2+4x+1
10.对于y=ax2+bx+c,有以下四种说法,其中正确的是( )
A.当b=0时,二次函数是y=ax2+c B.当c=0时,二次函数是y=ax2+bx
C.当a=0时,一次函数是y=bx+c D.以上说法都不对
二、填空题
11.已知函数y=(m﹣2)x2+mx﹣3(m为常数).
(1)当m_______时,该函数为二次函数;
(2)当m_______时,该函数为一次函数.
12.下列函数①;②;③;④;⑤.其中是二次函数的是____________.
13.半径是2的圆,如果半径增加x时,增加的面积s与x之间的关系表达式为__________.
14.一般地,若两个自变量x,y之间的对应关系可以表示成 (a,b,c是常数,a≠0)的形式,则称y是x的______函数.其中,x是______,a为_______,叫做________;b为_______,bx叫做________;c为_______.
15.已知y=+2x﹣3是二次函数式,则m的值为 _____.
16.二次函数解析式通常有三种形式:①一般式______________________________;②顶点式______________________________;③双根式______________________________.
17.已知点在函数的图象上,则a等于______.
18.抛物线上部分点的横坐标x,纵坐标y的对应值如下表:
x 0 1 2 3 4
y 3 0 -1 0 3
则抛物线的解析式是______________.
三、解答题
19.某工厂计划为一批长方体形状的产品表面涂上油漆,长方体的长和宽相等,高比长多.
(1)长方体的长和宽用表示,长方体的表面积的表达式是什么?
(2)如果涂漆每平方米所需要的费用是5元,油漆每个长方体所需费用用y(元)表示,那么y的表达式是什么?
20.一个二次函数.
(1)求k的值.
(2)求当x=3时,y的值?
21.已知函数.
(1)若这个函数是一次函数,求的值
(2)若这个函数是二次函数,求的取值范围.
22.求分别满足下列条件的二次函数解析式:
(1)二次函数图像经过三点.
(2)二次函数图像的顶点坐标是,并经过点.
23.二次函数中的满足下表:
x -1 0 1 2 3
0 -3 -4 -3 m
(1)求这个二次函数的解析式.
(2)求的值.
第二课时
一、单选题
1.下列结论正确的是( )
A.y=ax2是二次函数 B.二次函数自变量的取值范围是所有实数
C.二次方程是二次函数的特例 D.二次函数的取值范围是非零实数
2.二次函数y=x2+px+q中,若p+q=0,则它的图象必经过下列四点中( )
A.(-1,1) B.(1,-1) C.(-1,-1) D.(1,1)
3.已知二次函数y=﹣+bx+c的图象经过(﹣1,0)与(5,0)两点,且关于x的方程﹣x2+bx+c+d=0有两个根,其中一个根是6,则d的值为( )
A.5 B.7 C.12 D.﹣7
4.某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出下面的表格:
由于粗心,他算错了其中一个y值,则这个错误的数值是( )
A.-11 B.-2 C.1 D.-5
5.设y=y1﹣y2,y1与x成正比例,y2与x2成正比例,则y与x的函数关系是( )
A.正比例函数 B.一次函数
C.二次函数 D.以上均不正确
6.已知函数y=ax2+bx+c,其中a,b,c可在0,1,2,3,4五个数中取值,则不同的二次函数的个数共有( )
A.125个 B.100个 C.48个 D.10个
二、填空题
7.已知二次函数,如果当x=-1时y=2,那么当x=2时,y=_____.
8.点是二次函数图像上一点,则的值为__________
9.一个二次函数,当自变量时,函数值,且过点和点,则这个二次函数的解析式为________________.
10.抛物线过两点,与y轴的交点为,则抛物线的解析式__________.
11.定义:由a,b构造的二次函数叫做一次函数y=ax+b的“滋生函数”,一次函数y=ax+b叫做二次函数的“本源函数”(a,b为常数,且).若一次函数y=ax+b的“滋生函数”是,那么二次函数的“本源函数”是______.
三、解答题
12.(1)已知二次函数的图象经过与两点,求这个二次函数的表达式;
(2)请更换第(1)题中的部分已知条件,重新设计一个求二次函数表达式的题目,使所求得的二次函数与第(1)题相同.
13.已知y=y1+y2,其中y1与x﹣3成正比例,y2与x2+1成正比例,且当x=0时,y=﹣4,当x=﹣1时,y=﹣6.
(1)求y与x的函数关系式;
(2)判断点A(1,﹣4)是否在此函数图象上,并说明理由.
第一课时答案
一、单选题
C.D.C.C.B.C.D.C.A.D.
二、填空题
11. ≠2 =2
12.②④.
13.S=πx2+4πx.
14. 二 二次 自变量 二次项系数 二次项 一次项系数 一次项 常数项
15.-1.
16.,,.
17.1.
18..
三、解答题
19.解:(1)
;
(2).
20.解:(1)依题意有,
解得:k=2,
∴k的值为2;
(2)把k=2代入函数解析式中得:,
当x=3时,y=14,
∴y的值为14.
21.解:(1)由题意得,解得;
(2)由题意得,,解得且.
22.(1)
解:设二次函数的解析式为,将代入得,
,
解得,
二次函数的解析式为;
(2)
设二次函数的解析式为,将点代入得,
,
解得,
二次函数的解析式为.
23.(1)
解:根据表格可知对称轴为直线,且时,即顶点为,
设解析式为,当时,,
即,
解得,
∴这个二次函数的解析式为:,
即
(2)
解:∵对称轴为直线,
∴当与时的函数值相等,
∴
第二课时答案
一、单选题
B.D.B.D.C.B
二、填空题
7.8.
8.6.
9..
10..
11..
三、解答题
12.解:(1)把(1,1)与(2,3)分别代入y=x2+bx+c得
,解得;
所以二次函数的解析式为;
(2)改为:二次函数y=x2+bx+c的图象经过(0,1)与(1,3)两点,求这个二次函数的表达式.
把(0,1)与(1,3)分别代入y=x2+bx+c得
,解得
所以二次函数的解析式为.
13.解:(1)设y1=k1(x﹣3),y2=k(x2+1),
∵y=y1+y2,
∴y=k1(x﹣3)+k(x2+1),
把x=0,y=﹣4;x=﹣1,y=﹣6分别代入y=k1(x﹣3)+k(x2+1),
得:,
解得:,
则y=x﹣3﹣(x2+1)=﹣x2+x﹣4;
(2)点A(1,﹣4)在此函数图象上,理由如下:
把x=1代入y=﹣x2+x﹣4,
得:y=﹣1+1﹣4=﹣4,
∴A(1,﹣4)在此函数图象上.
