北师大版数学八年级上册1.1 探索勾股定理提升练习题 (含解析)
文档属性
| 名称 | 北师大版数学八年级上册1.1 探索勾股定理提升练习题 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 254.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-07 10:12:18 | ||
图片预览



文档简介
1.1 探索勾股定理(提升题) 北师大版八年级上册
一.选择题
.如图,在Rt△BOD中,分别以BD,OD,BO为直径向外作三个半圆,其面积分别为S1,S2,S3,若S1=40,S3=18,则S2=( )
A.18 B.20 C.22 D.24
.勾股定理在《九章算术》中的表述是:“勾股术曰:勾股各自乘,并而开方除之,即弦”.即c=(a为勾,b为股,c为弦),若“勾”为2,“股”为3,则“弦”最接近的整数是( )
A.1 B.2 C.3 D.4
.点A、B、C在格点图中的位置如图所示,格点小正方形的边长为1,则点C到AB的距离是( )
A. B. C. D.
.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,在6×6的正方形网格图形ABCD中,M,N分别是AB,BC上的格点,BM=4,BN=2.若点P是这个网格图形中的格点,连结PM,PN,则所有满足∠MPN=45°的△PMN中,边PM的长的最大值是( )
A.4 B.6 C.2 D.3
.已知直角三角形两边的长为5和12,则此三角形的周长为( )
A.30 B.+17 C.+17或30 D.36
.已知3,4,m是一个直角三角形的三条边长,则实数m的相反数为( )
A.5 B.﹣5 C.5或 D.﹣5或﹣
.如图,这是用面积为18的四个全等的直角三角形拼成的“赵爽弦图”.如果大正方形的边长为9,那么小正方形的边长为( )
A.1 B.2 C.3 D.4
.如图,在Rt△ABC中,∠C=90°,AC=12,BC=18,DE是线段AB的垂直平分线,则BD的长为( )
A.8 B.10 C.13 D.15
.如图所示,在四边形ABCD中,∠B=∠D=90°,∠BAC=30°,∠CAD=45°,BC=4,点P是四边形ABCD边上的一个动点,若点P到AC的距离为2,则点P的位置有( )
A.1处 B.2处 C.3处 D.4处
.勾股定理被誉为“几何明珠”,如图是我国古代著名的“赵爽弦图”,它由4个全等的直角三角形拼成,已知大正方形面积为25,小正方形面积为1,若用a、b表示直角三角形的两直角边(a>b),则下列说法:①a2+b2=25,②a﹣b=1,③ab=12,④a+b=7.正确的是( )
A.①② B.①②③ C.①②④ D.①②③④
二.填空题
.若直角三角形的两边长分别为3,4,则该直角三角形的斜边长为 .
.如图,在Rt△ABC中,∠A=90°,AB=3,BC=5,BC的垂直平分线交AC于点D,垂足为点E,则AD= .
.已知Rt△ABC中,AB=8,BC=10,∠BAC=90°,则图中阴影部分面积为 .
.如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E,若AB=4,则CD= .
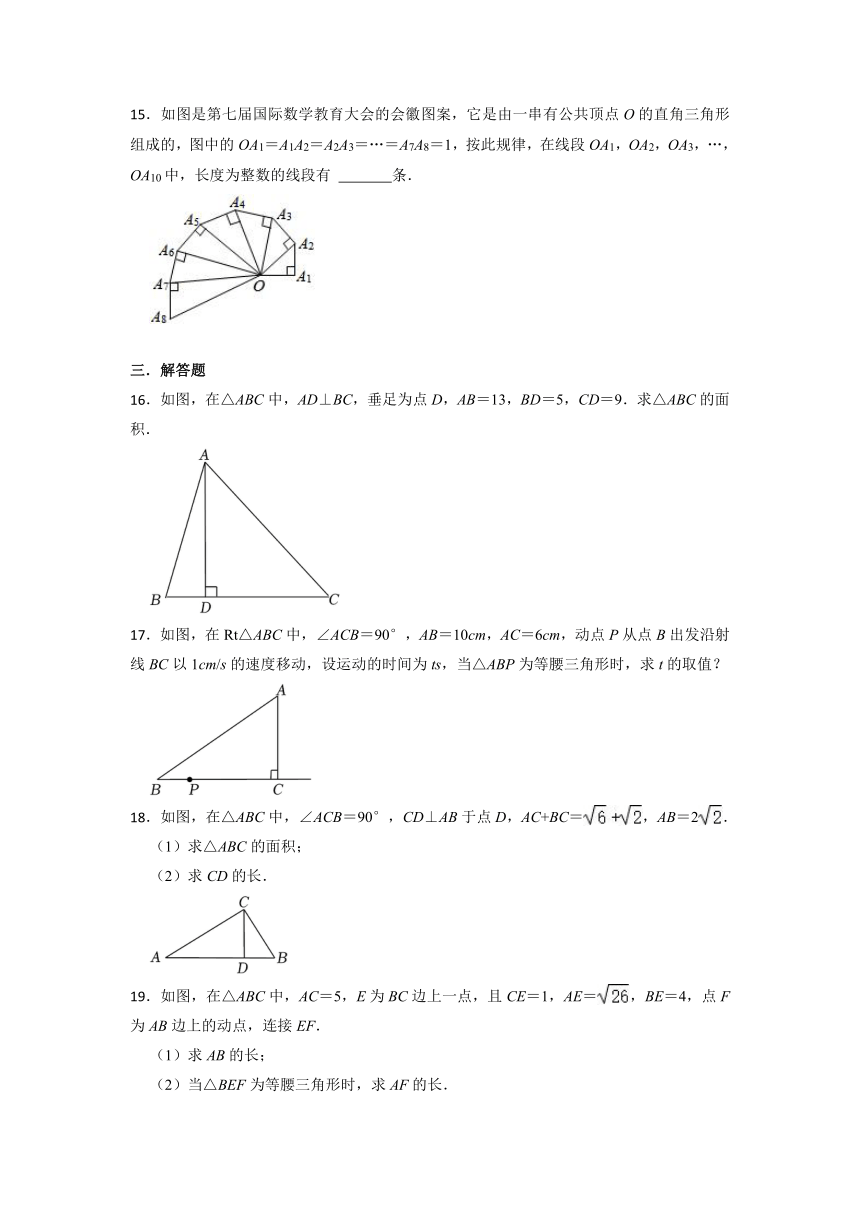
.如图是第七届国际数学教育大会的会徽图案,它是由一串有公共顶点O的直角三角形组成的,图中的OA1=A1A2=A2A3=…=A7A8=1,按此规律,在线段OA1,OA2,OA3,…,OA10中,长度为整数的线段有 条.
三.解答题
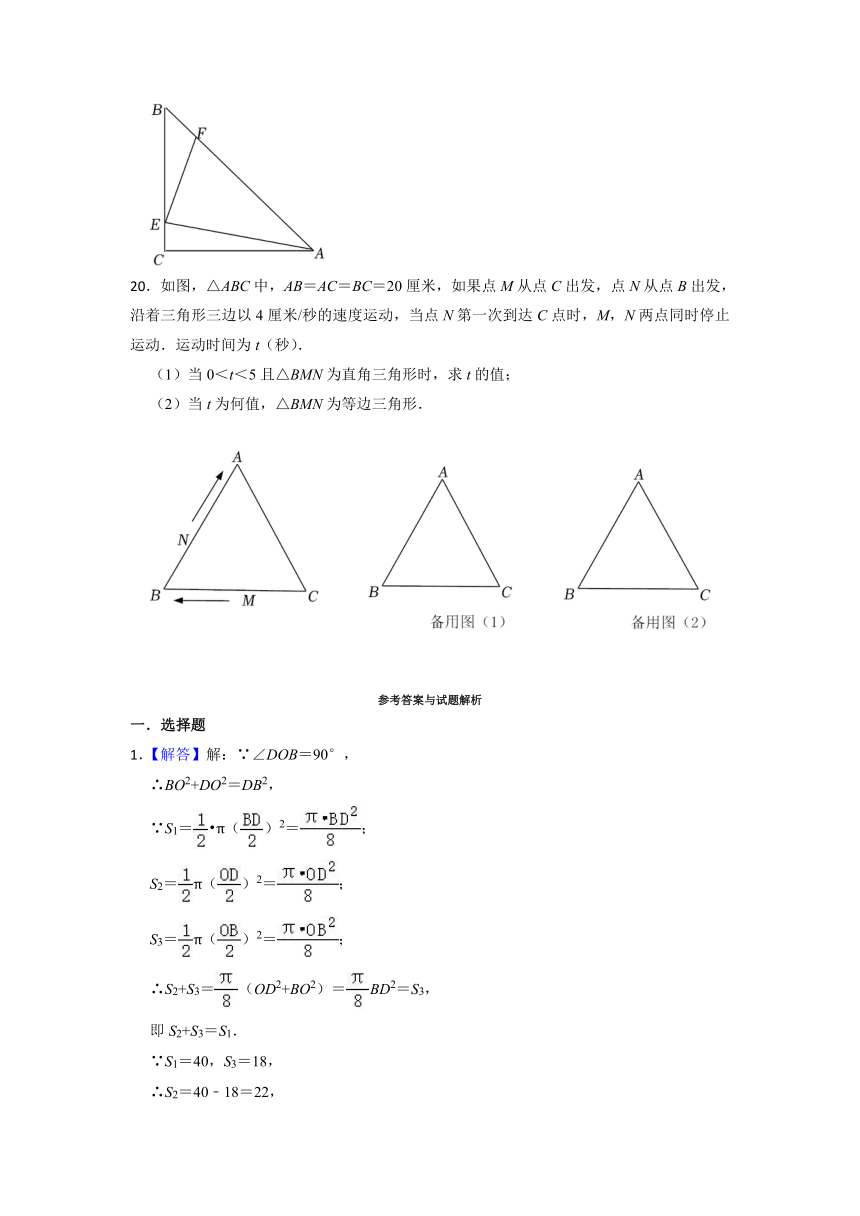
.如图,在△ABC中,AD⊥BC,垂足为点D,AB=13,BD=5,CD=9.求△ABC的面积.
.如图,在Rt△ABC中,∠ACB=90°,AB=10cm,AC=6cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为ts,当△ABP为等腰三角形时,求t的取值?
.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,AC+BC=,AB=2.
(1)求△ABC的面积;
(2)求CD的长.
.如图,在△ABC中,AC=5,E为BC边上一点,且CE=1,AE=,BE=4,点F为AB边上的动点,连接EF.
(1)求AB的长;
(2)当△BEF为等腰三角形时,求AF的长.
.如图,△ABC中,AB=AC=BC=20厘米,如果点M从点C出发,点N从点B出发,沿着三角形三边以4厘米/秒的速度运动,当点N第一次到达C点时,M,N两点同时停止运动.运动时间为t(秒).
(1)当0<t<5且△BMN为直角三角形时,求t的值;
(2)当t为何值,△BMN为等边三角形.
参考答案与试题解析
一.选择题
.【解答】解:∵∠DOB=90°,
∴BO2+DO2=DB2,
∵S1= π()2=;
S2=π()2=;
S3=π()2=;
∴S2+S3=(OD2+BO2)=BD2=S3,
即S2+S3=S1.
∵S1=40,S3=18,
∴S2=40﹣18=22,
故选:C.
.【解答】解:依题意“弦”为=,
而3.5=<<=4,
∴“弦”最接近的整数是4.
故选:D.
.【解答】解:连接AC,BC,设点C到线段AB所在直线的距离是h,
∵S△ABC=2×2﹣1×2﹣﹣=,
AB==,
∴×h=,
∴h=,
故点C到AB的距离是,
故选:D.
.【解答】解:如图所示:△MNP为等腰直角三角形,∠MPN=45°,此时PM最长,
根据勾股定理得:PM===2.
故选:C.
.【解答】解:设Rt△ABC的第三边长为x,
①当12为直角三角形的直角边时,x为斜边,
由勾股定理得,x==13,此时这个三角形的周长=5+12+13=30;
②当12为直角三角形的斜边时,x为直角边,
由勾股定理得,x==,此时这个三角形的周长=5+12+=+17,
综上所述,该三角形的周长为30或+17.
故选:C.
.【解答】解:当m为斜边时:32+42=m2,
解得:m1=5,m2=﹣5(不符合题意);
当m为直角边时:32+m2=42,
解得:m1=,m2=﹣(不符合题意).
故第三边长m为5或,
∴实数m的相反数为﹣5或﹣.
故选:D.
.【解答】解:∵正方形EFGH的面积=正方形ABCD的面积﹣4S△ABE=92﹣4×18=9,
∴正方形EFGH的边长=3,
故小正方形的边长为3,
故选:C.
.【解答】解:连接AD,
∵DE是线段AB的垂直平分线,
∴DB=DA,
设DB=x,则CD=BC﹣DB=18﹣x,
∵∠C=90°,AC=12,
∴AD2=CD2+AC2,
∴x2=(18﹣x)2+122,
解得x=13,
即BD=13,
故选:C.
.【解答】解:过点B作BH⊥AC于点H,过点D作DG⊥AC于点G,如图所示:
则∠BHC=90°,∠AGD=90°,
∵∠B=∠D=90°,∠BAC=30°,
∴∠BCA=60°,
∴∠CBH=30°,
∵BC=4,
∴HC=2,
根据勾股定理,得HB=2,
∴点P在点B处时,点P到AC的距离为2,
∵∠CAD=45°,
∴∠ACD=45°,
∴△ADC是等腰直角三角形,
∴GD=AC
∵AC=2BC=8,
∴GD=4,
∵4>2,
∴在AD边和CD边上各有一点P,使得点P到AC的距离为2,
综上,满足条件的点P有3处,
故选:C.
.【解答】解:由图可得,
a2+b2=c2=25,故①正确;
∵小正方形面积为1,
∴小正方形的边长为1,
∴a﹣b=1,故②正确;
∵大正方形面积为25,小正方形面积为1,
∴ab=(25﹣1)÷4,
解得ab=12,故③正确;
∵a2+b2=25,ab=12,
∴(a+b)2=a2+2ab+b2=49,
∴a+b=7,故④正确;
故选:D.
二.填空题
.【解答】解:分两种情况:
①当3和4都为直角边时,
由勾股定理得斜边长为:=5;
②当4为斜边时,斜边=4;
综上所述:该直角三角形的斜边长为5或4.
故答案为:5或4.
.【解答】解:∵BC的垂直平分线交AC于点D,
∴BD=CD,
在Rt△ABC中,由勾股定理得,AC=4,
设AD=x,则CD=BD=4﹣x,
在Rt△ABD中,由勾股定理得,
x2+32=(4﹣x)2,
解得x=,
∴AD=,
故答案为:.
.【解答】解:∵AB=8,BC=10,∠BAC=90°,
∴AC===6,
分别以△ABC的三条边为直径向外作半圆,其半圆的面积由小到大分别记作S1、S2、S3,
由圆的面积计算公式知:S3=πBC2,S2=πAC2,S1=πAB2,
则S1+S2=π(AB2+AC2),
在Rt△ABC中,∠BAC=90°,
∴AB2+AC2=CB2,
∴S1+S2=S3.
∵阴影部分面积等于:S1+S2+S△ABC﹣S3=S△ABC=×6×8=24,
故答案为:24.
.【解答】解:∵AC=BC,∠C=90°,
∴AC=AB=2,
∵AD是△ABC的角平分线,
∴∠DAC=∠DAE,
∵∠C=∠AED=90°,
∴∠ADC=∠ADE,
∴AC=AE,
∴BE=AB﹣AE=4﹣2,
∵∠B=45°,∠DEB=90°,
∴∠EDB=∠B=45°,
∴DE=BE,
∵AD是△ABC的角平分线,DE⊥AB,∠C=90°,
∴CD=DE=4﹣2,
故答案为:4﹣2.
.【解答】解:∵OA1=1,
∴由勾股定理可得OA2==,
OA3=,
…,
∴OAn=,
∴在线段OA1,OA2,OA3,…,OA10中,完全平方数有1,4,9,
故长度为整数的线段有3条.
故答案为:3.
三.解答题
.【解答】解:∵AD⊥BC,
∴∠ADB=90°,
∵AB=13,BD=5,
∴AD===12,
∵CD=9,
∴BC=BD+CD=14,
∴△ABC的面积=BC AD
=×14×12
=84,
∴△ABC的面积为84.
.【解答】解:在Rt△ABC中,∠ACB=90°,
由勾股定理得:BC==8(cm),
当AB=AP时,由△ABC≌△APC可知:
PC=BC=8cm,
∴BP=16cm,
∴t=16,
当BA=BP时,BP=10cm,
∴t=10,
当PA=PB时,设BP=xcm,
在Rt△ACP中,
由勾股定理得:
(8﹣x)2+62=x2,
∴x=,
∴BP=cm,
∴t=,
故t的取值为:16或10或.
.【解答】解:(1)在△ABC中,∠ACB=90°,
∴AC2+BC2=AB2,
∵AC+BC=,
∴(AC+BC)2=AC2+BC2+2AC BC=8+4,
∵AB=2,
∴AB2=8,
∴AC BC=2,
∴△ABC的面积=AC BC=;
(2)∵△ABC的面积=AC BC=,CD⊥AB,
∴AB CD=,
∴CD==.
.【解答】解:(1)∵AC=5,CE=1,AE=,
∴AC2+CE2=26,AE2=26,
∴AC2+CE2=AE2,
∴∠ACE=90°,
∵BC=CE+BE=5,AC=5,
∴AB===5;
(2)①当BF=BE=4时,
AF=AB﹣BF=5﹣4;
②如图,当BF=EF时,有∠FEB=∠B=45°,
∴∠BFE=90°,BF=EF,
设BF=EF=x,
∵BF2+EF2=BE2,
∴x2+x2=42,
∴x=2(负值舍去),
∴AF=AB﹣BF=5﹣2=3;
③如图,当BE=EF时,有∠EFB=∠B=45°,
∴∠BEF=90°,EF=BE=4,
∴BF==4,
∴AF=AB﹣BF=5.
综上所述,AF的长为5﹣4或3或.
.【解答】解:(1)当0<t<5时,点M在BC上,点N在AB上,BN=4t,MB=20﹣4t,
△BMN为直角三角形,则∠BNM=90°或∠NMB=90°,
①当∠BNM=90°时,
∵∠B=60°,
∴∠BMN=90°﹣∠B=90°﹣60°=30°,
∴BM=2BN,
∴20﹣4t=2×4t,
解得:t=;
②当∠NMB=90°时,
∵∠B=60°,
∴∠BNM=90°﹣∠B=90°﹣60°=30°,
∴BN=2BM,
∴4t=2(20﹣4t),
解得:t=.
③点M在AC上,点N在AB上,AN=CM=40﹣4t,(80﹣8t)+(40﹣4t)=20,
t=(不合题意舍去),
综上,当t=或时,△BMN为直角三角形;
(2)点N第一次到达C点时,M,N两点同时停止运动,则0<t≤10,
①当0<t≤5时,当MB=BN时,△BMN为等边三角形,
此时,4t=20﹣4t,
解得:t=;
②当5<t≤10时,△BMN为等边三角形,只能点M与点A重合,点N与点C重合,
此时,t=10,
综上,t=或t=10时,△BMN为等边三角形.
一.选择题
.如图,在Rt△BOD中,分别以BD,OD,BO为直径向外作三个半圆,其面积分别为S1,S2,S3,若S1=40,S3=18,则S2=( )
A.18 B.20 C.22 D.24
.勾股定理在《九章算术》中的表述是:“勾股术曰:勾股各自乘,并而开方除之,即弦”.即c=(a为勾,b为股,c为弦),若“勾”为2,“股”为3,则“弦”最接近的整数是( )
A.1 B.2 C.3 D.4
.点A、B、C在格点图中的位置如图所示,格点小正方形的边长为1,则点C到AB的距离是( )
A. B. C. D.
.在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.如图,在6×6的正方形网格图形ABCD中,M,N分别是AB,BC上的格点,BM=4,BN=2.若点P是这个网格图形中的格点,连结PM,PN,则所有满足∠MPN=45°的△PMN中,边PM的长的最大值是( )
A.4 B.6 C.2 D.3
.已知直角三角形两边的长为5和12,则此三角形的周长为( )
A.30 B.+17 C.+17或30 D.36
.已知3,4,m是一个直角三角形的三条边长,则实数m的相反数为( )
A.5 B.﹣5 C.5或 D.﹣5或﹣
.如图,这是用面积为18的四个全等的直角三角形拼成的“赵爽弦图”.如果大正方形的边长为9,那么小正方形的边长为( )
A.1 B.2 C.3 D.4
.如图,在Rt△ABC中,∠C=90°,AC=12,BC=18,DE是线段AB的垂直平分线,则BD的长为( )
A.8 B.10 C.13 D.15
.如图所示,在四边形ABCD中,∠B=∠D=90°,∠BAC=30°,∠CAD=45°,BC=4,点P是四边形ABCD边上的一个动点,若点P到AC的距离为2,则点P的位置有( )
A.1处 B.2处 C.3处 D.4处
.勾股定理被誉为“几何明珠”,如图是我国古代著名的“赵爽弦图”,它由4个全等的直角三角形拼成,已知大正方形面积为25,小正方形面积为1,若用a、b表示直角三角形的两直角边(a>b),则下列说法:①a2+b2=25,②a﹣b=1,③ab=12,④a+b=7.正确的是( )
A.①② B.①②③ C.①②④ D.①②③④
二.填空题
.若直角三角形的两边长分别为3,4,则该直角三角形的斜边长为 .
.如图,在Rt△ABC中,∠A=90°,AB=3,BC=5,BC的垂直平分线交AC于点D,垂足为点E,则AD= .
.已知Rt△ABC中,AB=8,BC=10,∠BAC=90°,则图中阴影部分面积为 .
.如图,在△ABC中,AC=BC,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为E,若AB=4,则CD= .
.如图是第七届国际数学教育大会的会徽图案,它是由一串有公共顶点O的直角三角形组成的,图中的OA1=A1A2=A2A3=…=A7A8=1,按此规律,在线段OA1,OA2,OA3,…,OA10中,长度为整数的线段有 条.
三.解答题
.如图,在△ABC中,AD⊥BC,垂足为点D,AB=13,BD=5,CD=9.求△ABC的面积.
.如图,在Rt△ABC中,∠ACB=90°,AB=10cm,AC=6cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为ts,当△ABP为等腰三角形时,求t的取值?
.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,AC+BC=,AB=2.
(1)求△ABC的面积;
(2)求CD的长.
.如图,在△ABC中,AC=5,E为BC边上一点,且CE=1,AE=,BE=4,点F为AB边上的动点,连接EF.
(1)求AB的长;
(2)当△BEF为等腰三角形时,求AF的长.
.如图,△ABC中,AB=AC=BC=20厘米,如果点M从点C出发,点N从点B出发,沿着三角形三边以4厘米/秒的速度运动,当点N第一次到达C点时,M,N两点同时停止运动.运动时间为t(秒).
(1)当0<t<5且△BMN为直角三角形时,求t的值;
(2)当t为何值,△BMN为等边三角形.
参考答案与试题解析
一.选择题
.【解答】解:∵∠DOB=90°,
∴BO2+DO2=DB2,
∵S1= π()2=;
S2=π()2=;
S3=π()2=;
∴S2+S3=(OD2+BO2)=BD2=S3,
即S2+S3=S1.
∵S1=40,S3=18,
∴S2=40﹣18=22,
故选:C.
.【解答】解:依题意“弦”为=,
而3.5=<<=4,
∴“弦”最接近的整数是4.
故选:D.
.【解答】解:连接AC,BC,设点C到线段AB所在直线的距离是h,
∵S△ABC=2×2﹣1×2﹣﹣=,
AB==,
∴×h=,
∴h=,
故点C到AB的距离是,
故选:D.
.【解答】解:如图所示:△MNP为等腰直角三角形,∠MPN=45°,此时PM最长,
根据勾股定理得:PM===2.
故选:C.
.【解答】解:设Rt△ABC的第三边长为x,
①当12为直角三角形的直角边时,x为斜边,
由勾股定理得,x==13,此时这个三角形的周长=5+12+13=30;
②当12为直角三角形的斜边时,x为直角边,
由勾股定理得,x==,此时这个三角形的周长=5+12+=+17,
综上所述,该三角形的周长为30或+17.
故选:C.
.【解答】解:当m为斜边时:32+42=m2,
解得:m1=5,m2=﹣5(不符合题意);
当m为直角边时:32+m2=42,
解得:m1=,m2=﹣(不符合题意).
故第三边长m为5或,
∴实数m的相反数为﹣5或﹣.
故选:D.
.【解答】解:∵正方形EFGH的面积=正方形ABCD的面积﹣4S△ABE=92﹣4×18=9,
∴正方形EFGH的边长=3,
故小正方形的边长为3,
故选:C.
.【解答】解:连接AD,
∵DE是线段AB的垂直平分线,
∴DB=DA,
设DB=x,则CD=BC﹣DB=18﹣x,
∵∠C=90°,AC=12,
∴AD2=CD2+AC2,
∴x2=(18﹣x)2+122,
解得x=13,
即BD=13,
故选:C.
.【解答】解:过点B作BH⊥AC于点H,过点D作DG⊥AC于点G,如图所示:
则∠BHC=90°,∠AGD=90°,
∵∠B=∠D=90°,∠BAC=30°,
∴∠BCA=60°,
∴∠CBH=30°,
∵BC=4,
∴HC=2,
根据勾股定理,得HB=2,
∴点P在点B处时,点P到AC的距离为2,
∵∠CAD=45°,
∴∠ACD=45°,
∴△ADC是等腰直角三角形,
∴GD=AC
∵AC=2BC=8,
∴GD=4,
∵4>2,
∴在AD边和CD边上各有一点P,使得点P到AC的距离为2,
综上,满足条件的点P有3处,
故选:C.
.【解答】解:由图可得,
a2+b2=c2=25,故①正确;
∵小正方形面积为1,
∴小正方形的边长为1,
∴a﹣b=1,故②正确;
∵大正方形面积为25,小正方形面积为1,
∴ab=(25﹣1)÷4,
解得ab=12,故③正确;
∵a2+b2=25,ab=12,
∴(a+b)2=a2+2ab+b2=49,
∴a+b=7,故④正确;
故选:D.
二.填空题
.【解答】解:分两种情况:
①当3和4都为直角边时,
由勾股定理得斜边长为:=5;
②当4为斜边时,斜边=4;
综上所述:该直角三角形的斜边长为5或4.
故答案为:5或4.
.【解答】解:∵BC的垂直平分线交AC于点D,
∴BD=CD,
在Rt△ABC中,由勾股定理得,AC=4,
设AD=x,则CD=BD=4﹣x,
在Rt△ABD中,由勾股定理得,
x2+32=(4﹣x)2,
解得x=,
∴AD=,
故答案为:.
.【解答】解:∵AB=8,BC=10,∠BAC=90°,
∴AC===6,
分别以△ABC的三条边为直径向外作半圆,其半圆的面积由小到大分别记作S1、S2、S3,
由圆的面积计算公式知:S3=πBC2,S2=πAC2,S1=πAB2,
则S1+S2=π(AB2+AC2),
在Rt△ABC中,∠BAC=90°,
∴AB2+AC2=CB2,
∴S1+S2=S3.
∵阴影部分面积等于:S1+S2+S△ABC﹣S3=S△ABC=×6×8=24,
故答案为:24.
.【解答】解:∵AC=BC,∠C=90°,
∴AC=AB=2,
∵AD是△ABC的角平分线,
∴∠DAC=∠DAE,
∵∠C=∠AED=90°,
∴∠ADC=∠ADE,
∴AC=AE,
∴BE=AB﹣AE=4﹣2,
∵∠B=45°,∠DEB=90°,
∴∠EDB=∠B=45°,
∴DE=BE,
∵AD是△ABC的角平分线,DE⊥AB,∠C=90°,
∴CD=DE=4﹣2,
故答案为:4﹣2.
.【解答】解:∵OA1=1,
∴由勾股定理可得OA2==,
OA3=,
…,
∴OAn=,
∴在线段OA1,OA2,OA3,…,OA10中,完全平方数有1,4,9,
故长度为整数的线段有3条.
故答案为:3.
三.解答题
.【解答】解:∵AD⊥BC,
∴∠ADB=90°,
∵AB=13,BD=5,
∴AD===12,
∵CD=9,
∴BC=BD+CD=14,
∴△ABC的面积=BC AD
=×14×12
=84,
∴△ABC的面积为84.
.【解答】解:在Rt△ABC中,∠ACB=90°,
由勾股定理得:BC==8(cm),
当AB=AP时,由△ABC≌△APC可知:
PC=BC=8cm,
∴BP=16cm,
∴t=16,
当BA=BP时,BP=10cm,
∴t=10,
当PA=PB时,设BP=xcm,
在Rt△ACP中,
由勾股定理得:
(8﹣x)2+62=x2,
∴x=,
∴BP=cm,
∴t=,
故t的取值为:16或10或.
.【解答】解:(1)在△ABC中,∠ACB=90°,
∴AC2+BC2=AB2,
∵AC+BC=,
∴(AC+BC)2=AC2+BC2+2AC BC=8+4,
∵AB=2,
∴AB2=8,
∴AC BC=2,
∴△ABC的面积=AC BC=;
(2)∵△ABC的面积=AC BC=,CD⊥AB,
∴AB CD=,
∴CD==.
.【解答】解:(1)∵AC=5,CE=1,AE=,
∴AC2+CE2=26,AE2=26,
∴AC2+CE2=AE2,
∴∠ACE=90°,
∵BC=CE+BE=5,AC=5,
∴AB===5;
(2)①当BF=BE=4时,
AF=AB﹣BF=5﹣4;
②如图,当BF=EF时,有∠FEB=∠B=45°,
∴∠BFE=90°,BF=EF,
设BF=EF=x,
∵BF2+EF2=BE2,
∴x2+x2=42,
∴x=2(负值舍去),
∴AF=AB﹣BF=5﹣2=3;
③如图,当BE=EF时,有∠EFB=∠B=45°,
∴∠BEF=90°,EF=BE=4,
∴BF==4,
∴AF=AB﹣BF=5.
综上所述,AF的长为5﹣4或3或.
.【解答】解:(1)当0<t<5时,点M在BC上,点N在AB上,BN=4t,MB=20﹣4t,
△BMN为直角三角形,则∠BNM=90°或∠NMB=90°,
①当∠BNM=90°时,
∵∠B=60°,
∴∠BMN=90°﹣∠B=90°﹣60°=30°,
∴BM=2BN,
∴20﹣4t=2×4t,
解得:t=;
②当∠NMB=90°时,
∵∠B=60°,
∴∠BNM=90°﹣∠B=90°﹣60°=30°,
∴BN=2BM,
∴4t=2(20﹣4t),
解得:t=.
③点M在AC上,点N在AB上,AN=CM=40﹣4t,(80﹣8t)+(40﹣4t)=20,
t=(不合题意舍去),
综上,当t=或时,△BMN为直角三角形;
(2)点N第一次到达C点时,M,N两点同时停止运动,则0<t≤10,
①当0<t≤5时,当MB=BN时,△BMN为等边三角形,
此时,4t=20﹣4t,
解得:t=;
②当5<t≤10时,△BMN为等边三角形,只能点M与点A重合,点N与点C重合,
此时,t=10,
综上,t=或t=10时,△BMN为等边三角形.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
