2023年韩国高考(大学修学能力考试)数学试卷(图片版,无答案)
文档属性
| 名称 | 2023年韩国高考(大学修学能力考试)数学试卷(图片版,无答案) |  | |
| 格式 | |||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-27 13:46:07 | ||
图片预览


文档简介
2023学年度韩国高考(大学修学能力考试)
数学
考试时间:10M分钟
试卷满分:100分
第〡卷必答部分
单项选择题
2◆
4
25
的值为2分]
@
③1
④2
⑤4
2.1im
2-2+3江的值为2分]
r+5
①I
②2
③3
④4
⑤5
3.在公比为正数的容比数列,中,+,=30,+=兰则a,的值为B州
①48
②56
③64
④72
⑤80
4.(x)为多项式函数g(x)=x2∫x1.若2)=1(2)=3,则g2)的值为3分]
①12
②14
③16
④18
⑤20
5.己知an0<0.cs
侵+0小-,则e0的值为B分
0-2⑤
②-E
③0
⑤25
5
5
5
6.己知函数(x)=2r3-9x2+x+5在x=1处取得极大值,在x=b处取得极小值,则a+b的值
为[3分]
①12
②14
③16
④18
⑤20
7.等差数列。的各项均为正数.首项与公差相等,】
=2,则a,的值为[3分]
回,+1+1
①6
②7
③8
④9
⑤I0
8.过点(0.4)作曲线y=x3-x+2的切线,这条切线在x轴上的截距为3分]
0吃
②-1
④-2
9.函数)=a-万1m2在闭区间-石6]上的最大值为,最小值为3,则a×6的值为4分]
0罗
③
=r-
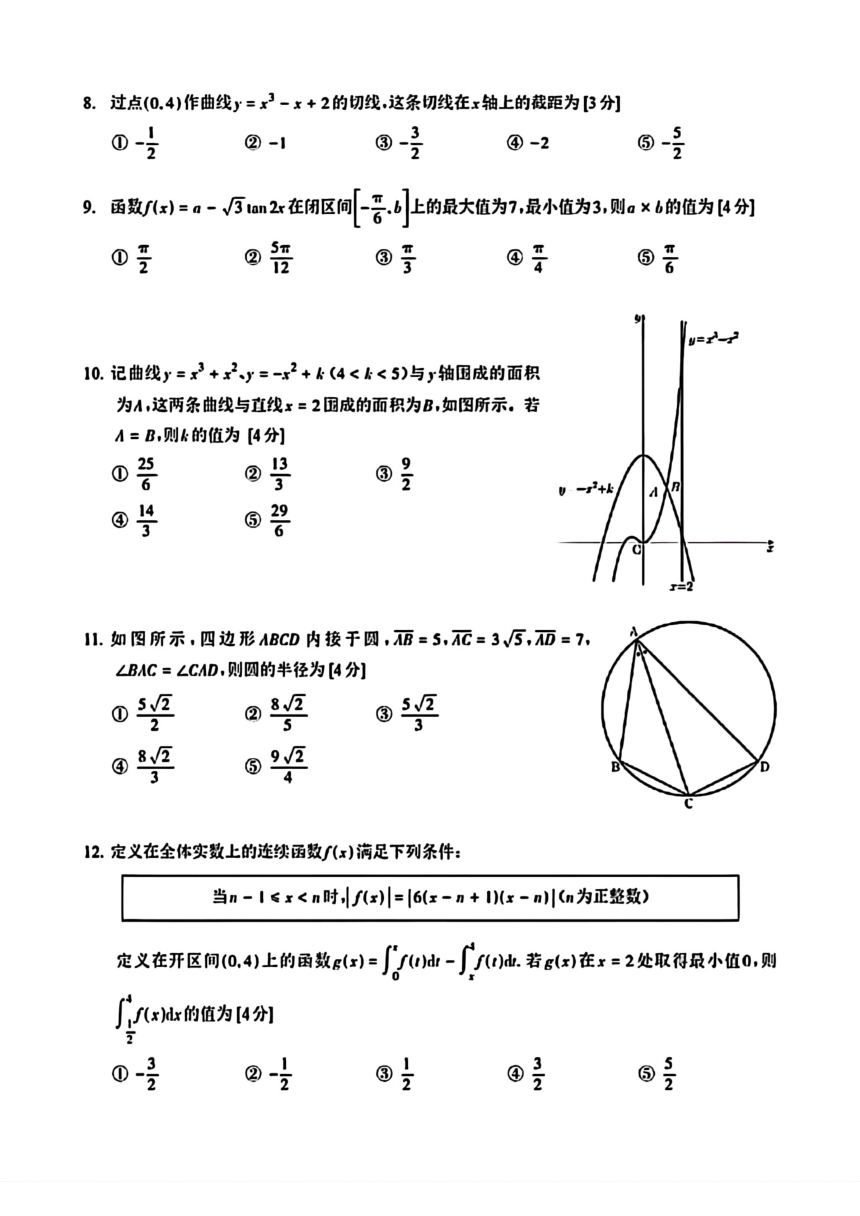
10.记曲线y=x3+x2y=-2+k(4为A,这两条曲线与直线x=2国成的面积为B,如图所示。若
A=B,则k的值为[4分]
①客
②号
0--2+k
⑧号
⑤
11.如图所示,四边形ABCD内接于圆,丽=5,AC=3√5,而=7,
∠BAC=∠CAD,则圆的半径为[4分]
052
②82
③52
2
5
3
④8?
3
⑤92
4
12.定义在全体实数上的述铁函数(x)满足下列条件:
当n-I≤x定义在开区间0,4)上的虽数g-0地-∫0)恤.若6在x=2处取符录小值0,则
∫出的值为4分剂
@
⑤
13.对于正整数m(m≥2),使得m12的n次方根为整数的正整数n(n≥2)的个数记为f(m),则
m)的值为A分别1
m=2
①37
②42
③47
④52
⑤57
14.(x)为多项式函数,g(x)定义如下
(x<-1或r>I)
f(x)(1≤x≤I)
关于函数h(x)=lim,g(x+)×1im,g(x+小.下列说法正确的是【4分]
。=0
1-29
甲.h(1)=3
乙.h(x)在全体实数上连续
丙.若g(x)在区问-1,1小上单调递减,且g(-1)=-2,则(x)在全体实数上具有最小值。
①甲
②乙
③甲、乙
④甲、丙
⑤乙、丙
15.在各项均为正整数,且满足下列条件的数列a。中,0,可能的最大值和最小值分别为训和m,则
M+m的值为[4分]
(1)a2=40
(2)对于任意正整数n,
nn+1+n(an+1不是3的倍数)
0n◆2=
3+1
(an+1是3的倍数)
①216
②218
③220
④222
⑤224
短答题
16.求满足方程1og2(3x+2)=2+1g2(x-2)的x值。[3分]
17.对于函数f(x),已知f"(x)=4x23-2r,且f(0)=3,求∫(2)的值。[3分]
Ia数k简是含a:+51=5,含a:+6=2R宫A的值.B州
19.求使方程2x-6x2+k=0怡有2个互异实数解的整数k共有多少个。[3分]
数学
考试时间:10M分钟
试卷满分:100分
第〡卷必答部分
单项选择题
2◆
4
25
的值为2分]
@
③1
④2
⑤4
2.1im
2-2+3江的值为2分]
r+5
①I
②2
③3
④4
⑤5
3.在公比为正数的容比数列,中,+,=30,+=兰则a,的值为B州
①48
②56
③64
④72
⑤80
4.(x)为多项式函数g(x)=x2∫x1.若2)=1(2)=3,则g2)的值为3分]
①12
②14
③16
④18
⑤20
5.己知an0<0.cs
侵+0小-,则e0的值为B分
0-2⑤
②-E
③0
⑤25
5
5
5
6.己知函数(x)=2r3-9x2+x+5在x=1处取得极大值,在x=b处取得极小值,则a+b的值
为[3分]
①12
②14
③16
④18
⑤20
7.等差数列。的各项均为正数.首项与公差相等,】
=2,则a,的值为[3分]
回,+1+1
①6
②7
③8
④9
⑤I0
8.过点(0.4)作曲线y=x3-x+2的切线,这条切线在x轴上的截距为3分]
0吃
②-1
④-2
9.函数)=a-万1m2在闭区间-石6]上的最大值为,最小值为3,则a×6的值为4分]
0罗
③
=r-
10.记曲线y=x3+x2y=-2+k(4
A=B,则k的值为[4分]
①客
②号
0--2+k
⑧号
⑤
11.如图所示,四边形ABCD内接于圆,丽=5,AC=3√5,而=7,
∠BAC=∠CAD,则圆的半径为[4分]
052
②82
③52
2
5
3
④8?
3
⑤92
4
12.定义在全体实数上的述铁函数(x)满足下列条件:
当n-I≤x
∫出的值为4分剂
@
⑤
13.对于正整数m(m≥2),使得m12的n次方根为整数的正整数n(n≥2)的个数记为f(m),则
m)的值为A分别1
m=2
①37
②42
③47
④52
⑤57
14.(x)为多项式函数,g(x)定义如下
(x<-1或r>I)
f(x)(1≤x≤I)
关于函数h(x)=lim,g(x+)×1im,g(x+小.下列说法正确的是【4分]
。=0
1-29
甲.h(1)=3
乙.h(x)在全体实数上连续
丙.若g(x)在区问-1,1小上单调递减,且g(-1)=-2,则(x)在全体实数上具有最小值。
①甲
②乙
③甲、乙
④甲、丙
⑤乙、丙
15.在各项均为正整数,且满足下列条件的数列a。中,0,可能的最大值和最小值分别为训和m,则
M+m的值为[4分]
(1)a2=40
(2)对于任意正整数n,
nn+1+n(an+1不是3的倍数)
0n◆2=
3+1
(an+1是3的倍数)
①216
②218
③220
④222
⑤224
短答题
16.求满足方程1og2(3x+2)=2+1g2(x-2)的x值。[3分]
17.对于函数f(x),已知f"(x)=4x23-2r,且f(0)=3,求∫(2)的值。[3分]
Ia数k简是含a:+51=5,含a:+6=2R宫A的值.B州
19.求使方程2x-6x2+k=0怡有2个互异实数解的整数k共有多少个。[3分]
同课章节目录
