2023-2024学年天津市自立中学高一上学期数学必修第一册期末综合模拟测试卷(含解析)
文档属性
| 名称 | 2023-2024学年天津市自立中学高一上学期数学必修第一册期末综合模拟测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 945.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-09-08 15:09:30 | ||
图片预览




文档简介
北师大版数学必修第一册期末综合模拟测试卷
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知不等式的解集为,则不等式的解集为( )
A. B.C. D.
2.若函数的定义域是,则函数的定义域为( )
A. B. C. D.
3.已知函数,若函数在开区间上恒有最小值,则实数的取值范围为( ).
A. B.
C. D.
4.已知,,,则( )
A. B. C. D.
5.设,函数在上单调递减,则( )
A.在上单调递减,在上单调递增
B.在上单调递增,在上单调递减
C.在上单调递增,在上单调递增
D.在上单调递减,在上单调递减
6.已知函数,若关于的方程有4个不同的实数根,且所有实数根之和为2,则实数的取值范围是( )
A. B. C. D.
7.为了提高幼儿园孩子认识数字的能力,老师任意选取两个小朋友,让他们每人从1,2,3,4,5,6这六个数字当中任选一个数字(两人所选的数字可以相同),如果所选出的两个数字相差不超过1,则称这两个小朋友“心有灵犀”.两个小朋友“心有灵犀”的概率为( )
A. B. C. D.
8.已知函数.下列命题正确的是( )
A.必是偶函数
B.当时,的图像关于直线对称
C.若,则在区间上是增函数
D.有最大值
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对得5分,选对但不全的得3分,有选错的得0分)
9.对任意实数.若不等式恒成立,则实数可取的值为( )
A. B. C. D.
10.给出以下四个结论,其中所有正确结论的序号是( )
A.若函数的定义域为,则函数的定义域是;
B.函数(其中,且)的图象过定点;
C.当时,幂函数的图象是一条直线;
D.若,则的取值范围是.
11.已知函数,若函数恰有个零点,则实数可以是( )
A. B. C. D.
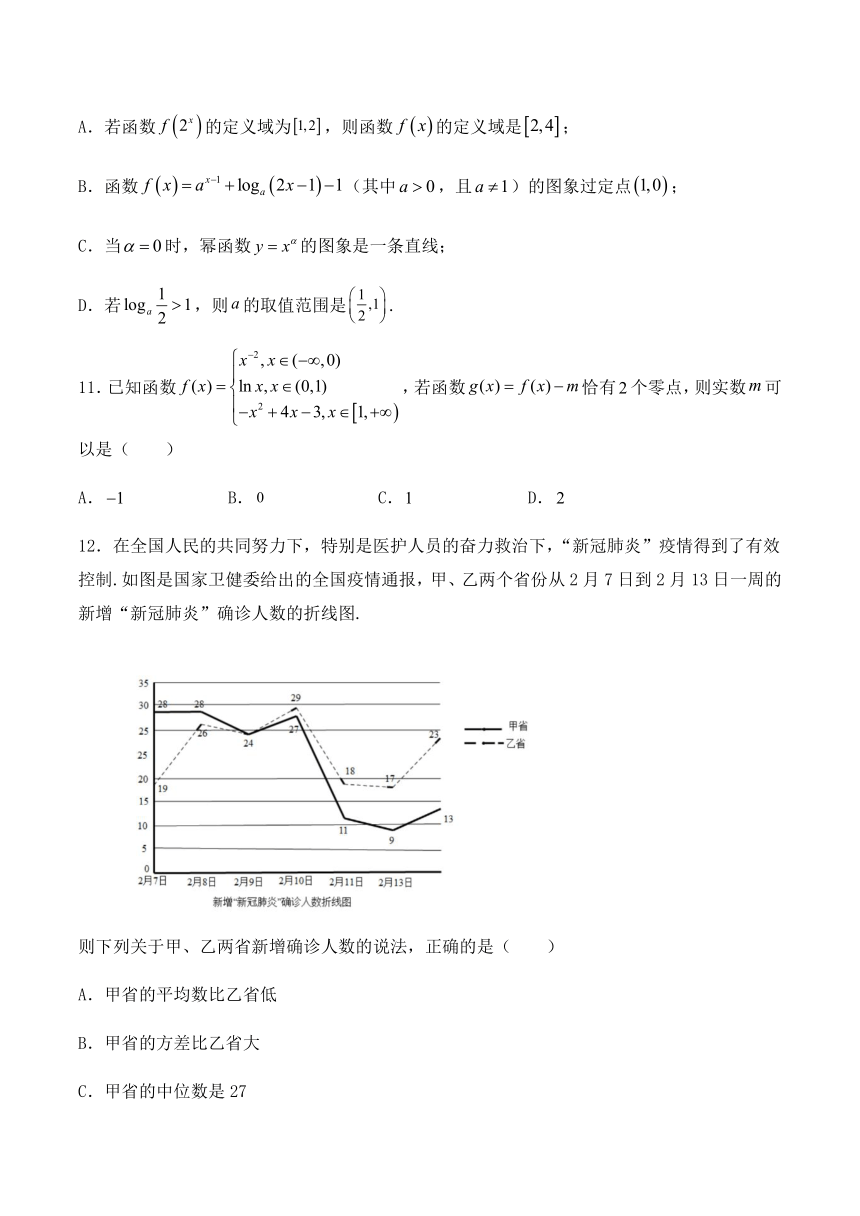
12.在全国人民的共同努力下,特别是医护人员的奋力救治下,“新冠肺炎”疫情得到了有效控制.如图是国家卫健委给出的全国疫情通报,甲、乙两个省份从2月7日到2月13日一周的新增“新冠肺炎”确诊人数的折线图.
则下列关于甲、乙两省新增确诊人数的说法,正确的是( )
A.甲省的平均数比乙省低
B.甲省的方差比乙省大
C.甲省的中位数是27
D.乙省的极差是12
三、填空题(本大题共4小题,每小题5分,共20分,请把正确答案填在题中横线上)
13.计算:_________.
14.设函数为定义在上的奇函数,且当时,(其中为实数),则的值为________.
15.《易经》是中国传统文化中的精髓,下图是易经八卦图(含乾、坤、巽、震、坎、离、艮、兑八卦),每一卦由三根线组成(表示一根阳线,表示一根阴线),从八卦中任取一卦,这一卦的三根线中恰有2根阳线和1根阴线的概率_____.
16.已知函数,若函数有6个不同的零点,则实数m的范围是_______.
四、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明,证明过程或演算步骤)
17.(本小题满分10分)已知二次函数.
(1)若的解集为,解关于x的不等式;
(2)若不等式对恒成立,求的最大值.
19.(本小题满分12分)已知函数为奇函数.
(1)求实数a的值并证明是增函数;
(2)若实数满足不等式,求t的取值范围.
20.(本小题满分12分)已知且,.
(1)求函数的解析式,并判断其奇偶性和单调性;
(2)当的定义域为时,解关于的不等式
(3)若恰在上取负值,求的值.
21.(本小题满分12分)某厂家拟定在2020年举行促销活动,经调查测算,该产品的年销量(即该厂的年产量)x万件与年促销费用m(m≥0)万元满足x=3- (k为常数).如果不搞促销活动,那么该产品的年销量只能是1万件.已知2020年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2020年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2020年的促销费用投入多少万元时,厂家利润最大?
22.(本小题满分12分)某城市交通部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照分成5组,制成如图所示频率分直方图.
(1)求图中的值;
(2)求这组数据的平均数和中位数;
(3)已知满意度评分值在内的男生数与女生数的比为3:2,若在满意度评分值为的人中随机抽取2人进行座谈,求2人均为男生的概率.
23.(本小题满分12分)已知函数
(1)若,求证:函数恰有一个正零点;(用图像法证明不给分)
(2)若函数恰有三个零点,求实数取值范围.
试卷第1页,总3页
参考答案
1.C
不等式的解集为,
和2是方程的两个根,且,
, 可得,
则不等式等价于,
即,解得或,
故不等式的解集为.
2.C
函数的定义域是
满足,即
又分母不为0,则
所以函数的定义域为:
3.A
由题恒成立,所以定义域为R,
,所以为定义在R上的偶函数,
当在单调递减,在单调递增,
所以在单调递减,在单调递增,
在单调递减,在单调递增,,
所以函数在和处均取得最小值,
若函数在开区间上恒有最小值,
则或,
解得:
4.A
由为单调递增函数,
则,
所以,
由为增函数,所以,
所以,
综上所述,.
5.A
设,
当时,单调递增,而在上单调递减,所以单调递减,所以,
当时,单调递增,又单调递减,所以在上单调递减,
当时,单调递减,又单调递减,所以在上单调递增.
6.C
设,
因为,
所以的图象关于直线对称,
设的4个不同的实数根为,
则,
则,
由题意可知,解得,
,
,的最小值为,
作出的大致图象,如图所示:
由图象可知,若关于的方程有4个不同的实数根,
则.
7.D
解:基本事件总数,
所选出的两个数字相差不超过1,基本事件有:
,共有16个.
∴两个小朋友“心有灵犀”的概率为.
故选:D.
8.C
对于A,当时,不是偶函数,错误;
对于B,当,时,函数,满足,但函数的图象不关于直线对称,错误;
对于C,若,则在区间上单调递增,正确;
对于D,若,函数在区间上的最大值不一定是,如时,函数的图象在轴上方,错误.
二、9.AB
由,,
可得,
令,
则,
令,
则,
由,得,
当且仅当时取等号;
所以,
,
所以,
10.ABD
A.函数的定义域为,即,则,∴函数中的取值范围,即定义域为,即定义域是,A正确;
B.令,则,∴图象过定点.B正确;
C.中,它的图象是直线上去掉点,不是直线,C错;
D.时,,不合题意,时,,,∴.D正确.
11.ABC
令,则,
在同一直角坐标系中作出与的图像,
因为函数恰有个零点,
所以只需与有两个交点.
由图可知,为使与有两个交点,
只需或即可,
故当时,两函数均有两个交点,即ABC正确;当时,两函数有三个交点,不满足题意,故D错;
12.ABD
甲省确诊人数的平均数是,
乙省确诊人数的平均数是
所以正确;
甲省确诊人数摆动幅度比乙省大,所以甲省的方差大
所以正确;
甲省确诊人数,中位数是24,
所以错误;
乙省确诊人数,极差是12,
所以正确;
三、13.4
由题意,.
14.
因为为定义在上的奇函数,当时,,
则,解得,则,
所以,因此.
15.
任取一卦的所有可能的结果有8卦,
其中恰有2根阳线和1根阴线包含的基本事件有卦,
所以恰有2根阳线和1根阴线的概率为,
故答案为:
16.
解:令t=f(x),则原函数等价为y=2t2+3mt+1.
作出函数f(x)的图象如图,
图象可知
当t<0时,函数t=f(x)有一个零点.
当t=0时,函数t=f(x)有三个零点.
当0<t<1时,函数t=f(x)有四个零点.
当t=1时,函数t=f(x)有三个零点.
当t>1时,函数t=f(x)有两个零点.
要使关于x的函数y=2f2(x)+3mf(x)+1有6个不同的零点,
则函数y=2t2+3mt+1有两个根t1,t2,
且0<t1<1,t2>1或t1=0,t2=1,
令g(t)=2t2+3mt+1,则由根的分布可得,
将t=1,代入得:m=﹣1,
此时g(t)=2t2﹣3t+1的另一个根为t=,不满足t1=0,t2=1,
若0<t1<1,t2>1,则,
解得:m<﹣1,
三、17.(1)∵的解集为
∴,,
∴.故
从而,解得.
(2)∵恒成立,
∴,
∴∴,
令,∵ ∴,从而,
∴,令.
①当时,;
②当时, ,
∴的最大值为.
18.(1)因为是定义域为R奇函数,
由定义,所以
所以,
∴.
所以
证明:任取,
.
,.
,即.
在定义域上为增函数.
(2)由(1)得是定义域为R奇函数和增函数
所以.
19.解:(1)令,则,故,故函数的解析式;
又,故是奇函数;
当时是增函数,是减函数,故是增函数,而,故在R上是增函数;
当时是减函数,是增函数,故是减函数,而,故在R上是增函数;
综上,在R上是增函数;
(2)移项,由(1)中奇偶性知不等式即,再根据单调性可得,解得,
所以不等式的解集是;
(3)依题意恰在上取负值,结合单调性知时,即,化简得,故.
20.(1)由题意知,当m=0时,x=1(万件),
所以1=3-k k=2,所以x=3- (m≥0),
每件产品的销售价格为1.5× (元),
所以2020年的利润y=1.5x×-8-16x-m
=-+29(m≥0).
(2)因为m≥0时,+(m+1)≥2=8,
所以y≤-8+29=21,当且仅当=m+1 m=3(万元)时,ymax=21(万元).
故该厂家2020年的促销费用投入3万元时,厂家的利润最大为21万元.
21.(1)由,解得.
(2)这组数据的平均数为.
中位数设为,则,解得.
(3)满意度评分值在内有人,其中男生3人,女生2人.记为,
记“满意度评分值为的人中随机抽取2人进行座谈,恰有1名女生”为事件,
从5人中抽取2人有:,,,,, ,,,,
所以总基本事件个数为10个,包含的基本事件个数为3个,
所以 .
22.(1)若,则,
因为当时,都是单调递增的函数,
所以在单调递增,
因为,
所以存在唯一的使得,
所以函数恰有一个正零点;
(2)设,作出函数图象,如图所示:
因为函数恰有三个零点,
所以方程必有两根,
或者,
当时,.
当时,,此时,不符合题意.
综上所述:实数取值范围为.
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知不等式的解集为,则不等式的解集为( )
A. B.C. D.
2.若函数的定义域是,则函数的定义域为( )
A. B. C. D.
3.已知函数,若函数在开区间上恒有最小值,则实数的取值范围为( ).
A. B.
C. D.
4.已知,,,则( )
A. B. C. D.
5.设,函数在上单调递减,则( )
A.在上单调递减,在上单调递增
B.在上单调递增,在上单调递减
C.在上单调递增,在上单调递增
D.在上单调递减,在上单调递减
6.已知函数,若关于的方程有4个不同的实数根,且所有实数根之和为2,则实数的取值范围是( )
A. B. C. D.
7.为了提高幼儿园孩子认识数字的能力,老师任意选取两个小朋友,让他们每人从1,2,3,4,5,6这六个数字当中任选一个数字(两人所选的数字可以相同),如果所选出的两个数字相差不超过1,则称这两个小朋友“心有灵犀”.两个小朋友“心有灵犀”的概率为( )
A. B. C. D.
8.已知函数.下列命题正确的是( )
A.必是偶函数
B.当时,的图像关于直线对称
C.若,则在区间上是增函数
D.有最大值
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对得5分,选对但不全的得3分,有选错的得0分)
9.对任意实数.若不等式恒成立,则实数可取的值为( )
A. B. C. D.
10.给出以下四个结论,其中所有正确结论的序号是( )
A.若函数的定义域为,则函数的定义域是;
B.函数(其中,且)的图象过定点;
C.当时,幂函数的图象是一条直线;
D.若,则的取值范围是.
11.已知函数,若函数恰有个零点,则实数可以是( )
A. B. C. D.
12.在全国人民的共同努力下,特别是医护人员的奋力救治下,“新冠肺炎”疫情得到了有效控制.如图是国家卫健委给出的全国疫情通报,甲、乙两个省份从2月7日到2月13日一周的新增“新冠肺炎”确诊人数的折线图.
则下列关于甲、乙两省新增确诊人数的说法,正确的是( )
A.甲省的平均数比乙省低
B.甲省的方差比乙省大
C.甲省的中位数是27
D.乙省的极差是12
三、填空题(本大题共4小题,每小题5分,共20分,请把正确答案填在题中横线上)
13.计算:_________.
14.设函数为定义在上的奇函数,且当时,(其中为实数),则的值为________.
15.《易经》是中国传统文化中的精髓,下图是易经八卦图(含乾、坤、巽、震、坎、离、艮、兑八卦),每一卦由三根线组成(表示一根阳线,表示一根阴线),从八卦中任取一卦,这一卦的三根线中恰有2根阳线和1根阴线的概率_____.
16.已知函数,若函数有6个不同的零点,则实数m的范围是_______.
四、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明,证明过程或演算步骤)
17.(本小题满分10分)已知二次函数.
(1)若的解集为,解关于x的不等式;
(2)若不等式对恒成立,求的最大值.
19.(本小题满分12分)已知函数为奇函数.
(1)求实数a的值并证明是增函数;
(2)若实数满足不等式,求t的取值范围.
20.(本小题满分12分)已知且,.
(1)求函数的解析式,并判断其奇偶性和单调性;
(2)当的定义域为时,解关于的不等式
(3)若恰在上取负值,求的值.
21.(本小题满分12分)某厂家拟定在2020年举行促销活动,经调查测算,该产品的年销量(即该厂的年产量)x万件与年促销费用m(m≥0)万元满足x=3- (k为常数).如果不搞促销活动,那么该产品的年销量只能是1万件.已知2020年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
(1)将2020年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2020年的促销费用投入多少万元时,厂家利润最大?
22.(本小题满分12分)某城市交通部门为了对该城市共享单车加强监管,随机选取了100人就该城市共享单车的推行情况进行问卷调查,并将问卷中的这100人根据其满意度评分值(百分制)按照分成5组,制成如图所示频率分直方图.
(1)求图中的值;
(2)求这组数据的平均数和中位数;
(3)已知满意度评分值在内的男生数与女生数的比为3:2,若在满意度评分值为的人中随机抽取2人进行座谈,求2人均为男生的概率.
23.(本小题满分12分)已知函数
(1)若,求证:函数恰有一个正零点;(用图像法证明不给分)
(2)若函数恰有三个零点,求实数取值范围.
试卷第1页,总3页
参考答案
1.C
不等式的解集为,
和2是方程的两个根,且,
, 可得,
则不等式等价于,
即,解得或,
故不等式的解集为.
2.C
函数的定义域是
满足,即
又分母不为0,则
所以函数的定义域为:
3.A
由题恒成立,所以定义域为R,
,所以为定义在R上的偶函数,
当在单调递减,在单调递增,
所以在单调递减,在单调递增,
在单调递减,在单调递增,,
所以函数在和处均取得最小值,
若函数在开区间上恒有最小值,
则或,
解得:
4.A
由为单调递增函数,
则,
所以,
由为增函数,所以,
所以,
综上所述,.
5.A
设,
当时,单调递增,而在上单调递减,所以单调递减,所以,
当时,单调递增,又单调递减,所以在上单调递减,
当时,单调递减,又单调递减,所以在上单调递增.
6.C
设,
因为,
所以的图象关于直线对称,
设的4个不同的实数根为,
则,
则,
由题意可知,解得,
,
,的最小值为,
作出的大致图象,如图所示:
由图象可知,若关于的方程有4个不同的实数根,
则.
7.D
解:基本事件总数,
所选出的两个数字相差不超过1,基本事件有:
,共有16个.
∴两个小朋友“心有灵犀”的概率为.
故选:D.
8.C
对于A,当时,不是偶函数,错误;
对于B,当,时,函数,满足,但函数的图象不关于直线对称,错误;
对于C,若,则在区间上单调递增,正确;
对于D,若,函数在区间上的最大值不一定是,如时,函数的图象在轴上方,错误.
二、9.AB
由,,
可得,
令,
则,
令,
则,
由,得,
当且仅当时取等号;
所以,
,
所以,
10.ABD
A.函数的定义域为,即,则,∴函数中的取值范围,即定义域为,即定义域是,A正确;
B.令,则,∴图象过定点.B正确;
C.中,它的图象是直线上去掉点,不是直线,C错;
D.时,,不合题意,时,,,∴.D正确.
11.ABC
令,则,
在同一直角坐标系中作出与的图像,
因为函数恰有个零点,
所以只需与有两个交点.
由图可知,为使与有两个交点,
只需或即可,
故当时,两函数均有两个交点,即ABC正确;当时,两函数有三个交点,不满足题意,故D错;
12.ABD
甲省确诊人数的平均数是,
乙省确诊人数的平均数是
所以正确;
甲省确诊人数摆动幅度比乙省大,所以甲省的方差大
所以正确;
甲省确诊人数,中位数是24,
所以错误;
乙省确诊人数,极差是12,
所以正确;
三、13.4
由题意,.
14.
因为为定义在上的奇函数,当时,,
则,解得,则,
所以,因此.
15.
任取一卦的所有可能的结果有8卦,
其中恰有2根阳线和1根阴线包含的基本事件有卦,
所以恰有2根阳线和1根阴线的概率为,
故答案为:
16.
解:令t=f(x),则原函数等价为y=2t2+3mt+1.
作出函数f(x)的图象如图,
图象可知
当t<0时,函数t=f(x)有一个零点.
当t=0时,函数t=f(x)有三个零点.
当0<t<1时,函数t=f(x)有四个零点.
当t=1时,函数t=f(x)有三个零点.
当t>1时,函数t=f(x)有两个零点.
要使关于x的函数y=2f2(x)+3mf(x)+1有6个不同的零点,
则函数y=2t2+3mt+1有两个根t1,t2,
且0<t1<1,t2>1或t1=0,t2=1,
令g(t)=2t2+3mt+1,则由根的分布可得,
将t=1,代入得:m=﹣1,
此时g(t)=2t2﹣3t+1的另一个根为t=,不满足t1=0,t2=1,
若0<t1<1,t2>1,则,
解得:m<﹣1,
三、17.(1)∵的解集为
∴,,
∴.故
从而,解得.
(2)∵恒成立,
∴,
∴∴,
令,∵ ∴,从而,
∴,令.
①当时,;
②当时, ,
∴的最大值为.
18.(1)因为是定义域为R奇函数,
由定义,所以
所以,
∴.
所以
证明:任取,
.
,.
,即.
在定义域上为增函数.
(2)由(1)得是定义域为R奇函数和增函数
所以.
19.解:(1)令,则,故,故函数的解析式;
又,故是奇函数;
当时是增函数,是减函数,故是增函数,而,故在R上是增函数;
当时是减函数,是增函数,故是减函数,而,故在R上是增函数;
综上,在R上是增函数;
(2)移项,由(1)中奇偶性知不等式即,再根据单调性可得,解得,
所以不等式的解集是;
(3)依题意恰在上取负值,结合单调性知时,即,化简得,故.
20.(1)由题意知,当m=0时,x=1(万件),
所以1=3-k k=2,所以x=3- (m≥0),
每件产品的销售价格为1.5× (元),
所以2020年的利润y=1.5x×-8-16x-m
=-+29(m≥0).
(2)因为m≥0时,+(m+1)≥2=8,
所以y≤-8+29=21,当且仅当=m+1 m=3(万元)时,ymax=21(万元).
故该厂家2020年的促销费用投入3万元时,厂家的利润最大为21万元.
21.(1)由,解得.
(2)这组数据的平均数为.
中位数设为,则,解得.
(3)满意度评分值在内有人,其中男生3人,女生2人.记为,
记“满意度评分值为的人中随机抽取2人进行座谈,恰有1名女生”为事件,
从5人中抽取2人有:,,,,, ,,,,
所以总基本事件个数为10个,包含的基本事件个数为3个,
所以 .
22.(1)若,则,
因为当时,都是单调递增的函数,
所以在单调递增,
因为,
所以存在唯一的使得,
所以函数恰有一个正零点;
(2)设,作出函数图象,如图所示:
因为函数恰有三个零点,
所以方程必有两根,
或者,
当时,.
当时,,此时,不符合题意.
综上所述:实数取值范围为.
同课章节目录
- 第一章 预备知识
- 1 集合
- 2 常用逻辑用语
- 3 不等式
- 4 一元二次函数与一元二次不等式
- 第二章 函数
- 1 生活中的变量关系
- 2 函数
- 3 函数的单调性和最值
- 4 函数的奇偶性与简单的幂函数
- 第三章 指数运算与指数函数
- 1 指数幂的拓展
- 2 指数幂的运算性质
- 3 指数函数
- 第四章 对数运算和对数函数
- 1 对数的概念
- 2 对数的运算
- 3 对数函数
- 4 指数函数、幂函数、对数函数增长的比较
- 5 信息技术支持的函数研究
- 第五章 函数应用
- 1 方程解的存在性及方程的近似解
- 2 实际问题中的函数模型
- 第六章 统计
- 1 获取数据的途径
- 2 抽样的基本方法
- 3 用样本估计总体分布
- 4 用样本估计总体数字特征
- 第七章 概率
- 1 随机现象与随机事件
- 2 古典概型
- 3 频率与概率
- 4 事件的独立性
- 第八章 数学建模活动(一)
- 1 走进数学建模
- 2 数学建模的主要步骤
- 3 数学建模活动的主要过程
