湖北省武汉市重点中学2014-2015学年高一12月月考数学试题
文档属性
| 名称 | 湖北省武汉市重点中学2014-2015学年高一12月月考数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 124.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-25 14:39:26 | ||
图片预览


文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
2017届高一年级12月月考
数学试卷
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的的四个选项中,只有一项是符合题目要求的。21cnjy.com
1.已知集合,则 ( A )
A. B. C. D.
2、已知扇形的周长是,面积是,则扇形的中心角的弧度数是( B )
A.1 B.4 C.1或4 D.2或4
3、已知函数f (x)=asinx+btanx+1,满足f (5)=7,则f (-5)的值为( B )
A.5 B.-5 C.6 D.-6www.21-cn-jy.com
4、下列说法正确的个数是( B )
①正切函数在定义域上单调递增;
②函数在区间上满足,则函数在上有零点;
③的图象关于原点对称;
④若一个函数是周期函数,那么它一定有最小正周期。
A.0个 B.1个 C.2个 D.3个
5.一种放射性元素,最初的质量为500 ( http: / / www.21cnjy.com )g,按每年10%衰减.则这种放射性元素的半衰期为(注:剩留量为最初质量的一半所需的时间叫做半衰期).(精确到0.1.已知lg2=0.3010,lg3=0.4771) ( B )
A.5.2 B.6.6 C.7.1 D.8.3【来源:21·世纪·教育·网】
6、若为锐角三角形,则下列式子一定成立的是 ( D )
A. B. C. D.
7.已知 的值为 ( D )
A.-2 B.2 C. D.-
8.已知=-,那么的值是( A )
A. B.- C.2 D.-2
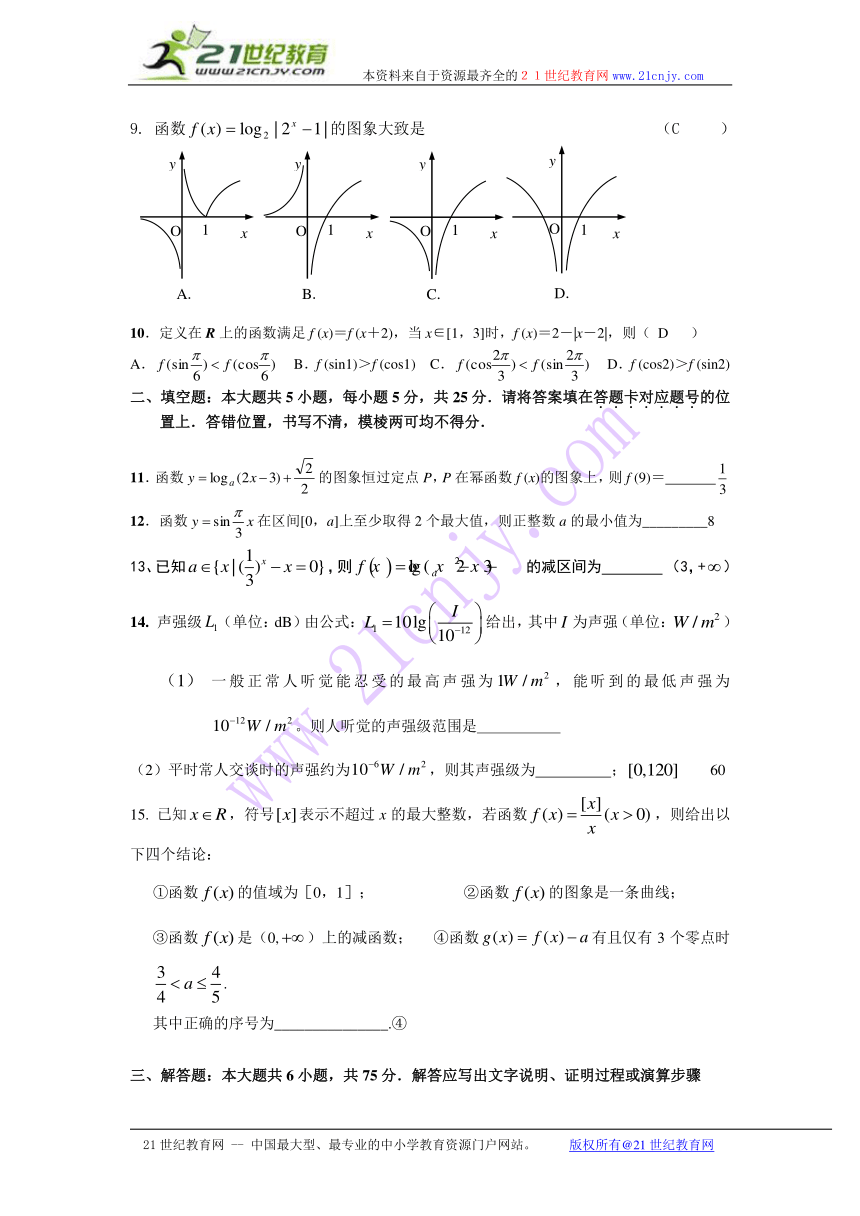
9. 函数的图象大致是 (C )
10.定义在R上的函数满足f (x)=f (x+2),当x∈[1,3]时,f (x)=2-|x-2|,则( D )
A. B.f (sin1)>f (cos1) C. D.f (cos2)>f (sin2)
二、填空题:本大题共5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,模棱两可均不得分.21·cn·jy·com
11.函数的图象恒过定点P,P在幂函数f (x)的图象上,则f (9)=
12.函数在区间[0,a]上至少取得2个最大值,则正整数a的最小值为_________8
13、已知,则的减区间为 (3,+)
14. 声强级(单位:dB)由公式:给出,其中为声强(单位:)
(1) 一般正常人听觉能忍受的最高声强为,能听到的最低声强为。则人听觉的声强级范围是 2·1·c·n·j·y
(2)平时常人交谈时的声强约为,则其声强级为 ; 60
15. 已知,符号表示不超过x的最大整数,若函数,则给出以下四个结论:
①函数的值域为[0,1]; ②函数的图象是一条曲线;
③函数是(0,)上的减函数; ④函数有且仅有3个零点时.
其中正确的序号为_______________.④
三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤
16. 已知函数f(x)=的定义域为A, 关于x的不等式22ax<2a+x的解集为B, 求使A∩B=A的实数a的取值范围. 21·世纪*教育网
解:由, 即…………2分
由……………………………3分
又………………………………………5分
故①当时(*)式即 有,此时…………7分
②当时(*)式满足…………9分
③当时(*)式即 有,此时;…11分
综合①②③可知:……………………………………………………………………12分
另解:(*)式 记………………………………………8分
由可知, 对 恒成立………………………………………………10分
…………………………………………………………………………12分
17. (本小题满分12分)
(1)已知角的终边上有一点,且,求;
(2)已知函数,设,求的值。
18.函数()的最大值为3, 其图像相邻两条对称轴之间的距离为,
(1)求函数的解析式; (2)求函数的对称中心的坐标,
(3)设,则,求的值.
(2)
19. (12分)“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度(单位:千克/年)是养殖密度(单位:尾/立方米)的函数.当不超过4(尾/立方米)时,的值为(千克/年);当时,是的一次函数;当达到(尾/立方米)时,因缺氧等原因,的值为(千克/年)。21教育网
(1)当时,求函数的表达式;
(2)当养殖密度为多大时,鱼的年生长量(单位:千克/立方米)可以达到最大,并求出最大值.
解:(1)由题意:当时,;
当时,设,显然在是减函数,
由已知得,解得
故函数= ( http: / / www.21cnjy.com )
(2)依题意并由(1)可得 ( http: / / www.21cnjy.com )
当时,为增函数,故;
当时,,
.
所以,当时,的最大值为.
当养殖密度为10尾/立方米时,鱼的年生长量可以达到最大,最大值约为千克/立方米.
20.已知指数函数满足:g(2)=4,定义域为的函数是奇函数。
(1)确定的解析式;(2)求m,n的值;
(3)若对任意的,不等式恒成立,
求实数的取值范围。
解:(1)y=g(x)=2x;
(2)由(1)知:,因为f(x)是奇函数,所以f(0)=0,即,
∴,又由f(1)=-f(-1)知,
∴m=2,n=1。
(3)由(2)知,,易知f(x)在(-∞,+∞)上为减函数,
又因f(x)是奇函数,从而不等式:等价于,因f(x)为减函数,由上式推得:,
即对一切t∈R有:,从而判别式,
∴实数k的取值范围是(-∞,)。www-2-1-cnjy-com
21.设角α∈(0,),f (x)的定义域为[0,1],f (0)=0,f (1)=1,当x≥y时,有=f (x)sinα+(1-sinα)f (y)2-1-c-n-j-y
(1) 求、的值;(2) 求α的值;(3) 设g(x)=4sin(2x+α)-1,且lgg(x)>0,求g(x)的单调区间21世纪教育网版权所有
(1)
(2)
∴sinα=3sin2α-2sin3α,解得sinα=0或sinα=1或sinα=
∵α∈(0,),∴sinα=,α=
(3) ∵lgg(x)>0,∴g(x)>1,sin(2x+)>,+2kπ≤2x+≤+2kπ,k∈Z
由函数图象可知,g(x)的递增区间为+2kπ≤2x+≤+2kπ,kπ≤x≤+kπ,k∈Z
g(x)的递减区间为+2kπ≤2x+≤+2kπ,+kπ≤x≤+kπ,k∈Z
x
y
O
1
D.
x
y
O
1
C.
x
y
O
1
B.
x
y
O
1
A.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
2017届高一年级12月月考
数学试卷
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的的四个选项中,只有一项是符合题目要求的。21cnjy.com
1.已知集合,则 ( A )
A. B. C. D.
2、已知扇形的周长是,面积是,则扇形的中心角的弧度数是( B )
A.1 B.4 C.1或4 D.2或4
3、已知函数f (x)=asinx+btanx+1,满足f (5)=7,则f (-5)的值为( B )
A.5 B.-5 C.6 D.-6www.21-cn-jy.com
4、下列说法正确的个数是( B )
①正切函数在定义域上单调递增;
②函数在区间上满足,则函数在上有零点;
③的图象关于原点对称;
④若一个函数是周期函数,那么它一定有最小正周期。
A.0个 B.1个 C.2个 D.3个
5.一种放射性元素,最初的质量为500 ( http: / / www.21cnjy.com )g,按每年10%衰减.则这种放射性元素的半衰期为(注:剩留量为最初质量的一半所需的时间叫做半衰期).(精确到0.1.已知lg2=0.3010,lg3=0.4771) ( B )
A.5.2 B.6.6 C.7.1 D.8.3【来源:21·世纪·教育·网】
6、若为锐角三角形,则下列式子一定成立的是 ( D )
A. B. C. D.
7.已知 的值为 ( D )
A.-2 B.2 C. D.-
8.已知=-,那么的值是( A )
A. B.- C.2 D.-2
9. 函数的图象大致是 (C )
10.定义在R上的函数满足f (x)=f (x+2),当x∈[1,3]时,f (x)=2-|x-2|,则( D )
A. B.f (sin1)>f (cos1) C. D.f (cos2)>f (sin2)
二、填空题:本大题共5小题,每小题5分,共25分.请将答案填在答题卡对应题号的位置上.答错位置,书写不清,模棱两可均不得分.21·cn·jy·com
11.函数的图象恒过定点P,P在幂函数f (x)的图象上,则f (9)=
12.函数在区间[0,a]上至少取得2个最大值,则正整数a的最小值为_________8
13、已知,则的减区间为 (3,+)
14. 声强级(单位:dB)由公式:给出,其中为声强(单位:)
(1) 一般正常人听觉能忍受的最高声强为,能听到的最低声强为。则人听觉的声强级范围是 2·1·c·n·j·y
(2)平时常人交谈时的声强约为,则其声强级为 ; 60
15. 已知,符号表示不超过x的最大整数,若函数,则给出以下四个结论:
①函数的值域为[0,1]; ②函数的图象是一条曲线;
③函数是(0,)上的减函数; ④函数有且仅有3个零点时.
其中正确的序号为_______________.④
三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤
16. 已知函数f(x)=的定义域为A, 关于x的不等式22ax<2a+x的解集为B, 求使A∩B=A的实数a的取值范围. 21·世纪*教育网
解:由, 即…………2分
由……………………………3分
又………………………………………5分
故①当时(*)式即 有,此时…………7分
②当时(*)式满足…………9分
③当时(*)式即 有,此时;…11分
综合①②③可知:……………………………………………………………………12分
另解:(*)式 记………………………………………8分
由可知, 对 恒成立………………………………………………10分
…………………………………………………………………………12分
17. (本小题满分12分)
(1)已知角的终边上有一点,且,求;
(2)已知函数,设,求的值。
18.函数()的最大值为3, 其图像相邻两条对称轴之间的距离为,
(1)求函数的解析式; (2)求函数的对称中心的坐标,
(3)设,则,求的值.
(2)
19. (12分)“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度(单位:千克/年)是养殖密度(单位:尾/立方米)的函数.当不超过4(尾/立方米)时,的值为(千克/年);当时,是的一次函数;当达到(尾/立方米)时,因缺氧等原因,的值为(千克/年)。21教育网
(1)当时,求函数的表达式;
(2)当养殖密度为多大时,鱼的年生长量(单位:千克/立方米)可以达到最大,并求出最大值.
解:(1)由题意:当时,;
当时,设,显然在是减函数,
由已知得,解得
故函数= ( http: / / www.21cnjy.com )
(2)依题意并由(1)可得 ( http: / / www.21cnjy.com )
当时,为增函数,故;
当时,,
.
所以,当时,的最大值为.
当养殖密度为10尾/立方米时,鱼的年生长量可以达到最大,最大值约为千克/立方米.
20.已知指数函数满足:g(2)=4,定义域为的函数是奇函数。
(1)确定的解析式;(2)求m,n的值;
(3)若对任意的,不等式恒成立,
求实数的取值范围。
解:(1)y=g(x)=2x;
(2)由(1)知:,因为f(x)是奇函数,所以f(0)=0,即,
∴,又由f(1)=-f(-1)知,
∴m=2,n=1。
(3)由(2)知,,易知f(x)在(-∞,+∞)上为减函数,
又因f(x)是奇函数,从而不等式:等价于,因f(x)为减函数,由上式推得:,
即对一切t∈R有:,从而判别式,
∴实数k的取值范围是(-∞,)。www-2-1-cnjy-com
21.设角α∈(0,),f (x)的定义域为[0,1],f (0)=0,f (1)=1,当x≥y时,有=f (x)sinα+(1-sinα)f (y)2-1-c-n-j-y
(1) 求、的值;(2) 求α的值;(3) 设g(x)=4sin(2x+α)-1,且lgg(x)>0,求g(x)的单调区间21世纪教育网版权所有
(1)
(2)
∴sinα=3sin2α-2sin3α,解得sinα=0或sinα=1或sinα=
∵α∈(0,),∴sinα=,α=
(3) ∵lgg(x)>0,∴g(x)>1,sin(2x+)>,+2kπ≤2x+≤+2kπ,k∈Z
由函数图象可知,g(x)的递增区间为+2kπ≤2x+≤+2kπ,kπ≤x≤+kπ,k∈Z
g(x)的递减区间为+2kπ≤2x+≤+2kπ,+kπ≤x≤+kπ,k∈Z
x
y
O
1
D.
x
y
O
1
C.
x
y
O
1
B.
x
y
O
1
A.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
