山东省跃华学校2014-2015学年高一1月月考数学试题(无答案)
文档属性
| 名称 | 山东省跃华学校2014-2015学年高一1月月考数学试题(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 85.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-01-14 08:51:46 | ||
图片预览

文档简介
跃华学校2014-2015学年第一学期月考考试
高一(数学)试题
命题人 :陈祥和 审核:李丹丹 考试时间:120分钟 (总分150分)日期:2015、1
(第I卷)
一、选择题(本大题共10小题,每小题5分,共50分)
1、(2012·广东)设集合U={1,2,3,4,5,6},M={1,2,4},则?UM等于 ( )
A.U B.{1,3,5} C.{3,5,6} D.{2,4,6}
2、将参加英语口语测试的1 000名学生编号为000,001,002,…,999,从中抽取一个容量为50的样本,按系统抽样的方法分为50组,如果第一组编号为000,001,002,…,019,且第一组随机抽取的编号为015,则抽取的第35个编号为( )
A.700 B.669 C. 676 D.695
3、如图所示,在一个边长为2的正方形中随机撒入200粒豆子,恰有120
粒落在阴影区域内,则该阴影部分的面积约为( )
A. B. C. D.
4、(2011·重庆)从一堆苹果中任取10只,称得它们的质量如下(单位:克):125 120 122 105 130 114 116 95 120 134则样本数据落在[114.5,124.5]内的频率为( )
A.0.2 B.0.3 C.0.4 D.0.5
5、右图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个位数字,从图中可以得到这10位同学身高的中
位数是 ( )
A.161 cm B.162 cm C.163 cm D.164 cm
6、(2012·江西)已知函数f(x)=,则f(f(3))等于 ( )
A. B.3 C. D.
7、(2012·安徽)(log29)·(log34)等于( )
A. 4 B. 2 C. D.
8、给定函数①,②,③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是 ( )
A.①② B.②③ C.③④ D.①④
9、下列与的终边相同的角的表达式中正确的是 ( )
A.2kπ+45° (k∈Z) B.k·360°+π (k∈Z)
C.k·360°-315°(k∈Z) D.kπ+ (k∈Z)
10、函数f(x)=2x+3x的零点所在的一个区间是 ( )
A.(-2,-1) B.(-1,0) C.(0,1) D.(1,2)
第Ⅱ卷(非选择题,共100分)
二、填空题:(本大题共5小题,每小题5分,共25分)
11、 已知x、y的取值如下表:
x
0
1
3
4
y
2.2
4.3
4.8
6.7
从所得的散点图分析,y与x线性相关,且 =0.95x+ ,则 =________.
12、函数的定义域为 。
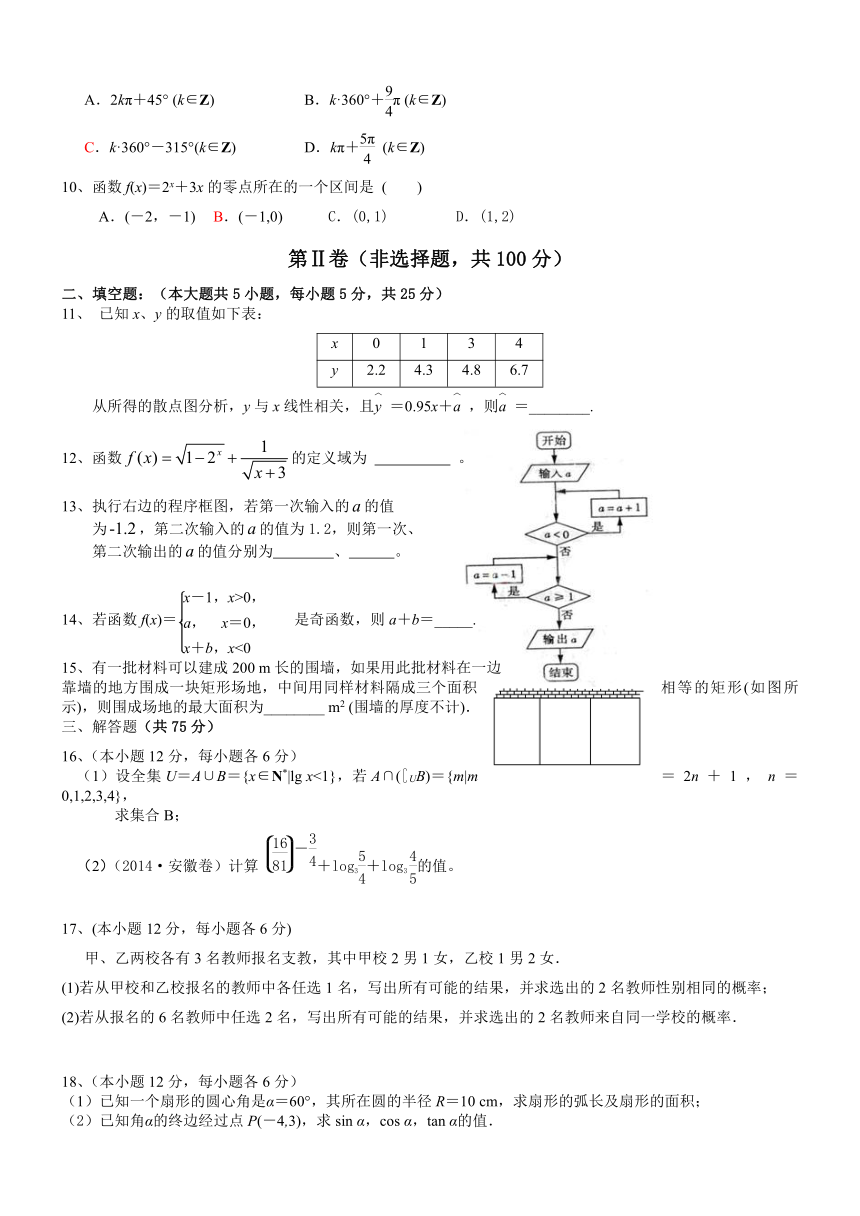
13、执行右边的程序框图,若第一次输入的的值
为,第二次输入的的值为1.2,则第一次、
第二次输出的的值分别为 、 。
14、若函数f(x)=是奇函数,则a+b=_____.
15、有一批材料可以建成200 m长的围墙,如果用此批材料在一边
靠墙的地方围成一块矩形场地,中间用同样材料隔成三个面积相等的矩形(如图所示),则围成场地的最大面积为________ m2 (围墙的厚度不计).
三、解答题(共75分)
16、(本小题12分,每小题各6分)
(1)设全集U=A∪B={x∈N*|lg x<1},若A∩(?UB)={m|m=2n+1,n=0,1,2,3,4},
求集合B;
(2)(2014·安徽卷)计算 +log3+log3的值。
17、(本小题12分,每小题各6分)
甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女.
(1)若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率;
(2)若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率.
18、(本小题12分,每小题各6分)
(1)已知一个扇形的圆心角是α=60°,其所在圆的半径R=10 cm,求扇形的弧长及扇形的面积;
(2)已知角α的终边经过点P(-4,3),求sin α,cos α,tan α的值.
19、(本题共13分,(1)3分;(2)5分;(3)5分)
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分
(每组成绩取中间值);
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.
分数段
[50,60)
[60,70)
[70,80)
[80,90)
x∶y
1∶1
2∶1
3∶4
4∶5
20、(本题共13分,(1)3分;(2)3分;(3)4分;(4)3分)
设函数f(x)=x2-2|x|-1(-3≤x≤3)
(1)证明f(x)是偶函数;
(2)画出这个函数的图象(直接画图,不写过程);
(3)指出函数f(x)的单调区间,并说明在各个单调区间上f(x)是增函数还是减函数;
(4)求函数的值域.
21、(本题共13分,(1)6分;(2)7分)
已知函数f(x)=,x∈[1,+∞).
(1)当a=时,证明函数f(x) 在[1,+∞)上的单调增函数,并求函数f(x)的最小值;
(2)若对任意x∈[1,+∞),f(x)>0恒成立,试求实数a的取值范围.
答案:
1-10 CDBCB DABCB
11、答案 2.6; 12、答案(-3,0]; 13、0.8,0.2; 14、1;15、2 500 m2
16(1)解析 A∪B={x∈N*|lg x<1}={1,2,3,4,5,6,7,8,9},A∩(?UB)={1,3,5,7,9},
∴B={2,4,6,8}.
(2) [解析] 原式= +log3==.
17、解 (1)甲校两男教师分别用A、B表示,女教师用C表示;乙校男教师用D表示,两女教师分别用E、F表示.
从甲校和乙校报名的教师中各任选1名的所有可能的结果为(A,D),(A,E),(A,F),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F)共9种.
从中选出的两名教师性别相同的结果有(A,D),(B,D),(C,E),(C,F)共4种.
故选出的两名教师性别相同的概率为P1=.
(2)从甲校和乙校报名的教师中任选2名的所有可能的结果为(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共15种.
从中选出的两名教师来自同一学校的结果有(A,B),(A,C),(B,C),(D,E),(D,F),(E,F)共6种.
故选出的两名教师来自同一学校的概率为P2==.
18、(1);
(2)。
19解 (1)由频率分布直方图知(2a+0.02+0.03+0.04)×10=1,解得a=0.005.
(2)由频率分布直方图知这100名学生语文成绩的平均分为55×0.005×10+65×0.04×10+75×0.03×10+85×0.02×10+95×0.005×10=73(分).
(3)由频率分布直方图知语文成绩在[50,60),[60,70),[70,80),[80,90)各分数段的人数依次为0.005×10×100=5, 0.04×10×100=40,
0.03×10×100=30, 0.02×10×100=20.
由题中给出的比例关系知数学成绩在上述各分数段的人数依次为5,40×=20,30×=40,20×=25. 故数学成绩在[50,90)之外的人数为100-(5+20+40+25)=10.
20.解 (1)f(-x)=(-x)2-2|-x|-1
=x2-2|x|-1=f(x),
即f(-x)=f(x).∴f(x)是偶函数.
(2)当x≥0时,f(x)=x2-2x-1=(x-1)2-2,
当x<0时,f(x)=x2+2x-1=(x+1)2-2,
即f(x)=
根据二次函数的作图方法,可得函数图象如下图.
(3)由(2)中函数图象可知,函数f(x)的单调区间为[-3,-1],[-1,0],[0,1],[1,3].
f(x)在区间[-3,-1]和[0,1]上为减函数,在[-1,0],[1,3]上为增函数.
(4)当x≥0时,函数f(x)=(x-1)2-2的最小值为-2,最大值为f(3)=2;
当x<0时,函数f(x)=(x+1)2-2的最小值为-2,最大值为f(-3)=2;
故函数f(x)的值域为[-2,2].
21、解(1)当a=时,f(x)=x++2,
设x1,x2∈[1,+∞)且x1f(x1)-f(x2)=x1+-x2-
=(x1-x2)(1-)
∵x1∴1->0,
∴f(x1)-f(x2)<0,∴f(x1)∴f(x)在区间[1,+∞)上为增函数,
∴f(x)在区间[1,+∞)上的最小值为f(1)=.
(2)方法一 f(x)=x++2,x∈[1,+∞),
当a≥0时,函数f(x)的值恒为正,满足题意,当a<0时,函数f(x)递增;
当x=1时,f(x)min=3+a,于是当且仅当f(x)min=3+a>0时,函数f(x)>0恒成立,
故a>-3.
方法二 在区间[1,+∞)上f(x)=>0恒成立等价于x2+2x+a>0恒成立.
即a>-x2-2x恒成立.
又∵x∈[1,+∞),a>-x2-2x恒成立,
∴a应大于函数u=-x2-2x,x∈[1,+∞)的最大值.
∴a>-x2-2x=-(x+1)2+1.
当x=1时,u取得最大值-3,∴a>-3.
高一(数学)试题
命题人 :陈祥和 审核:李丹丹 考试时间:120分钟 (总分150分)日期:2015、1
(第I卷)
一、选择题(本大题共10小题,每小题5分,共50分)
1、(2012·广东)设集合U={1,2,3,4,5,6},M={1,2,4},则?UM等于 ( )
A.U B.{1,3,5} C.{3,5,6} D.{2,4,6}
2、将参加英语口语测试的1 000名学生编号为000,001,002,…,999,从中抽取一个容量为50的样本,按系统抽样的方法分为50组,如果第一组编号为000,001,002,…,019,且第一组随机抽取的编号为015,则抽取的第35个编号为( )
A.700 B.669 C. 676 D.695
3、如图所示,在一个边长为2的正方形中随机撒入200粒豆子,恰有120
粒落在阴影区域内,则该阴影部分的面积约为( )
A. B. C. D.
4、(2011·重庆)从一堆苹果中任取10只,称得它们的质量如下(单位:克):125 120 122 105 130 114 116 95 120 134则样本数据落在[114.5,124.5]内的频率为( )
A.0.2 B.0.3 C.0.4 D.0.5
5、右图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个位数字,从图中可以得到这10位同学身高的中
位数是 ( )
A.161 cm B.162 cm C.163 cm D.164 cm
6、(2012·江西)已知函数f(x)=,则f(f(3))等于 ( )
A. B.3 C. D.
7、(2012·安徽)(log29)·(log34)等于( )
A. 4 B. 2 C. D.
8、给定函数①,②,③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是 ( )
A.①② B.②③ C.③④ D.①④
9、下列与的终边相同的角的表达式中正确的是 ( )
A.2kπ+45° (k∈Z) B.k·360°+π (k∈Z)
C.k·360°-315°(k∈Z) D.kπ+ (k∈Z)
10、函数f(x)=2x+3x的零点所在的一个区间是 ( )
A.(-2,-1) B.(-1,0) C.(0,1) D.(1,2)
第Ⅱ卷(非选择题,共100分)
二、填空题:(本大题共5小题,每小题5分,共25分)
11、 已知x、y的取值如下表:
x
0
1
3
4
y
2.2
4.3
4.8
6.7
从所得的散点图分析,y与x线性相关,且 =0.95x+ ,则 =________.
12、函数的定义域为 。
13、执行右边的程序框图,若第一次输入的的值
为,第二次输入的的值为1.2,则第一次、
第二次输出的的值分别为 、 。
14、若函数f(x)=是奇函数,则a+b=_____.
15、有一批材料可以建成200 m长的围墙,如果用此批材料在一边
靠墙的地方围成一块矩形场地,中间用同样材料隔成三个面积相等的矩形(如图所示),则围成场地的最大面积为________ m2 (围墙的厚度不计).
三、解答题(共75分)
16、(本小题12分,每小题各6分)
(1)设全集U=A∪B={x∈N*|lg x<1},若A∩(?UB)={m|m=2n+1,n=0,1,2,3,4},
求集合B;
(2)(2014·安徽卷)计算 +log3+log3的值。
17、(本小题12分,每小题各6分)
甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女.
(1)若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率;
(2)若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率.
18、(本小题12分,每小题各6分)
(1)已知一个扇形的圆心角是α=60°,其所在圆的半径R=10 cm,求扇形的弧长及扇形的面积;
(2)已知角α的终边经过点P(-4,3),求sin α,cos α,tan α的值.
19、(本题共13分,(1)3分;(2)5分;(3)5分)
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分
(每组成绩取中间值);
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.
分数段
[50,60)
[60,70)
[70,80)
[80,90)
x∶y
1∶1
2∶1
3∶4
4∶5
20、(本题共13分,(1)3分;(2)3分;(3)4分;(4)3分)
设函数f(x)=x2-2|x|-1(-3≤x≤3)
(1)证明f(x)是偶函数;
(2)画出这个函数的图象(直接画图,不写过程);
(3)指出函数f(x)的单调区间,并说明在各个单调区间上f(x)是增函数还是减函数;
(4)求函数的值域.
21、(本题共13分,(1)6分;(2)7分)
已知函数f(x)=,x∈[1,+∞).
(1)当a=时,证明函数f(x) 在[1,+∞)上的单调增函数,并求函数f(x)的最小值;
(2)若对任意x∈[1,+∞),f(x)>0恒成立,试求实数a的取值范围.
答案:
1-10 CDBCB DABCB
11、答案 2.6; 12、答案(-3,0]; 13、0.8,0.2; 14、1;15、2 500 m2
16(1)解析 A∪B={x∈N*|lg x<1}={1,2,3,4,5,6,7,8,9},A∩(?UB)={1,3,5,7,9},
∴B={2,4,6,8}.
(2) [解析] 原式= +log3==.
17、解 (1)甲校两男教师分别用A、B表示,女教师用C表示;乙校男教师用D表示,两女教师分别用E、F表示.
从甲校和乙校报名的教师中各任选1名的所有可能的结果为(A,D),(A,E),(A,F),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F)共9种.
从中选出的两名教师性别相同的结果有(A,D),(B,D),(C,E),(C,F)共4种.
故选出的两名教师性别相同的概率为P1=.
(2)从甲校和乙校报名的教师中任选2名的所有可能的结果为(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共15种.
从中选出的两名教师来自同一学校的结果有(A,B),(A,C),(B,C),(D,E),(D,F),(E,F)共6种.
故选出的两名教师来自同一学校的概率为P2==.
18、(1);
(2)。
19解 (1)由频率分布直方图知(2a+0.02+0.03+0.04)×10=1,解得a=0.005.
(2)由频率分布直方图知这100名学生语文成绩的平均分为55×0.005×10+65×0.04×10+75×0.03×10+85×0.02×10+95×0.005×10=73(分).
(3)由频率分布直方图知语文成绩在[50,60),[60,70),[70,80),[80,90)各分数段的人数依次为0.005×10×100=5, 0.04×10×100=40,
0.03×10×100=30, 0.02×10×100=20.
由题中给出的比例关系知数学成绩在上述各分数段的人数依次为5,40×=20,30×=40,20×=25. 故数学成绩在[50,90)之外的人数为100-(5+20+40+25)=10.
20.解 (1)f(-x)=(-x)2-2|-x|-1
=x2-2|x|-1=f(x),
即f(-x)=f(x).∴f(x)是偶函数.
(2)当x≥0时,f(x)=x2-2x-1=(x-1)2-2,
当x<0时,f(x)=x2+2x-1=(x+1)2-2,
即f(x)=
根据二次函数的作图方法,可得函数图象如下图.
(3)由(2)中函数图象可知,函数f(x)的单调区间为[-3,-1],[-1,0],[0,1],[1,3].
f(x)在区间[-3,-1]和[0,1]上为减函数,在[-1,0],[1,3]上为增函数.
(4)当x≥0时,函数f(x)=(x-1)2-2的最小值为-2,最大值为f(3)=2;
当x<0时,函数f(x)=(x+1)2-2的最小值为-2,最大值为f(-3)=2;
故函数f(x)的值域为[-2,2].
21、解(1)当a=时,f(x)=x++2,
设x1,x2∈[1,+∞)且x1
=(x1-x2)(1-)
∵x1
∴f(x1)-f(x2)<0,∴f(x1)
∴f(x)在区间[1,+∞)上的最小值为f(1)=.
(2)方法一 f(x)=x++2,x∈[1,+∞),
当a≥0时,函数f(x)的值恒为正,满足题意,当a<0时,函数f(x)递增;
当x=1时,f(x)min=3+a,于是当且仅当f(x)min=3+a>0时,函数f(x)>0恒成立,
故a>-3.
方法二 在区间[1,+∞)上f(x)=>0恒成立等价于x2+2x+a>0恒成立.
即a>-x2-2x恒成立.
又∵x∈[1,+∞),a>-x2-2x恒成立,
∴a应大于函数u=-x2-2x,x∈[1,+∞)的最大值.
∴a>-x2-2x=-(x+1)2+1.
当x=1时,u取得最大值-3,∴a>-3.
同课章节目录
