初三数学圆的有关计算(广东省深圳市南山区)(无答案)
文档属性
| 名称 | 初三数学圆的有关计算(广东省深圳市南山区)(无答案) |  | |
| 格式 | rar | ||
| 文件大小 | 39.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-08 17:37:00 | ||
图片预览

文档简介
集训专题:与圆有关的计算(一)
一、关于弦长的计算。
在圆中,关于弦长、弦心距的计算,通常是利用垂径定理构造出由半径、弦心距以及半弦组成的直角三角形,再根据勾股定理,直角三角形中的边角关系来求未知量。
1.已知⊙O的直径AB与弦CD相交于点E,且BC=BD,AE=8,EB=2,则弦CD的长为 。
2.四边形ABCD是⊙O的内接梯形,AB∥CD,⊙O的半径为5cm,AB=6cm,CD=8cm,则梯形的高为 。
3.在以O为圆心,半径分别为5cm和8cm的两个圆中有点Q,OQ=4cm。过点Q分别作大圆的弦AB,小圆的弦EF,则AB的最大值与EF的最小值的和为 。
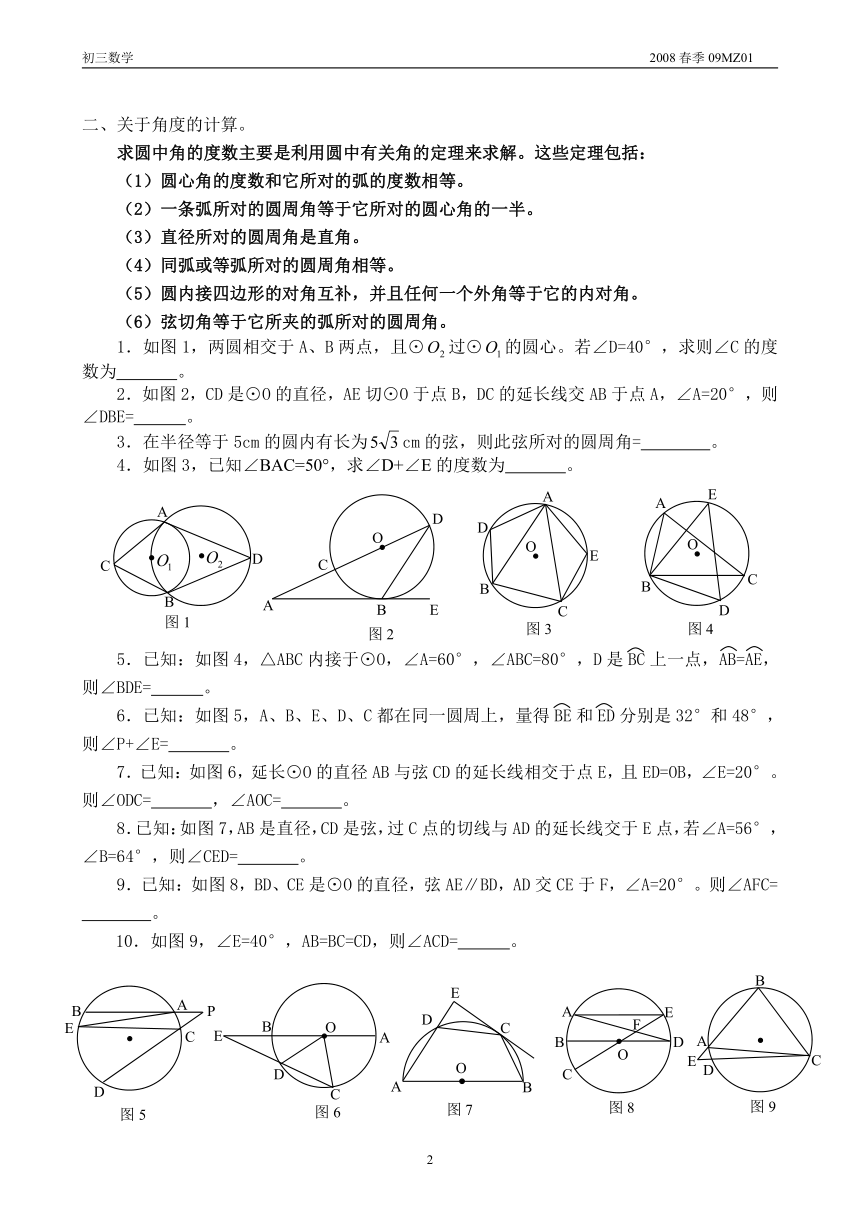
4.如图1,⊙O的直径AB和弦CD相交于点E,已知AE=7cm,EB=3cm,∠BED=30°,则CD的长为 。
5.如图2,⊙O的直径AB=10cm,C是⊙O上一点,点D平分BC,OD交BC于E,DE=2cm,则弦AC= 。
6.如图3,已知△ABC中,∠ACB=90°,AC=6cm,BC=8cm,以C为圆心,CA为半径作圆交斜边AB于D,则AD的长为 。
7.如图4,一弓形弦AB的长为,弓形所在圆的半径为7cm,HG为⊙O的直径,求弓形的高为 。
8.如图5,已知AB是⊙O的直径,过A、B分别作弦EF的垂线交直线EF于C、D,AC=2cm,BD=4cm,⊙O的半径为5cm,则EF的长为 。
9.如图6,已知⊙O是△ABC的外接圆,∠ABC的平分线交⊙O于D,交AC于E,AB=7,AE=3,DE=1,则AD的长为 。
10.如图7,已知AB、CD是⊙O内两条互相垂直的弦,它们相交于圆内一点P,圆的半径是5,两条弦长均为8,则OP的长为 。
二、关于角度的计算。
求圆中角的度数主要是利用圆中有关角的定理来求解。这些定理包括:
(1)圆心角的度数和它所对的弧的度数相等。
(2)一条弧所对的圆周角等于它所对的圆心角的一半。
(3)直径所对的圆周角是直角。
(4)同弧或等弧所对的圆周角相等。
(5)圆内接四边形的对角互补,并且任何一个外角等于它的内对角。
(6)弦切角等于它所夹的弧所对的圆周角。
1.如图1,两圆相交于A、B两点,且⊙过⊙的圆心。若∠D=40°,求则∠C的度数为 。
2.如图2,CD是⊙O的直径,AE切⊙O于点B,DC的延长线交AB于点A,∠A=20°,则∠DBE= 。
3.在半径等于5cm的圆内有长为cm的弦,则此弦所对的圆周角= 。
4.如图3,已知∠BAC=50°,求∠D+∠E的度数为 。
5.已知:如图4,△ABC内接于⊙O,∠A=60°,∠ABC=80°,D是BC上一点,AB=AE,则∠BDE= 。
6.已知:如图5,A、B、E、D、C都在同一圆周上,量得BE和ED分别是32°和48°,则∠P+∠E= 。
7.已知:如图6,延长⊙O的直径AB与弦CD的延长线相交于点E,且ED=OB,∠E=20°。则∠ODC= ,∠AOC= 。
8.已知:如图7,AB是直径,CD是弦,过C点的切线与AD的延长线交于E点,若∠A=56°,∠B=64°,则∠CED= 。
9.已知:如图8,BD、CE是⊙O的直径,弦AE∥BD,AD交CE于F,∠A=20°。则∠AFC=
。
10.如图9,∠E=40°,AB=BC=CD,则∠ACD= 。
三、半径的求法。
圆半径是圆内的特殊线段,其计算的主要方法包括:勾股定理、相交弦定理、切割线定理、利用相似三角形的对应边成比例等等。
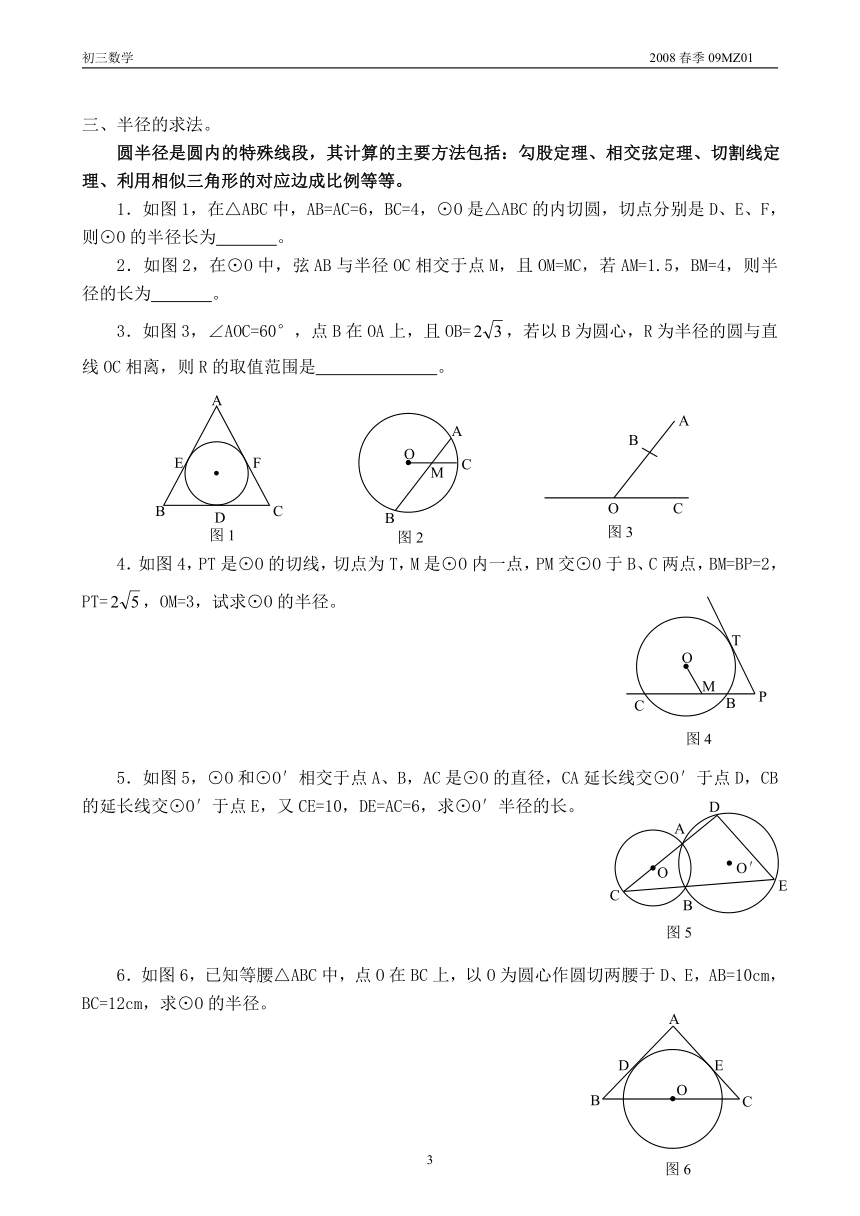
1.如图1,在△ABC中,AB=AC=6,BC=4,⊙O是△ABC的内切圆,切点分别是D、E、F,则⊙O的半径长为 。
2.如图2,在⊙O中,弦AB与半径OC相交于点M,且OM=MC,若AM=1.5,BM=4,则半径的长为 。
3.如图3,∠AOC=60°,点B在OA上,且OB=,若以B为圆心,R为半径的圆与直线OC相离,则R的取值范围是 。
4.如图4,PT是⊙O的切线,切点为T,M是⊙O内一点,PM交⊙O于B、C两点,BM=BP=2,PT=,OM=3,试求⊙O的半径。
5.如图5,⊙O和⊙O′相交于点A、B,AC是⊙O的直径,CA延长线交⊙O′于点D,CB的延长线交⊙O′于点E,又CE=10,DE=AC=6,求⊙O′半径的长。
6.如图6,已知等腰△ABC中,点O在BC上,以O为圆心作圆切两腰于D、E,AB=10cm,BC=12cm,求⊙O的半径。
7.如图7,PA为⊙O的切线,A为切点,PBC是过圆心O的割线。已知PA=10,PB=5,求:(1)⊙O的半径;(2)的值。
8.如图8,已知⊙与⊙相交于C、D两点,连心线和⊙相交于B、A两点,AC、AD的延长线分别和⊙相交于点E、F。(1)求证:CE=DF。(2)如果⊙的半径为2,∠ABC=60°,且EC=CD,求⊙的半径。
9.已知:如图9,△ABC中,∠C=90°,AC=3,BC=4,⊙O、⊙O′分别是△ABC的外接圆、内切圆,⊙O′切AB、BC、CA于D、E、F。求OO′的长。
10.已知:如图10,⊙O的直径AB=4cm,半径OC⊥AB,OC为⊙的直径,⊙与⊙O内切,与⊙外切,且与OA相切,求⊙的半径。
【本课小结】认真思考并解决以下问题,会有意想不到的收获。
1.看到弦,则作 。
2.看到直径,则作 。
3.求弦所对的圆周角,注意 。
4.看到同弧或等弧,注意 。
5.看到切线,则 。
6.看到弦切角,注意 。
7.看到两圆相交,则作 。
8.看到没有给出图形的几何题,小心 。
【作业】日期 姓名 完成时间 成绩
1.如图1,AB是半圆的直径,AC=AD,OC=2,∠CAB=30°,则点O到CD的距离OE= 。
2.已知△ABC内接于⊙O,点D是CA延长线上一点,若∠BOC=120°,则∠BAD= 。
3.如图2,在⊙O中,AB=AC=CD,AB=3,,到EC的长为 。
4.如图3,ABCD是⊙O的内接正方形,AB=4,F是BC的中点,AF的延长线交⊙O于点E,则AE的长为 。
5.△ABC是半径为2cm的圆内接三角形,若BC=cm,则∠A的度数为 。
6.圆内接四边形ABCD中,若∠A: ∠B: ∠C=1:2:3,则∠D的度数为 。
7.A是半径为5的⊙O内一点,且OA=3,过点A且长小于8的弦有 条。
8.如图4,AB、BC是⊙O的两条弦,且AB⊥BC,又BE=AE,CF=BC,若⊙O半径为5cm,那么EF= cm。
9.如图5,已知半圆的圆心在Rt△ABC的斜边上,且半圆分别切AB、AC于D、E,AB=3cm,AC=4cm,则半圆的半径是 。
10.如图6,PC切⊙O于C,PO交⊙O于A,DA切⊙O于A交PC于D,若1:3,AD=2,则⊙O的半径为 。
11.如图7,点O为⊙O′上任意一点,⊙O与⊙O′相交于A、B,E是优弧AB上的一点,EO交⊙O于C、D,交AB于F,且CF=1,EC=2,则⊙O的半径是 。
12.如图8,点P是⊙O的直径AB延长线上一点,PT切⊙O于点T,已知PT=4,PB=2,⊙O的半径是 。
一、关于弦长的计算。
在圆中,关于弦长、弦心距的计算,通常是利用垂径定理构造出由半径、弦心距以及半弦组成的直角三角形,再根据勾股定理,直角三角形中的边角关系来求未知量。
1.已知⊙O的直径AB与弦CD相交于点E,且BC=BD,AE=8,EB=2,则弦CD的长为 。
2.四边形ABCD是⊙O的内接梯形,AB∥CD,⊙O的半径为5cm,AB=6cm,CD=8cm,则梯形的高为 。
3.在以O为圆心,半径分别为5cm和8cm的两个圆中有点Q,OQ=4cm。过点Q分别作大圆的弦AB,小圆的弦EF,则AB的最大值与EF的最小值的和为 。
4.如图1,⊙O的直径AB和弦CD相交于点E,已知AE=7cm,EB=3cm,∠BED=30°,则CD的长为 。
5.如图2,⊙O的直径AB=10cm,C是⊙O上一点,点D平分BC,OD交BC于E,DE=2cm,则弦AC= 。
6.如图3,已知△ABC中,∠ACB=90°,AC=6cm,BC=8cm,以C为圆心,CA为半径作圆交斜边AB于D,则AD的长为 。
7.如图4,一弓形弦AB的长为,弓形所在圆的半径为7cm,HG为⊙O的直径,求弓形的高为 。
8.如图5,已知AB是⊙O的直径,过A、B分别作弦EF的垂线交直线EF于C、D,AC=2cm,BD=4cm,⊙O的半径为5cm,则EF的长为 。
9.如图6,已知⊙O是△ABC的外接圆,∠ABC的平分线交⊙O于D,交AC于E,AB=7,AE=3,DE=1,则AD的长为 。
10.如图7,已知AB、CD是⊙O内两条互相垂直的弦,它们相交于圆内一点P,圆的半径是5,两条弦长均为8,则OP的长为 。
二、关于角度的计算。
求圆中角的度数主要是利用圆中有关角的定理来求解。这些定理包括:
(1)圆心角的度数和它所对的弧的度数相等。
(2)一条弧所对的圆周角等于它所对的圆心角的一半。
(3)直径所对的圆周角是直角。
(4)同弧或等弧所对的圆周角相等。
(5)圆内接四边形的对角互补,并且任何一个外角等于它的内对角。
(6)弦切角等于它所夹的弧所对的圆周角。
1.如图1,两圆相交于A、B两点,且⊙过⊙的圆心。若∠D=40°,求则∠C的度数为 。
2.如图2,CD是⊙O的直径,AE切⊙O于点B,DC的延长线交AB于点A,∠A=20°,则∠DBE= 。
3.在半径等于5cm的圆内有长为cm的弦,则此弦所对的圆周角= 。
4.如图3,已知∠BAC=50°,求∠D+∠E的度数为 。
5.已知:如图4,△ABC内接于⊙O,∠A=60°,∠ABC=80°,D是BC上一点,AB=AE,则∠BDE= 。
6.已知:如图5,A、B、E、D、C都在同一圆周上,量得BE和ED分别是32°和48°,则∠P+∠E= 。
7.已知:如图6,延长⊙O的直径AB与弦CD的延长线相交于点E,且ED=OB,∠E=20°。则∠ODC= ,∠AOC= 。
8.已知:如图7,AB是直径,CD是弦,过C点的切线与AD的延长线交于E点,若∠A=56°,∠B=64°,则∠CED= 。
9.已知:如图8,BD、CE是⊙O的直径,弦AE∥BD,AD交CE于F,∠A=20°。则∠AFC=
。
10.如图9,∠E=40°,AB=BC=CD,则∠ACD= 。
三、半径的求法。
圆半径是圆内的特殊线段,其计算的主要方法包括:勾股定理、相交弦定理、切割线定理、利用相似三角形的对应边成比例等等。
1.如图1,在△ABC中,AB=AC=6,BC=4,⊙O是△ABC的内切圆,切点分别是D、E、F,则⊙O的半径长为 。
2.如图2,在⊙O中,弦AB与半径OC相交于点M,且OM=MC,若AM=1.5,BM=4,则半径的长为 。
3.如图3,∠AOC=60°,点B在OA上,且OB=,若以B为圆心,R为半径的圆与直线OC相离,则R的取值范围是 。
4.如图4,PT是⊙O的切线,切点为T,M是⊙O内一点,PM交⊙O于B、C两点,BM=BP=2,PT=,OM=3,试求⊙O的半径。
5.如图5,⊙O和⊙O′相交于点A、B,AC是⊙O的直径,CA延长线交⊙O′于点D,CB的延长线交⊙O′于点E,又CE=10,DE=AC=6,求⊙O′半径的长。
6.如图6,已知等腰△ABC中,点O在BC上,以O为圆心作圆切两腰于D、E,AB=10cm,BC=12cm,求⊙O的半径。
7.如图7,PA为⊙O的切线,A为切点,PBC是过圆心O的割线。已知PA=10,PB=5,求:(1)⊙O的半径;(2)的值。
8.如图8,已知⊙与⊙相交于C、D两点,连心线和⊙相交于B、A两点,AC、AD的延长线分别和⊙相交于点E、F。(1)求证:CE=DF。(2)如果⊙的半径为2,∠ABC=60°,且EC=CD,求⊙的半径。
9.已知:如图9,△ABC中,∠C=90°,AC=3,BC=4,⊙O、⊙O′分别是△ABC的外接圆、内切圆,⊙O′切AB、BC、CA于D、E、F。求OO′的长。
10.已知:如图10,⊙O的直径AB=4cm,半径OC⊥AB,OC为⊙的直径,⊙与⊙O内切,与⊙外切,且与OA相切,求⊙的半径。
【本课小结】认真思考并解决以下问题,会有意想不到的收获。
1.看到弦,则作 。
2.看到直径,则作 。
3.求弦所对的圆周角,注意 。
4.看到同弧或等弧,注意 。
5.看到切线,则 。
6.看到弦切角,注意 。
7.看到两圆相交,则作 。
8.看到没有给出图形的几何题,小心 。
【作业】日期 姓名 完成时间 成绩
1.如图1,AB是半圆的直径,AC=AD,OC=2,∠CAB=30°,则点O到CD的距离OE= 。
2.已知△ABC内接于⊙O,点D是CA延长线上一点,若∠BOC=120°,则∠BAD= 。
3.如图2,在⊙O中,AB=AC=CD,AB=3,,到EC的长为 。
4.如图3,ABCD是⊙O的内接正方形,AB=4,F是BC的中点,AF的延长线交⊙O于点E,则AE的长为 。
5.△ABC是半径为2cm的圆内接三角形,若BC=cm,则∠A的度数为 。
6.圆内接四边形ABCD中,若∠A: ∠B: ∠C=1:2:3,则∠D的度数为 。
7.A是半径为5的⊙O内一点,且OA=3,过点A且长小于8的弦有 条。
8.如图4,AB、BC是⊙O的两条弦,且AB⊥BC,又BE=AE,CF=BC,若⊙O半径为5cm,那么EF= cm。
9.如图5,已知半圆的圆心在Rt△ABC的斜边上,且半圆分别切AB、AC于D、E,AB=3cm,AC=4cm,则半圆的半径是 。
10.如图6,PC切⊙O于C,PO交⊙O于A,DA切⊙O于A交PC于D,若1:3,AD=2,则⊙O的半径为 。
11.如图7,点O为⊙O′上任意一点,⊙O与⊙O′相交于A、B,E是优弧AB上的一点,EO交⊙O于C、D,交AB于F,且CF=1,EC=2,则⊙O的半径是 。
12.如图8,点P是⊙O的直径AB延长线上一点,PT切⊙O于点T,已知PT=4,PB=2,⊙O的半径是 。
