2024北师版九年级数学下学期期末综合测试卷(含答案)
文档属性
| 名称 | 2024北师版九年级数学下学期期末综合测试卷(含答案) | 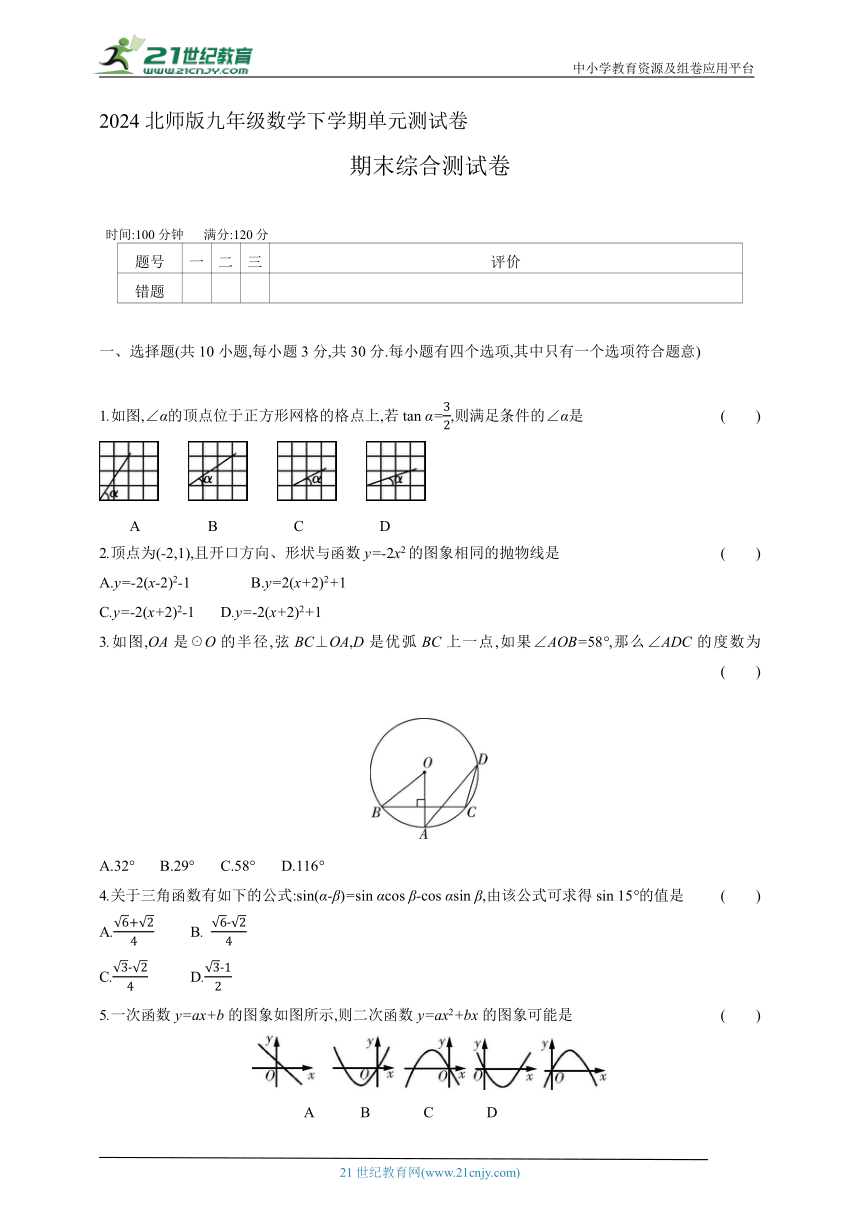 | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 16:11:47 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024北师版九年级数学下学期单元测试卷
期末综合测试卷
时间:100分钟 满分:120分
题号 一 二 三 评价
错题
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.如图,∠α的顶点位于正方形网格的格点上,若tan α=,则满足条件的∠α是 ( )
A B C D
2.顶点为(-2,1),且开口方向、形状与函数y=-2x2的图象相同的抛物线是 ( )
A.y=-2(x-2)2-1 B.y=2(x+2)2+1
C.y=-2(x+2)2-1 D.y=-2(x+2)2+1
3.如图,OA是☉O的半径,弦BC⊥OA,D是优弧BC上一点,如果∠AOB=58°,那么∠ADC的度数为 ( )
A.32° B.29° C.58° D.116°
4.关于三角函数有如下的公式:sin(α-β)=sin αcos β-cos αsin β,由该公式可求得sin 15°的值是 ( )
A. B.
C. D.
5.一次函数y=ax+b的图象如图所示,则二次函数y=ax2+bx的图象可能是 ( )
A B C D
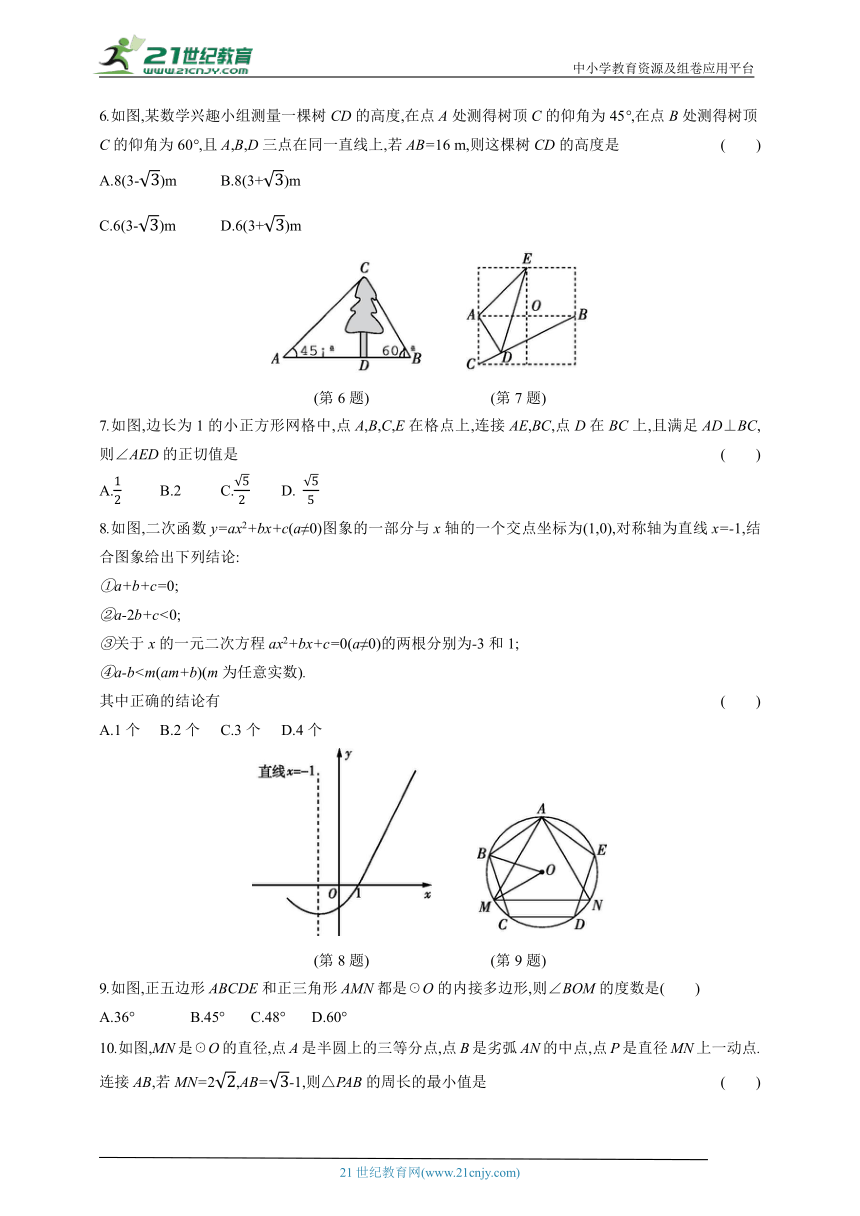
6.如图,某数学兴趣小组测量一棵树CD的高度,在点A处测得树顶C的仰角为45°,在点B处测得树顶C的仰角为60°,且A,B,D三点在同一直线上,若AB=16 m,则这棵树CD的高度是 ( )
A.8(3-)m B.8(3+)m
C.6(3-)m D.6(3+)m
(第6题) (第7题)
7.如图,边长为1的小正方形网格中,点A,B,C,E在格点上,连接AE,BC,点D在BC上,且满足AD⊥BC,则∠AED的正切值是 ( )
A. B.2 C. D.
8.如图,二次函数y=ax2+bx+c(a≠0)图象的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=-1,结合图象给出下列结论:
①a+b+c=0;
②a-2b+c<0;
③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为-3和1;
④a-b其中正确的结论有 ( )
A.1个 B.2个 C.3个 D.4个
(第8题) (第9题)
9.如图,正五边形ABCDE和正三角形AMN都是☉O的内接多边形,则∠BOM的度数是( )
A.36° B.45° C.48° D.60°
10.如图,MN是☉O的直径,点A是半圆上的三等分点,点B是劣弧AN的中点,点P是直径MN上一动点.连接AB,若MN=2,AB=-1,则△PAB的周长的最小值是 ( )
A.2+1 B.+1
C.2 D.+1
二、填空题(共5小题,每小题3分,共15分)
11.已知点A(x1,y1),B(x2,y2)在二次函数y=(x-3)2+2的图象上,若x1”“<”或“=”).
12.如图,河堤横断面迎水坡AB的坡度i=1∶,堤高BC=10米,则坡面AB的长度是 米.
(第12题) (第13题)
13.往水平放置的半径为13 cm的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度AB=24 cm,则水的最大深度为 cm.
14.如图,在△ABC中,∠ACB=90°,AC=BC=2,将△ABC绕AC的中点D逆时针旋转90°得到△A'B'C',其中点B的运动路径为,则图中阴影部分的面积为 .
(第14题) (第15题)
15.如图,在平面直角坐标系中,已知点A的坐标为(4,0),O为坐标原点,且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.过点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为F,连接EF,当线段EF的长度最短时,点P的坐标为 .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15.
三、解答题(共8小题,共75分)
16.(7分)已知二次函数y=x2+bx-3的图象经过点P(-2,5).
(1)求b的值;
(2)设P1(4,y1),P2(5,y2),P3(6,y3)均在该函数图象上,y1,y2,y3能否作为同一个三角形三边的长 请说明理由.
17.(7分)小龙同学在学习三角函数知识时,老师告诉他求一个角的三角函数值,这个角应该在直角三角形环境里才好求,但是小龙在解题过程中遇到了这样一个难题,题目:在Rt△ABC中,∠C=90°,若∠BDC=60°,AD=2BD,求sin∠ABD的值.
你能运用所学知识帮他解决吗
18.(8分)如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与☉O的位置关系,并说明理由;
(2)若BD=2,BF=2,求☉O的半径.
19.(8分)掷实心球是兰州市高中阶段学校招生体育考试的选考项目.如图(1)是一名女生投实心球,实心球行进路线是一条抛物线,行进高度y(m)与水平距离x(m)之间的函数关系如图(2)所示,掷出时起点处高度为 m,当水平距离为3 m时,实心球行进至最高点3 m处.
(1)求y关于x的函数表达式;
(2)根据兰州市高中阶段学校招生体育考试评分标准(女生),投掷过程中,实心球从起点到落地点的水平距离大于等于6.70 m,此项考试得分为满分10分.该女生在此项考试中是否得满分,请说明理由.
图(1) 图(2)
图(1)来源:《2022年兰州市高中阶段学校招生体育考试规则与测试要求》
20.(10分)圭表[如图(1)]是我国古代一种通过测量正午日影长度来推定节气的天文仪器,它包括一根直立的标杆(称为“表”)和一把呈南北方向水平固定摆放的与标杆垂直的长尺(称为“圭”),当正午太阳照射在表上时,日影便会投影在圭面上,圭面上日影长度最长的那一天定为冬至,日影长度最短的那一天定为夏至.图(2)是一个根据某市地理位置设计的圭表平面示意图,表AC垂直圭BC,已知该市冬至正午太阳高度角(即∠ABC)为37°,夏至正午太阳高度角(即∠ADC)为84°,圭面上冬至线与夏至线之间的距离(即DB的长)为4米.
图(1) 图(2)
(1)求∠BAD的度数;
(2)求表AC的长(最后结果精确到0.1米).
(参考数据:sin 37°≈,cos 37°≈,tan 37°≈,tan 84°≈)
21.(11分)如图,线段AB为☉O的弦,点D,C为的三等分点,AC∥BE.
(1)求证:∠A=∠E;
(2)若BC=3,BE=5,求CE的长.
22.(11分)如图,抛物线y=x2+bx+c(b,c是常数)的顶点为C,与x轴交于A,B两点,A(1,0),AB=4,点P为线段AB上的动点,过P作PQ∥BC交AC于点Q.
(1)求该抛物线的解析式;
(2)求△CPQ面积的最大值,并求此时P点坐标.
23.(13分)一个玻璃球体近似半圆O,AB为直径.半圆O上点C处有个吊灯EF,EF∥AB,CO⊥AB,EF的中点为D,OA=4.
(1)如图(1),CM为一条拉线,M在OB上,OM=1.6,DF=0.8,求CD的长度;
(2)如图(2),一个玻璃镜与圆O相切,H为切点,M为OB上一点,MH为入射光线,NH为反射光线,∠OHM=∠OHN=45°,tan∠COH=,求ON的长度;
(3)如图(3),M是线段OB上的动点,MH为入射光线,∠HOM=50°,HN为反射光线交圆O于点N,在M从O运动到B的过程中,求N点的运动路径长.
九年级下册期末综合测试卷
选择填空题答案速查
1 2 3 4 5 6 7 8 9 10
A D B B D A A C C B
11.> 12.20 13.8
14.- 15.(,2)或(,2)
1.A
2.D 根据题意,得y=-2(x+2)2+1.故选D.
3.B ∵BC⊥OA,∴=,∴∠ADC=∠AOB=×58°=29°.故选B.
4.B sin 15°=sin(45°-30°)=sin 45°cos 30°-cos 45°sin 30°=
×-×=.故选B.
一题多解
sin 15°=sin(60°-45°)=sin 60°cos 45°-cos 60°sin 45°=×-×=.
5.D 由题图可知,一次函数y=ax+b的图象经过第一、二、四象限,∴a<0,b>0,∴二次函数y=ax2+bx的图象开口方向向下.∵->0,∴对称轴在y轴右侧.故选D.
6.A 设AD=x m,∵AB=16 m,∴BD=AB-AD=(16-x)(m).在Rt△ADC中,∠A=45°,
∴CD=AD·tan 45°=x(m).在Rt△CDB中,∠B=60°,∴tan 60°===,
∴x=24-8,经检验,x=24-8是原方程的根,∴CD=24-8=8(3-)(m),∴这棵树CD的高度是8(3-)m.故选A.
7.A
图示速解
如图,连接OD,∵AD⊥BC,O是AB中点,∴OD=AB=1,∴OD=OA=OE=OD,∴点A,D,B,E在以O为圆心,1为半径的同一个圆上,∴∠ABC=∠AED,∴tan∠AED=tan∠ABD==.故选A.
8.C ∵二次函数y=ax2+bx+c(a≠0)图象的一部分与x轴的一个交点坐标为(1,0),∴a+b+c=0,故①正确.∵抛物线的对称轴为直线x=-=-1,∴b=2a>0.∵抛物线开口向上,与y轴交于负半轴,∴a>0,c<0,∴a-2b+c=c-3a<0,故②正确.由题意,得抛物线与x轴的另一交点为(-3,0),∴关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为-3和1,故③正确.∵x=-1时,y有最小值,∴a-b+c≤am2+bm+c(m为任意实数),∴a-b≤m(am+b),故④不正确.综上,正确的结论有①②③,共3个.故选C.
9.C 如图,连接AO.∵△AMN是等边三角形,∴∠ANM=60°,∴∠AOM=2∠ANM=
120°.∵五边形ABCDE是正五边形,∴∠AOB==72°,∴∠BOM=120°-72°=
48°.故选C.
10.B 如图,作点A关于MN的对称点A',连接A'B,交MN于点P,连接AA',OA',OA,OB,PA.∵点A与点A'关于MN对称,∴PA=PA'.∵点A是半圆上的三等分点,∴∠A'ON=∠AON=60°.∵点B是劣弧AN的中点,∴∠BON=30°,∴∠A'OB=
∠A'ON+∠BON=90°.又∵OB=OA'=,∴A'B=2,∴PA+PB=PA'+PB=A'B=2.
∵AB=-1,∴△PAB的周长的最小值是2+-1=+1.故选B.
高分锦囊
将军饮马模型
如图,在直线l同侧有两个定点A,B,在直线l上求作点P,使得PA+PB的值最小. 如图,作点A关于直线l的对称点A',连接A'B,A'B与直线l的交点即为点P.
如图,在直线l同侧有两个定点A,B,在直线l上求作点P,使得|PA-PB|的值最大. 如图,连接BA并延长,BA的延长线与直线l的交点即为点P.
如图,在直线l两侧各有一个定点A,B,在直线l上求作点P,使得|PA-PB|的值最大. 如图,作点B关于直线l的对称点B',连接AB'并延长,AB'的延长线与直线l的交点即为点P.
如图,在直线l同侧有两个定点A,B,在直线l上求作点P,使得|PA-PB|的值最小. 如图,连接AB,作线段AB的垂直平分线,该线与直线l的交点即为点P,此时|PA-PB|=0.
11.> ∵y=(x-3)2+2,∴抛物线的对称轴为直线x=3,抛物线开口向上.∵点A(x1,y1),B(x2,y2)在二次函数y=(x-3)2+2的图象上,且x1y2.
快解妙解
∵x1, ∴y1>y2.
12.20 ∵迎水坡AB的坡度i=1∶,∴=,∴AC=BC=10(米),在Rt△ABC中,由勾股定理,得AB===20(米).
13.8 如图,连接OB,过点O作OC⊥AB于点D,交☉O于点C.∵AB=24 cm,∴BD=AB=12 cm.∵OB=OC=13 cm,∴在Rt△OBD中,OD===5(cm),
∴CD=OC-OD=13-5=8(cm).
14.- 如图,连接B'D,BD,由题意可得BC=B'C',AC=A'C',∠BDB'=90°.∵D为AC的中点,∴C'D=CD=AC=1.在Rt△BCD中,由勾股定理,得BD==
=,∴S扇形BDB'==.又易知S△DCB'+S△BCD=S梯形CDC'B'=C'D×(CD+C'B')=
×1×3=,∴S阴影=S扇形BDB'-(S△DCB'+S△BCD)=-.
15.(,2)或(,2) 连接OD(图略),由题意可知,四边形OFDE是矩形,∴OD=EF.根据垂线段最短,可得当OD⊥AC时,OD最短,此时EF最短.在Rt△AOC中,∵OC=OA=4,∴当D是AC的中点时,OD⊥AC.∵DF∥OC,∴DF=OC=2,∴点P的纵坐标是2.∵点A的坐标为(4,0),且OA=OC=4OB,∴点B的坐标为(-1,0),点C的坐标为(0,4).设过A,B,C三点的抛物线的函数解析式为y=ax2+bx+4,把A,B的坐标分别代入可得a=-1,b=3,∴抛物线的函数解析式为 y=-x2+3x+4.当y=2时,x2-3x-2=0,解得x=.∴当线段EF的长度最短时,点P的坐标为(,2)或(,2).
16.【参考答案】(1)把(-2,5)代入二次函数y=x2+bx-3,
得5=4-2b-3,
∴b=-2. (3分)
(2)y1,y2,y3不能作为同一个三角形三边的长.
理由:把P1(4,y1),P2(5,y2),P3(6,y3)的坐标代入y=x2-2x-3,得y1=5,y2=12,y3=21.
∵5+12<21,
∴y1,y2,y3不能作为同一个三角形三边的长. (7分)
17.【参考答案】 如图,过A点作AE⊥BD交BD的延长线于E点.
∴∠AED=∠C=90°.
在Rt△BDC中,∠BDC=60°,
∴cos∠BDC==. (2分)
设CD=a,则BD=2a.
在Rt△BDC中,由勾股定理,得BC=a.
∵AD=2BD,
∴AD=4a,
∴AC=5a. (4分)
在Rt△ACB中,由勾股定理,得AB=2a.
在Rt△ADE中,sin∠ADE==,
∴AE=2a. (6分)
在Rt△ABE中,sin∠ABD==. (7分)
18.【解题思路】(1)连接OD,先得出OD∥AC,然后由∠C=90°得出OD⊥BC即可;(2)设☉O的半径为r,根据勾股定理列方程,求解即可.
【参考答案】(1)相切. (1分)
理由:如图,连接OD, ∵OA=OD,
∴∠OAD=∠ODA.
∵AD平分∠CAB,
∴∠OAD=∠CAD,
∴∠ODA=∠CAD,
∴OD∥AC.
∵∠C=90°,
∴∠ODB=90°,即OD⊥BC.
∵OD为☉O的半径,
∴直线BC与☉O的位置关系是相切. (4分)
(2)设☉O的半径为r,则OD=OF=r. (5分)
在Rt△BDO中,由勾股定理,得OB2=BD2+OD2,
即(r+2)2=(2)2+r2,解得r=2.
即☉O的半径是2. (8分)
19.【参考答案】 (1)根据题意设y关于x的函数表达式为y=a(x-3)2+3,
把(0,)代入表达式,得=a(0-3)2+3,
解得a=-,
∴y关于x的函数表达式为y=-(x-3)2+3. (4分)
(2)该女生在此项考试中是得满分,
理由:令y=0,则-(x-3)2+3=0,
解得x1=7.5,x2=-1.5(舍去).
∵7.5>6.70,
∴该女生在此项考试中是得满分. (8分)
20.【参考答案】 (1)∵∠ADC=84°,∠ABC=37°,
∴∠BAD=∠ADC-∠ABC=47°. (3分)
(2)在Rt△ABC中,tan∠ABC=tan 37°=,
∴BC=.
同理,在Rt△ADC中,DC=.
∵BD=4米,
∴BC-DC=-=BD=4米,
∴AC-AC≈4米,
∴AC≈3.3米.
答:表AC的长约是3.3米. (10分)
21.【参考答案】(1)证明:∵AC∥BE,
∴∠E=∠ACD.
∵点D,C为的三等分点,
∴==,
∴∠A=∠ACD,
∴∠E=∠A. (5分)
(2)由(1)知==,
∴∠D=∠CBD=∠A=∠E,
∴BE=BD=5,BC=CD=3,△CBD∽△BDE,
∴=,即=,
解得DE=,
∴CE=DE-CD=-3=. (11分)
22.【参考答案】 (1)∵A(1,0),AB=4,
∴B(-3,0).
将A(1,0),B(-3,0)分别代入y=x2+bx+c,
得解得
故抛物线的解析式为y=x2+2x-3. (5分)
(2)∵y=x2+2x-3=(x+1)2-4,
∴C(-1,-4).
设P(m,0),则AP=1-m.
由PQ∥BC,易得△APQ∽△ABC,
∴=()2=()2=.
又S△ABC=×4×4=8,
∴S△APQ=8×=,
∴S△CPQ=S△APC-S△APQ=×(1-m)×4-=-(m+1)2+2. (9分)
∵-<0,
∴当m=-1时,S△CPQ最大,最大值为2, (10分)
此时点P的坐标为(-1,0). (11分)
23.【解题思路】 (1)根据三角形相似可知,即点D是OC的中点,进而得到DC=OC;(2)过点N作ND⊥OH于点D,说明△NHD是等腰直角三角形,得ND=HD,借助tan∠COH=表示出ND,OD,再根据勾股定理求解;(3)当点M与点O重合时,点N也与点O重合,当点M运动至点B时,点N运动至点T,故点N的运动路径长为OA+的长.
【参考答案】 (1)∵OM=1.6,DF=0.8,EF∥AB,
∴△CDF∽△COM,
∴=.
∵OM=1.6,DF=0.8,
∴==,
∴CD=OC.
∵OC=OA=4,
∴CD=2. (4分)
(2)如图,过点N作ND⊥OH于点D.
∵∠OHN=45°,
∴△NHD是等腰直角三角形,
∴ND=HD.
∵tan∠COH=,∠NDO=90°,
∴=.
设ND=3x=HD,则OD=4x.
∵OH=OA=4,
∴OH=3x+4x=4,
∴x=,
∴ND=×3=,OD=×4=,
∴ON==. (8分)
(3)如图,当点M与点O重合时,点N也与点O重合,当点M运动至点B时,点N运动至点T,故点N的运动路径长为OA+的长.
∵∠HOM=50°,OH=OB,
∴∠OHB=∠OBH=65°.
∵∠OHM=∠OHT,OH=OT,
∴∠OTH=∠OHT=65°,
∴∠TOH=50°,
∴∠AOT=180°-50°-50°=80°,
∴的长==π,
∴点N的运动路径长=4+π. (13分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师版九年级数学下学期单元测试卷
期末综合测试卷
时间:100分钟 满分:120分
题号 一 二 三 评价
错题
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.如图,∠α的顶点位于正方形网格的格点上,若tan α=,则满足条件的∠α是 ( )
A B C D
2.顶点为(-2,1),且开口方向、形状与函数y=-2x2的图象相同的抛物线是 ( )
A.y=-2(x-2)2-1 B.y=2(x+2)2+1
C.y=-2(x+2)2-1 D.y=-2(x+2)2+1
3.如图,OA是☉O的半径,弦BC⊥OA,D是优弧BC上一点,如果∠AOB=58°,那么∠ADC的度数为 ( )
A.32° B.29° C.58° D.116°
4.关于三角函数有如下的公式:sin(α-β)=sin αcos β-cos αsin β,由该公式可求得sin 15°的值是 ( )
A. B.
C. D.
5.一次函数y=ax+b的图象如图所示,则二次函数y=ax2+bx的图象可能是 ( )
A B C D
6.如图,某数学兴趣小组测量一棵树CD的高度,在点A处测得树顶C的仰角为45°,在点B处测得树顶C的仰角为60°,且A,B,D三点在同一直线上,若AB=16 m,则这棵树CD的高度是 ( )
A.8(3-)m B.8(3+)m
C.6(3-)m D.6(3+)m
(第6题) (第7题)
7.如图,边长为1的小正方形网格中,点A,B,C,E在格点上,连接AE,BC,点D在BC上,且满足AD⊥BC,则∠AED的正切值是 ( )
A. B.2 C. D.
8.如图,二次函数y=ax2+bx+c(a≠0)图象的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=-1,结合图象给出下列结论:
①a+b+c=0;
②a-2b+c<0;
③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为-3和1;
④a-b
A.1个 B.2个 C.3个 D.4个
(第8题) (第9题)
9.如图,正五边形ABCDE和正三角形AMN都是☉O的内接多边形,则∠BOM的度数是( )
A.36° B.45° C.48° D.60°
10.如图,MN是☉O的直径,点A是半圆上的三等分点,点B是劣弧AN的中点,点P是直径MN上一动点.连接AB,若MN=2,AB=-1,则△PAB的周长的最小值是 ( )
A.2+1 B.+1
C.2 D.+1
二、填空题(共5小题,每小题3分,共15分)
11.已知点A(x1,y1),B(x2,y2)在二次函数y=(x-3)2+2的图象上,若x1
12.如图,河堤横断面迎水坡AB的坡度i=1∶,堤高BC=10米,则坡面AB的长度是 米.
(第12题) (第13题)
13.往水平放置的半径为13 cm的圆柱形容器内装入一些水以后,截面图如图所示,若水面宽度AB=24 cm,则水的最大深度为 cm.
14.如图,在△ABC中,∠ACB=90°,AC=BC=2,将△ABC绕AC的中点D逆时针旋转90°得到△A'B'C',其中点B的运动路径为,则图中阴影部分的面积为 .
(第14题) (第15题)
15.如图,在平面直角坐标系中,已知点A的坐标为(4,0),O为坐标原点,且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.过点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为F,连接EF,当线段EF的长度最短时,点P的坐标为 .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15.
三、解答题(共8小题,共75分)
16.(7分)已知二次函数y=x2+bx-3的图象经过点P(-2,5).
(1)求b的值;
(2)设P1(4,y1),P2(5,y2),P3(6,y3)均在该函数图象上,y1,y2,y3能否作为同一个三角形三边的长 请说明理由.
17.(7分)小龙同学在学习三角函数知识时,老师告诉他求一个角的三角函数值,这个角应该在直角三角形环境里才好求,但是小龙在解题过程中遇到了这样一个难题,题目:在Rt△ABC中,∠C=90°,若∠BDC=60°,AD=2BD,求sin∠ABD的值.
你能运用所学知识帮他解决吗
18.(8分)如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
(1)试判断直线BC与☉O的位置关系,并说明理由;
(2)若BD=2,BF=2,求☉O的半径.
19.(8分)掷实心球是兰州市高中阶段学校招生体育考试的选考项目.如图(1)是一名女生投实心球,实心球行进路线是一条抛物线,行进高度y(m)与水平距离x(m)之间的函数关系如图(2)所示,掷出时起点处高度为 m,当水平距离为3 m时,实心球行进至最高点3 m处.
(1)求y关于x的函数表达式;
(2)根据兰州市高中阶段学校招生体育考试评分标准(女生),投掷过程中,实心球从起点到落地点的水平距离大于等于6.70 m,此项考试得分为满分10分.该女生在此项考试中是否得满分,请说明理由.
图(1) 图(2)
图(1)来源:《2022年兰州市高中阶段学校招生体育考试规则与测试要求》
20.(10分)圭表[如图(1)]是我国古代一种通过测量正午日影长度来推定节气的天文仪器,它包括一根直立的标杆(称为“表”)和一把呈南北方向水平固定摆放的与标杆垂直的长尺(称为“圭”),当正午太阳照射在表上时,日影便会投影在圭面上,圭面上日影长度最长的那一天定为冬至,日影长度最短的那一天定为夏至.图(2)是一个根据某市地理位置设计的圭表平面示意图,表AC垂直圭BC,已知该市冬至正午太阳高度角(即∠ABC)为37°,夏至正午太阳高度角(即∠ADC)为84°,圭面上冬至线与夏至线之间的距离(即DB的长)为4米.
图(1) 图(2)
(1)求∠BAD的度数;
(2)求表AC的长(最后结果精确到0.1米).
(参考数据:sin 37°≈,cos 37°≈,tan 37°≈,tan 84°≈)
21.(11分)如图,线段AB为☉O的弦,点D,C为的三等分点,AC∥BE.
(1)求证:∠A=∠E;
(2)若BC=3,BE=5,求CE的长.
22.(11分)如图,抛物线y=x2+bx+c(b,c是常数)的顶点为C,与x轴交于A,B两点,A(1,0),AB=4,点P为线段AB上的动点,过P作PQ∥BC交AC于点Q.
(1)求该抛物线的解析式;
(2)求△CPQ面积的最大值,并求此时P点坐标.
23.(13分)一个玻璃球体近似半圆O,AB为直径.半圆O上点C处有个吊灯EF,EF∥AB,CO⊥AB,EF的中点为D,OA=4.
(1)如图(1),CM为一条拉线,M在OB上,OM=1.6,DF=0.8,求CD的长度;
(2)如图(2),一个玻璃镜与圆O相切,H为切点,M为OB上一点,MH为入射光线,NH为反射光线,∠OHM=∠OHN=45°,tan∠COH=,求ON的长度;
(3)如图(3),M是线段OB上的动点,MH为入射光线,∠HOM=50°,HN为反射光线交圆O于点N,在M从O运动到B的过程中,求N点的运动路径长.
九年级下册期末综合测试卷
选择填空题答案速查
1 2 3 4 5 6 7 8 9 10
A D B B D A A C C B
11.> 12.20 13.8
14.- 15.(,2)或(,2)
1.A
2.D 根据题意,得y=-2(x+2)2+1.故选D.
3.B ∵BC⊥OA,∴=,∴∠ADC=∠AOB=×58°=29°.故选B.
4.B sin 15°=sin(45°-30°)=sin 45°cos 30°-cos 45°sin 30°=
×-×=.故选B.
一题多解
sin 15°=sin(60°-45°)=sin 60°cos 45°-cos 60°sin 45°=×-×=.
5.D 由题图可知,一次函数y=ax+b的图象经过第一、二、四象限,∴a<0,b>0,∴二次函数y=ax2+bx的图象开口方向向下.∵->0,∴对称轴在y轴右侧.故选D.
6.A 设AD=x m,∵AB=16 m,∴BD=AB-AD=(16-x)(m).在Rt△ADC中,∠A=45°,
∴CD=AD·tan 45°=x(m).在Rt△CDB中,∠B=60°,∴tan 60°===,
∴x=24-8,经检验,x=24-8是原方程的根,∴CD=24-8=8(3-)(m),∴这棵树CD的高度是8(3-)m.故选A.
7.A
图示速解
如图,连接OD,∵AD⊥BC,O是AB中点,∴OD=AB=1,∴OD=OA=OE=OD,∴点A,D,B,E在以O为圆心,1为半径的同一个圆上,∴∠ABC=∠AED,∴tan∠AED=tan∠ABD==.故选A.
8.C ∵二次函数y=ax2+bx+c(a≠0)图象的一部分与x轴的一个交点坐标为(1,0),∴a+b+c=0,故①正确.∵抛物线的对称轴为直线x=-=-1,∴b=2a>0.∵抛物线开口向上,与y轴交于负半轴,∴a>0,c<0,∴a-2b+c=c-3a<0,故②正确.由题意,得抛物线与x轴的另一交点为(-3,0),∴关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为-3和1,故③正确.∵x=-1时,y有最小值,∴a-b+c≤am2+bm+c(m为任意实数),∴a-b≤m(am+b),故④不正确.综上,正确的结论有①②③,共3个.故选C.
9.C 如图,连接AO.∵△AMN是等边三角形,∴∠ANM=60°,∴∠AOM=2∠ANM=
120°.∵五边形ABCDE是正五边形,∴∠AOB==72°,∴∠BOM=120°-72°=
48°.故选C.
10.B 如图,作点A关于MN的对称点A',连接A'B,交MN于点P,连接AA',OA',OA,OB,PA.∵点A与点A'关于MN对称,∴PA=PA'.∵点A是半圆上的三等分点,∴∠A'ON=∠AON=60°.∵点B是劣弧AN的中点,∴∠BON=30°,∴∠A'OB=
∠A'ON+∠BON=90°.又∵OB=OA'=,∴A'B=2,∴PA+PB=PA'+PB=A'B=2.
∵AB=-1,∴△PAB的周长的最小值是2+-1=+1.故选B.
高分锦囊
将军饮马模型
如图,在直线l同侧有两个定点A,B,在直线l上求作点P,使得PA+PB的值最小. 如图,作点A关于直线l的对称点A',连接A'B,A'B与直线l的交点即为点P.
如图,在直线l同侧有两个定点A,B,在直线l上求作点P,使得|PA-PB|的值最大. 如图,连接BA并延长,BA的延长线与直线l的交点即为点P.
如图,在直线l两侧各有一个定点A,B,在直线l上求作点P,使得|PA-PB|的值最大. 如图,作点B关于直线l的对称点B',连接AB'并延长,AB'的延长线与直线l的交点即为点P.
如图,在直线l同侧有两个定点A,B,在直线l上求作点P,使得|PA-PB|的值最小. 如图,连接AB,作线段AB的垂直平分线,该线与直线l的交点即为点P,此时|PA-PB|=0.
11.> ∵y=(x-3)2+2,∴抛物线的对称轴为直线x=3,抛物线开口向上.∵点A(x1,y1),B(x2,y2)在二次函数y=(x-3)2+2的图象上,且x1
快解妙解
∵x1
12.20 ∵迎水坡AB的坡度i=1∶,∴=,∴AC=BC=10(米),在Rt△ABC中,由勾股定理,得AB===20(米).
13.8 如图,连接OB,过点O作OC⊥AB于点D,交☉O于点C.∵AB=24 cm,∴BD=AB=12 cm.∵OB=OC=13 cm,∴在Rt△OBD中,OD===5(cm),
∴CD=OC-OD=13-5=8(cm).
14.- 如图,连接B'D,BD,由题意可得BC=B'C',AC=A'C',∠BDB'=90°.∵D为AC的中点,∴C'D=CD=AC=1.在Rt△BCD中,由勾股定理,得BD==
=,∴S扇形BDB'==.又易知S△DCB'+S△BCD=S梯形CDC'B'=C'D×(CD+C'B')=
×1×3=,∴S阴影=S扇形BDB'-(S△DCB'+S△BCD)=-.
15.(,2)或(,2) 连接OD(图略),由题意可知,四边形OFDE是矩形,∴OD=EF.根据垂线段最短,可得当OD⊥AC时,OD最短,此时EF最短.在Rt△AOC中,∵OC=OA=4,∴当D是AC的中点时,OD⊥AC.∵DF∥OC,∴DF=OC=2,∴点P的纵坐标是2.∵点A的坐标为(4,0),且OA=OC=4OB,∴点B的坐标为(-1,0),点C的坐标为(0,4).设过A,B,C三点的抛物线的函数解析式为y=ax2+bx+4,把A,B的坐标分别代入可得a=-1,b=3,∴抛物线的函数解析式为 y=-x2+3x+4.当y=2时,x2-3x-2=0,解得x=.∴当线段EF的长度最短时,点P的坐标为(,2)或(,2).
16.【参考答案】(1)把(-2,5)代入二次函数y=x2+bx-3,
得5=4-2b-3,
∴b=-2. (3分)
(2)y1,y2,y3不能作为同一个三角形三边的长.
理由:把P1(4,y1),P2(5,y2),P3(6,y3)的坐标代入y=x2-2x-3,得y1=5,y2=12,y3=21.
∵5+12<21,
∴y1,y2,y3不能作为同一个三角形三边的长. (7分)
17.【参考答案】 如图,过A点作AE⊥BD交BD的延长线于E点.
∴∠AED=∠C=90°.
在Rt△BDC中,∠BDC=60°,
∴cos∠BDC==. (2分)
设CD=a,则BD=2a.
在Rt△BDC中,由勾股定理,得BC=a.
∵AD=2BD,
∴AD=4a,
∴AC=5a. (4分)
在Rt△ACB中,由勾股定理,得AB=2a.
在Rt△ADE中,sin∠ADE==,
∴AE=2a. (6分)
在Rt△ABE中,sin∠ABD==. (7分)
18.【解题思路】(1)连接OD,先得出OD∥AC,然后由∠C=90°得出OD⊥BC即可;(2)设☉O的半径为r,根据勾股定理列方程,求解即可.
【参考答案】(1)相切. (1分)
理由:如图,连接OD, ∵OA=OD,
∴∠OAD=∠ODA.
∵AD平分∠CAB,
∴∠OAD=∠CAD,
∴∠ODA=∠CAD,
∴OD∥AC.
∵∠C=90°,
∴∠ODB=90°,即OD⊥BC.
∵OD为☉O的半径,
∴直线BC与☉O的位置关系是相切. (4分)
(2)设☉O的半径为r,则OD=OF=r. (5分)
在Rt△BDO中,由勾股定理,得OB2=BD2+OD2,
即(r+2)2=(2)2+r2,解得r=2.
即☉O的半径是2. (8分)
19.【参考答案】 (1)根据题意设y关于x的函数表达式为y=a(x-3)2+3,
把(0,)代入表达式,得=a(0-3)2+3,
解得a=-,
∴y关于x的函数表达式为y=-(x-3)2+3. (4分)
(2)该女生在此项考试中是得满分,
理由:令y=0,则-(x-3)2+3=0,
解得x1=7.5,x2=-1.5(舍去).
∵7.5>6.70,
∴该女生在此项考试中是得满分. (8分)
20.【参考答案】 (1)∵∠ADC=84°,∠ABC=37°,
∴∠BAD=∠ADC-∠ABC=47°. (3分)
(2)在Rt△ABC中,tan∠ABC=tan 37°=,
∴BC=.
同理,在Rt△ADC中,DC=.
∵BD=4米,
∴BC-DC=-=BD=4米,
∴AC-AC≈4米,
∴AC≈3.3米.
答:表AC的长约是3.3米. (10分)
21.【参考答案】(1)证明:∵AC∥BE,
∴∠E=∠ACD.
∵点D,C为的三等分点,
∴==,
∴∠A=∠ACD,
∴∠E=∠A. (5分)
(2)由(1)知==,
∴∠D=∠CBD=∠A=∠E,
∴BE=BD=5,BC=CD=3,△CBD∽△BDE,
∴=,即=,
解得DE=,
∴CE=DE-CD=-3=. (11分)
22.【参考答案】 (1)∵A(1,0),AB=4,
∴B(-3,0).
将A(1,0),B(-3,0)分别代入y=x2+bx+c,
得解得
故抛物线的解析式为y=x2+2x-3. (5分)
(2)∵y=x2+2x-3=(x+1)2-4,
∴C(-1,-4).
设P(m,0),则AP=1-m.
由PQ∥BC,易得△APQ∽△ABC,
∴=()2=()2=.
又S△ABC=×4×4=8,
∴S△APQ=8×=,
∴S△CPQ=S△APC-S△APQ=×(1-m)×4-=-(m+1)2+2. (9分)
∵-<0,
∴当m=-1时,S△CPQ最大,最大值为2, (10分)
此时点P的坐标为(-1,0). (11分)
23.【解题思路】 (1)根据三角形相似可知,即点D是OC的中点,进而得到DC=OC;(2)过点N作ND⊥OH于点D,说明△NHD是等腰直角三角形,得ND=HD,借助tan∠COH=表示出ND,OD,再根据勾股定理求解;(3)当点M与点O重合时,点N也与点O重合,当点M运动至点B时,点N运动至点T,故点N的运动路径长为OA+的长.
【参考答案】 (1)∵OM=1.6,DF=0.8,EF∥AB,
∴△CDF∽△COM,
∴=.
∵OM=1.6,DF=0.8,
∴==,
∴CD=OC.
∵OC=OA=4,
∴CD=2. (4分)
(2)如图,过点N作ND⊥OH于点D.
∵∠OHN=45°,
∴△NHD是等腰直角三角形,
∴ND=HD.
∵tan∠COH=,∠NDO=90°,
∴=.
设ND=3x=HD,则OD=4x.
∵OH=OA=4,
∴OH=3x+4x=4,
∴x=,
∴ND=×3=,OD=×4=,
∴ON==. (8分)
(3)如图,当点M与点O重合时,点N也与点O重合,当点M运动至点B时,点N运动至点T,故点N的运动路径长为OA+的长.
∵∠HOM=50°,OH=OB,
∴∠OHB=∠OBH=65°.
∵∠OHM=∠OHT,OH=OT,
∴∠OTH=∠OHT=65°,
∴∠TOH=50°,
∴∠AOT=180°-50°-50°=80°,
∴的长==π,
∴点N的运动路径长=4+π. (13分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
