2024北师版九年级数学下学期期中综合测试卷(含答案)
文档属性
| 名称 | 2024北师版九年级数学下学期期中综合测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-11 16:14:35 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024北师版九年级数学下学期单元测试卷
期中综合测试卷
时间:100分钟 满分:120分
题号 一 二 三 评价
错题
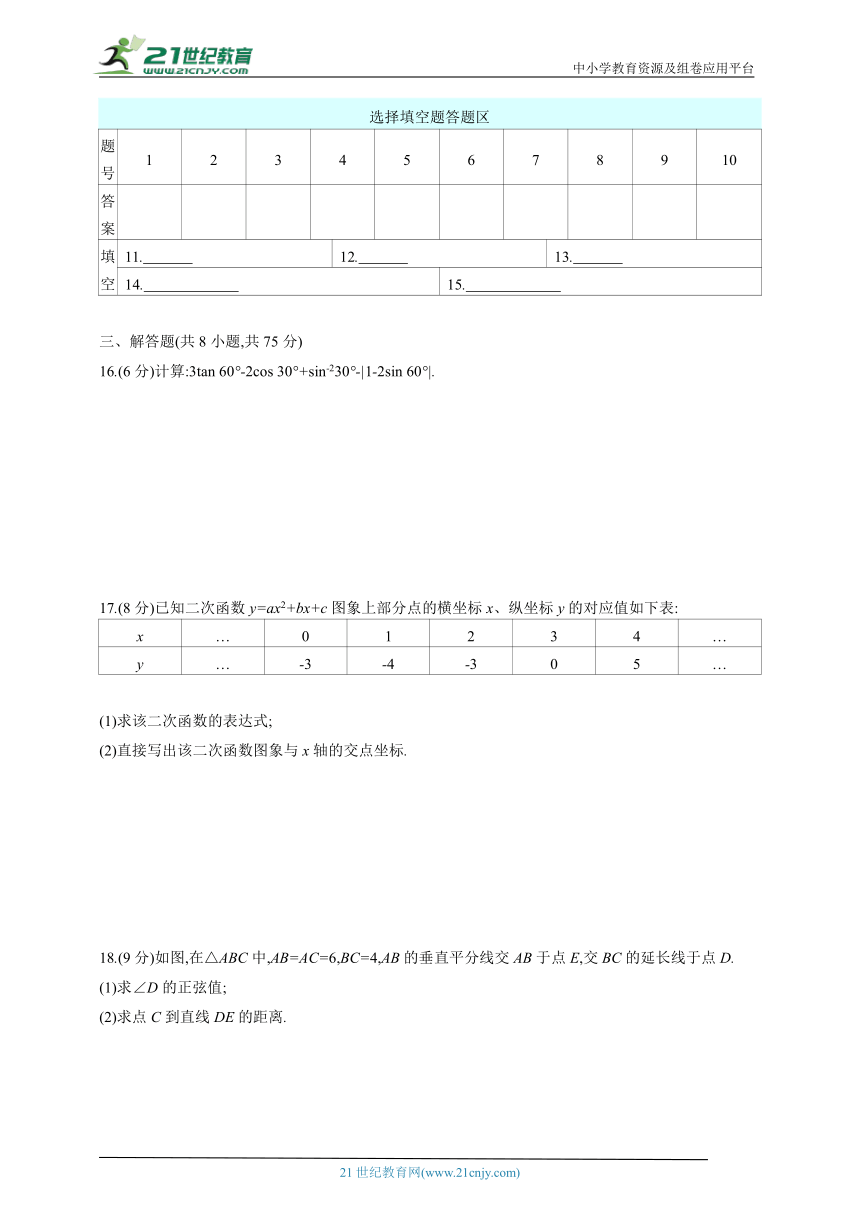
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.抛物线y=(x+2)2+3的顶点坐标是 ( )
A.(-2,-3) B.(-2,3)
C.(2,-3) D.(2,3)
2.如图,P是∠α的边OA上一点,点P的坐标为(12,5),则tan α=( )
A. B.
C. D.
3.若点(0,a),(4,b)都在二次函数y=(x-2)2的图象上,则a与b的大小关系是 ( )
A.a>b B.aC.a=b D.无法确定
4.某公园准备制作一批如图所示的景点指示牌,若指示牌的倾斜角为α,铅直高度为h,则指示牌的边AB的长等于 ( )
A.hsin α B. C.hcos α D.
5.二次函数y=ax2-1与正比例函数y=ax在同一平面直角坐标系中的图象可能是 ( )
A B C D
6.如图,在正方形网格中,已知△ABC的三个顶点均在格点上,则∠ACB的余弦值为 ( )
A. B. C. D.2
7.已知将二次函数y=x2+bx+c的图象向右平移2个单位长度,再向下平移3个单位长度,所得图象的表达式为y=x2-4x-5,则b,c的值为( )
A.b=0,c=11 B.b=-8,c=-7
C.b=0,c=-6 D.b=-8,c=5
8.一枚炮弹向上发射x s时的高度为y m,且时间与高度的关系为y=ax2+bx(a≠0).若此炮弹在发射7 s与14 s时的高度相等,则在下列哪个时刻中,炮弹的高度最高 ( )
A.8 s B.10 s C.12 s D.15 s
9.图(1)是某种路灯的实物图片,图(2)是该路灯的平面示意图,MN为立柱的一部分,灯臂AC,支架BC与立柱MN分别交于A,B两点,灯臂AC与支架BC交于点C,已知∠MAC=60°,∠ACB=15°,AC=40 cm,则支架BC的长为( )
(结果精确到1 cm,参考数据:≈1.414,≈1.732,≈2.449)
A.47 cm B.48 cm C.49 cm D.50 cm
10.二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=,且图象经过点(2,0).下列说法:①abc<0;②-2b+c=0;③4a+2b+c<0;④若y<0,则x>2;⑤b+c>m(am+b)+c(其中m≠).其中正确的有 ( )
A.5个 B.4个 C.3个 D.2个
二、填空题(共5小题,每小题3分,共15分)
11.在Rt△ABC中,AC=BC,则cos A= .
12.写出一组a,b的值,使二次函数y=ax2+bx+2的图象与x轴有两个不同的交点,则a,b的值可以是a= ,b= .
13.图(1)是一个倾斜角为α的斜坡的横截面,tan α=,斜坡顶端B与地面的距离BC为3米.为了对这个斜坡上的绿地进行喷灌,在斜坡底端安装了一个喷头A,喷头A喷出的水珠在空中走过的曲线可以看作抛物线的一部分.设喷出水珠的竖直高度为y(单位:米)(水珠的竖直高度是指水珠与地面的距离),水珠与喷头A的水平距离为x(单位:米),y与x之间近似满足函数关系y=ax2+bx(a,b是常数,a≠0),图(2)记录了x与y的相关数据,则y与x的函数关系式为 .
图(1) 图(2)
14.我国魏晋时期的数学家赵爽在为天文学著作《周髀算经》作注解时,用4个全等的直角三角形和中间的小正方形拼成一个大正方形,这个图被称为“弦图”,它体现了中国古代数学的成就.如图,已知大正方形ABCD的面积是100,小正方形EFGH的面积是4,那么sin∠ADF= .
15.已知在x轴上有线段AB,且AB的长为2,以AB为边作等边三角形ABC,使点C落在二次函数y=x2-2x-2的图象上,则点C的坐标为 .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15.
三、解答题(共8小题,共75分)
16.(6分)计算:3tan 60°-2cos 30°+sin-230°-|1-2sin 60°|.
17.(8分)已知二次函数y=ax2+bx+c图象上部分点的横坐标x、纵坐标y的对应值如下表:
x … 0 1 2 3 4 …
y … -3 -4 -3 0 5 …
(1)求该二次函数的表达式;
(2)直接写出该二次函数图象与x轴的交点坐标.
18.(9分)如图,在△ABC中,AB=AC=6,BC=4,AB的垂直平分线交AB于点E,交BC的延长线于点D.
(1)求∠D的正弦值;
(2)求点C到直线DE的距离.
19.(9分)某药店购进一批医用级消毒液,进价为15元/瓶,出售时售价最低为18元/瓶,且相关部门规定利润率不能高于40%.该药店通过分析销售情况,发现这种消毒液一天的销售量y(瓶)与当天的售价x(元/瓶)之间满足一次函数关系,其图象如图所示.
(1)求y与x之间的函数关系式;
(2)设该药店某天销售这种消毒液所获得的利润为w元,写出w与x的函数关系式,当售价定为多少时,可获得日销售利润最大,最大日销售利润是多少元
20.(10分)位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.
某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16 m到达点N处,测得点A的仰角为45°.测角仪的高度为1.6 m.
(1)求观星台最高点A距离地面的高度(结果精确到 0.1 m.参考数据:sin 22°≈0.37,cos 22°≈0.93,tan 22°≈0.40,≈1.41);
(2)“景点简介”显示,观星台的高度为12.6 m.请计算本次测量结果的误差,并提出一条减小误差的合理化建议.
21.(10分)已知抛物线y=-x2+bx+c的顶点坐标为(1,3).
(1)求b,c的值.
(2)直线l交抛物线于点A(-2,m),B(n,2).若点P在抛物线上且位于直线l的上方(不与点A,B重合),求点P的纵坐标yP的取值范围.
22.(11分)东西走向海岸线上有一个码头(图中线段AB),已知AB的长为132米,小明在A处测得海上一艘货船M在A的东北方向,小明沿海岸线向东走60米后到达点C,在C测得M在C处的北偏东15°方向(参考数据:≈1.41,≈1.73,≈2.45)
(1)求AM的长;(结果精确到1米)
(2)如图,货船从M出发,沿着南偏东30°方向行驶,问该货船是否能行驶到码头所在的线段AB上,请说明理由.
23.(12分)如图,在平面直角坐标系中,点A的坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O出发沿着OA平移,与直线x=2相交于点P,顶点M到点A时停止移动.
(1)求线段OA所在直线的函数表达式.
(2)抛物线在平移的过程中,求点P到x轴的最短距离.
(3)当线段PB最短时,平移后的抛物线上是否存在点Q,使△QMA与△PMA的面积相等 若存在,请求出点Q的坐标;若不存在,请说明理由.
九年级下册期中综合测试卷
选择填空题答案速查
1 2 3 4 5 6 7 8 9 10
B A C B B C C B C C
11. 12.1 3 (答案不唯一) 13.y=-x2+2x
14. 15.(1+, 3),(1-, 3)或(1,-3)
1.B
2.A 如图,过点P作PH⊥x轴于点H,则∠OHP=90°.∵点P(12,5),∴PH=5,OH=12.在Rt△OHP中,tan α==.故选A.
3.C ∵y=(x-2)2,∴抛物线开口向上,对称轴是直线x=2,∴点(0,a),(4,b)离直线x=2一样近,∴a=b.
快解妙解
(直接代入法)分别将x=0,x=4代入y=(x-2)2,得a=4,b=4,∴a=b.
4.B 如图,过点A作AC⊥BC于C.在Rt△ABC中,AC=h,∠B=α,则sin α=.所以AB=.故选B.
5.B 由二次函数y=ax2-1可知抛物线与y轴交于点(0,-1),故C,D选项中的图象不符合题意;由A选项中的抛物线可知a>0,由直线可知a<0,故A中的图象不符合题意;由B选项中的抛物线可知a>0,由直线可知a>0,故B中的图象符合题意.
一题多解
令a=1,简单画出草图,看是否有符合的选项,如果没有,再令a=-1,用同样的方法作出判断.
6.C 如图,取格点D,连接BD,AD.∵∠CBF=∠EBD=45°,∠EBF=90°,∴∠CBD=180°,∴C,B,D三点在一条直线上.∵∠BDE=45°,∠ADE=45°,∴∠ADC=90°.若设正方形网格边长为1,则AD=,CD==2,AC==,∴cos∠ACB===.
7.C 将二次函数y=x2-4x-5配方成顶点式,得y=(x-2)2-9,把该抛物线向左平移2个单位长度,再向上平移3个单位长度得到y=x2-6的图象,即y=x2+bx+c=x2-6,所以b=0,c=-6.
8.B 根据抛物线的对称性,由于炮弹在发射7 s与14 s时的高度相等,则当x==10.5时,炮弹达到最高点
由题意知,该抛物线开口向下,所以到直线x=10.5的距离越近的点对应的y值越大,故选B.
9.C 如图,过点C作CD⊥MN于D,则∠CDB=90°.∵∠CAD=60°,AC=40 cm,∴CD=AC·sin∠CAD=40×sin 60°=40×=20(cm).∵∠ACB=15°,∴∠CBD=∠CAD-∠ACB=60°-15°=45°,∴BC=CD=×20=20≈20×2.449≈49(cm).
10.C ∵抛物线开口向下,且交y轴于正半轴,∴a<0,c>0.∵对称轴是直线x=-=,即b=-a,∴b>0,∴abc<0,故①正确;∵二次函数y=ax2+bx+c(a≠0)的图象过点(2,0),∴0=4a+2b+c,故③不正确;又b=-a,∴0=-4b+2b+c,即-2b+c=0,故②正确;∵抛物线开口向下,对称轴是直线x=,且图象经过点(2,0),∴抛物线与x轴的另一个交点为(-1,0),∴若y<0,则x>2或x<-1,故④不正确;∵抛物线开口向下,对称轴是直线x=,∴当x=时,y取得最大值,ymax=()2a+b+c=-b+b+c=b+c;当x=m时,
ym=am2+bm+c=m(am+b)+c.∵m≠,∴ymax>ym,故⑤正确.综上,说法①②⑤正确,故选C.
11.
12.1 3(答案不唯一,b2-8a>0即可) ∵二次函数y=ax2+bx+2(a≠0)的图象与x轴有两个不同的交点,∴Δ=b2-8a>0,若a=1,则b可取3.
13.y=-x2+2x 在Rt△ABC中,tan α=,BC=3,∴AC=6,∴点B的坐标为(6,3).∵B(6,3),E(4,4)在抛物线y=ax2+bx上,∴解得
∴y关于x的函数关系式为y=-x2+2x.
14. ∵大正方形ABCD的面积是100,∴AD=10.∵小正方形EFGH的面积是4,∴小正方形EFGH的边长为2,∴DF-AF=2,设AF=x,则DF=x+2,由勾股定理得,x2+(x+2)2=102,解得x=6或x=-8(负值舍去),∴AF=6,∴sin∠ADF===.
15.(1+, 3),(1-, 3)或(1,-3) 设AB边上的高为h,因为△ABC是等边三角形,且AB=2,所以h=3.设点C的纵坐标为y,因为点C在二次函数的图象上,所以|y|=3,所以y=±3.把y=3代入y=x2-2x-2,得x2-2x-2=3,解得x1=1+,x2=1-;把y=-3代入y=x2-2x-2,得x2-2x-2=-3,解得x3= x4=1.综上可知,点C的坐标为(1+,3),(1-,3)或(1,-3)
16.【参考答案】原式=3-2×+()-2-|1-2×| (2分)
=3-+4-(-1+) (4分)
=2+4+1- (5分)
=5+. (6分)
高分锦囊
本题涉及特殊角的三角函数值和实数的综合运算,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,对于能化简的代数式应先化简后代入,这样可使运算简便快捷.
17.【参考答案】 (1)∵抛物线经过点(0,-3),(2,-3),(1,-4),
∴抛物线的对称轴为直线x=1,顶点坐标为(1,-4).
设抛物线解析式为y=a(x-1)2-4,
把(0,-3)代入得a(0-1)2-4=-3,
解得a=1,
∴抛物线解析式为y=(x-1)2-4. (4分)
(2)∵抛物线与x轴的一个交点坐标为(3,0),
而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点坐标为(-1,0),
即该二次函数图象与x轴的交点坐标为(-1,0),(3,0). (8分)
18.【参考答案】 (1)如图,过点A作AH⊥BC于点H.
∵AB=AC,BC=4,
∴BH=BC=2. (2分)
在△ABH中,∠BHA=90°,AB=6,
∴sin∠BAH===.
∵DE是AB的垂直平分线,
∴∠BED=90°,BE=3,
∴∠BED=∠BHA.
∵∠B=∠B,
∴∠BAH=∠D,
∴sin∠D=sin∠BAH=,即∠D的正弦值为. (5分)
(2)过点C作CM⊥DE于点M.
在△BED中,∠BED=90°,sin∠D=,BE=3,
∴BD==9,
∴CD=BD-BC=9-4=5. (7分)
在△MCD中,∠CMD=90°,sin∠D==,
∴CM=CD=,
即点C到DE的距离为. (9分)
19.【参考答案】 (1)设y与x之间的函数关系式为y=kx+b(k≠0),
将(18,24),(20,20)代入y=kx+b,
得
解得
∴y与x之间的函数关系式为y=-2x+60. (4分)
∵利润不能高于40%,
∴x≤15×(1+40%),即x≤21(18≤x≤21,且x为整数). (6分)
(2)依题意得w=(x-15)(-2x+60)=-2x2+90x-900=-2(x-22.5)2+112.5.
∵-2<0,18≤x≤21,且x为整数,
∴当x=21时,w取得最大值,最大值为108,
∴当每瓶消毒液售价为21元时,药店销售该消毒液每天销售利润最大,最大利润是108元. (10分)
20.【参考答案】(1)如图,过点A作AF⊥MP,垂足为点F,交BC的延长线于点E.
由题意知,四边形MBCN和四边形NCEF均为矩形. (2分)
设AE=x m,
在Rt△ACE中,∠AEC=90°,∠ACE=45°,
∴CE=AE=x m.
在Rt△ABE中,∠AEB=90°,∠ABE=22°.
∵tan 22°=,
∴BE=≈=x(m). (4分)
∵BE-CE=BC,
∴x-x=16,
解得x≈10.67. (5分)
∵EF=BM=1.6 m,
∴AF=AE+EF=10.67+1.6≈12.3(m).
即观星台最高点A距离地面的高度约为12.3 m. (7分)
(2)误差为12.6-12.3=0.3(m). (8分)
可多次测量,取测量数据的平均值(答案不唯一,合理即可).(10分)
高分锦囊
解直角三角形的实际应用题的解题通法
(1)应用“解直角三角形”的模型解决问题,关键是把已知角或特殊角放在直角三角形中,当两个直角三角形有公共边时,公共边是联系两个直角三角形的纽带,通常要求出这条公共边的长度,进而解决问题.
(2)当图形中没有直角三角形时,则需要根据实际情况构造直角三角形.
(3)运用“解直角三角形”的模型解决实际问题的步骤:①审题,根据题干,弄明白图形中哪些是已知量,哪些是未知量;②将已知条件转化到示意图中,把实际问题转化为解直角三角形的问题;③选择适当的关系式解直角三角形.
21.【参考答案】 (1)∵抛物线y=-x2+bx+c的顶点坐标为(1,3),
∴顶点式为y=-(x-1)2+3.
∵y=-(x-1)2+3=-x2+2x+2,
∴b=2,c=2. (3分)
(2)由(1)可知抛物线为y=-x2+2x+2,
∵直线l交抛物线于点A(-2,m),B(n,2),
将x=-2代入y=-x2+2x+2,
y=-(-2)2+2×(-2)+2=-6,即m=-6,
∴点A坐标为(-2,-6).
将y=2代入y=-x2+2x+2,得2=-x2+2x+2,
解得x=0或x=2,即n=0或n=2,
∴点B坐标为(0,2)或 (2,2). (5分)
①点A坐标为(-2,-6),点B坐标为(0,2),
设直线l的解析式为y=k1x+b1,
将(-2,-6)和(0,2)代入y=k1x+b1,
解得
∴直线l的解析式为y=4x+2.
∵点P在抛物线上且位于直线l的上方且不与点A,B重合,
设点P坐标为(xP,yP),
∴-+2xP+2>4xP+2,解得-2∵二次函数对称轴为x=1,开口向下,
∴在-2∴-6②点A坐标为(-2,-6),点B坐标为(2,2),
设直线L的解析式为y=k2x+b2,
将(-2,-6)和(2,2)代入y=k2x+b2,
解得
∴直线l的解析式为y=2x-2.
∵点P在抛物线上且位于直线L的上方且不与点A,B重合,
设点P坐标为(xP,yP),
∴-+2xP+2>2xP-2,解得-2∵二次函数对称轴为x=1,开口向下,
∴在-2在1∴-6综上,点P的纵坐标yP的取值范围为-622.【解题思路】(1)过点C作CD⊥AM,垂足为D,在Rt△ADC中,求AD,CD的长,在Rt△CDM中,求DM的长.(2)过点M作MF⊥AB,垂足为F,设货船从M出发,沿着南偏东30°方向行驶,交线段AB所在的直线于点G,在Rt△AMF中,求出MF,AF的长,在Rt△MGF中,求出GF的长,从而求出AG的长, 比较后可得到答案.
【参考答案】 (1)如图,过点C作CD⊥AM,垂足为D.
∠MAC=90°-45°=45°,∠ACM=90°+15°=105°,
∴∠AMC=180°-∠MAC-∠ACM=30°.
在Rt△ADC中,AC=60米,
∴AD=AC·cos 45°=60×=30(米),
CD=AC·sin 45°=60×=30(米). (3分)
在Rt△CDM中,DM===30(米),
∴AM=AD+DM=30+30≈116(米).
∴AM的长约为116米. (6分)
(2)该货船能行驶到码头所在的线段AB上.
理由:过点M作MF⊥AB,垂足为F,设货船从M出发,沿着南偏东30°方向行驶,交线段AB所在的直线于点G.
由题意得∠FMG=30°. (7分)
在Rt△AMF中,AM=(30+30)米,∠MAF=45°,
∴AF=AM·cos 45°=(30+30)×=(30+30)(米),
FM=AM·sin 45°=(30+30)×=(30+30)(米).
在Rt△MGF中,FG=MF·tan 30°=(30+30)×=(10+30)(米).
∴AG=AF+FG=30+30+10+30=60+40≈129.2(米). (10分)
∵AB=132米,
且132>129.2,
∴该货船能行驶到码头所在的线段AB上. (11分)
23.【解题思路】(1)根据点A的坐标,用待定系数法求出线段OA所在直线的函数表达式.(2)设点M的横坐标为m,把PB的长用含m的式子表示,根据二次函数的性质求解即可.(3)分两种情况讨论:①当点Q在直线OA下方时,求出点Q的坐标并进行判断;②当点Q在直线OA上方时,求出点Q的坐标.
【参考答案】(1)设线段OA所在直线的函数表达式为y=kx(k≠0),
把点A的坐标(2,4)代入,得4=2k,解得k=2,
故线段OA所在直线的函数表达式为y=2x. (2分)
(2)设抛物线顶点M的横坐标为m,
∵点M在线段OA上,
∴顶点M的坐标为(m,2m),
∴抛物线的表达式为y=(x-m)2+2m. (3分)
当x=2时,y=(2-m)2+2m=m2-2m+4(0≤m≤2),
∴点P的坐标为(2,m2-2m+4),
PB=m2-2m+4=(m-1)2+3. (5分)
∵0≤m≤2,
∴当m=1时,PB的值最小,为3,
故点P到x轴的最短距离是3. (6分)
(3)存在. (7分)
当线段PB最短时,抛物线的表达式为y=(x-1)2+2,
设Q(x,x2-2x+3).
①当点Q在线段OA的下方时,过点P作直线PC∥AO,交y轴于点C,如图所示. (8分)
∵PB=3,AB=4,
∴AP=1,
∴OC=1,
∴点C的坐标为(0,-1).
∵点P的坐标为(2,3),
∴直线PC的函数表达式为y=2x-1.
∵S△QMA=S△PMA,
∴点Q在直线PC上,
∴x2-2x+3=2x-1,解得x1=x2=2,故点Q(2,3),
此时点Q与点P重合,
∴这样的点Q不存在. (9分)
②当点Q落在线段OA的上方时,作点P关于点A的对称点D,过点D作直线DE∥AO,交y轴于点E,如图所示. (10分)
∵AP=1,
∴EO=DA=1,
∴E,D的坐标分别是(0,1),(2,5),
∴直线DE的函数表达式为y=2x+1.
∵S△QMA=S△PMA,
∴点Q落在直线y=2x+1上,
∴x2-2x+3=2x+1,
解得x1=2+,x2=2-.
代入y=2x+1,得y1=5+2,y2=5-2,
∴此时抛物线上存在点Q1(2+,5+2),Q2(2-,5-2)使△QMA与△PMA的面积相等. (12分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师版九年级数学下学期单元测试卷
期中综合测试卷
时间:100分钟 满分:120分
题号 一 二 三 评价
错题
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.抛物线y=(x+2)2+3的顶点坐标是 ( )
A.(-2,-3) B.(-2,3)
C.(2,-3) D.(2,3)
2.如图,P是∠α的边OA上一点,点P的坐标为(12,5),则tan α=( )
A. B.
C. D.
3.若点(0,a),(4,b)都在二次函数y=(x-2)2的图象上,则a与b的大小关系是 ( )
A.a>b B.a
4.某公园准备制作一批如图所示的景点指示牌,若指示牌的倾斜角为α,铅直高度为h,则指示牌的边AB的长等于 ( )
A.hsin α B. C.hcos α D.
5.二次函数y=ax2-1与正比例函数y=ax在同一平面直角坐标系中的图象可能是 ( )
A B C D
6.如图,在正方形网格中,已知△ABC的三个顶点均在格点上,则∠ACB的余弦值为 ( )
A. B. C. D.2
7.已知将二次函数y=x2+bx+c的图象向右平移2个单位长度,再向下平移3个单位长度,所得图象的表达式为y=x2-4x-5,则b,c的值为( )
A.b=0,c=11 B.b=-8,c=-7
C.b=0,c=-6 D.b=-8,c=5
8.一枚炮弹向上发射x s时的高度为y m,且时间与高度的关系为y=ax2+bx(a≠0).若此炮弹在发射7 s与14 s时的高度相等,则在下列哪个时刻中,炮弹的高度最高 ( )
A.8 s B.10 s C.12 s D.15 s
9.图(1)是某种路灯的实物图片,图(2)是该路灯的平面示意图,MN为立柱的一部分,灯臂AC,支架BC与立柱MN分别交于A,B两点,灯臂AC与支架BC交于点C,已知∠MAC=60°,∠ACB=15°,AC=40 cm,则支架BC的长为( )
(结果精确到1 cm,参考数据:≈1.414,≈1.732,≈2.449)
A.47 cm B.48 cm C.49 cm D.50 cm
10.二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=,且图象经过点(2,0).下列说法:①abc<0;②-2b+c=0;③4a+2b+c<0;④若y<0,则x>2;⑤b+c>m(am+b)+c(其中m≠).其中正确的有 ( )
A.5个 B.4个 C.3个 D.2个
二、填空题(共5小题,每小题3分,共15分)
11.在Rt△ABC中,AC=BC,则cos A= .
12.写出一组a,b的值,使二次函数y=ax2+bx+2的图象与x轴有两个不同的交点,则a,b的值可以是a= ,b= .
13.图(1)是一个倾斜角为α的斜坡的横截面,tan α=,斜坡顶端B与地面的距离BC为3米.为了对这个斜坡上的绿地进行喷灌,在斜坡底端安装了一个喷头A,喷头A喷出的水珠在空中走过的曲线可以看作抛物线的一部分.设喷出水珠的竖直高度为y(单位:米)(水珠的竖直高度是指水珠与地面的距离),水珠与喷头A的水平距离为x(单位:米),y与x之间近似满足函数关系y=ax2+bx(a,b是常数,a≠0),图(2)记录了x与y的相关数据,则y与x的函数关系式为 .
图(1) 图(2)
14.我国魏晋时期的数学家赵爽在为天文学著作《周髀算经》作注解时,用4个全等的直角三角形和中间的小正方形拼成一个大正方形,这个图被称为“弦图”,它体现了中国古代数学的成就.如图,已知大正方形ABCD的面积是100,小正方形EFGH的面积是4,那么sin∠ADF= .
15.已知在x轴上有线段AB,且AB的长为2,以AB为边作等边三角形ABC,使点C落在二次函数y=x2-2x-2的图象上,则点C的坐标为 .
选择填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15.
三、解答题(共8小题,共75分)
16.(6分)计算:3tan 60°-2cos 30°+sin-230°-|1-2sin 60°|.
17.(8分)已知二次函数y=ax2+bx+c图象上部分点的横坐标x、纵坐标y的对应值如下表:
x … 0 1 2 3 4 …
y … -3 -4 -3 0 5 …
(1)求该二次函数的表达式;
(2)直接写出该二次函数图象与x轴的交点坐标.
18.(9分)如图,在△ABC中,AB=AC=6,BC=4,AB的垂直平分线交AB于点E,交BC的延长线于点D.
(1)求∠D的正弦值;
(2)求点C到直线DE的距离.
19.(9分)某药店购进一批医用级消毒液,进价为15元/瓶,出售时售价最低为18元/瓶,且相关部门规定利润率不能高于40%.该药店通过分析销售情况,发现这种消毒液一天的销售量y(瓶)与当天的售价x(元/瓶)之间满足一次函数关系,其图象如图所示.
(1)求y与x之间的函数关系式;
(2)设该药店某天销售这种消毒液所获得的利润为w元,写出w与x的函数关系式,当售价定为多少时,可获得日销售利润最大,最大日销售利润是多少元
20.(10分)位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.
某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP上架设测角仪,先在点M处测得观星台最高点A的仰角为22°,然后沿MP方向前进16 m到达点N处,测得点A的仰角为45°.测角仪的高度为1.6 m.
(1)求观星台最高点A距离地面的高度(结果精确到 0.1 m.参考数据:sin 22°≈0.37,cos 22°≈0.93,tan 22°≈0.40,≈1.41);
(2)“景点简介”显示,观星台的高度为12.6 m.请计算本次测量结果的误差,并提出一条减小误差的合理化建议.
21.(10分)已知抛物线y=-x2+bx+c的顶点坐标为(1,3).
(1)求b,c的值.
(2)直线l交抛物线于点A(-2,m),B(n,2).若点P在抛物线上且位于直线l的上方(不与点A,B重合),求点P的纵坐标yP的取值范围.
22.(11分)东西走向海岸线上有一个码头(图中线段AB),已知AB的长为132米,小明在A处测得海上一艘货船M在A的东北方向,小明沿海岸线向东走60米后到达点C,在C测得M在C处的北偏东15°方向(参考数据:≈1.41,≈1.73,≈2.45)
(1)求AM的长;(结果精确到1米)
(2)如图,货船从M出发,沿着南偏东30°方向行驶,问该货船是否能行驶到码头所在的线段AB上,请说明理由.
23.(12分)如图,在平面直角坐标系中,点A的坐标为(2,4),直线x=2与x轴相交于点B,连接OA,抛物线y=x2从点O出发沿着OA平移,与直线x=2相交于点P,顶点M到点A时停止移动.
(1)求线段OA所在直线的函数表达式.
(2)抛物线在平移的过程中,求点P到x轴的最短距离.
(3)当线段PB最短时,平移后的抛物线上是否存在点Q,使△QMA与△PMA的面积相等 若存在,请求出点Q的坐标;若不存在,请说明理由.
九年级下册期中综合测试卷
选择填空题答案速查
1 2 3 4 5 6 7 8 9 10
B A C B B C C B C C
11. 12.1 3 (答案不唯一) 13.y=-x2+2x
14. 15.(1+, 3),(1-, 3)或(1,-3)
1.B
2.A 如图,过点P作PH⊥x轴于点H,则∠OHP=90°.∵点P(12,5),∴PH=5,OH=12.在Rt△OHP中,tan α==.故选A.
3.C ∵y=(x-2)2,∴抛物线开口向上,对称轴是直线x=2,∴点(0,a),(4,b)离直线x=2一样近,∴a=b.
快解妙解
(直接代入法)分别将x=0,x=4代入y=(x-2)2,得a=4,b=4,∴a=b.
4.B 如图,过点A作AC⊥BC于C.在Rt△ABC中,AC=h,∠B=α,则sin α=.所以AB=.故选B.
5.B 由二次函数y=ax2-1可知抛物线与y轴交于点(0,-1),故C,D选项中的图象不符合题意;由A选项中的抛物线可知a>0,由直线可知a<0,故A中的图象不符合题意;由B选项中的抛物线可知a>0,由直线可知a>0,故B中的图象符合题意.
一题多解
令a=1,简单画出草图,看是否有符合的选项,如果没有,再令a=-1,用同样的方法作出判断.
6.C 如图,取格点D,连接BD,AD.∵∠CBF=∠EBD=45°,∠EBF=90°,∴∠CBD=180°,∴C,B,D三点在一条直线上.∵∠BDE=45°,∠ADE=45°,∴∠ADC=90°.若设正方形网格边长为1,则AD=,CD==2,AC==,∴cos∠ACB===.
7.C 将二次函数y=x2-4x-5配方成顶点式,得y=(x-2)2-9,把该抛物线向左平移2个单位长度,再向上平移3个单位长度得到y=x2-6的图象,即y=x2+bx+c=x2-6,所以b=0,c=-6.
8.B 根据抛物线的对称性,由于炮弹在发射7 s与14 s时的高度相等,则当x==10.5时,炮弹达到最高点
由题意知,该抛物线开口向下,所以到直线x=10.5的距离越近的点对应的y值越大,故选B.
9.C 如图,过点C作CD⊥MN于D,则∠CDB=90°.∵∠CAD=60°,AC=40 cm,∴CD=AC·sin∠CAD=40×sin 60°=40×=20(cm).∵∠ACB=15°,∴∠CBD=∠CAD-∠ACB=60°-15°=45°,∴BC=CD=×20=20≈20×2.449≈49(cm).
10.C ∵抛物线开口向下,且交y轴于正半轴,∴a<0,c>0.∵对称轴是直线x=-=,即b=-a,∴b>0,∴abc<0,故①正确;∵二次函数y=ax2+bx+c(a≠0)的图象过点(2,0),∴0=4a+2b+c,故③不正确;又b=-a,∴0=-4b+2b+c,即-2b+c=0,故②正确;∵抛物线开口向下,对称轴是直线x=,且图象经过点(2,0),∴抛物线与x轴的另一个交点为(-1,0),∴若y<0,则x>2或x<-1,故④不正确;∵抛物线开口向下,对称轴是直线x=,∴当x=时,y取得最大值,ymax=()2a+b+c=-b+b+c=b+c;当x=m时,
ym=am2+bm+c=m(am+b)+c.∵m≠,∴ymax>ym,故⑤正确.综上,说法①②⑤正确,故选C.
11.
12.1 3(答案不唯一,b2-8a>0即可) ∵二次函数y=ax2+bx+2(a≠0)的图象与x轴有两个不同的交点,∴Δ=b2-8a>0,若a=1,则b可取3.
13.y=-x2+2x 在Rt△ABC中,tan α=,BC=3,∴AC=6,∴点B的坐标为(6,3).∵B(6,3),E(4,4)在抛物线y=ax2+bx上,∴解得
∴y关于x的函数关系式为y=-x2+2x.
14. ∵大正方形ABCD的面积是100,∴AD=10.∵小正方形EFGH的面积是4,∴小正方形EFGH的边长为2,∴DF-AF=2,设AF=x,则DF=x+2,由勾股定理得,x2+(x+2)2=102,解得x=6或x=-8(负值舍去),∴AF=6,∴sin∠ADF===.
15.(1+, 3),(1-, 3)或(1,-3) 设AB边上的高为h,因为△ABC是等边三角形,且AB=2,所以h=3.设点C的纵坐标为y,因为点C在二次函数的图象上,所以|y|=3,所以y=±3.把y=3代入y=x2-2x-2,得x2-2x-2=3,解得x1=1+,x2=1-;把y=-3代入y=x2-2x-2,得x2-2x-2=-3,解得x3= x4=1.综上可知,点C的坐标为(1+,3),(1-,3)或(1,-3)
16.【参考答案】原式=3-2×+()-2-|1-2×| (2分)
=3-+4-(-1+) (4分)
=2+4+1- (5分)
=5+. (6分)
高分锦囊
本题涉及特殊角的三角函数值和实数的综合运算,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,对于能化简的代数式应先化简后代入,这样可使运算简便快捷.
17.【参考答案】 (1)∵抛物线经过点(0,-3),(2,-3),(1,-4),
∴抛物线的对称轴为直线x=1,顶点坐标为(1,-4).
设抛物线解析式为y=a(x-1)2-4,
把(0,-3)代入得a(0-1)2-4=-3,
解得a=1,
∴抛物线解析式为y=(x-1)2-4. (4分)
(2)∵抛物线与x轴的一个交点坐标为(3,0),
而抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点坐标为(-1,0),
即该二次函数图象与x轴的交点坐标为(-1,0),(3,0). (8分)
18.【参考答案】 (1)如图,过点A作AH⊥BC于点H.
∵AB=AC,BC=4,
∴BH=BC=2. (2分)
在△ABH中,∠BHA=90°,AB=6,
∴sin∠BAH===.
∵DE是AB的垂直平分线,
∴∠BED=90°,BE=3,
∴∠BED=∠BHA.
∵∠B=∠B,
∴∠BAH=∠D,
∴sin∠D=sin∠BAH=,即∠D的正弦值为. (5分)
(2)过点C作CM⊥DE于点M.
在△BED中,∠BED=90°,sin∠D=,BE=3,
∴BD==9,
∴CD=BD-BC=9-4=5. (7分)
在△MCD中,∠CMD=90°,sin∠D==,
∴CM=CD=,
即点C到DE的距离为. (9分)
19.【参考答案】 (1)设y与x之间的函数关系式为y=kx+b(k≠0),
将(18,24),(20,20)代入y=kx+b,
得
解得
∴y与x之间的函数关系式为y=-2x+60. (4分)
∵利润不能高于40%,
∴x≤15×(1+40%),即x≤21(18≤x≤21,且x为整数). (6分)
(2)依题意得w=(x-15)(-2x+60)=-2x2+90x-900=-2(x-22.5)2+112.5.
∵-2<0,18≤x≤21,且x为整数,
∴当x=21时,w取得最大值,最大值为108,
∴当每瓶消毒液售价为21元时,药店销售该消毒液每天销售利润最大,最大利润是108元. (10分)
20.【参考答案】(1)如图,过点A作AF⊥MP,垂足为点F,交BC的延长线于点E.
由题意知,四边形MBCN和四边形NCEF均为矩形. (2分)
设AE=x m,
在Rt△ACE中,∠AEC=90°,∠ACE=45°,
∴CE=AE=x m.
在Rt△ABE中,∠AEB=90°,∠ABE=22°.
∵tan 22°=,
∴BE=≈=x(m). (4分)
∵BE-CE=BC,
∴x-x=16,
解得x≈10.67. (5分)
∵EF=BM=1.6 m,
∴AF=AE+EF=10.67+1.6≈12.3(m).
即观星台最高点A距离地面的高度约为12.3 m. (7分)
(2)误差为12.6-12.3=0.3(m). (8分)
可多次测量,取测量数据的平均值(答案不唯一,合理即可).(10分)
高分锦囊
解直角三角形的实际应用题的解题通法
(1)应用“解直角三角形”的模型解决问题,关键是把已知角或特殊角放在直角三角形中,当两个直角三角形有公共边时,公共边是联系两个直角三角形的纽带,通常要求出这条公共边的长度,进而解决问题.
(2)当图形中没有直角三角形时,则需要根据实际情况构造直角三角形.
(3)运用“解直角三角形”的模型解决实际问题的步骤:①审题,根据题干,弄明白图形中哪些是已知量,哪些是未知量;②将已知条件转化到示意图中,把实际问题转化为解直角三角形的问题;③选择适当的关系式解直角三角形.
21.【参考答案】 (1)∵抛物线y=-x2+bx+c的顶点坐标为(1,3),
∴顶点式为y=-(x-1)2+3.
∵y=-(x-1)2+3=-x2+2x+2,
∴b=2,c=2. (3分)
(2)由(1)可知抛物线为y=-x2+2x+2,
∵直线l交抛物线于点A(-2,m),B(n,2),
将x=-2代入y=-x2+2x+2,
y=-(-2)2+2×(-2)+2=-6,即m=-6,
∴点A坐标为(-2,-6).
将y=2代入y=-x2+2x+2,得2=-x2+2x+2,
解得x=0或x=2,即n=0或n=2,
∴点B坐标为(0,2)或 (2,2). (5分)
①点A坐标为(-2,-6),点B坐标为(0,2),
设直线l的解析式为y=k1x+b1,
将(-2,-6)和(0,2)代入y=k1x+b1,
解得
∴直线l的解析式为y=4x+2.
∵点P在抛物线上且位于直线l的上方且不与点A,B重合,
设点P坐标为(xP,yP),
∴-+2xP+2>4xP+2,解得-2
∴在-2
设直线L的解析式为y=k2x+b2,
将(-2,-6)和(2,2)代入y=k2x+b2,
解得
∴直线l的解析式为y=2x-2.
∵点P在抛物线上且位于直线L的上方且不与点A,B重合,
设点P坐标为(xP,yP),
∴-+2xP+2>2xP-2,解得-2
∴在-2
【参考答案】 (1)如图,过点C作CD⊥AM,垂足为D.
∠MAC=90°-45°=45°,∠ACM=90°+15°=105°,
∴∠AMC=180°-∠MAC-∠ACM=30°.
在Rt△ADC中,AC=60米,
∴AD=AC·cos 45°=60×=30(米),
CD=AC·sin 45°=60×=30(米). (3分)
在Rt△CDM中,DM===30(米),
∴AM=AD+DM=30+30≈116(米).
∴AM的长约为116米. (6分)
(2)该货船能行驶到码头所在的线段AB上.
理由:过点M作MF⊥AB,垂足为F,设货船从M出发,沿着南偏东30°方向行驶,交线段AB所在的直线于点G.
由题意得∠FMG=30°. (7分)
在Rt△AMF中,AM=(30+30)米,∠MAF=45°,
∴AF=AM·cos 45°=(30+30)×=(30+30)(米),
FM=AM·sin 45°=(30+30)×=(30+30)(米).
在Rt△MGF中,FG=MF·tan 30°=(30+30)×=(10+30)(米).
∴AG=AF+FG=30+30+10+30=60+40≈129.2(米). (10分)
∵AB=132米,
且132>129.2,
∴该货船能行驶到码头所在的线段AB上. (11分)
23.【解题思路】(1)根据点A的坐标,用待定系数法求出线段OA所在直线的函数表达式.(2)设点M的横坐标为m,把PB的长用含m的式子表示,根据二次函数的性质求解即可.(3)分两种情况讨论:①当点Q在直线OA下方时,求出点Q的坐标并进行判断;②当点Q在直线OA上方时,求出点Q的坐标.
【参考答案】(1)设线段OA所在直线的函数表达式为y=kx(k≠0),
把点A的坐标(2,4)代入,得4=2k,解得k=2,
故线段OA所在直线的函数表达式为y=2x. (2分)
(2)设抛物线顶点M的横坐标为m,
∵点M在线段OA上,
∴顶点M的坐标为(m,2m),
∴抛物线的表达式为y=(x-m)2+2m. (3分)
当x=2时,y=(2-m)2+2m=m2-2m+4(0≤m≤2),
∴点P的坐标为(2,m2-2m+4),
PB=m2-2m+4=(m-1)2+3. (5分)
∵0≤m≤2,
∴当m=1时,PB的值最小,为3,
故点P到x轴的最短距离是3. (6分)
(3)存在. (7分)
当线段PB最短时,抛物线的表达式为y=(x-1)2+2,
设Q(x,x2-2x+3).
①当点Q在线段OA的下方时,过点P作直线PC∥AO,交y轴于点C,如图所示. (8分)
∵PB=3,AB=4,
∴AP=1,
∴OC=1,
∴点C的坐标为(0,-1).
∵点P的坐标为(2,3),
∴直线PC的函数表达式为y=2x-1.
∵S△QMA=S△PMA,
∴点Q在直线PC上,
∴x2-2x+3=2x-1,解得x1=x2=2,故点Q(2,3),
此时点Q与点P重合,
∴这样的点Q不存在. (9分)
②当点Q落在线段OA的上方时,作点P关于点A的对称点D,过点D作直线DE∥AO,交y轴于点E,如图所示. (10分)
∵AP=1,
∴EO=DA=1,
∴E,D的坐标分别是(0,1),(2,5),
∴直线DE的函数表达式为y=2x+1.
∵S△QMA=S△PMA,
∴点Q落在直线y=2x+1上,
∴x2-2x+3=2x+1,
解得x1=2+,x2=2-.
代入y=2x+1,得y1=5+2,y2=5-2,
∴此时抛物线上存在点Q1(2+,5+2),Q2(2-,5-2)使△QMA与△PMA的面积相等. (12分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
