三角函数图象(广西壮族自治区玉林市)
文档属性
| 名称 | 三角函数图象(广西壮族自治区玉林市) |  | |
| 格式 | rar | ||
| 文件大小 | 423.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-03-22 23:02:00 | ||
图片预览




文档简介
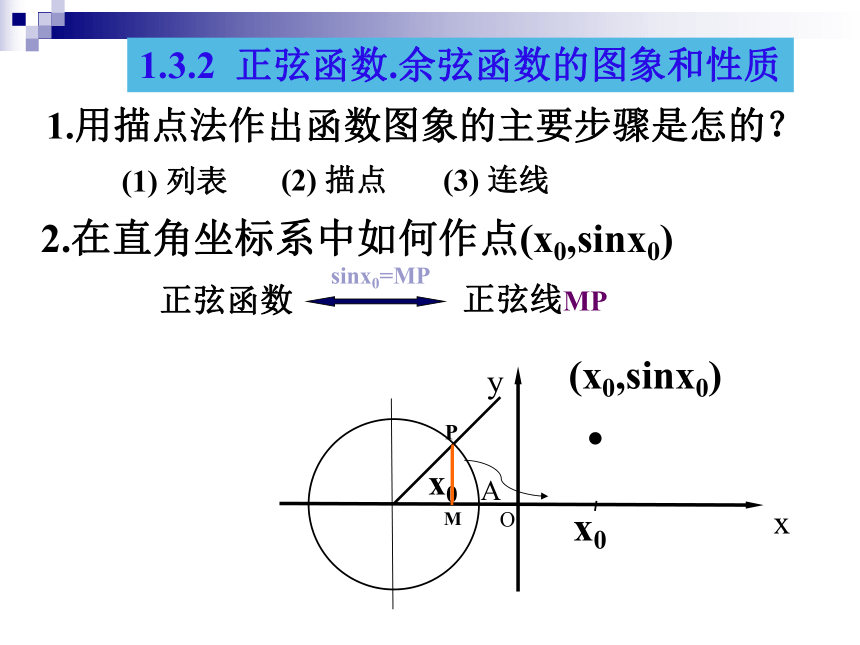
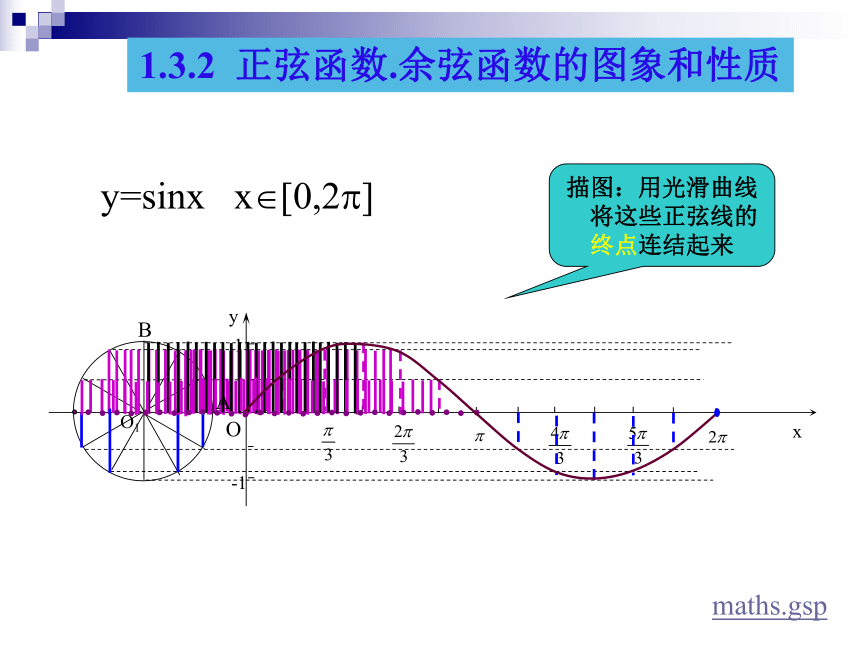
课件15张PPT。正弦图像之应用:例子一正弦图像之应用:例子二高流中学 数学组1.3.2 正弦函数.余弦函数的图象和性质(1) 列表(2) 描点(3) 连线1.用描点法作出函数图象的主要步骤是怎的?正弦、余弦函数的图象2.在直角坐标系中如何作点(x0,sinx0) xyOPx0M正弦函数正弦线MPsinx0=MP.(x0,sinx0)x0A1.3.2 正弦函数.余弦函数的图象和性质 正弦、余弦函数的图象 y=sinx x?[0,2?] O 描图:用光滑曲线
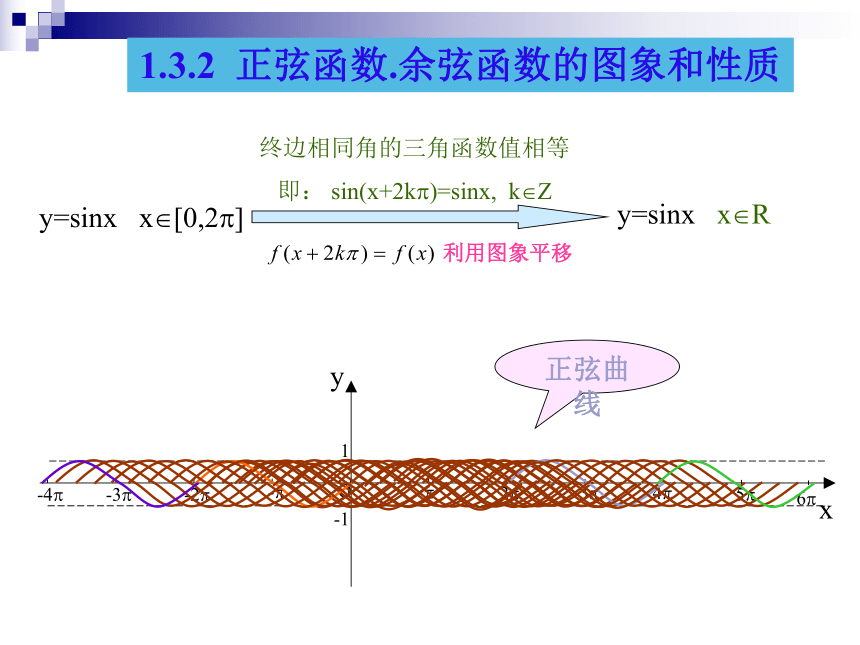
将这些正弦线的终点连结起来AB1.3.2 正弦函数.余弦函数的图象和性质maths.gspy=sinx x?[0,2?]y=sinx x?R终边相同角的三角函数值相等 即: sin(x+2k?)=sinx, k?Z 利用图象平移正弦曲线 正弦、余弦函数的图象 1.3.2 正弦函数.余弦函数的图象和性质 正弦、余弦函数的图象 余弦函数的图象 正弦函数的图象 余弦曲线正弦曲线形状完全一样只是位置不同1.3.2 正弦函数.余弦函数的图象和性质与x轴的交点图象的最高点图象的最低点与x轴的交点图象的最高点图象的最低点(五点作图法)简图作法
(1) 列表(列出对图象形状起关键作用的五点坐标)(3) 连线(用光滑的曲线顺次连结五个点)(2) 描点(定出五个关键点)1.3.2 正弦函数.余弦函数的图象和性质列表(2)描点作图(2)y=sin2x , x∈[0,2π]2、五点作图法x0 1 0 -1 0Y1X0y=sin2x RR[?1,1][?1,1]ymax=1ymin= ?1ymax=1ymin= ?1定义域值 域最 值f(x)= 02?2?奇函数偶函数单调增区间:单调减区间:单调增区间:单调减区间:【例2】求下列函数的最大值,并求出最大值时x的集合:
(1)y=cos ,x?R ; (2) y=2-sin2x,x?R 解:(1)当cos =1,即x=6k? (k?Z)时,ymzx=1
∴函数的最大值为1,
取最大值时x的集合为{x|x=6k?,k?Z}.(2)当sin2x=-1时,即?x=k?- (k?Z)时,ymax=3 正弦、余弦函数的图象 正弦、余弦函数的图象 小
结1. 正弦曲线、余弦曲线y=sinx,x?[0, 2?]y=cosx,x?[0, 2?]1.3.2 正弦函数.余弦函数的图象和性质2.三角函数的基本性质 定义域、值域、周期性、奇偶性、单调性代数描点法(五点作图)几何描点法P46 2、3、4作业
将这些正弦线的终点连结起来AB1.3.2 正弦函数.余弦函数的图象和性质maths.gspy=sinx x?[0,2?]y=sinx x?R终边相同角的三角函数值相等 即: sin(x+2k?)=sinx, k?Z 利用图象平移正弦曲线 正弦、余弦函数的图象 1.3.2 正弦函数.余弦函数的图象和性质 正弦、余弦函数的图象 余弦函数的图象 正弦函数的图象 余弦曲线正弦曲线形状完全一样只是位置不同1.3.2 正弦函数.余弦函数的图象和性质与x轴的交点图象的最高点图象的最低点与x轴的交点图象的最高点图象的最低点(五点作图法)简图作法
(1) 列表(列出对图象形状起关键作用的五点坐标)(3) 连线(用光滑的曲线顺次连结五个点)(2) 描点(定出五个关键点)1.3.2 正弦函数.余弦函数的图象和性质列表(2)描点作图(2)y=sin2x , x∈[0,2π]2、五点作图法x0 1 0 -1 0Y1X0y=sin2x RR[?1,1][?1,1]ymax=1ymin= ?1ymax=1ymin= ?1定义域值 域最 值f(x)= 02?2?奇函数偶函数单调增区间:单调减区间:单调增区间:单调减区间:【例2】求下列函数的最大值,并求出最大值时x的集合:
(1)y=cos ,x?R ; (2) y=2-sin2x,x?R 解:(1)当cos =1,即x=6k? (k?Z)时,ymzx=1
∴函数的最大值为1,
取最大值时x的集合为{x|x=6k?,k?Z}.(2)当sin2x=-1时,即?x=k?- (k?Z)时,ymax=3 正弦、余弦函数的图象 正弦、余弦函数的图象 小
结1. 正弦曲线、余弦曲线y=sinx,x?[0, 2?]y=cosx,x?[0, 2?]1.3.2 正弦函数.余弦函数的图象和性质2.三角函数的基本性质 定义域、值域、周期性、奇偶性、单调性代数描点法(五点作图)几何描点法P46 2、3、4作业
