2014-2015学年度山东省滕州市实验中学高一第一学期期末考试数学试题
文档属性
| 名称 | 2014-2015学年度山东省滕州市实验中学高一第一学期期末考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 162.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-02-16 17:28:51 | ||
图片预览


文档简介
2014-2015学年度山东省滕州市实验中学高一第一学期期末考试
数学试题
第Ⅰ卷(共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项填涂到答题卡的相应位置.
1.已知集合,则集合=
A. B. C. D.
2.已知函数,则的值是
A.9 B. C. D.
3.下列函数中,既是奇函数又是增函数的为
A. B. C. D.
4.函数的定义域是
A. B. C. D.
5.下列函数中与函数是同一个函数的是
A. B. C. D.
6.若幂函数在上为增函数,则实数
A. B. C. D. 或
7.已知各顶点都在一个球面上的正方体的体积为,则这个球的表面积是
A. B. C. D.
8.设,用二分法求方程内近似解的过程中得,则方程的根落在区间
A. B. C. D.不能确定
9.在四面体中,两两垂直,且均相等,是的中点,则异面直线与所成的角为
A. B. C. D.
10.设,,则
A. B.
C. D.
11.一个几何体的三视图如图所示,则该几何体的体积是
A. B. C. D.
12.已知函数,则
A. B. C. D.
第Ⅱ卷(共90分)
二、填空题:本大题共4小题,每小题5分,共20分.请将答案填写到答题卡的相应位置.
13. .
14.函数的单调增区间是 .
15.已知函数的值域为,则 .
16.一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上.已知正三棱柱的底面边长为2,则该三角形的斜边长为 .
三、解答题:本大题共6小题,共70分. 解答应写出文字说明,证明过程或演算步骤,请将解答过程填写在答题卡的相应位置.
17.(10分)已知全集,,若,求的值.
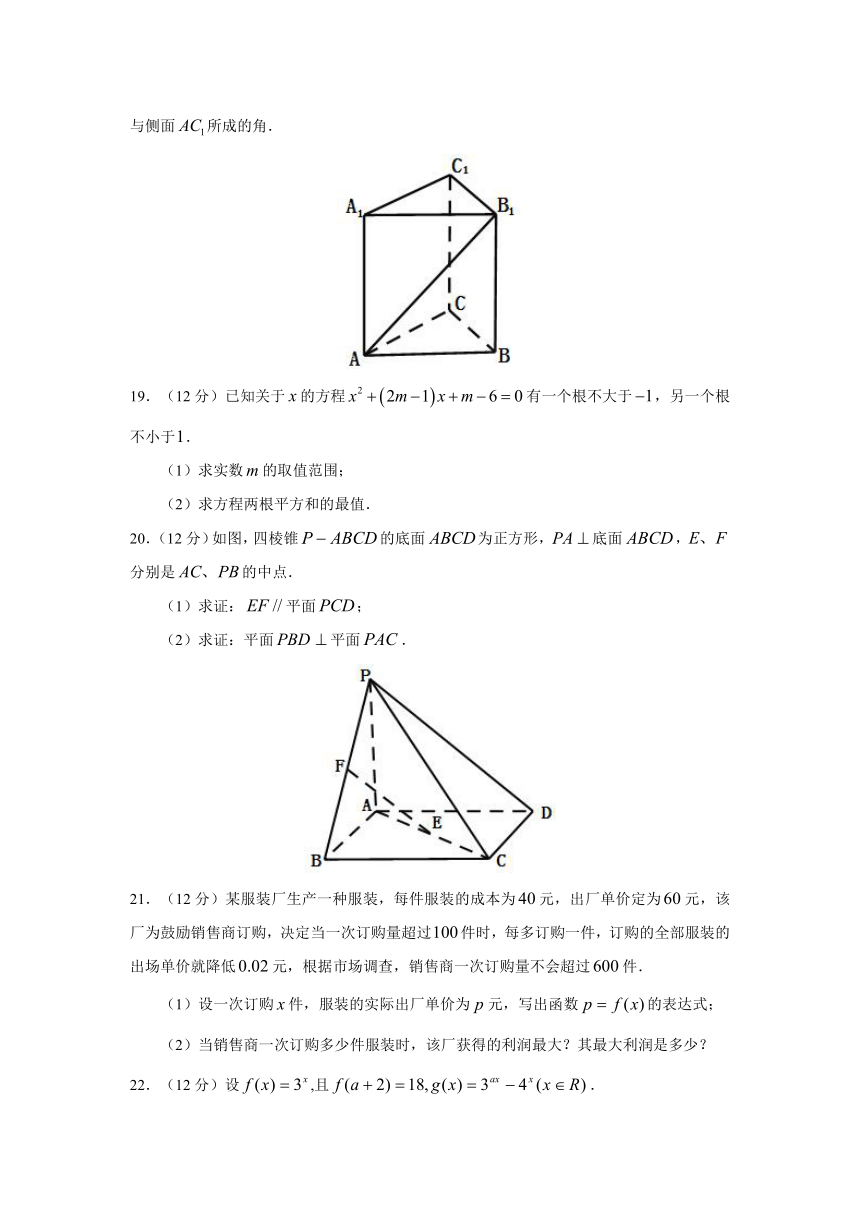
18.(12分)如图,在直三棱柱中,,,求与侧面所成的角.
19.(12分)已知关于的方程有一个根不大于,另一个根不小于.
(1)求实数的取值范围;
(2)求方程两根平方和的最值.
20.(12分)如图,四棱锥的底面为正方形,底面,分别是的中点.
(1)求证:平面;
(2)求证:平面平面.
21.(12分)某服装厂生产一种服装,每件服装的成本为元,出厂单价定为元,该厂为鼓励销售商订购,决定当一次订购量超过件时,每多订购一件,订购的全部服装的出场单价就降低元,根据市场调查,销售商一次订购量不会超过件.
(1)设一次订购件,服装的实际出厂单价为元,写出函数的表达式;
(2)当销售商一次订购多少件服装时,该厂获得的利润最大?其最大利润是多少?
22.(12分)设,且.
(1)求的解析式;
(2)判断在上的单调性并用定义证明;
(3)设,求集合.
2014-2015学年度山东省滕州市实验中学高一第一学期期末考试
数学试题参考答案
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
B
D
A
C
A
B
B
C
C
D
D
二、填空题:
13. 14. 15. 16.
解答题:
17.解:由,
得,
18.解:取的中点,连接,
∵ ∴,
∵ ∴ ∴,
∴是内的射影
∴是所成角
∵,
∴中,, ∴
∴所成角是.
19.解:(1)设,则,
解得:
(2)设方程的两根为,
则
∴
所以,当时。,当时。
20.解:(1)如图,连结,则是的中点,
又是的中点,∴.
又 ∵平面,面
∴平面.
(2) ∵ 是正方形,∴ ,
∵平面,∴ ,
又, ∴面.
又平面,
故平面平面.
21.解:(1)当时,;
当时,.
∴
(2)设利润为y元,则
当时,;
当时,.
∴
当时,是单调增函数,当时,最大,此时最大值为;
当时,,
∴当时,最大,此时,显然
所以当一次订购550件时,利润最大,最大利润为.
22.解:(1)∵,且
∴,
∵,∴
(2)上单调递减,证明如下:
设
∵ ∴∴
∴,∴
∴ ∴上单调递减
(3)方程为,令,则
方程在内有两个不同的解
由图知时,方程有两个不同解
∴
数学试题
第Ⅰ卷(共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项填涂到答题卡的相应位置.
1.已知集合,则集合=
A. B. C. D.
2.已知函数,则的值是
A.9 B. C. D.
3.下列函数中,既是奇函数又是增函数的为
A. B. C. D.
4.函数的定义域是
A. B. C. D.
5.下列函数中与函数是同一个函数的是
A. B. C. D.
6.若幂函数在上为增函数,则实数
A. B. C. D. 或
7.已知各顶点都在一个球面上的正方体的体积为,则这个球的表面积是
A. B. C. D.
8.设,用二分法求方程内近似解的过程中得,则方程的根落在区间
A. B. C. D.不能确定
9.在四面体中,两两垂直,且均相等,是的中点,则异面直线与所成的角为
A. B. C. D.
10.设,,则
A. B.
C. D.
11.一个几何体的三视图如图所示,则该几何体的体积是
A. B. C. D.
12.已知函数,则
A. B. C. D.
第Ⅱ卷(共90分)
二、填空题:本大题共4小题,每小题5分,共20分.请将答案填写到答题卡的相应位置.
13. .
14.函数的单调增区间是 .
15.已知函数的值域为,则 .
16.一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上.已知正三棱柱的底面边长为2,则该三角形的斜边长为 .
三、解答题:本大题共6小题,共70分. 解答应写出文字说明,证明过程或演算步骤,请将解答过程填写在答题卡的相应位置.
17.(10分)已知全集,,若,求的值.
18.(12分)如图,在直三棱柱中,,,求与侧面所成的角.
19.(12分)已知关于的方程有一个根不大于,另一个根不小于.
(1)求实数的取值范围;
(2)求方程两根平方和的最值.
20.(12分)如图,四棱锥的底面为正方形,底面,分别是的中点.
(1)求证:平面;
(2)求证:平面平面.
21.(12分)某服装厂生产一种服装,每件服装的成本为元,出厂单价定为元,该厂为鼓励销售商订购,决定当一次订购量超过件时,每多订购一件,订购的全部服装的出场单价就降低元,根据市场调查,销售商一次订购量不会超过件.
(1)设一次订购件,服装的实际出厂单价为元,写出函数的表达式;
(2)当销售商一次订购多少件服装时,该厂获得的利润最大?其最大利润是多少?
22.(12分)设,且.
(1)求的解析式;
(2)判断在上的单调性并用定义证明;
(3)设,求集合.
2014-2015学年度山东省滕州市实验中学高一第一学期期末考试
数学试题参考答案
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
B
D
A
C
A
B
B
C
C
D
D
二、填空题:
13. 14. 15. 16.
解答题:
17.解:由,
得,
18.解:取的中点,连接,
∵ ∴,
∵ ∴ ∴,
∴是内的射影
∴是所成角
∵,
∴中,, ∴
∴所成角是.
19.解:(1)设,则,
解得:
(2)设方程的两根为,
则
∴
所以,当时。,当时。
20.解:(1)如图,连结,则是的中点,
又是的中点,∴.
又 ∵平面,面
∴平面.
(2) ∵ 是正方形,∴ ,
∵平面,∴ ,
又, ∴面.
又平面,
故平面平面.
21.解:(1)当时,;
当时,.
∴
(2)设利润为y元,则
当时,;
当时,.
∴
当时,是单调增函数,当时,最大,此时最大值为;
当时,,
∴当时,最大,此时,显然
所以当一次订购550件时,利润最大,最大利润为.
22.解:(1)∵,且
∴,
∵,∴
(2)上单调递减,证明如下:
设
∵ ∴∴
∴,∴
∴ ∴上单调递减
(3)方程为,令,则
方程在内有两个不同的解
由图知时,方程有两个不同解
∴
同课章节目录
