北师大版九年级下册数学课件:3.9弧长及扇形的面积
文档属性
| 名称 | 北师大版九年级下册数学课件:3.9弧长及扇形的面积 |  | |
| 格式 | zip | ||
| 文件大小 | 866.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-04 09:51:30 | ||
图片预览





文档简介
课件21张PPT。9 弧长及扇形的面积1.经历探索弧长计算公式和扇形面积计算公式的过程,培养学生的探索能力.
2.了解弧长计算公式和扇形面积计算公式,并运用公式解决问题;训练学生的数学运用能力.1.已知⊙O的半径为R,⊙O的周长是多少?⊙O的面积是多少?2.什么叫圆心角?C=2πR,S=πR2. 角的顶点在圆心,角的两边分别与圆还有一个交点,这样的角叫做圆心角. 我们上体育课掷铅球练习时,要在指定的圆圈内进行,这个圆的直径是2.135m.这个圆的周长与面积是多少呢?(结果精确到0.01)周长约是6.71m,
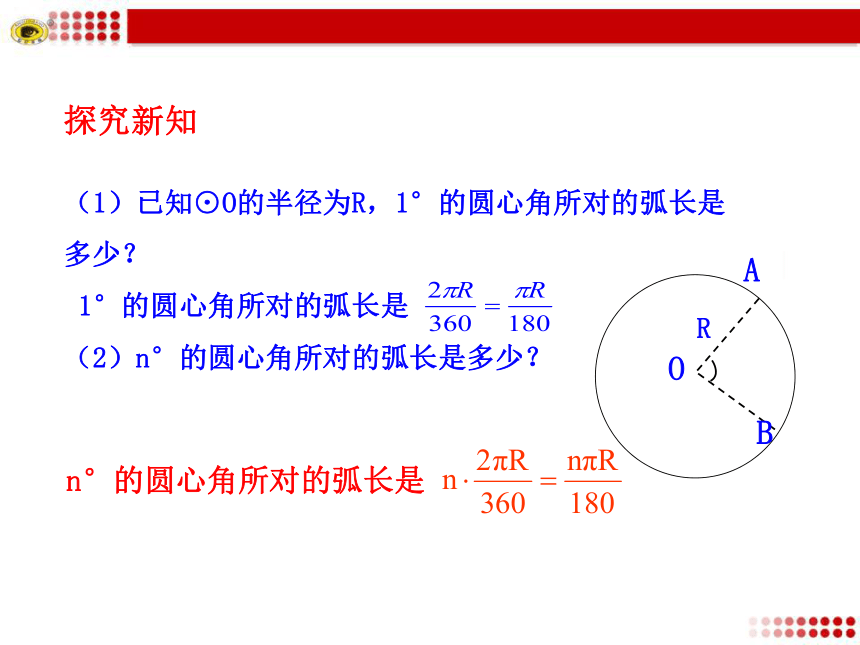
面积约是3.58㎡(1)已知⊙O的半径为R,1°的圆心角所对的弧长是
多少?
1°的圆心角所对的弧长是
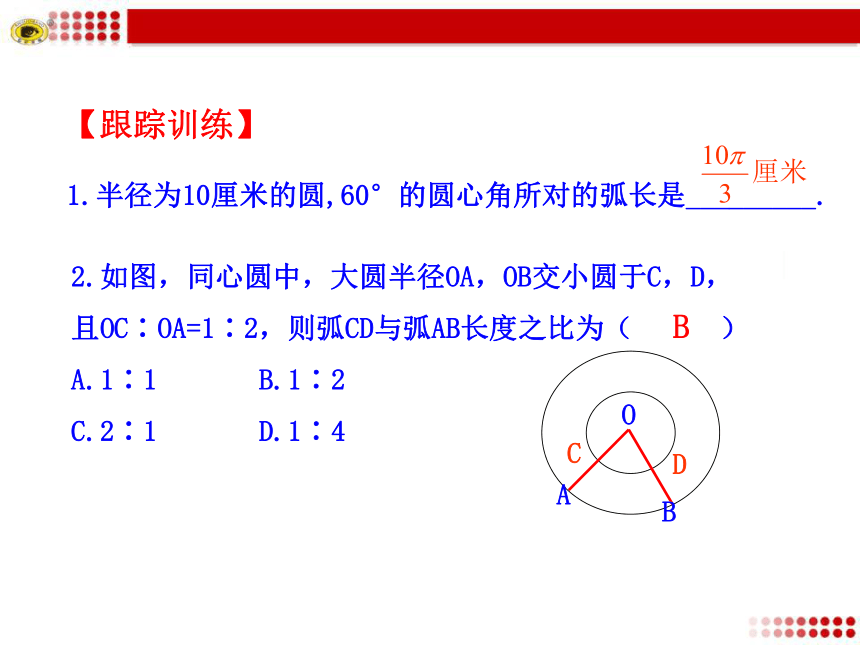
(2)n°的圆心角所对的弧长是多少?ABOR探究新知1.半径为10厘米的圆,60°的圆心角所对的弧长是_________.2.如图,同心圆中,大圆半径OA,OB交小圆于C,D,
且OC∶OA=1∶2,则弧CD与弧AB长度之比为( )
A.1∶1 B.1∶2
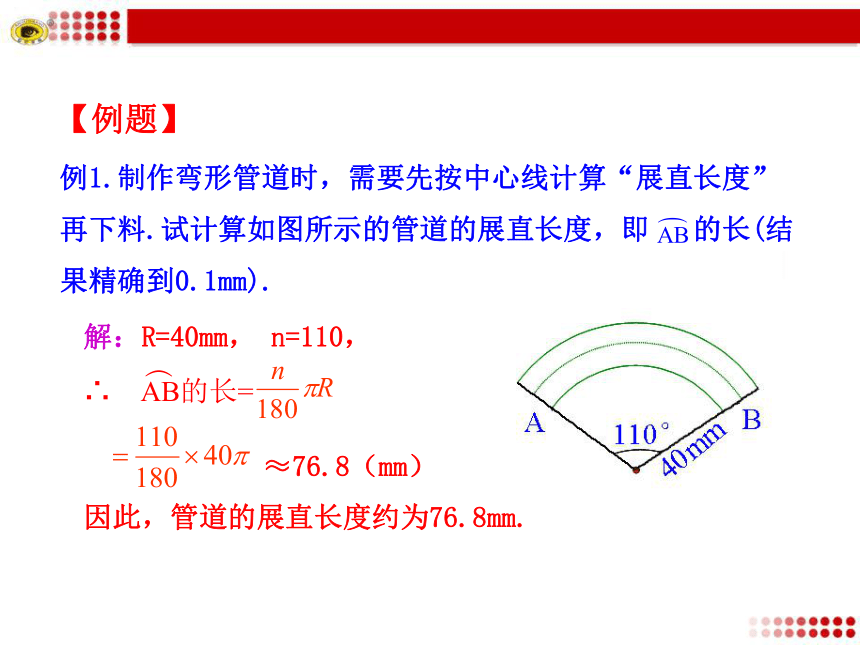
C.2∶1 D.1∶4OABCDB【跟踪训练】例1.制作弯形管道时,需要先按中心线计算“展直长度”再下料.试计算如图所示的管道的展直长度,即 的长(结果精确到0.1mm).解:R=40mm, n=110,≈76.8(mm)因此,管道的展直长度约为76.8mm.【例题】1.若圆的半径为R,60°的圆心角所对的弧长为l,则( )
A. l=R B. l于( )
A.24πcm B.12πcm
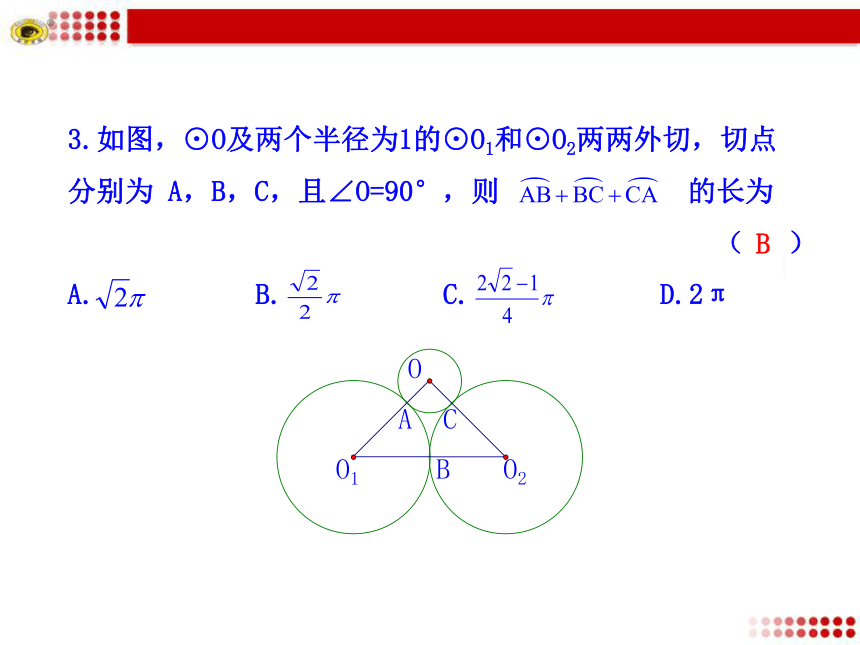
C.10πcm D.5πcmCC【跟踪训练】3.如图,⊙O及两个半径为1的⊙O1和⊙O2两两外切,切点
分别为 A,B,C,且∠O=90°,则 的长为
( )
A. B. C. D.2πB在一块空旷的草地上有一根柱子,柱子上栓着一条长3m的绳子,绳子的另一端拴着一只狗.
(1)这只狗的最大活动区域有多大?
(2)如果这只狗只能绕柱子转过n°角,那么它的最大活动区域有多大?探究新知 如果扇形的半径为R,圆心角为n°,那么扇形面积的计算公式为S扇形= .
比较扇形面积公式与弧长公式,你能用弧长来表示扇形的面积吗?
S扇形= l ,揭示新知例2.扇形AOB的半径为12cm,∠AOB= 120°,求 的长(结果精确到0.1cm)和扇形AOB的面积(结果精确到0.1cm2).解:≈25.1(cm).S扇形=≈150.8(cm2).【例题】1.一个扇形的圆心角为90o,半径为2,则弧长=_____,扇形面积=_______.
2.一个扇形的弧长为20πcm,面积是240πcm2,则该扇形的圆心角为_______.
3.已知扇形的圆心角为120°,半径为6,则扇形的弧长
是( )
A. 3π B.4π C.5π D.6πππ150oB【跟踪训练】4.如图的五个半圆,邻近的两个半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿
路线爬行,乙虫沿 路线爬行,则下列结
论正确的是( )
A.甲先到B点 B.乙先到B点
C.甲、乙同时到B点 D.无法确定答案:C1.(常德·中考)如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”. 则半径为2的“等边扇形”的面积为( )答案:CA.π B.1 C.2 D.2.(杭州·中考)如图,5个圆的圆心在同一条直线上, 且互相相切,若大圆直径是12,4个 小圆大小相等,则这5个圆的周长的和为( )
A.48π B.24π C.12π D.6π答案:B 答案:C 3.(聊城·中考)将一块三角板和半圆形量角器按
图中方式叠放,重叠部分(阴影)的量角器圆弧( )
对应的圆心角(∠AOB)为120o,AO的长为4cm,则图中
阴影部分的面积为( ) 4.(临沂·中考) 如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是( )
A.6π B.5π C.4π D.3π答案:A 【规律方法】在进行弧长或扇形面积计算时要注意下列问题:(1)公式中n表示1°的圆心角的倍数;(2)若圆心角的单位不全是度,则需先化为度后再计算.(3)题设没有标明精确度的,结果可以用π表示.1.弧长计算公式是什么?2.扇形的面积计算公式是什么?3.较复杂的图形的面积的计算可把它分解成几个特殊图形
的面积的和或差进行计算.凡没有就着泪水吃过面包的人是不懂得人生之味的人。
——歌德
2.了解弧长计算公式和扇形面积计算公式,并运用公式解决问题;训练学生的数学运用能力.1.已知⊙O的半径为R,⊙O的周长是多少?⊙O的面积是多少?2.什么叫圆心角?C=2πR,S=πR2. 角的顶点在圆心,角的两边分别与圆还有一个交点,这样的角叫做圆心角. 我们上体育课掷铅球练习时,要在指定的圆圈内进行,这个圆的直径是2.135m.这个圆的周长与面积是多少呢?(结果精确到0.01)周长约是6.71m,
面积约是3.58㎡(1)已知⊙O的半径为R,1°的圆心角所对的弧长是
多少?
1°的圆心角所对的弧长是
(2)n°的圆心角所对的弧长是多少?ABOR探究新知1.半径为10厘米的圆,60°的圆心角所对的弧长是_________.2.如图,同心圆中,大圆半径OA,OB交小圆于C,D,
且OC∶OA=1∶2,则弧CD与弧AB长度之比为( )
A.1∶1 B.1∶2
C.2∶1 D.1∶4OABCDB【跟踪训练】例1.制作弯形管道时,需要先按中心线计算“展直长度”再下料.试计算如图所示的管道的展直长度,即 的长(结果精确到0.1mm).解:R=40mm, n=110,≈76.8(mm)因此,管道的展直长度约为76.8mm.【例题】1.若圆的半径为R,60°的圆心角所对的弧长为l,则( )
A. l=R B. l
A.24πcm B.12πcm
C.10πcm D.5πcmCC【跟踪训练】3.如图,⊙O及两个半径为1的⊙O1和⊙O2两两外切,切点
分别为 A,B,C,且∠O=90°,则 的长为
( )
A. B. C. D.2πB在一块空旷的草地上有一根柱子,柱子上栓着一条长3m的绳子,绳子的另一端拴着一只狗.
(1)这只狗的最大活动区域有多大?
(2)如果这只狗只能绕柱子转过n°角,那么它的最大活动区域有多大?探究新知 如果扇形的半径为R,圆心角为n°,那么扇形面积的计算公式为S扇形= .
比较扇形面积公式与弧长公式,你能用弧长来表示扇形的面积吗?
S扇形= l ,揭示新知例2.扇形AOB的半径为12cm,∠AOB= 120°,求 的长(结果精确到0.1cm)和扇形AOB的面积(结果精确到0.1cm2).解:≈25.1(cm).S扇形=≈150.8(cm2).【例题】1.一个扇形的圆心角为90o,半径为2,则弧长=_____,扇形面积=_______.
2.一个扇形的弧长为20πcm,面积是240πcm2,则该扇形的圆心角为_______.
3.已知扇形的圆心角为120°,半径为6,则扇形的弧长
是( )
A. 3π B.4π C.5π D.6πππ150oB【跟踪训练】4.如图的五个半圆,邻近的两个半圆相切,两只小虫同时出发,以相同的速度从A点到B点,甲虫沿
路线爬行,乙虫沿 路线爬行,则下列结
论正确的是( )
A.甲先到B点 B.乙先到B点
C.甲、乙同时到B点 D.无法确定答案:C1.(常德·中考)如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”. 则半径为2的“等边扇形”的面积为( )答案:CA.π B.1 C.2 D.2.(杭州·中考)如图,5个圆的圆心在同一条直线上, 且互相相切,若大圆直径是12,4个 小圆大小相等,则这5个圆的周长的和为( )
A.48π B.24π C.12π D.6π答案:B 答案:C 3.(聊城·中考)将一块三角板和半圆形量角器按
图中方式叠放,重叠部分(阴影)的量角器圆弧( )
对应的圆心角(∠AOB)为120o,AO的长为4cm,则图中
阴影部分的面积为( ) 4.(临沂·中考) 如图,直径AB为6的半圆,绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是( )
A.6π B.5π C.4π D.3π答案:A 【规律方法】在进行弧长或扇形面积计算时要注意下列问题:(1)公式中n表示1°的圆心角的倍数;(2)若圆心角的单位不全是度,则需先化为度后再计算.(3)题设没有标明精确度的,结果可以用π表示.1.弧长计算公式是什么?2.扇形的面积计算公式是什么?3.较复杂的图形的面积的计算可把它分解成几个特殊图形
的面积的和或差进行计算.凡没有就着泪水吃过面包的人是不懂得人生之味的人。
——歌德
