2015高考数学二轮复习:直线与圆
图片预览



文档简介
2015高考数学二轮复习:直线与圆
直线方程:
直线名称 已知条件 直线方程 使用范围
点斜式 存在
斜截式 存在
两点式
截距式
一般式
1.倾斜角定义: 取值范围: 斜率定义: =
2.平面两点距离: ,空间两点距离:
3.点到直线的距离为:
4.两平行线之间的距离:
1.写出下列直线的方程
(1)倾斜角为,在轴上的截距为
(2)在轴上的截距为 ,在轴上的截距为
(3)经过点,倾斜角为
(4)经过两点
(5)经过点,且在两坐标轴截距相等
2.求过点,且与直线平行的直线方程
3.求过点,且与直线垂直的直线方程
4.直线过点,且斜率是直线斜率的四倍,则方程为
5.直线过点,且倾斜角是直线倾斜角的四倍,则方程为
6.直线过点,且倾斜角是直线倾斜角的两倍,则方程为
7.直线恒过定点坐标为
8.当= 时,两直线和平行
9.已知点是直线与轴的交点,求把直线绕点逆时针方向旋转得到的直线方程
10.求与直线平行,且在两坐标轴上的截距之和为的直线的方程
11.求点到直线距离:
(1) (2) (3)
12.两平行线:,:的距离
13.空间两点间的距离是
14.在坐标平面上,不等式组所表示的平面区域的面积是
15.设满足约束条件
(1)求的取值范围
(2)求的取值范围
(3)求的取值范围
2015高考数学专题复习:直线与圆
一、定义:
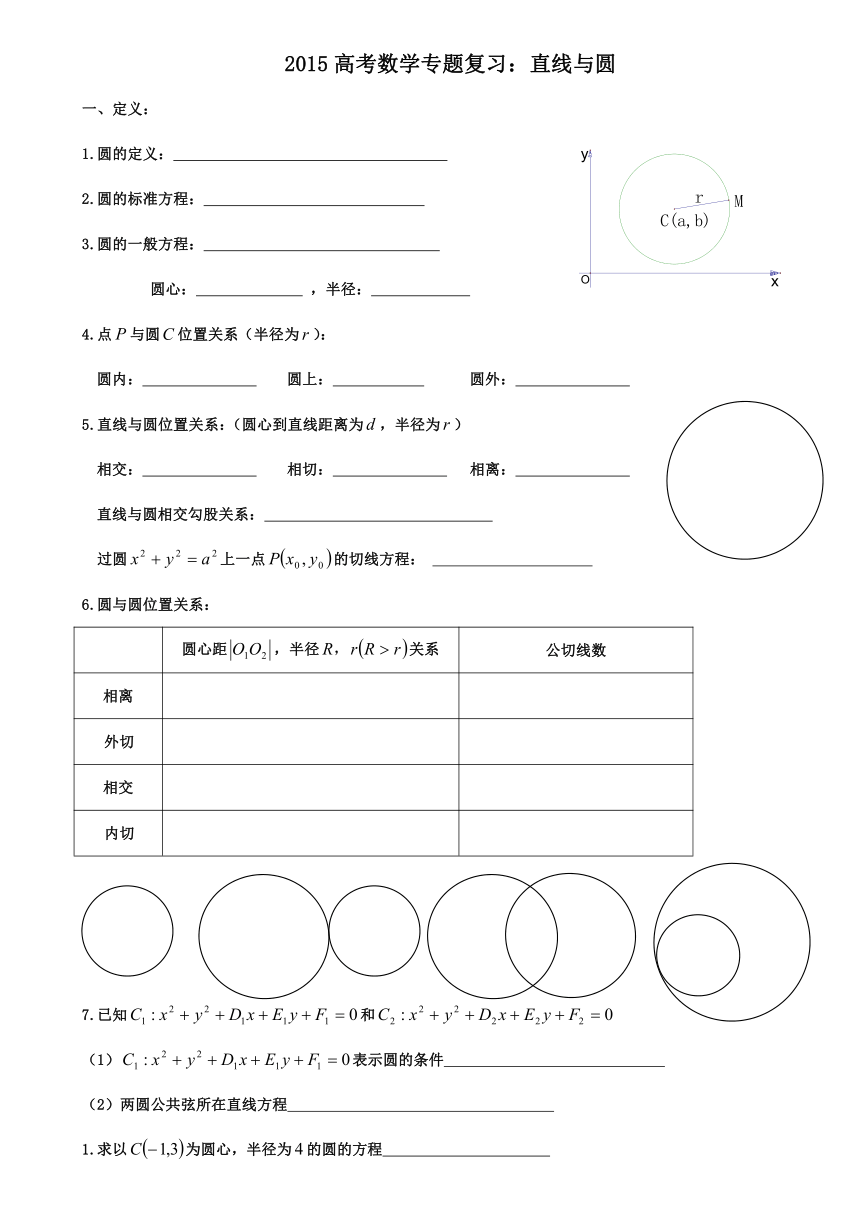
1.圆的定义:
2.圆的标准方程:
3.圆的一般方程:
圆心: ,半径:
4.点与圆位置关系(半径为):
圆内: 圆上: 圆外:
5.直线与圆位置关系:(圆心到直线距离为,半径为)
相交: 相切: 相离:
直线与圆相交勾股关系:
过圆上一点的切线方程:
6.圆与圆位置关系:
圆心距,半径关系 公切线数
相离
外切
相交
内切
7.已知和
(1)表示圆的条件
(2)两圆公共弦所在直线方程
1.求以为圆心,半径为的圆的方程
2.求圆和的圆心及半径
3.(2012山东) 圆与圆的位置关系为 ( )
A.内切 B.相交 C.外切 D.相离
4.求圆心为且与直线相切的圆的方程
5.若过两点、的直线与圆相切,则
6.若直线与圆切于点,则=
7.直线被曲线所截得的弦长
8.(1)过点作圆的切线, 求切线方程:
(2)过圆上一点的切线方程:
9.过的直线截圆所得弦长为,求直线方程:
10.求圆心在轴上,且过两点的圆的方程
11.直线经过坐标原点,且与圆相切,切点在第四象限,则直线的方程为
12.直线与圆,求上各点到的距离的最小值
13.圆上的点到直线的最大距离
14.由直线上的一点向圆引切线,求切线长的最小值
15.一束光线从点出发经轴反射到圆上的最短路程
16.已知,求的取值范围
17.若直线与圆相交于两点,且,则
18.已知直线与圆相交于两点,且,则
19.直线与圆交于两点,则
20(13山东)过点作圆的两条切线,切点分别为,则直线的方程为 ( )
A. B. C. D.
21(10山东理)已知圆过点,且圆心在轴的正半轴上,直线:被圆所截得的弦长为,则过圆心且与直线垂直的直线的方程为 .
22(13山东文)过点作圆的弦,其中最短的弦长为__________
23(08山东)若圆的半径为1,圆心在第一象限,且与直线和轴相切,则该圆的标准方程是( )
A. B. C. D.
24.已知三角形三个顶点坐标,求外接圆方程
1.
2.
25.已知圆经过坐标原点,且与直线相切,切点为
(1)求圆的方程
(2)若斜率为的直线与圆相交于不同的两点,求的取值范围
26.为坐标原点,曲线上有两点关于直线对称,且
(1)求的值
(2)求直线的方程
27.已知为坐标原点,圆与直线交于两点,且
,求的值
2015高考数学专题复习:直线与圆测试题
一、选择题:
1.已知圆,过点,则 ( )
A.与相交 B.与相切 C.与相离 D.以上三个选项均有可能
2.当直线:被截得弦长为时,则= ( )
A. B. C. D.
3.圆截轴所得的弦与截轴所得的弦的长度之比为 ( )
A. B. C. D.
4.圆的圆心到直线的距离是 ( )
A. B. C. D.
5.过点且圆心在直线上的圆的方程是 ( )
A. B.
C. D.
6.设直线过点,其斜率为,且与圆相切,则的值为 ( )
A. B. C. D.
7.圆和圆的位置关系是 ( )
A.相离 B.相交 C.外切 D.内切
8.直线平分圆,则的最小值是 ( )
A. B. C. D.
9.若直线与直线互相垂直,那么的值等于 ( )
A.1 B. C. D.
10.直线与圆相切,则实数等于 ( )
A.或 B.或 C.或 D.或
二、填空题:
11.已知,直线过点,求点到的距离的最大值__________
12.直线必过点
13.已知点在曲线上,则的取值范围是
14.已知圆的方程为设该圆中过点的最长弦和最短弦分别为和,
则四边形的面积是
15.过点作圆的两条切线,切点分别为,直线的方程为
三.解答题
16.已知的顶点,求:
(1)边上的高所在直线的方程
(2)边上的中线所在直线的方程
(3)外接圆方程
17.过的直线截圆所得弦长为,求直线方程
18.已知圆的半径为,圆心在直线上,圆被直线截得的弦长为,求圆的标准方程
19.已知关于的方程.
(1)方程表示圆时的取值范围
(2)若圆与直线相交于两点,且=,求的值
20.已知圆经过两点,且在轴上截得的线段长为,半径小于
(1)求直线与圆的方程
(2)若直线,且与圆交于点,,求直线的方程
21.已知以点为圆心的圆过点,线段的垂直平分线交圆于点,且
求直线的方程
求圆的方程
设点在圆上,试探究使面积为的点共有几个?并证明结论
2015高考数学专题复习:对称问题
对称问题可以分为:点关于点的对称,线关于点的对称,点关于线的对称,线关于线对称,圆关于线对称
一.点关于点的对称问题
1.求点关于点对称的点的坐标
二.直线关于点对称的问题
2.求直线关于点对称的直线方程
三.点关于直线的对称问题
3.求点关于直线的对称点的坐标
四.直线关于直线的对称问题
4.求直线关于直线对称的直线的方程
5.求直线关于直线的对称直线的方程
五.圆关于线对称:
6.圆关于直线对称的圆的方程
练习:
7.点关于点对称的点的坐标
8.已知点与点关于轴对称,点与点关于轴对称,点与点关于直线对称,
则点的坐标为
9.求直线关于点对称直线的方程
10.点关于直线的对称点为,则的方程
11.求直线关于直线 的轴对称直线的方程
12.求圆关于直线对称的圆的方程
13.求圆关于直线对称的圆的方程
14.已知圆的圆心与点关于直线对称.直线与圆相交于两点,
且,求圆的方程
15.一束光线通过点,经直线反射,如果反射光线通过点,求反射
光线所在直线的方程
16.直线上有一点,它与两定点的距离之和最小值为 ,此时点的坐标为
17.直线上有一点,它与两定点的距离之差最大值为 ,此时点的
坐标为
18.已知的顶点为,边上的中线所在直线方程为,的平分线所在
直线方程为,求边所在直线的方程
2015高考数学专题复习:直线与圆测试题
1.已知点是圆上的定点,经过点的直线与该圆交于另一点,当
面积最大时,直线的方程是_______
2.已知圆上有且只有四个点到直线的距离为,则实数的取值范围是________
3.已知两点,经过,且与轴相切的圆有且只有一个,求的值及圆的方程
4.已知圆和圆外一点
(1)过作直线与圆交于两点,若,求直线的方程
(2)过作圆的切线,切点为,求切线长及所在直线的方程.
5.若直线与圆相切,求的取值范围
6.已知是直线上的动点,是圆的切线,是切点,
是圆心,求四边形面积的最小值
7.直线,恒过定点
8.已知点是直线与轴的交点,求把直线绕点逆时针方向旋转得到的直线
方程
9.直线与曲线有且仅有一个公共点,则的取值范围是 ( )
A. B.或 C. D.
10.已知圆,直线
(1)求证:对,直线与圆总有两个不同的交点
(2)设与圆交于两点,若,求的倾斜角
(3)求直线中,截圆所得的弦最长及最短时的直线方程.
11.若直线与曲线有公共点,求的取值范围
12.若圆关于直线对称,求由点向圆所作的切线长的最小值
13.两圆和恰有三条公切线,,求
的最小值
14.圆被轴所截得弦为,若弦所对圆心角为,实数
15.求与已知圆相交所得公共弦平行于直线且过点
的圆的方程
16.已知正方形的相对顶点,求顶点和的坐标
17.为何值时,直线与曲线有两个公共点?有一个公共点?
18.直线与圆相交于两点,若,则的取值范围是
19.若直线与曲线有两个不同的公共点,求实数的取值范围
20.已知圆的半径为,圆心在直线上,圆被直线截得的弦长为,求圆的标准方程
点为圆的弦的中点,求该弦所在直线的方程
22.将一张坐标纸折叠一次,使点与重合,则与点重合的点是
23.若直线与圆的两个交点关于直线对称,则 .
24.直线与圆相交于两点(其中是实数),且是直角三角形,
则点与点之间距离的最小值为
25.已知点,若点是圆上的动点,则面积的最小值为 .
26.已知圆,圆的圆心在直线上,且与的两个交点平分,
求满足条件圆半径的最小值
.
直线方程:
直线名称 已知条件 直线方程 使用范围
点斜式 存在
斜截式 存在
两点式
截距式
一般式
1.倾斜角定义: 取值范围: 斜率定义: =
2.平面两点距离: ,空间两点距离:
3.点到直线的距离为:
4.两平行线之间的距离:
1.写出下列直线的方程
(1)倾斜角为,在轴上的截距为
(2)在轴上的截距为 ,在轴上的截距为
(3)经过点,倾斜角为
(4)经过两点
(5)经过点,且在两坐标轴截距相等
2.求过点,且与直线平行的直线方程
3.求过点,且与直线垂直的直线方程
4.直线过点,且斜率是直线斜率的四倍,则方程为
5.直线过点,且倾斜角是直线倾斜角的四倍,则方程为
6.直线过点,且倾斜角是直线倾斜角的两倍,则方程为
7.直线恒过定点坐标为
8.当= 时,两直线和平行
9.已知点是直线与轴的交点,求把直线绕点逆时针方向旋转得到的直线方程
10.求与直线平行,且在两坐标轴上的截距之和为的直线的方程
11.求点到直线距离:
(1) (2) (3)
12.两平行线:,:的距离
13.空间两点间的距离是
14.在坐标平面上,不等式组所表示的平面区域的面积是
15.设满足约束条件
(1)求的取值范围
(2)求的取值范围
(3)求的取值范围
2015高考数学专题复习:直线与圆
一、定义:
1.圆的定义:
2.圆的标准方程:
3.圆的一般方程:
圆心: ,半径:
4.点与圆位置关系(半径为):
圆内: 圆上: 圆外:
5.直线与圆位置关系:(圆心到直线距离为,半径为)
相交: 相切: 相离:
直线与圆相交勾股关系:
过圆上一点的切线方程:
6.圆与圆位置关系:
圆心距,半径关系 公切线数
相离
外切
相交
内切
7.已知和
(1)表示圆的条件
(2)两圆公共弦所在直线方程
1.求以为圆心,半径为的圆的方程
2.求圆和的圆心及半径
3.(2012山东) 圆与圆的位置关系为 ( )
A.内切 B.相交 C.外切 D.相离
4.求圆心为且与直线相切的圆的方程
5.若过两点、的直线与圆相切,则
6.若直线与圆切于点,则=
7.直线被曲线所截得的弦长
8.(1)过点作圆的切线, 求切线方程:
(2)过圆上一点的切线方程:
9.过的直线截圆所得弦长为,求直线方程:
10.求圆心在轴上,且过两点的圆的方程
11.直线经过坐标原点,且与圆相切,切点在第四象限,则直线的方程为
12.直线与圆,求上各点到的距离的最小值
13.圆上的点到直线的最大距离
14.由直线上的一点向圆引切线,求切线长的最小值
15.一束光线从点出发经轴反射到圆上的最短路程
16.已知,求的取值范围
17.若直线与圆相交于两点,且,则
18.已知直线与圆相交于两点,且,则
19.直线与圆交于两点,则
20(13山东)过点作圆的两条切线,切点分别为,则直线的方程为 ( )
A. B. C. D.
21(10山东理)已知圆过点,且圆心在轴的正半轴上,直线:被圆所截得的弦长为,则过圆心且与直线垂直的直线的方程为 .
22(13山东文)过点作圆的弦,其中最短的弦长为__________
23(08山东)若圆的半径为1,圆心在第一象限,且与直线和轴相切,则该圆的标准方程是( )
A. B. C. D.
24.已知三角形三个顶点坐标,求外接圆方程
1.
2.
25.已知圆经过坐标原点,且与直线相切,切点为
(1)求圆的方程
(2)若斜率为的直线与圆相交于不同的两点,求的取值范围
26.为坐标原点,曲线上有两点关于直线对称,且
(1)求的值
(2)求直线的方程
27.已知为坐标原点,圆与直线交于两点,且
,求的值
2015高考数学专题复习:直线与圆测试题
一、选择题:
1.已知圆,过点,则 ( )
A.与相交 B.与相切 C.与相离 D.以上三个选项均有可能
2.当直线:被截得弦长为时,则= ( )
A. B. C. D.
3.圆截轴所得的弦与截轴所得的弦的长度之比为 ( )
A. B. C. D.
4.圆的圆心到直线的距离是 ( )
A. B. C. D.
5.过点且圆心在直线上的圆的方程是 ( )
A. B.
C. D.
6.设直线过点,其斜率为,且与圆相切,则的值为 ( )
A. B. C. D.
7.圆和圆的位置关系是 ( )
A.相离 B.相交 C.外切 D.内切
8.直线平分圆,则的最小值是 ( )
A. B. C. D.
9.若直线与直线互相垂直,那么的值等于 ( )
A.1 B. C. D.
10.直线与圆相切,则实数等于 ( )
A.或 B.或 C.或 D.或
二、填空题:
11.已知,直线过点,求点到的距离的最大值__________
12.直线必过点
13.已知点在曲线上,则的取值范围是
14.已知圆的方程为设该圆中过点的最长弦和最短弦分别为和,
则四边形的面积是
15.过点作圆的两条切线,切点分别为,直线的方程为
三.解答题
16.已知的顶点,求:
(1)边上的高所在直线的方程
(2)边上的中线所在直线的方程
(3)外接圆方程
17.过的直线截圆所得弦长为,求直线方程
18.已知圆的半径为,圆心在直线上,圆被直线截得的弦长为,求圆的标准方程
19.已知关于的方程.
(1)方程表示圆时的取值范围
(2)若圆与直线相交于两点,且=,求的值
20.已知圆经过两点,且在轴上截得的线段长为,半径小于
(1)求直线与圆的方程
(2)若直线,且与圆交于点,,求直线的方程
21.已知以点为圆心的圆过点,线段的垂直平分线交圆于点,且
求直线的方程
求圆的方程
设点在圆上,试探究使面积为的点共有几个?并证明结论
2015高考数学专题复习:对称问题
对称问题可以分为:点关于点的对称,线关于点的对称,点关于线的对称,线关于线对称,圆关于线对称
一.点关于点的对称问题
1.求点关于点对称的点的坐标
二.直线关于点对称的问题
2.求直线关于点对称的直线方程
三.点关于直线的对称问题
3.求点关于直线的对称点的坐标
四.直线关于直线的对称问题
4.求直线关于直线对称的直线的方程
5.求直线关于直线的对称直线的方程
五.圆关于线对称:
6.圆关于直线对称的圆的方程
练习:
7.点关于点对称的点的坐标
8.已知点与点关于轴对称,点与点关于轴对称,点与点关于直线对称,
则点的坐标为
9.求直线关于点对称直线的方程
10.点关于直线的对称点为,则的方程
11.求直线关于直线 的轴对称直线的方程
12.求圆关于直线对称的圆的方程
13.求圆关于直线对称的圆的方程
14.已知圆的圆心与点关于直线对称.直线与圆相交于两点,
且,求圆的方程
15.一束光线通过点,经直线反射,如果反射光线通过点,求反射
光线所在直线的方程
16.直线上有一点,它与两定点的距离之和最小值为 ,此时点的坐标为
17.直线上有一点,它与两定点的距离之差最大值为 ,此时点的
坐标为
18.已知的顶点为,边上的中线所在直线方程为,的平分线所在
直线方程为,求边所在直线的方程
2015高考数学专题复习:直线与圆测试题
1.已知点是圆上的定点,经过点的直线与该圆交于另一点,当
面积最大时,直线的方程是_______
2.已知圆上有且只有四个点到直线的距离为,则实数的取值范围是________
3.已知两点,经过,且与轴相切的圆有且只有一个,求的值及圆的方程
4.已知圆和圆外一点
(1)过作直线与圆交于两点,若,求直线的方程
(2)过作圆的切线,切点为,求切线长及所在直线的方程.
5.若直线与圆相切,求的取值范围
6.已知是直线上的动点,是圆的切线,是切点,
是圆心,求四边形面积的最小值
7.直线,恒过定点
8.已知点是直线与轴的交点,求把直线绕点逆时针方向旋转得到的直线
方程
9.直线与曲线有且仅有一个公共点,则的取值范围是 ( )
A. B.或 C. D.
10.已知圆,直线
(1)求证:对,直线与圆总有两个不同的交点
(2)设与圆交于两点,若,求的倾斜角
(3)求直线中,截圆所得的弦最长及最短时的直线方程.
11.若直线与曲线有公共点,求的取值范围
12.若圆关于直线对称,求由点向圆所作的切线长的最小值
13.两圆和恰有三条公切线,,求
的最小值
14.圆被轴所截得弦为,若弦所对圆心角为,实数
15.求与已知圆相交所得公共弦平行于直线且过点
的圆的方程
16.已知正方形的相对顶点,求顶点和的坐标
17.为何值时,直线与曲线有两个公共点?有一个公共点?
18.直线与圆相交于两点,若,则的取值范围是
19.若直线与曲线有两个不同的公共点,求实数的取值范围
20.已知圆的半径为,圆心在直线上,圆被直线截得的弦长为,求圆的标准方程
点为圆的弦的中点,求该弦所在直线的方程
22.将一张坐标纸折叠一次,使点与重合,则与点重合的点是
23.若直线与圆的两个交点关于直线对称,则 .
24.直线与圆相交于两点(其中是实数),且是直角三角形,
则点与点之间距离的最小值为
25.已知点,若点是圆上的动点,则面积的最小值为 .
26.已知圆,圆的圆心在直线上,且与的两个交点平分,
求满足条件圆半径的最小值
.
同课章节目录
