2024北师大版数学九年级下学期课时练--专项素养综合全练(十)跨学科试题(含解析)
文档属性
| 名称 | 2024北师大版数学九年级下学期课时练--专项素养综合全练(十)跨学科试题(含解析) | 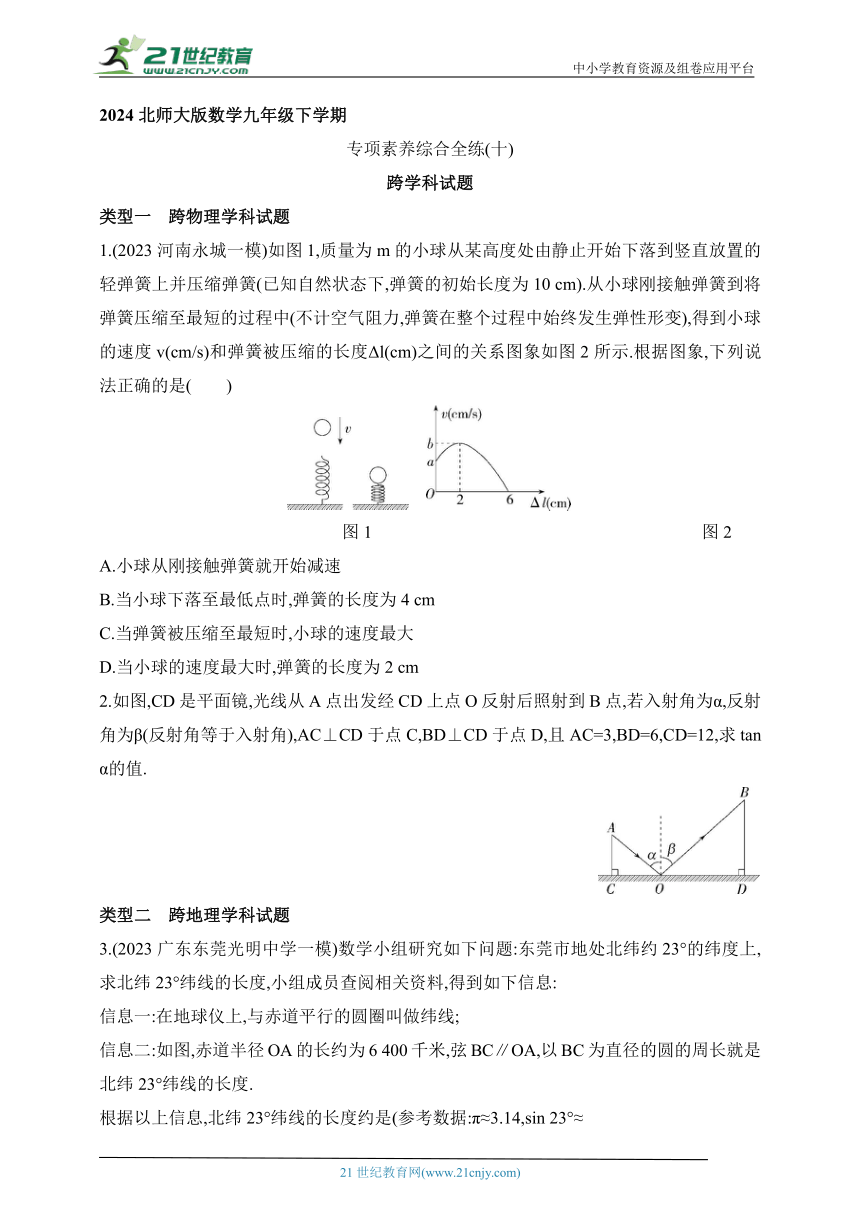 | |
| 格式 | docx | ||
| 文件大小 | 392.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 13:01:20 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024北师大版数学九年级下学期
专项素养综合全练(十)
跨学科试题
类型一 跨物理学科试题
1.(2023河南永城一模)如图1,质量为m的小球从某高度处由静止开始下落到竖直放置的轻弹簧上并压缩弹簧(已知自然状态下,弹簧的初始长度为10 cm).从小球刚接触弹簧到将弹簧压缩至最短的过程中(不计空气阻力,弹簧在整个过程中始终发生弹性形变),得到小球的速度v(cm/s)和弹簧被压缩的长度Δl(cm)之间的关系图象如图2所示.根据图象,下列说法正确的是( )
图1 图2
A.小球从刚接触弹簧就开始减速
B.当小球下落至最低点时,弹簧的长度为4 cm
C.当弹簧被压缩至最短时,小球的速度最大
D.当小球的速度最大时,弹簧的长度为2 cm
2.如图,CD是平面镜,光线从A点出发经CD上点O反射后照射到B点,若入射角为α,反射角为β(反射角等于入射角),AC⊥CD于点C,BD⊥CD于点D,且AC=3,BD=6,CD=12,求tan α的值.
类型二 跨地理学科试题
3.(2023广东东莞光明中学一模)数学小组研究如下问题:东莞市地处北纬约23°的纬度上,求北纬23°纬线的长度,小组成员查阅相关资料,得到如下信息:
信息一:在地球仪上,与赤道平行的圆圈叫做纬线;
信息二:如图,赤道半径OA的长约为6 400千米,弦BC∥OA,以BC为直径的圆的周长就是北纬23°纬线的长度.
根据以上信息,北纬23°纬线的长度约是(参考数据:π≈3.14,sin 23°≈
0.39,cos 23°≈0.92,tan 23°≈0.42)( )
A.5 900千米 B.16 000千米 C.37 000千米 D.42 000千米
4.【国防科技】(2023湖北宜昌中考)2023年5月30日,“神舟十六号”航天飞船成功发射.飞船在离地球大约330 km的圆形轨道上,如图,当运行到地球表面P点的正上方F点时,从中直接看到地球表面一个最远的点是点Q.在Rt△OQF中,OP=OQ≈6 400 km.
(参考数据:cos 16°≈0.96,cos 18°≈0.95,cos 20°≈0.94,cos 22°≈0.93,π≈3.14)
(1)求cos α的值(精确到0.01);
(2)在☉O中,求的长(结果取整数).
类型三 跨语文学科试题
5.(2021湖南湘西州中考)有诗云:东山雨霁画屏开,风卷松声入耳来.一座楼阁镇四方,团结一心建家乡.1987年为庆祝湘西自治州成立三十周年,湘西州政府在花果山公园内修建了一座三层楼高的“一心阁”民族团结楼阁.如图,某学校数学实践活动小组为测量“一心阁”CH的高度,在楼前的平地上A处,观测到楼顶C处的仰角为30°,在平地上B处观测到楼顶C处的仰角为45°,并测得A、B两处相距20 m,求“一心阁”CH的高度.(结果保留小数点后一位,参考数据:≈1.41,≈1.73)
类型四 跨历史学科试题
6.(2023浙江宁波外国语学校三模)如图1,耸立在宁波海曙区的天封塔始建于唐武则天“天册万岁”至“万岁登封”(695—696)年间,因建塔年号始末“天”“封”而得名.如图2,在天封塔正前方有一斜坡CD,长为13米,坡度为1∶2.4,高为DE.某中学数学兴趣小组的同学利用测角仪在斜坡底的点C处测得塔上观景点P的仰角为64°,在斜坡顶的点D处测得塔上观景点P的仰角为45°(其中点A,C,E在同一直线上).
(1)求斜坡的高DE;
(2)求塔上观景点P距离地面的高度.(结果精确到1米,参考数据:
sin 64°≈0.9,tan 64°≈2)
图1 图2
答案全解全析
1.B 由图象可知,弹簧被压缩2 cm后小球开始减速,故选项A不合题意;由图象可知,当小球下落至最低点时,弹簧被压缩的长度为6 cm,此时弹簧的长度为10-6=4(cm),故选项B符合题意;由图象可知,当弹簧被压缩至最短时,小球的速度最小,为0 cm/s,故选项C不合题意;由图象可知,小球速度最大时,弹簧被压缩2 cm,此时弹簧的长度为10-2=
8 cm,故选项D不合题意.故选B.
2.解析 如图,由题意得OP⊥CD,∵AC⊥CD,∴AC∥OP,∴∠A=α,同理可得∠B=β,∵α=β,∴∠A=∠B,又∵∠ACO=∠BDO=90°,∴△AOC∽△BOD,∴
,解得OC=4,∴tan α=tan A=.
3.C 作OH⊥BC于H,∴BH=CH=BC,
∵OA∥BC,∴∠B=∠AOB=23°,∴cos B=cos 23°=,
∵OB=OA=6 400千米,∴BH≈6 400×0.92=5 888(千米),
∴BC=2BH=11 776(千米),
∴以BC为直径的圆的周长=π×11 776≈3.14×11 776=36 976.64≈
37 000(千米).
∴北纬23°纬线的长度约是37 000千米.故选C.
4.解析 (1)由题意知FQ是☉O的切线,
∴∠OQF=90°,
∵OP=OQ≈6 400 km,FP≈330 km,
∴OF=OP+FP=6 730 km,
∴cos α=≈0.95.
(2)∵cos α≈0.95,cos 18°≈0.95,∴α≈18°,
∴≈2 010 km.
5.解析 设CH的高度为x m,
由题意得∠AHC=90°,∠CBH=45°,∠A=30°,
∴BH=CH=x m,AH=x m,
∵AH-BH=AB,∴x-x=20,解得x=10(+1)≈27.3.
答:“一心阁”CH的高度约为27.3 m.
6.解析 (1)∵斜坡CD的坡度为1∶2.4,
∴DE∶CE=1∶2.4=5∶12,
设DE=5x米,则CE=12x米,∴CD=13x米,
∵CD=13米,∴13x=13,∴x=1,∴DE=5米.
答:斜坡的高DE为5米.
(2)过点D作DF⊥PA 于点F,则AF=DE=5米,
∵∠PDF=45°,∴△DFP为等腰直角三角形,∴PF=DF.
设PF=DF=a米,
则AC=AE-CE=DF-CE=(a-12)米,AP=AF+PF=(5+a)米,
在Rt△APC 中,tan∠ACP=,
∴≈2,解得a≈29,
∴AP=PF+AF=29+5=34(米).
答:塔上观景点P距地面的高度约为34米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师大版数学九年级下学期
专项素养综合全练(十)
跨学科试题
类型一 跨物理学科试题
1.(2023河南永城一模)如图1,质量为m的小球从某高度处由静止开始下落到竖直放置的轻弹簧上并压缩弹簧(已知自然状态下,弹簧的初始长度为10 cm).从小球刚接触弹簧到将弹簧压缩至最短的过程中(不计空气阻力,弹簧在整个过程中始终发生弹性形变),得到小球的速度v(cm/s)和弹簧被压缩的长度Δl(cm)之间的关系图象如图2所示.根据图象,下列说法正确的是( )
图1 图2
A.小球从刚接触弹簧就开始减速
B.当小球下落至最低点时,弹簧的长度为4 cm
C.当弹簧被压缩至最短时,小球的速度最大
D.当小球的速度最大时,弹簧的长度为2 cm
2.如图,CD是平面镜,光线从A点出发经CD上点O反射后照射到B点,若入射角为α,反射角为β(反射角等于入射角),AC⊥CD于点C,BD⊥CD于点D,且AC=3,BD=6,CD=12,求tan α的值.
类型二 跨地理学科试题
3.(2023广东东莞光明中学一模)数学小组研究如下问题:东莞市地处北纬约23°的纬度上,求北纬23°纬线的长度,小组成员查阅相关资料,得到如下信息:
信息一:在地球仪上,与赤道平行的圆圈叫做纬线;
信息二:如图,赤道半径OA的长约为6 400千米,弦BC∥OA,以BC为直径的圆的周长就是北纬23°纬线的长度.
根据以上信息,北纬23°纬线的长度约是(参考数据:π≈3.14,sin 23°≈
0.39,cos 23°≈0.92,tan 23°≈0.42)( )
A.5 900千米 B.16 000千米 C.37 000千米 D.42 000千米
4.【国防科技】(2023湖北宜昌中考)2023年5月30日,“神舟十六号”航天飞船成功发射.飞船在离地球大约330 km的圆形轨道上,如图,当运行到地球表面P点的正上方F点时,从中直接看到地球表面一个最远的点是点Q.在Rt△OQF中,OP=OQ≈6 400 km.
(参考数据:cos 16°≈0.96,cos 18°≈0.95,cos 20°≈0.94,cos 22°≈0.93,π≈3.14)
(1)求cos α的值(精确到0.01);
(2)在☉O中,求的长(结果取整数).
类型三 跨语文学科试题
5.(2021湖南湘西州中考)有诗云:东山雨霁画屏开,风卷松声入耳来.一座楼阁镇四方,团结一心建家乡.1987年为庆祝湘西自治州成立三十周年,湘西州政府在花果山公园内修建了一座三层楼高的“一心阁”民族团结楼阁.如图,某学校数学实践活动小组为测量“一心阁”CH的高度,在楼前的平地上A处,观测到楼顶C处的仰角为30°,在平地上B处观测到楼顶C处的仰角为45°,并测得A、B两处相距20 m,求“一心阁”CH的高度.(结果保留小数点后一位,参考数据:≈1.41,≈1.73)
类型四 跨历史学科试题
6.(2023浙江宁波外国语学校三模)如图1,耸立在宁波海曙区的天封塔始建于唐武则天“天册万岁”至“万岁登封”(695—696)年间,因建塔年号始末“天”“封”而得名.如图2,在天封塔正前方有一斜坡CD,长为13米,坡度为1∶2.4,高为DE.某中学数学兴趣小组的同学利用测角仪在斜坡底的点C处测得塔上观景点P的仰角为64°,在斜坡顶的点D处测得塔上观景点P的仰角为45°(其中点A,C,E在同一直线上).
(1)求斜坡的高DE;
(2)求塔上观景点P距离地面的高度.(结果精确到1米,参考数据:
sin 64°≈0.9,tan 64°≈2)
图1 图2
答案全解全析
1.B 由图象可知,弹簧被压缩2 cm后小球开始减速,故选项A不合题意;由图象可知,当小球下落至最低点时,弹簧被压缩的长度为6 cm,此时弹簧的长度为10-6=4(cm),故选项B符合题意;由图象可知,当弹簧被压缩至最短时,小球的速度最小,为0 cm/s,故选项C不合题意;由图象可知,小球速度最大时,弹簧被压缩2 cm,此时弹簧的长度为10-2=
8 cm,故选项D不合题意.故选B.
2.解析 如图,由题意得OP⊥CD,∵AC⊥CD,∴AC∥OP,∴∠A=α,同理可得∠B=β,∵α=β,∴∠A=∠B,又∵∠ACO=∠BDO=90°,∴△AOC∽△BOD,∴
,解得OC=4,∴tan α=tan A=.
3.C 作OH⊥BC于H,∴BH=CH=BC,
∵OA∥BC,∴∠B=∠AOB=23°,∴cos B=cos 23°=,
∵OB=OA=6 400千米,∴BH≈6 400×0.92=5 888(千米),
∴BC=2BH=11 776(千米),
∴以BC为直径的圆的周长=π×11 776≈3.14×11 776=36 976.64≈
37 000(千米).
∴北纬23°纬线的长度约是37 000千米.故选C.
4.解析 (1)由题意知FQ是☉O的切线,
∴∠OQF=90°,
∵OP=OQ≈6 400 km,FP≈330 km,
∴OF=OP+FP=6 730 km,
∴cos α=≈0.95.
(2)∵cos α≈0.95,cos 18°≈0.95,∴α≈18°,
∴≈2 010 km.
5.解析 设CH的高度为x m,
由题意得∠AHC=90°,∠CBH=45°,∠A=30°,
∴BH=CH=x m,AH=x m,
∵AH-BH=AB,∴x-x=20,解得x=10(+1)≈27.3.
答:“一心阁”CH的高度约为27.3 m.
6.解析 (1)∵斜坡CD的坡度为1∶2.4,
∴DE∶CE=1∶2.4=5∶12,
设DE=5x米,则CE=12x米,∴CD=13x米,
∵CD=13米,∴13x=13,∴x=1,∴DE=5米.
答:斜坡的高DE为5米.
(2)过点D作DF⊥PA 于点F,则AF=DE=5米,
∵∠PDF=45°,∴△DFP为等腰直角三角形,∴PF=DF.
设PF=DF=a米,
则AC=AE-CE=DF-CE=(a-12)米,AP=AF+PF=(5+a)米,
在Rt△APC 中,tan∠ACP=,
∴≈2,解得a≈29,
∴AP=PF+AF=29+5=34(米).
答:塔上观景点P距地面的高度约为34米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
