2024北师大版数学九年级下学期课时练--第3课时 二次函数y=ax2+bx+c的图象与性质同步练习(含解析)
文档属性
| 名称 | 2024北师大版数学九年级下学期课时练--第3课时 二次函数y=ax2+bx+c的图象与性质同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 512.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 21:03:22 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024北师大版数学九年级下学期
第二章 二次函数
第3课时 二次函数y=ax2+bx+c的图象与性质
基础过关全练
知识点6 二次函数y=ax2+bx+c(a≠0)的图象与性质
27.(2023江西南昌外国语学校期末)把二次函数y=-x2-x+3用配方法化成y=a(x-h)2+k的形式时,应为( )
A.y=-(x-2)2+4
C.y=-+3
28.(2022四川成都模拟)关于二次函数y=-x2-2x+5,下列说法正确的是( )
A.y有最小值
B.图象的对称轴为直线x=1
C.当x<0时,y的值随x值的增大而增大
D.图象可由y=-x2的图象向左平移1个单位长度,再向上平移6个单位长度得到
29.【一题多解】在平面直角坐标系中,将抛物线y=x2-4x-4向左平移3个单位长度,再向上平移5个单位长度,得到抛物线的表达式为( )
A.y=(x+1)2-13 B.y=(x-5)2-13 C.y=(x-5)2-3 D.y=(x+1)2-3
30.(2023陕西宝鸡一模)已知二次函数y=x2-2x-3的自变量x1,x2,x3对应的函数值分别为y1,y2,y3.当-13时,y1,y2,y3三者之间的大小关系是( )
A.y131.已知二次函数y=-x2+2x+3.
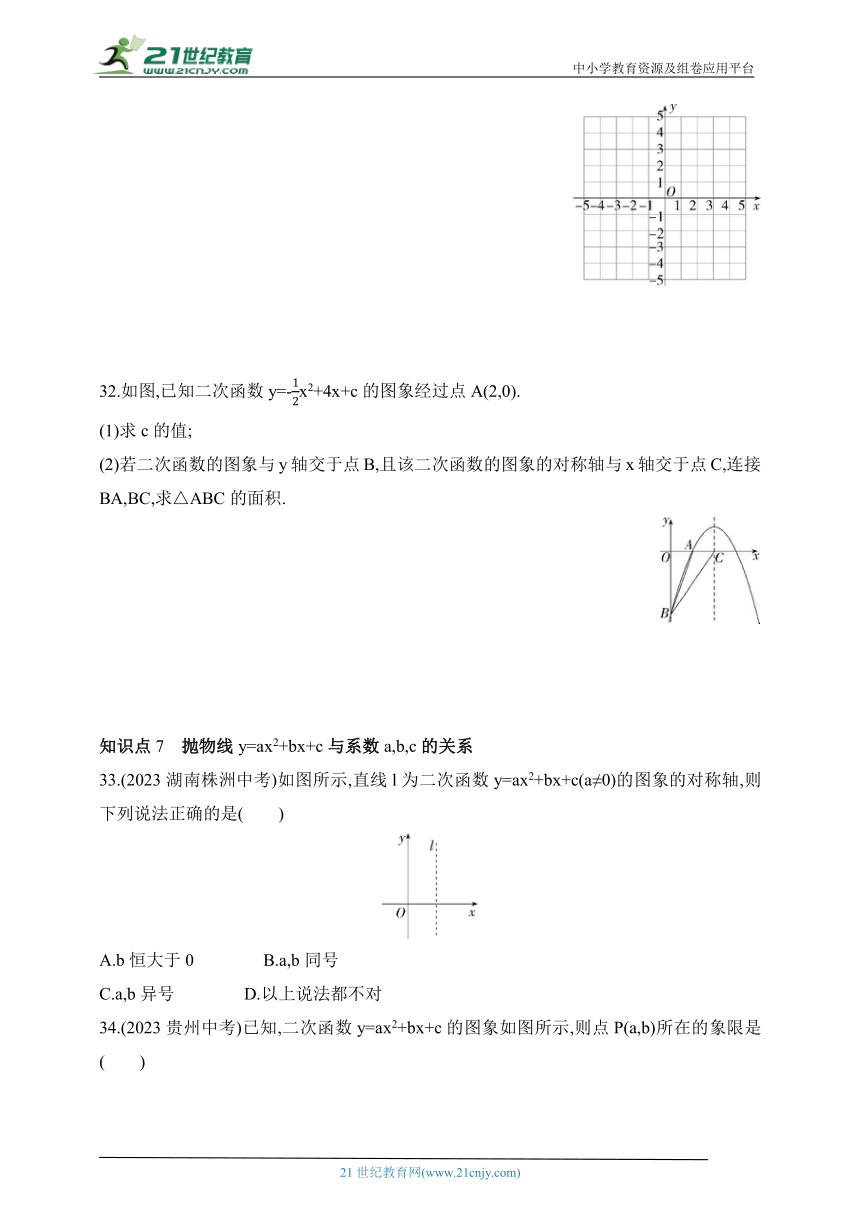
(1)求函数图象的顶点坐标,并在如图所示的平面直角坐标系中画出这个函数的图象;
(2)根据图象,直接写出:
①当函数值y为正数时,自变量x的取值范围;
②当-232.如图,已知二次函数y=-x2+4x+c的图象经过点A(2,0).
(1)求c的值;
(2)若二次函数的图象与y轴交于点B,且该二次函数的图象的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.
知识点7 抛物线y=ax2+bx+c与系数a,b,c的关系
33.(2023湖南株洲中考)如图所示,直线l为二次函数y=ax2+bx+c(a≠0)的图象的对称轴,则下列说法正确的是( )
A.b恒大于0 B.a,b同号
C.a,b异号 D.以上说法都不对
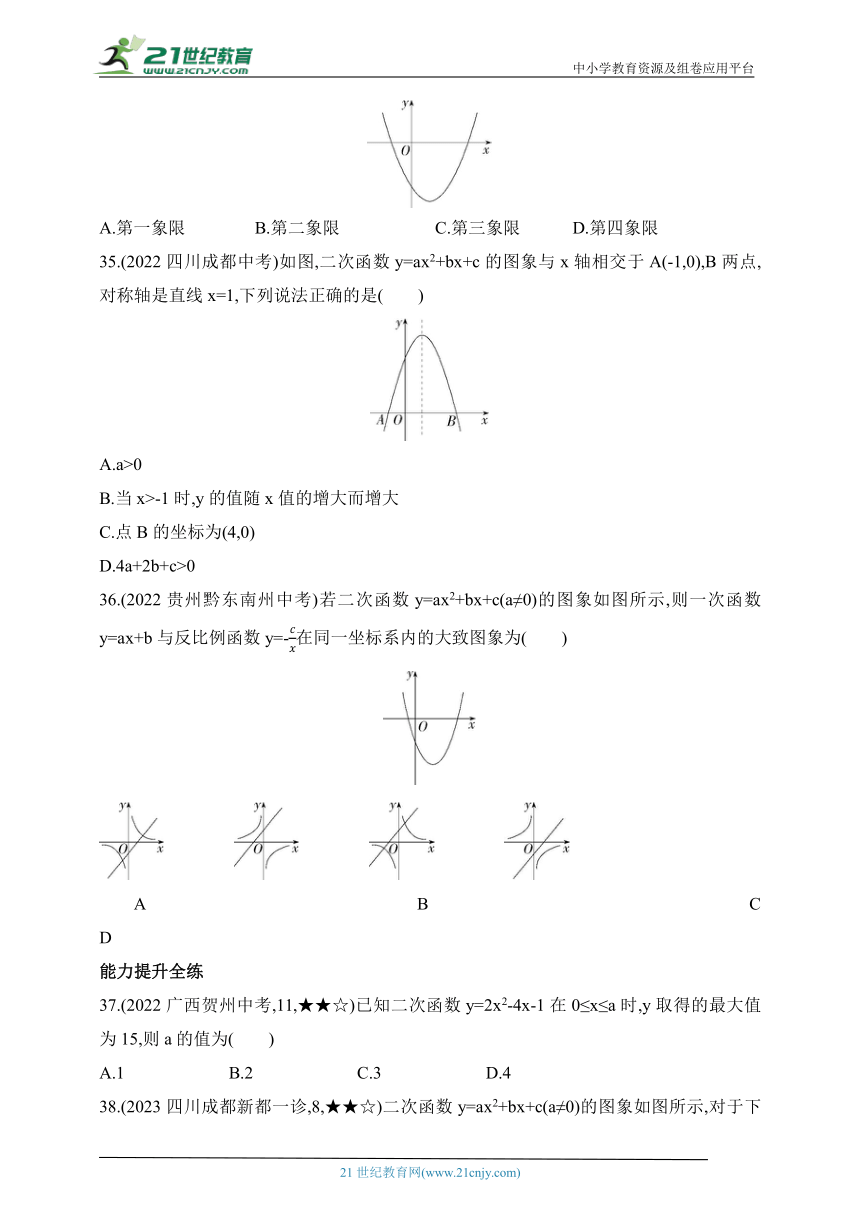
34.(2023贵州中考)已知,二次函数y=ax2+bx+c的图象如图所示,则点P(a,b)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
35.(2022四川成都中考)如图,二次函数y=ax2+bx+c的图象与x轴相交于A(-1,0),B两点,对称轴是直线x=1,下列说法正确的是( )
A.a>0
B.当x>-1时,y的值随x值的增大而增大
C.点B的坐标为(4,0)
D.4a+2b+c>0
36.(2022贵州黔东南州中考)若二次函数y=ax2+bx+c(a≠0)的图象如图所示,则一次函数y=ax+b与反比例函数y=-在同一坐标系内的大致图象为( )
A B C D
能力提升全练
37.(2022广西贺州中考,11,★★☆)已知二次函数y=2x2-4x-1在0≤x≤a时,y取得的最大值为15,则a的值为( )
A.1 B.2 C.3 D.4
38.(2023四川成都新都一诊,8,★★☆)二次函数y=ax2+bx+c(a≠0)的图象如图所示,对于下列结论:①abc>0;②2a+b=0;③9a+3b+c<0;④对于任意的实数m,总有a+b≥am2+bm.其中正确的个数是( )
A.1 B.2 C.3 D.4
39.(2023广东中考,10,★★☆)如图,抛物线y=ax2+c经过正方形OABC的三个顶点A,B,C,点B在y轴上,则ac的值为( )
A.-1 B.-2 C.-3 D.-4
40.(2023浙江杭州中考,8,★★☆)设二次函数y=a(x-m)(x-m-k)(a>0,m,k是实数),则( )
A.当k=2时,函数y的最小值为-a
B.当k=2时,函数y的最小值为-2a
C.当k=4时,函数y的最小值为-a
D.当k=4时,函数y的最小值为-2a
41.(2022陕西西安高新一中月考改编,9,★★☆)如图,正方形四个顶点的坐标依次为(1,1),(3,1),(3,3),(1,3).若抛物线y=ax2与正方形有公共点,则实数a的取值范围是 .
42.(2022贵州黔东南州中考,18,★★☆)在平面直角坐标系中,将抛物线y=x2+2x-1先绕原点旋转180°,再向下平移5个单位,所得到的抛物线的顶点坐标是 .
43.(2021浙江宁波中考,19,★★☆)如图,二次函数y=(x-1)(x-a)(a为常数)的图象的对称轴为直线x=2.
(1)求a的值;
(2)向下平移该二次函数的图象,使其经过原点,求平移后图象所对应的二次函数的表达式.
44.(2021浙江嘉兴中考,23,★★★)已知二次函数y=-x2+6x-5.
(1)求该二次函数图象的顶点坐标.
(2)当1≤x≤4时,函数的最大值和最小值分别为多少
(3)当t≤x≤t+3时,函数的最大值为m,最小值为n,若m-n=3,求t的值.
素养探究全练
45.【几何直观】(2022河北中考)如图,点P(a,3)在抛物线C:y=4-(6-x)2上,且在C的对称轴右侧.
(1)写出C的对称轴和y的最大值,并求a的值;
(2)坐标平面上放置一透明胶片,并在胶片上描画出点P及C的一段,分别记为P',C'.平移该胶片,使C'所在抛物线对应的函数解析式恰为y=-x2+6x-9.求点P'移动的最短路程.
答案全解全析
基础过关全练
27.C y=-(x+2)2+4.故选C.
28.D A.∵-1<0,∴函数图象开口向下,∴函数有最大值,因此该选项错误;
B.∵y=-x2-2x+5=-(x+1)2+6,∴二次函数y=-x2-2x+5的图象的对称轴为直线x=-1,因此该选项错误;
C.∵函数图象开口向下,对称轴为直线x=-1,∴当x<-1时,y的值随x值的增大而增大,因此该选项错误;
D.∵y=-x2的图象向左平移1个单位长度,再向上平移6个单位长度可得到y=-(x+1)2+6的图象,∴二次函数y=-x2-2x+5的图象可由y=-x2的图象向左平移1个单位长度,再向上平移6个单位长度得到,因此该选项正确.故选D.
29.D 解法一:∵y=x2-4x-4=(x-2)2-8,∴抛物线的顶点坐标为(2,-8),把点(2,-8)向左平移3个单位长度,再向上平移5个单位长度,得到的点的坐标为(-1,-3),∴平移后的抛物线的表达式为y=(x+1)2-3.
解法二:y=x2-4x-4=(x-2)2-8,根据抛物线的平移规律“左加右减、上加下减”,可得平移后的抛物线的表达式为y=(x-2+3)2-8+5=(x+1)2-3.
30.B ∵y=x2-2x-3=(x-1)2-4,∴抛物线开口向上,对称轴为直线x=1,顶点坐标为(1,-4),当y=0时,(x-1)2-4=0,解得x=-1或x=3,∴抛物线与x轴的两个交点坐标为(-1,0),(3,0),如图,∴当-13时,y231.解析 (1)∵y=-x2+2x+3=-(x-1)2+4,
∴函数图象的顶点坐标为(1,4).
函数的图象如图所示.
(2)根据图象可知:
①当函数值y为正数时,-1②当-2函数值y的取值范围是-532.解析 (1)把A(2,0)代入y=-x2+4x+c,得c=-6.
(2)由(1)可知该二次函数的表达式为y=-x2+4x-6.
由y=-x2+4x-6得点B的坐标为(0,-6),
∴OB=6.
∵抛物线的对称轴为直线x=-=4,
∴点C的坐标为(4,0),∴OC=4,
∴AC=OC-OA=4-2=2,
∴△ABC的面积为AC·OB=×2×6=6.
33.C ∵直线l为二次函数y=ax2+bx+c(a≠0)的图象的对称轴,∴对称轴在y轴右侧,
又∵对称轴为直线x=->0,当a<0时,b>0,当a>0时,b<0,∴a,b异号,故选C.
34.D ∵二次函数的图象的开口向上,对称轴在y轴的右侧,
∴a>0,->0,∴b<0,∴P(a,b)在第四象限.故选D.
35.D A.由题图可知抛物线开口向下,∴a<0,故选项A错误,不符合题意;
B.∵抛物线的对称轴是直线x=1,开口向下,
∴当x>1时,y随x的增大而减小,当x<1时,y随x的增大而增大,故选项B错误,不符合题意;
C.由A(-1,0),抛物线的对称轴是直线x=1可知,B点的坐标为(3,0),故选项C错误,不符合题意;
D.抛物线y=ax2+bx+c过点(2,4a+2b+c),由B(3,0)可知抛物线上横坐标为2的点在第一象限,
∴4a+2b+c>0,故选项D正确,符合题意.
故选D.
36.C ∵抛物线开口向上,∴a>0,∵抛物线的对称轴在y轴左侧,∴b>0,∵抛物线与y轴的交点在x轴下方,∴c<0,∴直线y=ax+b经过第一、二、三象限,反比例函数y=-的图象经过第一、三象限,故选C.
能力提升全练
37.D ∵y=2x2-4x-1=2(x-1)2-3,∴抛物线的对称轴为直线x=1,顶点坐标为(1,-3),当y=15时,2(x-1)2-3=15,解得x=4或x=-2,∵当0≤x≤a时,y的最大值为15,∴a=4,故选D.
38.C ∵抛物线开口向下,对称轴在y轴右侧,抛物线与y轴交于正半轴,∴a<0,b>0,c>0,∴abc<0,故①错误;∵对称轴为直线x=1,∴-=1,即2a+b=0,故②正确;∵对称轴为直线x=1,抛物线与x轴的一个交点在点(-1,0)右侧,∴抛物线与x轴的另一个交点在点(3,0)左侧,∴当x=3时,
y<0,∴9a+3b+c<0,故③正确;∵当x=m时,y=am2+bm+c,当x=1时,
y=a+b+c,当x=1时,函数值最大,∴am2+bm+c≤a+b+c,∴a+b≥am2+bm,故④正确.故选C.
39.B 如图,过A作AH⊥x轴于H,∵四边形ABCO是正方形,
∴∠AOB=45°,∴∠AOH=45°,∴AH=OH,设A(m,m)(m>0),则B(0,2m),∴,∴ac的值为-2,故选B.
40.A 令y=0,则a(x-m)(x-m-k)=0,∴x1=m,x2=m+k,∴二次函数y=a(x-m)(x-m-k)的图象与x轴的交点坐标是(m,0),(m+k,0),∴二次函数的图象的对称轴是直线x=,∵a>0,∴y有最小值,当x=时,y最小,此时y=aa,当k=2时,函数y的最小值为-a=-a;当k=4时,函数y的最小值为-a=-4a,故选A.
41.≤a≤3
解析 当抛物线经过(1,3)时,a=3,当抛物线经过(3,1)时,a=≤a≤3.
42.(1,-3)
解析 将抛物线y=x2+2x-1绕原点旋转180°后所得抛物线的解析式为-y=(-x)2+2(-x)-1,即y=-x2+2x+1,再将抛物线y=-x2+2x+1向下平移5个单位得抛物线y=-x2+2x+1-5=-x2+2x-4=-(x-1)2-3,∴所得到的抛物线的顶点坐标是(1,-3).
43.解析 (1)由二次函数y=(x-1)(x-a)(a为常数)知,该函数图象与x轴的交点坐标是(1,0)和(a,0).∵对称轴为直线x=2,∴=2,解得a=3.
(2)由(1)知a=3,
则该函数的表达式是y=(x-1)(x-3)=x2-4x+3.
∴该图象向下平移3个单位后经过原点,平移后图象所对应的二次函数的表达式是y=x2-4x.
44.解析 (1)∵y=-x2+6x-5=-(x-3)2+4,
∴图象的顶点坐标为(3,4).
(2)∵-1<0,∴函数图象开口向下,
∵顶点坐标为(3,4),∴当x=3时,y最大值=4,
∵当1≤x≤3时,y随着x的增大而增大,
∴当x=1时,y最小值=0,
∵当3∴当x=4时,y最小值=3.
∴当1≤x≤4时,函数的最大值为4,最小值为0.
(3)当t≤x≤t+3时,对t进行分类讨论,
①当t+3<3,即t<0时,y随着x的增大而增大,当x=t+3时,m=-(t+3)2+
6(t+3)-5=-t2+4,当x=t时,n=-t2+6t-5,∴m-n=-t2+4-(-t2+6t-5)=-6t+9,
∴-6t+9=3,解得t=1(不合题意,舍去).
②当0≤t<3时,顶点的横坐标在取值范围内,∴m=4,
当0≤t≤时,n=-t2+6t-5,∴m-n=4-(-t2+6t-5)=t2-6t+9,
∴t2-6t+9=3,解得t1=3-(不合题意,舍去);
当∴t2=3,解得t1=(不合题意,舍去).
③当t≥3时,y随着x的增大而减小,当x=t时,m=-t2+6t-5,
当x=t+3时,n=-(t+3)2+6(t+3)-5=-t2+4,∴m-n=-t2+6t-5-(-t2+4)=6t-9,∴6t-9=3,解得t=2(不合题意,舍去).
综上所述,t=3-.
素养探究全练
45.解析 (1)∵抛物线C:y=4-(6-x)2=-(x-6)2+4,
∴抛物线C的顶点坐标为(6,4),
∴抛物线C的对称轴为直线x=6,y的最大值为4,
当y=3时,3=-(x-6)2+4,∴x=5或x=7,
∵点P在对称轴的右侧,∴P(7,3),∴a=7.
(2)∵平移后的C'所在抛物线的解析式为y=-x2+6x-9=-(x-3)2,
∴平移后抛物线的顶点坐标为(3,0),
∵平移前抛物线的顶点坐标为(6,4),
∴点P'移动的最短路程==5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师大版数学九年级下学期
第二章 二次函数
第3课时 二次函数y=ax2+bx+c的图象与性质
基础过关全练
知识点6 二次函数y=ax2+bx+c(a≠0)的图象与性质
27.(2023江西南昌外国语学校期末)把二次函数y=-x2-x+3用配方法化成y=a(x-h)2+k的形式时,应为( )
A.y=-(x-2)2+4
C.y=-+3
28.(2022四川成都模拟)关于二次函数y=-x2-2x+5,下列说法正确的是( )
A.y有最小值
B.图象的对称轴为直线x=1
C.当x<0时,y的值随x值的增大而增大
D.图象可由y=-x2的图象向左平移1个单位长度,再向上平移6个单位长度得到
29.【一题多解】在平面直角坐标系中,将抛物线y=x2-4x-4向左平移3个单位长度,再向上平移5个单位长度,得到抛物线的表达式为( )
A.y=(x+1)2-13 B.y=(x-5)2-13 C.y=(x-5)2-3 D.y=(x+1)2-3
30.(2023陕西宝鸡一模)已知二次函数y=x2-2x-3的自变量x1,x2,x3对应的函数值分别为y1,y2,y3.当-1
A.y1
(1)求函数图象的顶点坐标,并在如图所示的平面直角坐标系中画出这个函数的图象;
(2)根据图象,直接写出:
①当函数值y为正数时,自变量x的取值范围;
②当-2
(1)求c的值;
(2)若二次函数的图象与y轴交于点B,且该二次函数的图象的对称轴与x轴交于点C,连接BA,BC,求△ABC的面积.
知识点7 抛物线y=ax2+bx+c与系数a,b,c的关系
33.(2023湖南株洲中考)如图所示,直线l为二次函数y=ax2+bx+c(a≠0)的图象的对称轴,则下列说法正确的是( )
A.b恒大于0 B.a,b同号
C.a,b异号 D.以上说法都不对
34.(2023贵州中考)已知,二次函数y=ax2+bx+c的图象如图所示,则点P(a,b)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
35.(2022四川成都中考)如图,二次函数y=ax2+bx+c的图象与x轴相交于A(-1,0),B两点,对称轴是直线x=1,下列说法正确的是( )
A.a>0
B.当x>-1时,y的值随x值的增大而增大
C.点B的坐标为(4,0)
D.4a+2b+c>0
36.(2022贵州黔东南州中考)若二次函数y=ax2+bx+c(a≠0)的图象如图所示,则一次函数y=ax+b与反比例函数y=-在同一坐标系内的大致图象为( )
A B C D
能力提升全练
37.(2022广西贺州中考,11,★★☆)已知二次函数y=2x2-4x-1在0≤x≤a时,y取得的最大值为15,则a的值为( )
A.1 B.2 C.3 D.4
38.(2023四川成都新都一诊,8,★★☆)二次函数y=ax2+bx+c(a≠0)的图象如图所示,对于下列结论:①abc>0;②2a+b=0;③9a+3b+c<0;④对于任意的实数m,总有a+b≥am2+bm.其中正确的个数是( )
A.1 B.2 C.3 D.4
39.(2023广东中考,10,★★☆)如图,抛物线y=ax2+c经过正方形OABC的三个顶点A,B,C,点B在y轴上,则ac的值为( )
A.-1 B.-2 C.-3 D.-4
40.(2023浙江杭州中考,8,★★☆)设二次函数y=a(x-m)(x-m-k)(a>0,m,k是实数),则( )
A.当k=2时,函数y的最小值为-a
B.当k=2时,函数y的最小值为-2a
C.当k=4时,函数y的最小值为-a
D.当k=4时,函数y的最小值为-2a
41.(2022陕西西安高新一中月考改编,9,★★☆)如图,正方形四个顶点的坐标依次为(1,1),(3,1),(3,3),(1,3).若抛物线y=ax2与正方形有公共点,则实数a的取值范围是 .
42.(2022贵州黔东南州中考,18,★★☆)在平面直角坐标系中,将抛物线y=x2+2x-1先绕原点旋转180°,再向下平移5个单位,所得到的抛物线的顶点坐标是 .
43.(2021浙江宁波中考,19,★★☆)如图,二次函数y=(x-1)(x-a)(a为常数)的图象的对称轴为直线x=2.
(1)求a的值;
(2)向下平移该二次函数的图象,使其经过原点,求平移后图象所对应的二次函数的表达式.
44.(2021浙江嘉兴中考,23,★★★)已知二次函数y=-x2+6x-5.
(1)求该二次函数图象的顶点坐标.
(2)当1≤x≤4时,函数的最大值和最小值分别为多少
(3)当t≤x≤t+3时,函数的最大值为m,最小值为n,若m-n=3,求t的值.
素养探究全练
45.【几何直观】(2022河北中考)如图,点P(a,3)在抛物线C:y=4-(6-x)2上,且在C的对称轴右侧.
(1)写出C的对称轴和y的最大值,并求a的值;
(2)坐标平面上放置一透明胶片,并在胶片上描画出点P及C的一段,分别记为P',C'.平移该胶片,使C'所在抛物线对应的函数解析式恰为y=-x2+6x-9.求点P'移动的最短路程.
答案全解全析
基础过关全练
27.C y=-(x+2)2+4.故选C.
28.D A.∵-1<0,∴函数图象开口向下,∴函数有最大值,因此该选项错误;
B.∵y=-x2-2x+5=-(x+1)2+6,∴二次函数y=-x2-2x+5的图象的对称轴为直线x=-1,因此该选项错误;
C.∵函数图象开口向下,对称轴为直线x=-1,∴当x<-1时,y的值随x值的增大而增大,因此该选项错误;
D.∵y=-x2的图象向左平移1个单位长度,再向上平移6个单位长度可得到y=-(x+1)2+6的图象,∴二次函数y=-x2-2x+5的图象可由y=-x2的图象向左平移1个单位长度,再向上平移6个单位长度得到,因此该选项正确.故选D.
29.D 解法一:∵y=x2-4x-4=(x-2)2-8,∴抛物线的顶点坐标为(2,-8),把点(2,-8)向左平移3个单位长度,再向上平移5个单位长度,得到的点的坐标为(-1,-3),∴平移后的抛物线的表达式为y=(x+1)2-3.
解法二:y=x2-4x-4=(x-2)2-8,根据抛物线的平移规律“左加右减、上加下减”,可得平移后的抛物线的表达式为y=(x-2+3)2-8+5=(x+1)2-3.
30.B ∵y=x2-2x-3=(x-1)2-4,∴抛物线开口向上,对称轴为直线x=1,顶点坐标为(1,-4),当y=0时,(x-1)2-4=0,解得x=-1或x=3,∴抛物线与x轴的两个交点坐标为(-1,0),(3,0),如图,∴当-1
∴函数图象的顶点坐标为(1,4).
函数的图象如图所示.
(2)根据图象可知:
①当函数值y为正数时,-1
(2)由(1)可知该二次函数的表达式为y=-x2+4x-6.
由y=-x2+4x-6得点B的坐标为(0,-6),
∴OB=6.
∵抛物线的对称轴为直线x=-=4,
∴点C的坐标为(4,0),∴OC=4,
∴AC=OC-OA=4-2=2,
∴△ABC的面积为AC·OB=×2×6=6.
33.C ∵直线l为二次函数y=ax2+bx+c(a≠0)的图象的对称轴,∴对称轴在y轴右侧,
又∵对称轴为直线x=->0,当a<0时,b>0,当a>0时,b<0,∴a,b异号,故选C.
34.D ∵二次函数的图象的开口向上,对称轴在y轴的右侧,
∴a>0,->0,∴b<0,∴P(a,b)在第四象限.故选D.
35.D A.由题图可知抛物线开口向下,∴a<0,故选项A错误,不符合题意;
B.∵抛物线的对称轴是直线x=1,开口向下,
∴当x>1时,y随x的增大而减小,当x<1时,y随x的增大而增大,故选项B错误,不符合题意;
C.由A(-1,0),抛物线的对称轴是直线x=1可知,B点的坐标为(3,0),故选项C错误,不符合题意;
D.抛物线y=ax2+bx+c过点(2,4a+2b+c),由B(3,0)可知抛物线上横坐标为2的点在第一象限,
∴4a+2b+c>0,故选项D正确,符合题意.
故选D.
36.C ∵抛物线开口向上,∴a>0,∵抛物线的对称轴在y轴左侧,∴b>0,∵抛物线与y轴的交点在x轴下方,∴c<0,∴直线y=ax+b经过第一、二、三象限,反比例函数y=-的图象经过第一、三象限,故选C.
能力提升全练
37.D ∵y=2x2-4x-1=2(x-1)2-3,∴抛物线的对称轴为直线x=1,顶点坐标为(1,-3),当y=15时,2(x-1)2-3=15,解得x=4或x=-2,∵当0≤x≤a时,y的最大值为15,∴a=4,故选D.
38.C ∵抛物线开口向下,对称轴在y轴右侧,抛物线与y轴交于正半轴,∴a<0,b>0,c>0,∴abc<0,故①错误;∵对称轴为直线x=1,∴-=1,即2a+b=0,故②正确;∵对称轴为直线x=1,抛物线与x轴的一个交点在点(-1,0)右侧,∴抛物线与x轴的另一个交点在点(3,0)左侧,∴当x=3时,
y<0,∴9a+3b+c<0,故③正确;∵当x=m时,y=am2+bm+c,当x=1时,
y=a+b+c,当x=1时,函数值最大,∴am2+bm+c≤a+b+c,∴a+b≥am2+bm,故④正确.故选C.
39.B 如图,过A作AH⊥x轴于H,∵四边形ABCO是正方形,
∴∠AOB=45°,∴∠AOH=45°,∴AH=OH,设A(m,m)(m>0),则B(0,2m),∴,∴ac的值为-2,故选B.
40.A 令y=0,则a(x-m)(x-m-k)=0,∴x1=m,x2=m+k,∴二次函数y=a(x-m)(x-m-k)的图象与x轴的交点坐标是(m,0),(m+k,0),∴二次函数的图象的对称轴是直线x=,∵a>0,∴y有最小值,当x=时,y最小,此时y=aa,当k=2时,函数y的最小值为-a=-a;当k=4时,函数y的最小值为-a=-4a,故选A.
41.≤a≤3
解析 当抛物线经过(1,3)时,a=3,当抛物线经过(3,1)时,a=≤a≤3.
42.(1,-3)
解析 将抛物线y=x2+2x-1绕原点旋转180°后所得抛物线的解析式为-y=(-x)2+2(-x)-1,即y=-x2+2x+1,再将抛物线y=-x2+2x+1向下平移5个单位得抛物线y=-x2+2x+1-5=-x2+2x-4=-(x-1)2-3,∴所得到的抛物线的顶点坐标是(1,-3).
43.解析 (1)由二次函数y=(x-1)(x-a)(a为常数)知,该函数图象与x轴的交点坐标是(1,0)和(a,0).∵对称轴为直线x=2,∴=2,解得a=3.
(2)由(1)知a=3,
则该函数的表达式是y=(x-1)(x-3)=x2-4x+3.
∴该图象向下平移3个单位后经过原点,平移后图象所对应的二次函数的表达式是y=x2-4x.
44.解析 (1)∵y=-x2+6x-5=-(x-3)2+4,
∴图象的顶点坐标为(3,4).
(2)∵-1<0,∴函数图象开口向下,
∵顶点坐标为(3,4),∴当x=3时,y最大值=4,
∵当1≤x≤3时,y随着x的增大而增大,
∴当x=1时,y最小值=0,
∵当3
∴当1≤x≤4时,函数的最大值为4,最小值为0.
(3)当t≤x≤t+3时,对t进行分类讨论,
①当t+3<3,即t<0时,y随着x的增大而增大,当x=t+3时,m=-(t+3)2+
6(t+3)-5=-t2+4,当x=t时,n=-t2+6t-5,∴m-n=-t2+4-(-t2+6t-5)=-6t+9,
∴-6t+9=3,解得t=1(不合题意,舍去).
②当0≤t<3时,顶点的横坐标在取值范围内,∴m=4,
当0≤t≤时,n=-t2+6t-5,∴m-n=4-(-t2+6t-5)=t2-6t+9,
∴t2-6t+9=3,解得t1=3-(不合题意,舍去);
当
③当t≥3时,y随着x的增大而减小,当x=t时,m=-t2+6t-5,
当x=t+3时,n=-(t+3)2+6(t+3)-5=-t2+4,∴m-n=-t2+6t-5-(-t2+4)=6t-9,∴6t-9=3,解得t=2(不合题意,舍去).
综上所述,t=3-.
素养探究全练
45.解析 (1)∵抛物线C:y=4-(6-x)2=-(x-6)2+4,
∴抛物线C的顶点坐标为(6,4),
∴抛物线C的对称轴为直线x=6,y的最大值为4,
当y=3时,3=-(x-6)2+4,∴x=5或x=7,
∵点P在对称轴的右侧,∴P(7,3),∴a=7.
(2)∵平移后的C'所在抛物线的解析式为y=-x2+6x-9=-(x-3)2,
∴平移后抛物线的顶点坐标为(3,0),
∵平移前抛物线的顶点坐标为(6,4),
∴点P'移动的最短路程==5.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
