2024北师大版数学九年级下学期课时练--第三章 圆素养综合检测题(含解析)
文档属性
| 名称 | 2024北师大版数学九年级下学期课时练--第三章 圆素养综合检测题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 685.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 21:05:38 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024北师大版数学九年级下学期
第三章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共30分)
1.下列说法正确的个数是( )
①半圆是弧;②长度相等的两条弧是等弧;③直径是圆中最长的弦;④三角形的外心是三角形三条内角平分线的交点.
A.1 B.2 C.3 D.4
2.(2023广东珠海斗门一模)已知☉O的半径为3 cm,点P到圆心O的距离OP=2 cm,则点P( )
A.在☉O外 B.在☉O上 C.在☉O内 D.无法确定
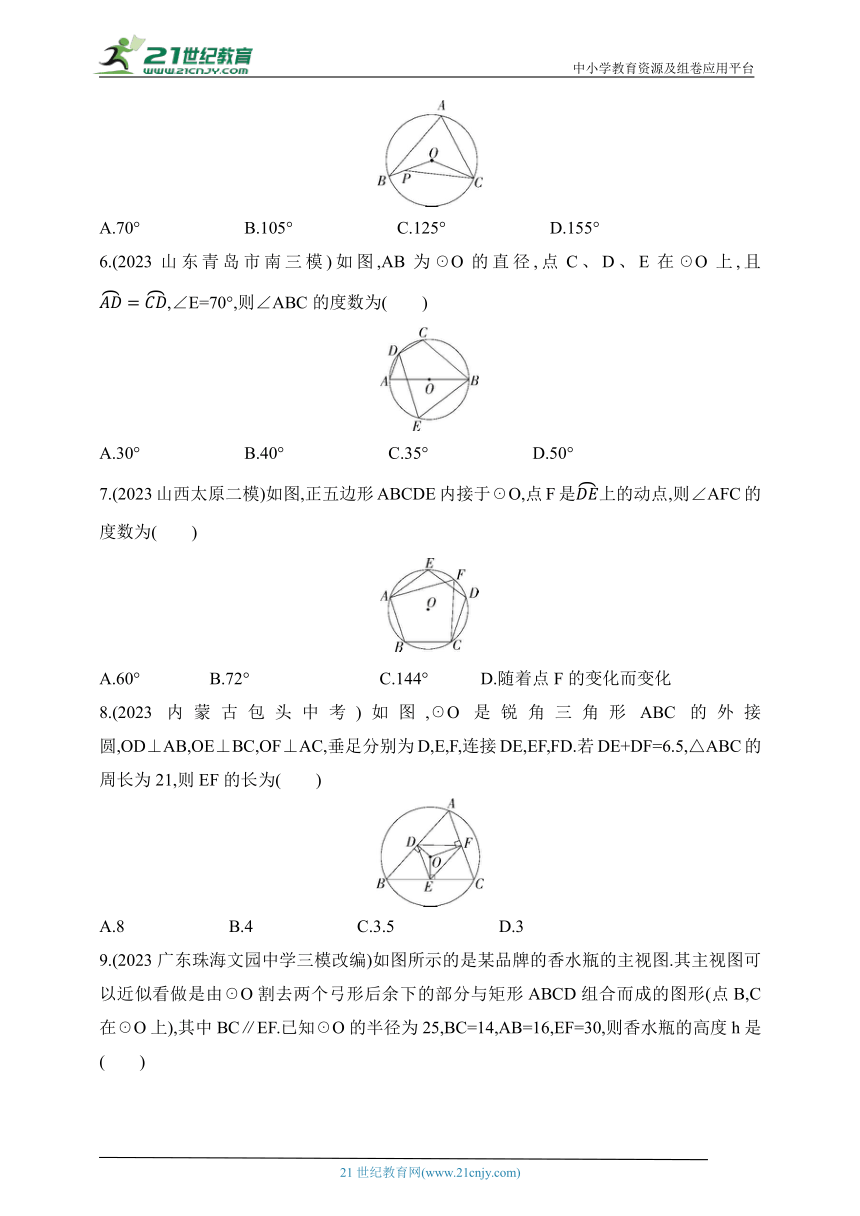
3.(2023河北师大实验中学期末)如图所示,在4×4的正方形网格中,A,B,C,D,O均在格点上,则点O是( )
A.△ACD的外心 B.△ACD的内心
C.△ABC的内心 D.△ABC的外心
4.(2021黑龙江哈尔滨中考)如图,AB是☉O的直径,BC是☉O的切线,点B为切点,若AB=8,tan∠BAC=,则BC的长为( )
A.8 B.7 C.10 D.6
5.(2023吉林中考)如图,AB,AC是☉O的弦,OB,OC是☉O的半径,点P为OB上任意一点(点P不与点B重合),连接CP.若∠BAC=70°,则
∠BPC的度数可能是( )
A.70° B.105° C.125° D.155°
6.(2023山东青岛市南三模)如图,AB为☉O的直径,点C、D、E在☉O上,且,∠E=70°,则∠ABC的度数为( )
A.30° B.40° C.35° D.50°
7.(2023山西太原二模)如图,正五边形ABCDE内接于☉O,点F是上的动点,则∠AFC的度数为( )
A.60° B.72° C.144° D.随着点F的变化而变化
8.(2023内蒙古包头中考)如图,☉O是锐角三角形ABC的外接圆,OD⊥AB,OE⊥BC,OF⊥AC,垂足分别为D,E,F,连接DE,EF,FD.若DE+DF=6.5,△ABC的周长为21,则EF的长为( )
A.8 B.4 C.3.5 D.3
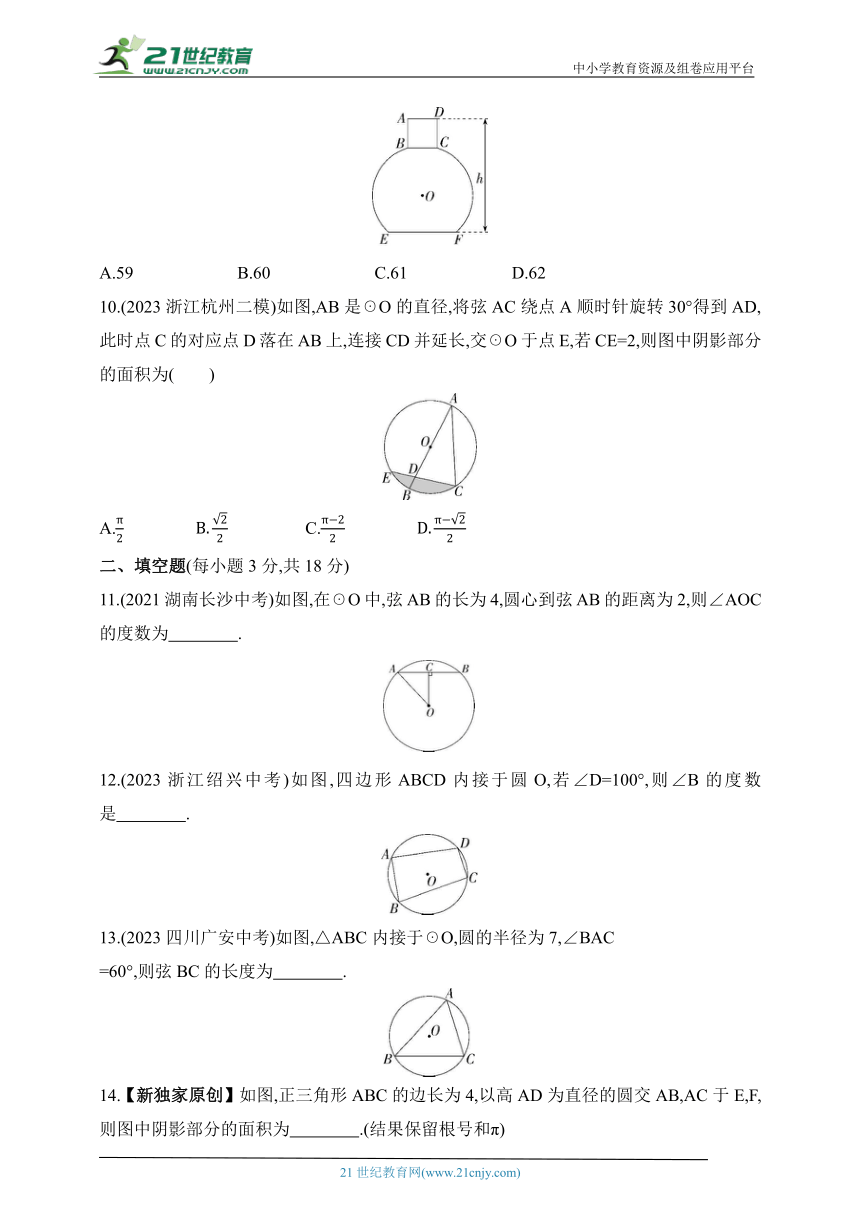
9.(2023广东珠海文园中学三模改编)如图所示的是某品牌的香水瓶的主视图.其主视图可以近似看做是由☉O割去两个弓形后余下的部分与矩形ABCD组合而成的图形(点B,C在☉O上),其中BC∥EF.已知☉O的半径为25,BC=14,AB=16,EF=30,则香水瓶的高度h是( )
A.59 B.60 C.61 D.62
10.(2023浙江杭州二模)如图,AB是☉O的直径,将弦AC绕点A顺时针旋转30°得到AD,此时点C的对应点D落在AB上,连接CD并延长,交☉O于点E,若CE=2,则图中阴影部分的面积为( )
A. C.
二、填空题(每小题3分,共18分)
11.(2021湖南长沙中考)如图,在☉O中,弦AB的长为4,圆心到弦AB的距离为2,则∠AOC的度数为 .
12.(2023浙江绍兴中考)如图,四边形ABCD内接于圆O,若∠D=100°,则∠B的度数是 .
13.(2023四川广安中考)如图,△ABC内接于☉O,圆的半径为7,∠BAC
=60°,则弦BC的长度为 .
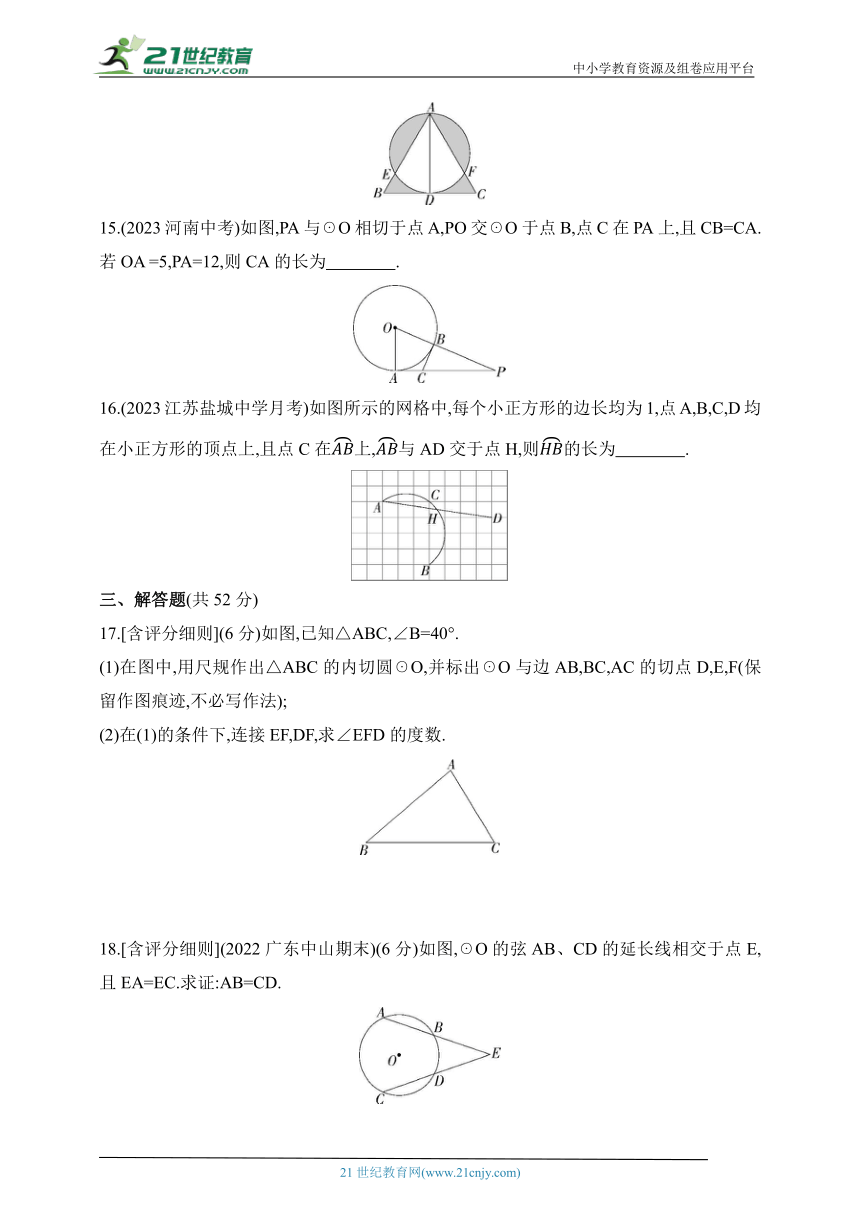
14.【新独家原创】如图,正三角形ABC的边长为4,以高AD为直径的圆交AB,AC于E,F,则图中阴影部分的面积为 .(结果保留根号和π)
15.(2023河南中考)如图,PA与☉O相切于点A,PO交☉O于点B,点C在PA上,且CB=CA.若OA =5,PA=12,则CA的长为 .
16.(2023江苏盐城中学月考)如图所示的网格中,每个小正方形的边长均为1,点A,B,C,D均在小正方形的顶点上,且点C在上,与AD交于点H,则的长为 .
三、解答题(共52分)
17.[含评分细则](6分)如图,已知△ABC,∠B=40°.
(1)在图中,用尺规作出△ABC的内切圆☉O,并标出☉O与边AB,BC,AC的切点D,E,F(保留作图痕迹,不必写作法);
(2)在(1)的条件下,连接EF,DF,求∠EFD的度数.
18.[含评分细则](2022广东中山期末)(6分)如图,☉O的弦AB、CD的延长线相交于点E,且EA=EC.求证:AB=CD.
19.[含评分细则](2023江西会昌模拟)(8分)证明:垂直于弦的直径平分弦以及弦所对的两条弧.
已知:如图,AB是☉O的直径,CD是☉O的弦, .
求证: .
证明:
20.[含评分细则](2023湖南郴州中考)(10分)如图,在☉O中,AB是直径,点C是圆上一点.在AB的延长线上取一点D,连接CD,使∠BCD=∠A.
(1)求证:直线CD是☉O的切线;
(2)若∠ACD=120°,CD=2,求图中阴影部分的面积(结果用含π的式子表示).
21.[含评分细则](2023河北中考)(10分)装有水的水槽放置在水平台面上,其横截面是以AB为直径的半圆O,AB=50 cm,如图1和图2所示,
MN为水面截线,GH为台面截线,MN∥GH.
计算 在图1中,已知MN=48 cm,作OC⊥MN于点C.
(1)求OC的长.
操作 将图1中的水槽沿GH向右做无滑动滚动,使水流出一部分,当∠ANM=30°时停止滚动,如图2.其中,半圆的中点为Q,GH与半圆的切点为E.连接OE交MN于点D.
探究 在图2中,
(2)操作后水面高度下降了多少
(3)连接OQ并延长交GH于点F,求线段EF与的长度,并比较大小.
图1 图2
22.[含评分细则](2022内蒙古包头中考)(12分)如图,AB为☉O的切线,C为切点,D是☉O上一点,过点D作DF⊥AB,垂足为F,DF交☉O于点E,连接EO并延长交☉O于点G,连接CG,OC,OD,已知∠DOE=
2∠CGE.
(1)若☉O的半径为5,求CG的长;
(2)试探究DE与EF之间的数量关系,写出并证明你的结论.(请用两种证法解答)
备用图
答案全解全析
1.B 圆的任意一条直径的端点把圆分成两条弧,每一条弧都叫做半圆,故①正确;长度相等的两条弧的度数不一定相等,故不一定是等弧,故②错误;直径是圆中最长的弦,故③正确;三角形的外心是三角形三边垂直平分线的交点,故④错误.故正确的为①③,共2个.故选B.
2.C ∵☉O的半径为3 cm,点P到圆心O的距离OP=2 cm,2<3,∴点P在☉O内,故选C.
3.A 设小正方形的边长为1,则由勾股定理可知OA=OD=OC=
,所以点O是△ACD的外心,故选A.
4.D ∵AB是☉O的直径,BC是☉O的切线,
∴AB⊥BC,∴∠ABC=90°,
∴tan∠BAC=,
∴BC=×8=6.故选D.
5.D 如图,连接BC,∵∠BAC=70°,∴∠BOC=2∠BAC=140°,
∵OB=OC,∴∠OBC=∠OCB==20°,
∵点P为OB上任意一点(点P不与点B重合),
∴0°≤∠OCP<20°,
∵∠BPC=∠BOC+∠OCP=140°+∠OCP,
∴140°≤∠BPC<160°,故选D.
6.B 如图,连接BD.
∵∠E=70°,∴∠A=∠E=70°,
∵AB为☉O的直径,∴∠ADB=90°,∴∠ABD=20°,
∵,∴∠ABD=∠CBD,
∴∠ABC=2∠ABD=40°,故选B.
7.B 如图,连接OA、OB、OC,
∵五边形ABCDE是☉O的内接正五边形,
∴∠AOB=∠BOC==72°,∴∠AOC=144°,∴∠AFC=∠AOC=72°,故选B.
8.B ∵OD⊥AB,OE⊥BC,OF⊥AC,∴AD=BD,AF=CF,BE=CE,
∴DE,DF,EF是△ABC的中位线,∴DE=
×21=10.5,
∵DE+DF=6.5,∴EF=10.5-6.5=4,故选B.
9.B 如图,作OG⊥BC交BC于点G,延长GO交EF于点H,连接BO、EO,
∵OG⊥BC,BC=14,∴BG=BC=7,
∵BO=EO=25,∴在Rt△BGO中,GO==24,
∵BC∥EF,OG⊥BC,∴OH⊥EF,∴EH=EF=15,
在Rt△EHO中,HO==20,
∴h=HO+GO+AB=20+24+16=60,故选B.
10.C 连接OE,OC,BC,
由旋转知AC=AD,∠CAD=30°,
∴∠BOC=60°,∠ACE=(180°-30°)÷2=75°,
∵AB是直径,∴∠ACB=90°,∴∠BCE=90°-∠ACE=15°,
∴∠BOE=2∠BCE=30°,∴∠EOC=90°,即△EOC为等腰直角三角形,∵CE=2,∴OE=OC=,
∴S阴影=S扇形OEC-S△OEC=,故选C.
11.45°
解析 ∵OC⊥AB,∴AC=BC=×4=2,∴OC=AC=2,∴△AOC为等腰直角三角形,∴∠AOC=45°.
12.80°
解析 ∵四边形ABCD内接于圆O,∴∠B+∠D=180°,
∵∠D=100°,∴∠B=80°.
13.7
解析 作OD⊥BC于点D,连接OB,OC,如图所示,
∵∠BAC=60°,∴∠BOC=2∠BAC=120°,
∵OD⊥BC,OB=OC,∴∠BOD=∠BOC=60°,BD=CD,
∴BD=BO·sin∠BOD=7×sin 60°=7×,
故答案为7.
14.π+
解析 如图,设圆心为O,连接EO,过O作OG⊥AE于G.
∵△ABC为正三角形,且其边长为4,AD为高,
∴AB=4,BD=×4=2,∠B=60°,∠BAD=∠BAC=30°.
∴∠DOE=60°,AD=ABsin B=4×sin 60°=4×
.
∴AG=AOcos∠GAO=×cos 30°=.
∴S△AOE=2S△AOG=2×AG·OG=.
∵S扇形OED=,∴S空白=2(S△AOE+S扇形OED)=+π.
∴S阴影=S☉O+S△ABC-2S空白=π·OD2+BC·AD-2×.
15.
解析 连接OC,
∵PA与☉O相切于点A,∴∠OAP=90°,
∵OA=OB,OC=OC,CA=CB,∴△OAC≌△OBC(SSS),
∴∠OAP=∠OBC=90°,
在Rt△OAP中,OA=5,PA=12,∴OP==13,
∵△OAC的面积+△OCP的面积=△OAP的面积,
∴OA·AC+OP·BC=OA·AP,∴OA·AC+OP·BC=OA·AP,
∴5AC+13BC=5×12,∴AC=BC=,故答案为.
16.
解析 如图,连接AB,BD,设AB的中点为O,连接OH.
∵∠ACB=90°,∴AB为直径,AB的中点O为圆心,
根据勾股定理得AB=BD=5,AD=5,
∵AB2+BD2=AD2,∴∠ABD=90°,∴∠BAD=∠BDA=45°,
∵OA=OH,∴∠AHO=∠OAH=45°,∴∠BOH=90°,
∴弧HB的长为.
17.解析 (1)如图.3分
(2)如图,连接OD,易知∠ODB=∠OEB=90°.4分
又∵∠ABC=40°,
∴∠DOE=140°,5分
∴∠EFD=∠DOE=70°.6分
18.证明 如图,连接AC,
∵EA=EC,
∴∠EAC=∠ECA,
∴,3分
∴,即,5分
∴AB=CD.6分
19.解析 已知:如图,AB是☉O的直径,CD是☉O的弦,AB⊥CD,垂足为E.2分
求证:CE=DE,.4分
证明:连接OC、OD,
在△OCD中,∵AB⊥CD,OC=OD,
∴CE=DE,∠COB=∠DOB,6分
∴,∠AOC=∠AOD,7分
∴.8分
20.解析 (1)证明:连接OC,1分
∵AB是直径,∴∠ACB=∠OCA+∠OCB=90°,2分
∵OA=OC,∠BCD=∠A,∴∠OCA=∠A=∠BCD,3分
∴∠BCD+∠OCB=∠OCD=90°,∴OC⊥CD,4分
∵OC是☉O的半径,∴直线CD是☉O的切线.5分
(2)∵∠ACD=120°,∠ACB=90°,
∴∠A=∠BCD=120°-90°=30°,6分
∴∠DOC=2∠A=60°,7分
在Rt△OCD中,tan∠DOC==tan 60°,CD=2
,解得OC=2,8分
∴阴影部分的面积=S△OCD-S扇形BOC
=.10分
21.解析 (1)连接OM,
∵O为圆心,OC⊥MN于点C,MN=48 cm,
∴MC=MN=24 cm,1分
∵AB=50 cm,∴OM=AB=25 cm,2分
在Rt△OMC 中,OC==7(cm).3分
(2)∵GH与半圆的切点为E,∴OE⊥GH,4分
∵MN∥GH,∴OE⊥MN于点D,
∵∠ANM=30°,ON=25 cm,
∴OD= cm,5分
∴操作后水面高度下降了 cm.6分
(3)∵OE⊥MN于点D,∠ANM=30°,∴∠DOB=60°,
∵半圆的中点为Q,∴,∴∠QOB=90°,7分
∴∠QOE=30°,
∴EF=tan∠QOE·OE=(cm),8分
(cm),9分
∵>0,
∴EF的长度>的长度.10分
22.解析 (1)如图,连接CE,
∵,∴∠COE=2∠CGE.
∵∠DOE=2∠CGE,∴∠COE=∠DOE,
∵AB为☉O的切线,C为切点,∴OC⊥AB,
∴∠OCB=90°,∵DF⊥AB,∴∠DFB=90°,
∴∠OCB=∠DFB=90°,∴OC∥DF,
∴∠COE=∠OED,∴∠DOE=∠OED,∴OD=DE,
∵OD=OE,∴OD=OE=DE,
∴△ODE是等边三角形,
∴∠DOE=60°,∴∠CGE=30°.
∵☉O的半径为5,∴GE=10,
∵GE是☉O的直径,∴∠GCE=90°,
在Rt△GCE中,CG=GE·cos∠CGE=10×cos 30°=10×.5分
(2)DE=2EF.6分
证法一:∵∠COE=∠DOE=60°,∴CE=DE,
∵OC=OE,∴△OCE为等边三角形,∴∠OCE=60°,
∵∠OCB=90°,∴∠ECF=30°,
∴EF=DE,即DE=2EF.9分
证法二:如图,过点O作OH⊥DF于H,
∴∠OHF=90°,又∵∠OCB=∠DFC=90°,
∴四边形OCFH是矩形,∴CF=OH,
∵△ODE是等边三角形,OH⊥DF,∴DH=EH,
∵∠COE=60°,OC=OE,∴△OCE为等边三角形,∴CE=OE,
又∵CF=OH,∠CFE=∠OHE=90°,
∴Rt△CFE≌Rt△OHE(HL),∴EF=EH,
∴DH=EH=EF,∴DE=2EF.12分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师大版数学九年级下学期
第三章 素养综合检测
(满分100分,限时60分钟)
一、选择题(每小题3分,共30分)
1.下列说法正确的个数是( )
①半圆是弧;②长度相等的两条弧是等弧;③直径是圆中最长的弦;④三角形的外心是三角形三条内角平分线的交点.
A.1 B.2 C.3 D.4
2.(2023广东珠海斗门一模)已知☉O的半径为3 cm,点P到圆心O的距离OP=2 cm,则点P( )
A.在☉O外 B.在☉O上 C.在☉O内 D.无法确定
3.(2023河北师大实验中学期末)如图所示,在4×4的正方形网格中,A,B,C,D,O均在格点上,则点O是( )
A.△ACD的外心 B.△ACD的内心
C.△ABC的内心 D.△ABC的外心
4.(2021黑龙江哈尔滨中考)如图,AB是☉O的直径,BC是☉O的切线,点B为切点,若AB=8,tan∠BAC=,则BC的长为( )
A.8 B.7 C.10 D.6
5.(2023吉林中考)如图,AB,AC是☉O的弦,OB,OC是☉O的半径,点P为OB上任意一点(点P不与点B重合),连接CP.若∠BAC=70°,则
∠BPC的度数可能是( )
A.70° B.105° C.125° D.155°
6.(2023山东青岛市南三模)如图,AB为☉O的直径,点C、D、E在☉O上,且,∠E=70°,则∠ABC的度数为( )
A.30° B.40° C.35° D.50°
7.(2023山西太原二模)如图,正五边形ABCDE内接于☉O,点F是上的动点,则∠AFC的度数为( )
A.60° B.72° C.144° D.随着点F的变化而变化
8.(2023内蒙古包头中考)如图,☉O是锐角三角形ABC的外接圆,OD⊥AB,OE⊥BC,OF⊥AC,垂足分别为D,E,F,连接DE,EF,FD.若DE+DF=6.5,△ABC的周长为21,则EF的长为( )
A.8 B.4 C.3.5 D.3
9.(2023广东珠海文园中学三模改编)如图所示的是某品牌的香水瓶的主视图.其主视图可以近似看做是由☉O割去两个弓形后余下的部分与矩形ABCD组合而成的图形(点B,C在☉O上),其中BC∥EF.已知☉O的半径为25,BC=14,AB=16,EF=30,则香水瓶的高度h是( )
A.59 B.60 C.61 D.62
10.(2023浙江杭州二模)如图,AB是☉O的直径,将弦AC绕点A顺时针旋转30°得到AD,此时点C的对应点D落在AB上,连接CD并延长,交☉O于点E,若CE=2,则图中阴影部分的面积为( )
A. C.
二、填空题(每小题3分,共18分)
11.(2021湖南长沙中考)如图,在☉O中,弦AB的长为4,圆心到弦AB的距离为2,则∠AOC的度数为 .
12.(2023浙江绍兴中考)如图,四边形ABCD内接于圆O,若∠D=100°,则∠B的度数是 .
13.(2023四川广安中考)如图,△ABC内接于☉O,圆的半径为7,∠BAC
=60°,则弦BC的长度为 .
14.【新独家原创】如图,正三角形ABC的边长为4,以高AD为直径的圆交AB,AC于E,F,则图中阴影部分的面积为 .(结果保留根号和π)
15.(2023河南中考)如图,PA与☉O相切于点A,PO交☉O于点B,点C在PA上,且CB=CA.若OA =5,PA=12,则CA的长为 .
16.(2023江苏盐城中学月考)如图所示的网格中,每个小正方形的边长均为1,点A,B,C,D均在小正方形的顶点上,且点C在上,与AD交于点H,则的长为 .
三、解答题(共52分)
17.[含评分细则](6分)如图,已知△ABC,∠B=40°.
(1)在图中,用尺规作出△ABC的内切圆☉O,并标出☉O与边AB,BC,AC的切点D,E,F(保留作图痕迹,不必写作法);
(2)在(1)的条件下,连接EF,DF,求∠EFD的度数.
18.[含评分细则](2022广东中山期末)(6分)如图,☉O的弦AB、CD的延长线相交于点E,且EA=EC.求证:AB=CD.
19.[含评分细则](2023江西会昌模拟)(8分)证明:垂直于弦的直径平分弦以及弦所对的两条弧.
已知:如图,AB是☉O的直径,CD是☉O的弦, .
求证: .
证明:
20.[含评分细则](2023湖南郴州中考)(10分)如图,在☉O中,AB是直径,点C是圆上一点.在AB的延长线上取一点D,连接CD,使∠BCD=∠A.
(1)求证:直线CD是☉O的切线;
(2)若∠ACD=120°,CD=2,求图中阴影部分的面积(结果用含π的式子表示).
21.[含评分细则](2023河北中考)(10分)装有水的水槽放置在水平台面上,其横截面是以AB为直径的半圆O,AB=50 cm,如图1和图2所示,
MN为水面截线,GH为台面截线,MN∥GH.
计算 在图1中,已知MN=48 cm,作OC⊥MN于点C.
(1)求OC的长.
操作 将图1中的水槽沿GH向右做无滑动滚动,使水流出一部分,当∠ANM=30°时停止滚动,如图2.其中,半圆的中点为Q,GH与半圆的切点为E.连接OE交MN于点D.
探究 在图2中,
(2)操作后水面高度下降了多少
(3)连接OQ并延长交GH于点F,求线段EF与的长度,并比较大小.
图1 图2
22.[含评分细则](2022内蒙古包头中考)(12分)如图,AB为☉O的切线,C为切点,D是☉O上一点,过点D作DF⊥AB,垂足为F,DF交☉O于点E,连接EO并延长交☉O于点G,连接CG,OC,OD,已知∠DOE=
2∠CGE.
(1)若☉O的半径为5,求CG的长;
(2)试探究DE与EF之间的数量关系,写出并证明你的结论.(请用两种证法解答)
备用图
答案全解全析
1.B 圆的任意一条直径的端点把圆分成两条弧,每一条弧都叫做半圆,故①正确;长度相等的两条弧的度数不一定相等,故不一定是等弧,故②错误;直径是圆中最长的弦,故③正确;三角形的外心是三角形三边垂直平分线的交点,故④错误.故正确的为①③,共2个.故选B.
2.C ∵☉O的半径为3 cm,点P到圆心O的距离OP=2 cm,2<3,∴点P在☉O内,故选C.
3.A 设小正方形的边长为1,则由勾股定理可知OA=OD=OC=
,所以点O是△ACD的外心,故选A.
4.D ∵AB是☉O的直径,BC是☉O的切线,
∴AB⊥BC,∴∠ABC=90°,
∴tan∠BAC=,
∴BC=×8=6.故选D.
5.D 如图,连接BC,∵∠BAC=70°,∴∠BOC=2∠BAC=140°,
∵OB=OC,∴∠OBC=∠OCB==20°,
∵点P为OB上任意一点(点P不与点B重合),
∴0°≤∠OCP<20°,
∵∠BPC=∠BOC+∠OCP=140°+∠OCP,
∴140°≤∠BPC<160°,故选D.
6.B 如图,连接BD.
∵∠E=70°,∴∠A=∠E=70°,
∵AB为☉O的直径,∴∠ADB=90°,∴∠ABD=20°,
∵,∴∠ABD=∠CBD,
∴∠ABC=2∠ABD=40°,故选B.
7.B 如图,连接OA、OB、OC,
∵五边形ABCDE是☉O的内接正五边形,
∴∠AOB=∠BOC==72°,∴∠AOC=144°,∴∠AFC=∠AOC=72°,故选B.
8.B ∵OD⊥AB,OE⊥BC,OF⊥AC,∴AD=BD,AF=CF,BE=CE,
∴DE,DF,EF是△ABC的中位线,∴DE=
×21=10.5,
∵DE+DF=6.5,∴EF=10.5-6.5=4,故选B.
9.B 如图,作OG⊥BC交BC于点G,延长GO交EF于点H,连接BO、EO,
∵OG⊥BC,BC=14,∴BG=BC=7,
∵BO=EO=25,∴在Rt△BGO中,GO==24,
∵BC∥EF,OG⊥BC,∴OH⊥EF,∴EH=EF=15,
在Rt△EHO中,HO==20,
∴h=HO+GO+AB=20+24+16=60,故选B.
10.C 连接OE,OC,BC,
由旋转知AC=AD,∠CAD=30°,
∴∠BOC=60°,∠ACE=(180°-30°)÷2=75°,
∵AB是直径,∴∠ACB=90°,∴∠BCE=90°-∠ACE=15°,
∴∠BOE=2∠BCE=30°,∴∠EOC=90°,即△EOC为等腰直角三角形,∵CE=2,∴OE=OC=,
∴S阴影=S扇形OEC-S△OEC=,故选C.
11.45°
解析 ∵OC⊥AB,∴AC=BC=×4=2,∴OC=AC=2,∴△AOC为等腰直角三角形,∴∠AOC=45°.
12.80°
解析 ∵四边形ABCD内接于圆O,∴∠B+∠D=180°,
∵∠D=100°,∴∠B=80°.
13.7
解析 作OD⊥BC于点D,连接OB,OC,如图所示,
∵∠BAC=60°,∴∠BOC=2∠BAC=120°,
∵OD⊥BC,OB=OC,∴∠BOD=∠BOC=60°,BD=CD,
∴BD=BO·sin∠BOD=7×sin 60°=7×,
故答案为7.
14.π+
解析 如图,设圆心为O,连接EO,过O作OG⊥AE于G.
∵△ABC为正三角形,且其边长为4,AD为高,
∴AB=4,BD=×4=2,∠B=60°,∠BAD=∠BAC=30°.
∴∠DOE=60°,AD=ABsin B=4×sin 60°=4×
.
∴AG=AOcos∠GAO=×cos 30°=.
∴S△AOE=2S△AOG=2×AG·OG=.
∵S扇形OED=,∴S空白=2(S△AOE+S扇形OED)=+π.
∴S阴影=S☉O+S△ABC-2S空白=π·OD2+BC·AD-2×.
15.
解析 连接OC,
∵PA与☉O相切于点A,∴∠OAP=90°,
∵OA=OB,OC=OC,CA=CB,∴△OAC≌△OBC(SSS),
∴∠OAP=∠OBC=90°,
在Rt△OAP中,OA=5,PA=12,∴OP==13,
∵△OAC的面积+△OCP的面积=△OAP的面积,
∴OA·AC+OP·BC=OA·AP,∴OA·AC+OP·BC=OA·AP,
∴5AC+13BC=5×12,∴AC=BC=,故答案为.
16.
解析 如图,连接AB,BD,设AB的中点为O,连接OH.
∵∠ACB=90°,∴AB为直径,AB的中点O为圆心,
根据勾股定理得AB=BD=5,AD=5,
∵AB2+BD2=AD2,∴∠ABD=90°,∴∠BAD=∠BDA=45°,
∵OA=OH,∴∠AHO=∠OAH=45°,∴∠BOH=90°,
∴弧HB的长为.
17.解析 (1)如图.3分
(2)如图,连接OD,易知∠ODB=∠OEB=90°.4分
又∵∠ABC=40°,
∴∠DOE=140°,5分
∴∠EFD=∠DOE=70°.6分
18.证明 如图,连接AC,
∵EA=EC,
∴∠EAC=∠ECA,
∴,3分
∴,即,5分
∴AB=CD.6分
19.解析 已知:如图,AB是☉O的直径,CD是☉O的弦,AB⊥CD,垂足为E.2分
求证:CE=DE,.4分
证明:连接OC、OD,
在△OCD中,∵AB⊥CD,OC=OD,
∴CE=DE,∠COB=∠DOB,6分
∴,∠AOC=∠AOD,7分
∴.8分
20.解析 (1)证明:连接OC,1分
∵AB是直径,∴∠ACB=∠OCA+∠OCB=90°,2分
∵OA=OC,∠BCD=∠A,∴∠OCA=∠A=∠BCD,3分
∴∠BCD+∠OCB=∠OCD=90°,∴OC⊥CD,4分
∵OC是☉O的半径,∴直线CD是☉O的切线.5分
(2)∵∠ACD=120°,∠ACB=90°,
∴∠A=∠BCD=120°-90°=30°,6分
∴∠DOC=2∠A=60°,7分
在Rt△OCD中,tan∠DOC==tan 60°,CD=2
,解得OC=2,8分
∴阴影部分的面积=S△OCD-S扇形BOC
=.10分
21.解析 (1)连接OM,
∵O为圆心,OC⊥MN于点C,MN=48 cm,
∴MC=MN=24 cm,1分
∵AB=50 cm,∴OM=AB=25 cm,2分
在Rt△OMC 中,OC==7(cm).3分
(2)∵GH与半圆的切点为E,∴OE⊥GH,4分
∵MN∥GH,∴OE⊥MN于点D,
∵∠ANM=30°,ON=25 cm,
∴OD= cm,5分
∴操作后水面高度下降了 cm.6分
(3)∵OE⊥MN于点D,∠ANM=30°,∴∠DOB=60°,
∵半圆的中点为Q,∴,∴∠QOB=90°,7分
∴∠QOE=30°,
∴EF=tan∠QOE·OE=(cm),8分
(cm),9分
∵>0,
∴EF的长度>的长度.10分
22.解析 (1)如图,连接CE,
∵,∴∠COE=2∠CGE.
∵∠DOE=2∠CGE,∴∠COE=∠DOE,
∵AB为☉O的切线,C为切点,∴OC⊥AB,
∴∠OCB=90°,∵DF⊥AB,∴∠DFB=90°,
∴∠OCB=∠DFB=90°,∴OC∥DF,
∴∠COE=∠OED,∴∠DOE=∠OED,∴OD=DE,
∵OD=OE,∴OD=OE=DE,
∴△ODE是等边三角形,
∴∠DOE=60°,∴∠CGE=30°.
∵☉O的半径为5,∴GE=10,
∵GE是☉O的直径,∴∠GCE=90°,
在Rt△GCE中,CG=GE·cos∠CGE=10×cos 30°=10×.5分
(2)DE=2EF.6分
证法一:∵∠COE=∠DOE=60°,∴CE=DE,
∵OC=OE,∴△OCE为等边三角形,∴∠OCE=60°,
∵∠OCB=90°,∴∠ECF=30°,
∴EF=DE,即DE=2EF.9分
证法二:如图,过点O作OH⊥DF于H,
∴∠OHF=90°,又∵∠OCB=∠DFC=90°,
∴四边形OCFH是矩形,∴CF=OH,
∵△ODE是等边三角形,OH⊥DF,∴DH=EH,
∵∠COE=60°,OC=OE,∴△OCE为等边三角形,∴CE=OE,
又∵CF=OH,∠CFE=∠OHE=90°,
∴Rt△CFE≌Rt△OHE(HL),∴EF=EH,
∴DH=EH=EF,∴DE=2EF.12分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
