2024北师大版九年级下学期期中素养综合测试数学试题(含解析)
文档属性
| 名称 | 2024北师大版九年级下学期期中素养综合测试数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 596.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 21:07:28 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2024北师大版数学九年级下学期
期中素养综合测试
(满分120分,限时100分钟)
一、选择题(每小题3分,共30分)
1.(2023辽宁鞍山立山一模)下列函数是二次函数的是( )
A.y=x+ B.y=3(x-1)2
C.y=ax2+bx+c D.y=+3x
2.(2023黑龙江哈尔滨平房二模)如图,在Rt△ABC中,∠C=90°,AC=6,BC=2,则
cos A的值为( )
A. D.3
3.(2023山东威海实验中学期末)如图,一座厂房屋顶人字架的跨度AC=12 m,上弦AB=BC,∠BAC=25°.若用科学计算器求上弦AB的长,则下列按键顺序正确的是( )
A.6×sin25= B.6÷cos25=C.12÷cos25= D.6÷tan25=
4.(2023黑龙江哈尔滨道里二模)关于二次函数y=(x-2)2+3,下列说法正确的是( )
A.函数图象的开口向下
B.函数图象的顶点坐标是(-2,3)
C.当x>2时,y随x的增大而减小
D.该函数图象与y轴的交点坐标是(0,7)
5.(2021山东济宁期末)在△ABC中,∠C,∠B为锐角,且满足=0,则∠A的度数为( )
A.100° B.105° C.90° D.60°
6.(2023河南中考)二次函数y=ax2+bx的图象如图所示,则一次函数y=x+b的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.(2023湖北十堰中考)如图所示,有一天桥高AB为5米,BC是通向天桥的斜坡,∠ACB=45°,市政部门启动“陡改缓”工程,决定将斜坡的底端C延伸到D处,使
∠BDA=30°,则CD的长度约为(参考数据:≈1.414,≈1.732)( )
A.1.59米 B.2.07米 C.3.55米 D.3.66米
8.(2022广西贵港中考)如图,在4×4的正方形网格中,每个小正方形的边长为1,顶点为格点,若△ABC的顶点均在格点处,则cos∠BAC的值是( )
A.
9.【跨学科·物理】(2023陕西靖边二模)物理课上我们学习了物体的竖直上抛运动,若从地面竖直向上抛一小球,小球的高度h(单位:m)与小球运动的时间t(单位:s)之间的函数关系如图所示,下列结论:①小球在空中经过的路程是40 m;②h与t之间的函数关系式为h=(t-3)2+40;③小球的运动时间为6 s;④h=20时,t=1.5.其中正确的有( )
A.1个 B.2个
C.3个 D.4个
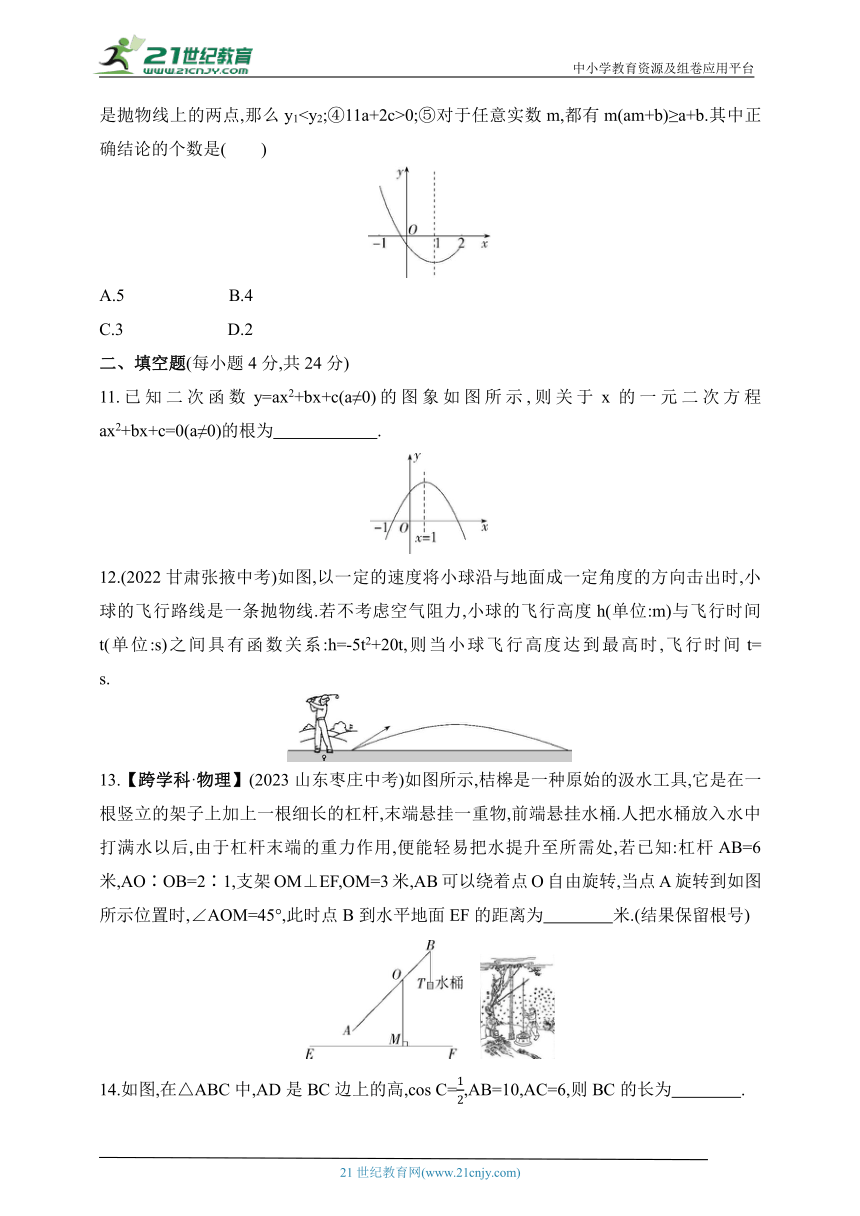
10.(2023山东枣庄中考)二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:①abc<0;②方程ax2+bx+c=0(a≠0)必有一个根大于2且小于3;③如果(0,y1),是抛物线上的两点,那么y10;⑤对于任意实数m,都有m(am+b)≥a+b.其中正确结论的个数是( )
A.5 B.4
C.3 D.2
二、填空题(每小题4分,共24分)
11.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则关于x的一元二次方程ax2+bx+c=0(a≠0)的根为 .
12.(2022甘肃张掖中考)如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系:h=-5t2+20t,则当小球飞行高度达到最高时,飞行时间t= s.
13.【跨学科·物理】(2023山东枣庄中考)如图所示,桔槔是一种原始的汲水工具,它是在一根竖立的架子上加上一根细长的杠杆,末端悬挂一重物,前端悬挂水桶.人把水桶放入水中打满水以后,由于杠杆末端的重力作用,便能轻易把水提升至所需处,若已知:杠杆AB=6米,AO∶OB=2∶1,支架OM⊥EF,OM=3米,AB可以绕着点O自由旋转,当点A旋转到如图所示位置时,∠AOM=45°,此时点B到水平地面EF的距离为 米.(结果保留根号)
14.如图,在△ABC中,AD是BC边上的高,cos C=,AB=10,AC=6,则BC的长为 .
15.(2022江苏常州中考)如图,在四边形ABCD中,∠A=∠ABC=90°,DB平分
∠ADC.若AD=1,CD=3,则sin∠ABD= .
16.如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的,正常水位时,大孔水面宽度AB为20 m,顶点M距水面6 m(即MO=6 m),小孔顶点N距水面4.5 m(即NC=4.5 m),建立如图所示的平面直角坐标系.当水位上涨到刚好淹没小孔时,大孔的水面宽度EF= m.
三、解答题(共66分)
17.[含评分细则](8分)计算:
(1)2sin 30°-3tan 45°·sin 45°+4cos 60°;
(2)+cos 45°·sin 60°.
18.[含评分细则](2023广东东莞期中)(6分)如图,在△ABC中,AB=2,∠B=60°,
∠C=45°,求BC和AC的长.
19.[含评分细则](2022山东青岛中考)(8分)已知二次函数y=x2+mx+m2-3(m为常数,m>0)的图象经过点P(2,4).
(1)求m的值;
(2)判断二次函数y=x2+mx+m2-3的图象与x轴交点的个数,并说明理由.
20.[含评分细则]【项目式学习试题】(2023山西中考)(8分)2023年3月,水利部印发《母亲河复苏行动河湖名单(2022—2025年)》,我省境内有汾河、桑干河、洋河、清漳河、浊漳河、沁河六条河流入选.在推进实施母亲河复苏行动中,需要砌筑各种驳岸(也叫护坡).某校“综合与实践”小组的同学把“母亲河驳岸的调研与计算”作为一项课题活动,利用课余时间完成了实践调查,并形成了如下活动报告.请根据活动报告计算BC和AB的长度(结果精确到0.1 m.参考数据:
≈1.73,≈1.41).
课题 母亲河驳岸的调研与计算
调查方式 资料查阅、水利部门走访、实地查看了解
调查内容 功能 驳岸是用来保护河岸,阻止河岸崩塌或冲刷的构筑物
材料 所需材料为石料、混凝土等
驳岸 剖面图
相关数据 及说明 图中,点A,B,C,D,E在同一竖直平面内,AE和CD均与地面平行,岸墙AB⊥AE于点A,∠BCD=135°,∠EDC= 60°,ED=6 m,AE=1.5 m,CD=3.5 m
计算结果 …
交流 展示 …
21.[含评分细则](2023浙江杭州中考)(12分)设二次函数y=ax2+bx+1(a≠0,b是实数).已知函数值y和自变量x的部分对应取值如下表所示:
x … -1 0 1 2 3 …
y … m 1 n 1 p …
(1)若m=4,
①求二次函数的表达式;
②写出一个符合条件的x的取值范围,使得y随x的增大而减小.
(2)若在m,n,p这三个实数中,只有一个是正数,求a的取值范围.
22.[含评分细则]【新素材】(2023湖北孝感中考)(12分)加强劳动教育,落实五育并举.孝礼中学在当地政府的支持下,建成了一处劳动实践基地.2023年计划将其中1 000 m2的土地全部种植甲、乙两种蔬菜.经调查发现:甲种蔬菜种植成本y(单位:元/m2)与其种植面积x(单位:m2)的函数关系如图所示,其中200≤x≤700;乙种蔬菜的种植成本为50元/m2.
(1)当x= 时,y=35.
(2)设2023年甲、乙两种蔬菜总种植成本为W元,如何分配两种蔬菜的种植面积,使W最小
(3)学校计划今后每年在这1 000 m2土地上,均按(2)中方案种植蔬菜,因技术改进,预计种植成本逐年下降.若甲种蔬菜种植成本平均每年下降10%,乙种蔬菜种植成本平均每年下降a%,当a为何值时,2025年的总种植成本为28 920元
23.[含评分细则](2022江苏连云港中考)(12分)已知二次函数y=x2+(m-2)x+m-4,其中m>2.
(1)当该函数的图象经过原点O(0,0)时,求此函数图象的顶点A的坐标;
(2)求证:二次函数y=x2+(m-2)x+m-4的图象的顶点在第三象限;
(3)如图,在(1)的条件下,若平移该二次函数的图象,使其顶点在直线y=-x-2上运动,平移后所得函数的图象与y轴的负半轴的交点为B,求△AOB面积的最大值.
答案全解全析
1.B A.y=x+是一次函数,不是二次函数,故本选项不符合题意;B.y=3(x-1)2是二次函数,故本选项符合题意;C.当a=0时,y=ax2+bx+c不是二次函数,故本选项不符合题意;D.y=+3x中的不是整式,不是二次函数,故本选项不符合题意.故选B.
2.B 在直角△ABC中,AB=,则cos A=.故选B.
3.B 过B点作BD⊥AC于D,∵AB=BC,BD⊥AC,AC=12米,∴AD=CD=6米,在Rt△ADB中,∠BAC=25°,∴AB=米,故按键顺序正确的是6÷cos25=.故选B.
4.D ∵二次函数y=(x-2)2+3中,a=1>0,∴图象的开口向上,A错误;函数图象的顶点坐标是(2,3),B错误;当x>2时,y随x的增大而增大,C错误;令y=(x-2)2+3中的x=0,解得y=7,∴函数图象与y轴的交点坐标是(0,7),D正确.故选D.
5.B ∵=0,∴sin C=,cos B=,∵∠C,∠B为锐角,
∴∠C=45°,∠B=30°,∴∠A的度数为180°-45°-30°=105°.故选B.
6.D 由函数图象可得a<0,->0,∴b>0,∴y=x+b的图象过第一、二、三象限,不过第四象限,故选D.
7.D 在Rt△ABC中,∠BAC=90°,∠ACB=45°,
∴∠ABC=∠ACB=45°,∴AC=AB=5米,
在Rt△ABD中,∠BAD=90°,∠BDA=30°,
∴AD=米,
∴CD=AD-AC=5-5≈1.732×5-5=3.66(米),∴CD的长度约为3.66米,故选D.
8.C 延长AC到D,连接BD,如图,
∵AD2=22+42=20,BD2=12+22=5,AB2=32+42=25,
∴AD2+BD2=AB2,∴∠ADB=90°,
∴cos∠BAC=,故选C.
9.A 由图象知,小球在空中达到的最大高度是40 m,故①错误;设函数解析式为h=a(t-3)2+40,由题意得a(0-3)2+40=0,解得a=-(t-3)2+40,故②错误;由图象可知,小球6 s时落地,故小球运动的时间为6 s,故③正确;当h=20时,
-(t-3)2+40=20,解得t=,故④错误.故选A.
10.C ①根据图象可知a>0,c<0,∵对称轴是直线x=1,∴-=1,即b=-2a,∴b<0,
∴abc>0,故①错误.②方程ax2+bx+c=0的根即为二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点横坐标,根据图象已知一个交点的横坐标x1满足-1,∴点离对称轴更近,∴y1>y2,故③错误.④根据图象可知,当x=-1时,y=a-b+c=a+2a+c=3a+c>0,∴6a+2c>0,∵a>0,∴5a+6a+2c>0,即11a+
2c>0,故④正确.⑤观察图象可知,当x=1时,y有最小值a+b+c,∴am2+bm+c≥a+b+c,即m(am+b)≥a+b,故⑤正确.综上,②④⑤正确,故选C.
11.x1=-1,x2=3
解析 根据图象知,抛物线y=ax2+bx+c(a≠0)与x轴的一个交点是(-1,0),对称轴是直线x=1,
∴抛物线与x轴的另一个交点是(3,0).
∴关于x的一元二次方程ax2+bx+c=0(a≠0)的根为x1=-1,x2=3.
12.2
解析 ∵h=-5t2+20t=-5(t-2)2+20,且-5<0,∴当t=2时,h取得最大值,故答案为2.
13.(3+)
解析 过点O作OC⊥BT,垂足为C,
由题意得BC∥OM,
∴∠AOM=∠OBC=45°,
∵AB=6米,AO∶OB=2∶1,∴AO=4米,OB=2米,
在Rt△OBC中,BC=OB·cos 45°=2×(米),
∵OM=3米,∴此时点B到水平地面EF的距离=BC+OM=(3+)米,
故答案为(3+).
14.3+
解析 ∵AD是BC边上的高,∴∠ADC=90°,
∵cos C=×6=3,
∴AD=.
在Rt△ADB中,BD=,
∴BC=CD+BD=3+.
15.
解析 过点D作DE⊥BC,垂足为E,如图,
∵∠A=∠ABC=90°,∴AD∥BC,∴∠ADB=∠CBD,
∵DB平分∠ADC,∴∠ADB=∠CDB,∴∠CBD=∠CDB,∴CB=CD=3,
易知AD=BE=1,∴CE=BC-BE=3-1=2,
在Rt△CDE中,DE=,易知AB=DE=,
在Rt△ADB中,BD=,
∴sin∠ABD=.
16.10
解析 由题意得,M点坐标为(0,6),A点坐标为(-10,0),B点坐标为(10,0),设中间大抛物线的函数解析式为y=ax2+bx+c,代入三点的坐标得到∴函数的解析式为y=-x2+6.令y=4.5,则-x2+6=4.5,解得x1=5,
x2=-5,∴EF=5-(-5)=10(米).
17.解析 (1)2sin 30°-3tan 45°·sin 45°+4cos 60°=2×.4分
(2)+cos 45°·sin 60°=.8分
18.解析 过点A作AD⊥BC于D,则∠ADB=90°,1分
∵∠B=60°,∴∠BAD=30°,∴BD=×2=1,
∴AD=,3分
∵∠C=45°,∴AD=CD=,4分
∴AC=,5分
BC=BD+CD=1+.6分
19.解析 (1)将(2,4)代入y=x2+mx+m2-3,得4=4+2m+m2-3,解得m1=1,m2=-3,
又∵m>0,∴m=1.4分
(2)二次函数y=x2+mx+m2-3的图象与x轴有两个交点.理由如下:
∵m=1,∴y=x2+x-2,∵b2-4ac=12+8=9>0,
∴二次函数图象与x轴有两个交点.8分
20.解析 如图,过E作EF⊥CD于F,延长AB,DC交于H,∴∠EFD=90°,
在Rt△EFD中,∵∠EDF=60°,ED=6 m,sin∠EDF=,cos∠EDF=,
∴EF=ED·sin∠EDF=6×sin 60°=6×(m),
FD=ED·cos∠EDF=6×cos 60°=6×=3(m),2分
由题意得∠H=90°,四边形AEFH是矩形,
∴AH=EF=3 m,HF=AE=1.5 m,4分
∵CF=CD-FD=3.5-3=0.5(m),∴CH=HF-CF=1.5-0.5=1(m),
在Rt△BCH中,∠H=90°,∠BCH=180°-∠BCD=180°-135°=45°,cos∠BCH=,tan∠BCH=,∴BC=≈1.4(m),6分
BH=CH·tan∠BCH=1×tan 45°=1(m),
∴AB=AH-BH=3-1≈4.2(m).
答:BC的长度约为1.4 m,AB的长度约为4.2 m.8分
21.解析 (1)①由题意得
∴二次函数的表达式是y=x2-2x+1.3分
②∵y=x2-2x+1=(x-1)2,∴抛物线开口向上,对称轴为直线x=1,
∴当x<1时,y随x的增大而减小.6分
(答案不唯一,合理即可)
(2)∵x=0和x=2时的函数值都是1,∴抛物线的对称轴为直线x=-=1,
∴点(1,n)是顶点,点(-1,m)和点(3,p)关于对称轴对称,8分
若在m,n,p这三个实数中,只有一个是正数,则n>0,m=p≤0,10分
∵-=1,∴b=-2a,∴二次函数为y=ax2-2ax+1,
∴m=a+2a+1≤0,a-2a+1>0,∴a≤-.12分
22.解析 (1)500.2分
详解:当200≤x≤600时,设甲种蔬菜种植成本y(单位:元/m2)与其种植面积x(单位:m2)的函数关系式为y=kx+b,把(200,20),(600,40)代入得x+10,当600(2)当200≤x≤600时,W=x+50(1 000-x)=(x-400)2+42 000,
∵>0,∴抛物线开口向上,
∴当x=400时,W有最小值,最小值为42 000,
此时1 000-x=1 000-400=600.4分
当600∵-10<0,∴W随x的增大而减小,
∴当x=700时,W有最小值,为-10×700+50 000=43 000.6分
∵42 000<43 000,
∴当甲种蔬菜的种植面积为400 m2,乙种蔬菜的种植面积为600 m2时,W最小.7分
(3)由(2)可知,甲、乙两种蔬菜总种植成本为42 000元,乙种蔬菜的种植成本为50×600=30 000(元),则甲种蔬菜的种植成本为42 000-30 000=12 000(元),9分
由题意得12 000×(1-10%)2+30 000(1-a%)2=28 920,10分
设a%=m,整理得(1-m)2=0.64,解得m1=0.2=20%,m2=1.8(不符合题意,舍去),
∴a%=20%,∴a=20.
答:当a的值为20时,2025年的总种植成本为28 920元.12分
23.解析 (1)把O(0,0)代入y=x2+(m-2)x+m-4得m-4=0,解得m=4,
∴y=x2+2x=(x+1)2-1,∴函数图象的顶点A的坐标为(-1,-1).3分
(2)证明:由抛物线顶点坐标公式得抛物线y=x2+(m-2)x+m-4的顶点坐标为,4分
∵m>2,∴2-m<0,∴(m-4)2-1≤-1<0,
∴二次函数y=x2+(m-2)x+m-4的图象的顶点在第三象限.7分
(3)设平移后图象对应的二次函数表达式为y=x2+bx+c,其顶点坐标为,
当x=0时,y=x2+bx+c=c,∴B(0,c),将代入y=-x-2得-2,
∴c=,∵B(0,c)在y轴的负半轴上,∴c<0,
∴OB=-c=-,9分
过点A作AH⊥OB于H,如图:
∵A(-1,-1),∴AH=1,
∴S△AOB=OB·AH=,
∵-<0,∴当b=-1时(此时c<0),S△AOB取得最大值,最大值为.
故△AOB面积的最大值是.12分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师大版数学九年级下学期
期中素养综合测试
(满分120分,限时100分钟)
一、选择题(每小题3分,共30分)
1.(2023辽宁鞍山立山一模)下列函数是二次函数的是( )
A.y=x+ B.y=3(x-1)2
C.y=ax2+bx+c D.y=+3x
2.(2023黑龙江哈尔滨平房二模)如图,在Rt△ABC中,∠C=90°,AC=6,BC=2,则
cos A的值为( )
A. D.3
3.(2023山东威海实验中学期末)如图,一座厂房屋顶人字架的跨度AC=12 m,上弦AB=BC,∠BAC=25°.若用科学计算器求上弦AB的长,则下列按键顺序正确的是( )
A.6×sin25= B.6÷cos25=C.12÷cos25= D.6÷tan25=
4.(2023黑龙江哈尔滨道里二模)关于二次函数y=(x-2)2+3,下列说法正确的是( )
A.函数图象的开口向下
B.函数图象的顶点坐标是(-2,3)
C.当x>2时,y随x的增大而减小
D.该函数图象与y轴的交点坐标是(0,7)
5.(2021山东济宁期末)在△ABC中,∠C,∠B为锐角,且满足=0,则∠A的度数为( )
A.100° B.105° C.90° D.60°
6.(2023河南中考)二次函数y=ax2+bx的图象如图所示,则一次函数y=x+b的图象一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.(2023湖北十堰中考)如图所示,有一天桥高AB为5米,BC是通向天桥的斜坡,∠ACB=45°,市政部门启动“陡改缓”工程,决定将斜坡的底端C延伸到D处,使
∠BDA=30°,则CD的长度约为(参考数据:≈1.414,≈1.732)( )
A.1.59米 B.2.07米 C.3.55米 D.3.66米
8.(2022广西贵港中考)如图,在4×4的正方形网格中,每个小正方形的边长为1,顶点为格点,若△ABC的顶点均在格点处,则cos∠BAC的值是( )
A.
9.【跨学科·物理】(2023陕西靖边二模)物理课上我们学习了物体的竖直上抛运动,若从地面竖直向上抛一小球,小球的高度h(单位:m)与小球运动的时间t(单位:s)之间的函数关系如图所示,下列结论:①小球在空中经过的路程是40 m;②h与t之间的函数关系式为h=(t-3)2+40;③小球的运动时间为6 s;④h=20时,t=1.5.其中正确的有( )
A.1个 B.2个
C.3个 D.4个
10.(2023山东枣庄中考)二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,下列结论:①abc<0;②方程ax2+bx+c=0(a≠0)必有一个根大于2且小于3;③如果(0,y1),是抛物线上的两点,那么y1
A.5 B.4
C.3 D.2
二、填空题(每小题4分,共24分)
11.已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则关于x的一元二次方程ax2+bx+c=0(a≠0)的根为 .
12.(2022甘肃张掖中考)如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系:h=-5t2+20t,则当小球飞行高度达到最高时,飞行时间t= s.
13.【跨学科·物理】(2023山东枣庄中考)如图所示,桔槔是一种原始的汲水工具,它是在一根竖立的架子上加上一根细长的杠杆,末端悬挂一重物,前端悬挂水桶.人把水桶放入水中打满水以后,由于杠杆末端的重力作用,便能轻易把水提升至所需处,若已知:杠杆AB=6米,AO∶OB=2∶1,支架OM⊥EF,OM=3米,AB可以绕着点O自由旋转,当点A旋转到如图所示位置时,∠AOM=45°,此时点B到水平地面EF的距离为 米.(结果保留根号)
14.如图,在△ABC中,AD是BC边上的高,cos C=,AB=10,AC=6,则BC的长为 .
15.(2022江苏常州中考)如图,在四边形ABCD中,∠A=∠ABC=90°,DB平分
∠ADC.若AD=1,CD=3,则sin∠ABD= .
16.如图,三孔桥横截面的三个孔都呈抛物线形,左右两个抛物线形是全等的,正常水位时,大孔水面宽度AB为20 m,顶点M距水面6 m(即MO=6 m),小孔顶点N距水面4.5 m(即NC=4.5 m),建立如图所示的平面直角坐标系.当水位上涨到刚好淹没小孔时,大孔的水面宽度EF= m.
三、解答题(共66分)
17.[含评分细则](8分)计算:
(1)2sin 30°-3tan 45°·sin 45°+4cos 60°;
(2)+cos 45°·sin 60°.
18.[含评分细则](2023广东东莞期中)(6分)如图,在△ABC中,AB=2,∠B=60°,
∠C=45°,求BC和AC的长.
19.[含评分细则](2022山东青岛中考)(8分)已知二次函数y=x2+mx+m2-3(m为常数,m>0)的图象经过点P(2,4).
(1)求m的值;
(2)判断二次函数y=x2+mx+m2-3的图象与x轴交点的个数,并说明理由.
20.[含评分细则]【项目式学习试题】(2023山西中考)(8分)2023年3月,水利部印发《母亲河复苏行动河湖名单(2022—2025年)》,我省境内有汾河、桑干河、洋河、清漳河、浊漳河、沁河六条河流入选.在推进实施母亲河复苏行动中,需要砌筑各种驳岸(也叫护坡).某校“综合与实践”小组的同学把“母亲河驳岸的调研与计算”作为一项课题活动,利用课余时间完成了实践调查,并形成了如下活动报告.请根据活动报告计算BC和AB的长度(结果精确到0.1 m.参考数据:
≈1.73,≈1.41).
课题 母亲河驳岸的调研与计算
调查方式 资料查阅、水利部门走访、实地查看了解
调查内容 功能 驳岸是用来保护河岸,阻止河岸崩塌或冲刷的构筑物
材料 所需材料为石料、混凝土等
驳岸 剖面图
相关数据 及说明 图中,点A,B,C,D,E在同一竖直平面内,AE和CD均与地面平行,岸墙AB⊥AE于点A,∠BCD=135°,∠EDC= 60°,ED=6 m,AE=1.5 m,CD=3.5 m
计算结果 …
交流 展示 …
21.[含评分细则](2023浙江杭州中考)(12分)设二次函数y=ax2+bx+1(a≠0,b是实数).已知函数值y和自变量x的部分对应取值如下表所示:
x … -1 0 1 2 3 …
y … m 1 n 1 p …
(1)若m=4,
①求二次函数的表达式;
②写出一个符合条件的x的取值范围,使得y随x的增大而减小.
(2)若在m,n,p这三个实数中,只有一个是正数,求a的取值范围.
22.[含评分细则]【新素材】(2023湖北孝感中考)(12分)加强劳动教育,落实五育并举.孝礼中学在当地政府的支持下,建成了一处劳动实践基地.2023年计划将其中1 000 m2的土地全部种植甲、乙两种蔬菜.经调查发现:甲种蔬菜种植成本y(单位:元/m2)与其种植面积x(单位:m2)的函数关系如图所示,其中200≤x≤700;乙种蔬菜的种植成本为50元/m2.
(1)当x= 时,y=35.
(2)设2023年甲、乙两种蔬菜总种植成本为W元,如何分配两种蔬菜的种植面积,使W最小
(3)学校计划今后每年在这1 000 m2土地上,均按(2)中方案种植蔬菜,因技术改进,预计种植成本逐年下降.若甲种蔬菜种植成本平均每年下降10%,乙种蔬菜种植成本平均每年下降a%,当a为何值时,2025年的总种植成本为28 920元
23.[含评分细则](2022江苏连云港中考)(12分)已知二次函数y=x2+(m-2)x+m-4,其中m>2.
(1)当该函数的图象经过原点O(0,0)时,求此函数图象的顶点A的坐标;
(2)求证:二次函数y=x2+(m-2)x+m-4的图象的顶点在第三象限;
(3)如图,在(1)的条件下,若平移该二次函数的图象,使其顶点在直线y=-x-2上运动,平移后所得函数的图象与y轴的负半轴的交点为B,求△AOB面积的最大值.
答案全解全析
1.B A.y=x+是一次函数,不是二次函数,故本选项不符合题意;B.y=3(x-1)2是二次函数,故本选项符合题意;C.当a=0时,y=ax2+bx+c不是二次函数,故本选项不符合题意;D.y=+3x中的不是整式,不是二次函数,故本选项不符合题意.故选B.
2.B 在直角△ABC中,AB=,则cos A=.故选B.
3.B 过B点作BD⊥AC于D,∵AB=BC,BD⊥AC,AC=12米,∴AD=CD=6米,在Rt△ADB中,∠BAC=25°,∴AB=米,故按键顺序正确的是6÷cos25=.故选B.
4.D ∵二次函数y=(x-2)2+3中,a=1>0,∴图象的开口向上,A错误;函数图象的顶点坐标是(2,3),B错误;当x>2时,y随x的增大而增大,C错误;令y=(x-2)2+3中的x=0,解得y=7,∴函数图象与y轴的交点坐标是(0,7),D正确.故选D.
5.B ∵=0,∴sin C=,cos B=,∵∠C,∠B为锐角,
∴∠C=45°,∠B=30°,∴∠A的度数为180°-45°-30°=105°.故选B.
6.D 由函数图象可得a<0,->0,∴b>0,∴y=x+b的图象过第一、二、三象限,不过第四象限,故选D.
7.D 在Rt△ABC中,∠BAC=90°,∠ACB=45°,
∴∠ABC=∠ACB=45°,∴AC=AB=5米,
在Rt△ABD中,∠BAD=90°,∠BDA=30°,
∴AD=米,
∴CD=AD-AC=5-5≈1.732×5-5=3.66(米),∴CD的长度约为3.66米,故选D.
8.C 延长AC到D,连接BD,如图,
∵AD2=22+42=20,BD2=12+22=5,AB2=32+42=25,
∴AD2+BD2=AB2,∴∠ADB=90°,
∴cos∠BAC=,故选C.
9.A 由图象知,小球在空中达到的最大高度是40 m,故①错误;设函数解析式为h=a(t-3)2+40,由题意得a(0-3)2+40=0,解得a=-(t-3)2+40,故②错误;由图象可知,小球6 s时落地,故小球运动的时间为6 s,故③正确;当h=20时,
-(t-3)2+40=20,解得t=,故④错误.故选A.
10.C ①根据图象可知a>0,c<0,∵对称轴是直线x=1,∴-=1,即b=-2a,∴b<0,
∴abc>0,故①错误.②方程ax2+bx+c=0的根即为二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点横坐标,根据图象已知一个交点的横坐标x1满足-1
2c>0,故④正确.⑤观察图象可知,当x=1时,y有最小值a+b+c,∴am2+bm+c≥a+b+c,即m(am+b)≥a+b,故⑤正确.综上,②④⑤正确,故选C.
11.x1=-1,x2=3
解析 根据图象知,抛物线y=ax2+bx+c(a≠0)与x轴的一个交点是(-1,0),对称轴是直线x=1,
∴抛物线与x轴的另一个交点是(3,0).
∴关于x的一元二次方程ax2+bx+c=0(a≠0)的根为x1=-1,x2=3.
12.2
解析 ∵h=-5t2+20t=-5(t-2)2+20,且-5<0,∴当t=2时,h取得最大值,故答案为2.
13.(3+)
解析 过点O作OC⊥BT,垂足为C,
由题意得BC∥OM,
∴∠AOM=∠OBC=45°,
∵AB=6米,AO∶OB=2∶1,∴AO=4米,OB=2米,
在Rt△OBC中,BC=OB·cos 45°=2×(米),
∵OM=3米,∴此时点B到水平地面EF的距离=BC+OM=(3+)米,
故答案为(3+).
14.3+
解析 ∵AD是BC边上的高,∴∠ADC=90°,
∵cos C=×6=3,
∴AD=.
在Rt△ADB中,BD=,
∴BC=CD+BD=3+.
15.
解析 过点D作DE⊥BC,垂足为E,如图,
∵∠A=∠ABC=90°,∴AD∥BC,∴∠ADB=∠CBD,
∵DB平分∠ADC,∴∠ADB=∠CDB,∴∠CBD=∠CDB,∴CB=CD=3,
易知AD=BE=1,∴CE=BC-BE=3-1=2,
在Rt△CDE中,DE=,易知AB=DE=,
在Rt△ADB中,BD=,
∴sin∠ABD=.
16.10
解析 由题意得,M点坐标为(0,6),A点坐标为(-10,0),B点坐标为(10,0),设中间大抛物线的函数解析式为y=ax2+bx+c,代入三点的坐标得到∴函数的解析式为y=-x2+6.令y=4.5,则-x2+6=4.5,解得x1=5,
x2=-5,∴EF=5-(-5)=10(米).
17.解析 (1)2sin 30°-3tan 45°·sin 45°+4cos 60°=2×.4分
(2)+cos 45°·sin 60°=.8分
18.解析 过点A作AD⊥BC于D,则∠ADB=90°,1分
∵∠B=60°,∴∠BAD=30°,∴BD=×2=1,
∴AD=,3分
∵∠C=45°,∴AD=CD=,4分
∴AC=,5分
BC=BD+CD=1+.6分
19.解析 (1)将(2,4)代入y=x2+mx+m2-3,得4=4+2m+m2-3,解得m1=1,m2=-3,
又∵m>0,∴m=1.4分
(2)二次函数y=x2+mx+m2-3的图象与x轴有两个交点.理由如下:
∵m=1,∴y=x2+x-2,∵b2-4ac=12+8=9>0,
∴二次函数图象与x轴有两个交点.8分
20.解析 如图,过E作EF⊥CD于F,延长AB,DC交于H,∴∠EFD=90°,
在Rt△EFD中,∵∠EDF=60°,ED=6 m,sin∠EDF=,cos∠EDF=,
∴EF=ED·sin∠EDF=6×sin 60°=6×(m),
FD=ED·cos∠EDF=6×cos 60°=6×=3(m),2分
由题意得∠H=90°,四边形AEFH是矩形,
∴AH=EF=3 m,HF=AE=1.5 m,4分
∵CF=CD-FD=3.5-3=0.5(m),∴CH=HF-CF=1.5-0.5=1(m),
在Rt△BCH中,∠H=90°,∠BCH=180°-∠BCD=180°-135°=45°,cos∠BCH=,tan∠BCH=,∴BC=≈1.4(m),6分
BH=CH·tan∠BCH=1×tan 45°=1(m),
∴AB=AH-BH=3-1≈4.2(m).
答:BC的长度约为1.4 m,AB的长度约为4.2 m.8分
21.解析 (1)①由题意得
∴二次函数的表达式是y=x2-2x+1.3分
②∵y=x2-2x+1=(x-1)2,∴抛物线开口向上,对称轴为直线x=1,
∴当x<1时,y随x的增大而减小.6分
(答案不唯一,合理即可)
(2)∵x=0和x=2时的函数值都是1,∴抛物线的对称轴为直线x=-=1,
∴点(1,n)是顶点,点(-1,m)和点(3,p)关于对称轴对称,8分
若在m,n,p这三个实数中,只有一个是正数,则n>0,m=p≤0,10分
∵-=1,∴b=-2a,∴二次函数为y=ax2-2ax+1,
∴m=a+2a+1≤0,a-2a+1>0,∴a≤-.12分
22.解析 (1)500.2分
详解:当200≤x≤600时,设甲种蔬菜种植成本y(单位:元/m2)与其种植面积x(单位:m2)的函数关系式为y=kx+b,把(200,20),(600,40)代入得x+10,当600
∵>0,∴抛物线开口向上,
∴当x=400时,W有最小值,最小值为42 000,
此时1 000-x=1 000-400=600.4分
当600
∴当x=700时,W有最小值,为-10×700+50 000=43 000.6分
∵42 000<43 000,
∴当甲种蔬菜的种植面积为400 m2,乙种蔬菜的种植面积为600 m2时,W最小.7分
(3)由(2)可知,甲、乙两种蔬菜总种植成本为42 000元,乙种蔬菜的种植成本为50×600=30 000(元),则甲种蔬菜的种植成本为42 000-30 000=12 000(元),9分
由题意得12 000×(1-10%)2+30 000(1-a%)2=28 920,10分
设a%=m,整理得(1-m)2=0.64,解得m1=0.2=20%,m2=1.8(不符合题意,舍去),
∴a%=20%,∴a=20.
答:当a的值为20时,2025年的总种植成本为28 920元.12分
23.解析 (1)把O(0,0)代入y=x2+(m-2)x+m-4得m-4=0,解得m=4,
∴y=x2+2x=(x+1)2-1,∴函数图象的顶点A的坐标为(-1,-1).3分
(2)证明:由抛物线顶点坐标公式得抛物线y=x2+(m-2)x+m-4的顶点坐标为,4分
∵m>2,∴2-m<0,∴(m-4)2-1≤-1<0,
∴二次函数y=x2+(m-2)x+m-4的图象的顶点在第三象限.7分
(3)设平移后图象对应的二次函数表达式为y=x2+bx+c,其顶点坐标为,
当x=0时,y=x2+bx+c=c,∴B(0,c),将代入y=-x-2得-2,
∴c=,∵B(0,c)在y轴的负半轴上,∴c<0,
∴OB=-c=-,9分
过点A作AH⊥OB于H,如图:
∵A(-1,-1),∴AH=1,
∴S△AOB=OB·AH=,
∵-<0,∴当b=-1时(此时c<0),S△AOB取得最大值,最大值为.
故△AOB面积的最大值是.12分
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
