2024北师大版数学九年级下学期课时练--专项素养综合全练(九)数学文化与新定义型试题(含解析)
文档属性
| 名称 | 2024北师大版数学九年级下学期课时练--专项素养综合全练(九)数学文化与新定义型试题(含解析) | 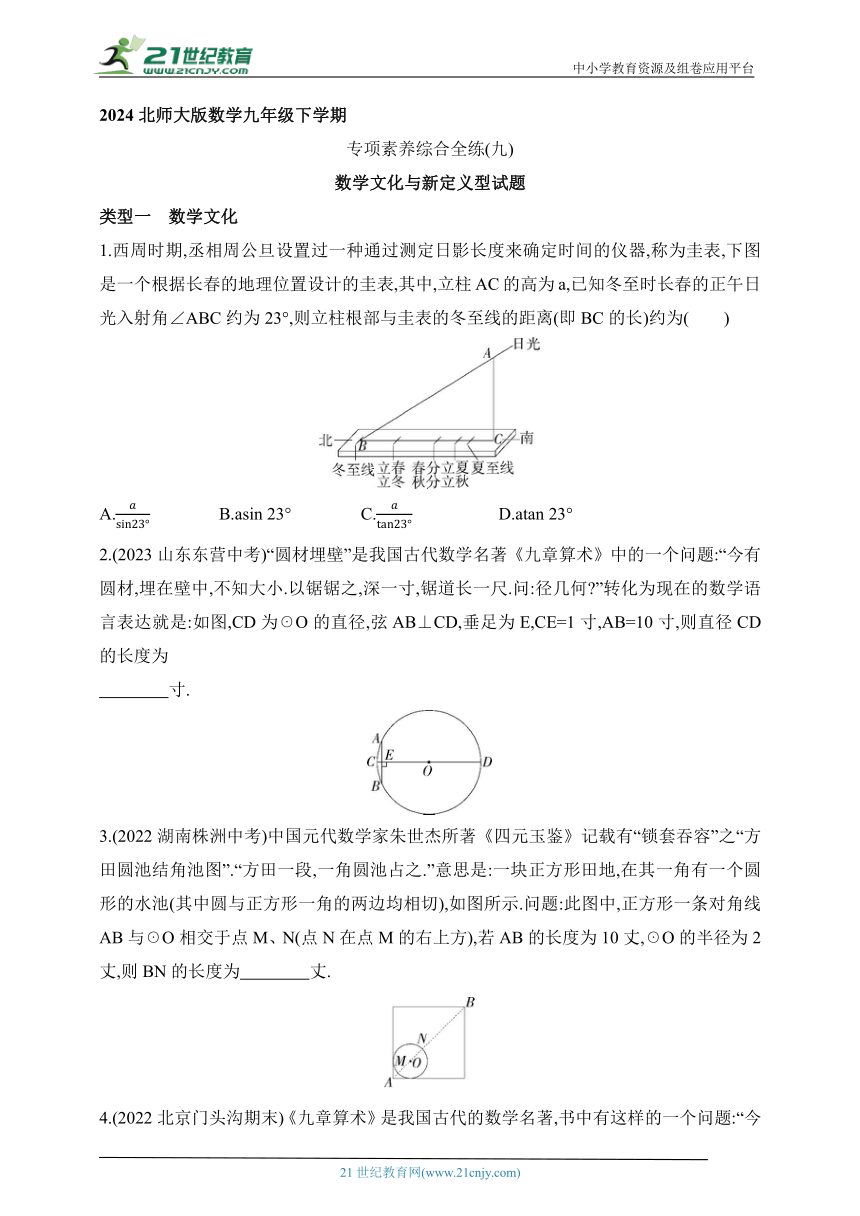 | |
| 格式 | docx | ||
| 文件大小 | 443.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-11-28 21:11:59 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024北师大版数学九年级下学期
专项素养综合全练(九)
数学文化与新定义型试题
类型一 数学文化
1.西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表,下图是一个根据长春的地理位置设计的圭表,其中,立柱AC的高为a,已知冬至时长春的正午日光入射角∠ABC约为23°,则立柱根部与圭表的冬至线的距离(即BC的长)约为( )
A. B.asin 23° C. D.atan 23°
2.(2023山东东营中考)“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问:径几何 ”转化为现在的数学语言表达就是:如图,CD为☉O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=10寸,则直径CD的长度为
寸.
3.(2022湖南株洲中考)中国元代数学家朱世杰所著《四元玉鉴》记载有“锁套吞容”之“方田圆池结角池图”.“方田一段,一角圆池占之.”意思是:一块正方形田地,在其一角有一个圆形的水池(其中圆与正方形一角的两边均相切),如图所示.问题:此图中,正方形一条对角线AB与☉O相交于点M、N(点N在点M的右上方),若AB的长度为10丈,☉O的半径为2丈,则BN的长度为 丈.
4.(2022北京门头沟期末)《九章算术》是我国古代的数学名著,书中有这样的一个问题:“今有勾八步,股十五步,问勾中容圆径几何 ”其意思是:如图,现有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问:该直角三角形所能容纳的最大圆的直径是多少
答:该直角三角形所能容纳的最大圆的直径是 步.
5.(2020湖南株洲中考)据《汉书·律历志》记载:“量者,龠(yuè)、合、升、斗、斛(hú)也.”斛是中国古代的一种量器.“斛底,方而圜(huán)其外,旁有庣(tiāo)焉.”意思是:斛的底面为正方形外接一个圆,此圆外是一个同心圆,如图所示.问题:现有一斛,其底面的外圆直径为两尺五寸(即2.5尺),“庣旁”为两寸五分(即两同心圆的外圆与内圆的半径之差为0.25尺),则此斛底面的正方形的周长为 尺.(结果用最简根式表示)
类型二 新定义型试题
6.如图,在△ABC中,∠C=90°,定义:斜边与∠A的邻边的比叫做∠A的正割,用“sec A”表示,若设该直角三角形的各边分别为a,b,c,则sec A=,下列选项正确的是( )
A.sec B·sin A=1 B.sec B= C.sec A·cos B=1 D.sec2A·sec2B=1
7.(2022黑龙江绥化中考)定义一种运算:
sin(α+β)=sin αcos β+cos αsin β,sin(α-β)=sin αcos β-cos αsin β.
例如:当α=45°,β=30°时,sin(45°+30°)=,则
sin 15°的值为 .
8.(2023四川巴中中考)规定:如果两个函数的图象关于y轴对称,那么称这两个函数互为“Y函数”.例如:函数y=x+3与y=-x+3互为“Y函数”.若函数y=x2+(k-1)x+k-3的图象与x轴只有一个交点,则它的“Y函数”图象与x轴的交点坐标为 .
9.(2023四川自贡沿滩月考)我们定义一种新函数:形如y=|ax2+bx+c|(a
≠0,b2-4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=
|x2-2x-3|的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为(-1,0),(3,0)和(0,3);②图象具有对称性,对称轴是直线x=1;③当-1≤
x≤1或x≥3时,函数值y随x值的增大而增大;④当x=-1或x=3时,函数有最小值,是0;⑤当x=1时,函数有最大值,是4.其中正确的结论有
.(填正确的序号)
10.(2022湖北鄂州中考节选)某数学兴趣小组运用《几何画板》软件探究y=ax2(a>0)的图象.发现:如图1所示,该类型图象上任意一点M到定点F的距离MF,始终等于它到定直线l:y=-的距离MN
(该结论不需要证明),他们称:定点F为图象的焦点,定直线l为图象的准线,y=-叫做抛物线的准线方程.其中原点O为FH的中点,FH=
2OF=.例如:抛物线y=x2,其焦点坐标为F,准线方程为l:y=-.其中MF=MN,FH=2OF=1.
【基础训练】(1)请分别直接写出抛物线y=2x2的焦点坐标和准线l的方程: , .
【技能训练】(2)如图2所示,已知抛物线y=x2上一点P到准线l的距离为6,求点P的坐标.
【能力提升】(3)如图3所示,已知过抛物线y=ax2(a>0)的焦点F的直线依次交抛物线及准线l于点A、B、C.若BC=2BF,AF=4,求a的值.
图1 图2 图3
答案全解全析
1.C 由题意可得,立柱根部与圭表的冬至线的距离为,故选C.
2.26
解析 连接OA,设☉O的半径是r寸,
∵直径CD⊥AB,∴AE=×10=5寸,
∵CE=1寸,∴OE=(r-1)寸,
∵OA2=OE2+AE2,∴r2=(r-1)2+52,∴r=13,
∴直径CD的长度为2×13=26寸.故答案为26.
3.(8-2)
解析 根据题意易知圆心O在AB上,如图,设正方形的一边与☉O的切点为C,连接OC,则OC⊥AC,
∵四边形是正方形,AB是对角线,∴∠OAC=45°,
∴OA=(丈),
∴BN=AB-AN=10-(2)丈,
故答案为(8-2).
4.6
解析 如图:
在Rt△ABC中,AC=8步,BC=15步,∠ACB=90°,
∴AB==17步,
S△ABC=AC·BC=×8×15=60(步2),
设内切圆的圆心为O,分别连接圆心和三个切点,及OA、OB、OC,
设内切圆的半径为r步,
∴S△ABC=S△AOB+S△BOC+S△AOC=r·(AB+BC+AC)=20r(步2),
∴20r=60,解得r=3,∴内切圆的直径为6步,
即能容纳的最大圆的直径为6步.
5.4
解析 如图,
∵四边形CDEF为正方形,∴∠D=90°,CD=DE,
∴CE为直径,∠ECD=45°,
由题意得AB=2.5尺,
∴CE=2.5-0.25×2=2尺,
∴CD=CE·cos∠ECD=2× 尺,
∴正方形CDEF的周长为4 尺.故答案为4.
6.A ∵sec A=,sec B=,sin A=,cos B=,
∴sec B·sin A==1,sec A·cos B=,sec2A·sec2B=,故选A.
7.
解析 sin 15°=sin(45°-30°)=sin 45°cos 30°-cos 45°sin 30°=.
8.(3,0)或(4,0)
解析 当k=0时,函数解析式为y=-x-3,此时,函数图象与x轴只有一个交点,它的“Y函数”解析式为y=x-3,∴y=-x-3的“Y函数”图象与x轴的交点坐标为(3,0);
当k≠0时,此函数为二次函数,若二次函数y=x2+(k-1)x+k-3的图象与x轴只有一个交点,则b2-4ac=(k-1)2-4××(k-3)=k+1=0,解得k=-1,∴二次函数的解析式为y=-x2-2x-4,即y=-(x+4)2,∴它的“Y函数”解析式为y=-(x-4)2,令y=0,则-(x-4)2=0,∴x1=x2=4,∴二次函数y=-(x+4)2的“Y函数”图象与x轴的交点坐标为(4,0).
综上,它的“Y函数”图象与x轴的交点坐标为(3,0)或(4,0).
9.①②③④
解析 ①∵(-1,0),(3,0)和(0,3)都满足函数y=|x2-2x-3|,∴①是正确的;
②从图象可知图象具有对称性,对称轴可用对称轴公式求得,是直线x=1,∴②是正确的;③根据函数的图象,发现当-1≤x≤1或x≥3时,函数值y随x值的增大而增大,∴③是正确的;④函数图象的最低点就是图象与x轴的两个交点,当x=-1或x=3时,y=0,∴④是正确的;⑤从图象上看,图象无最高点,故函数无最大值,∴⑤不正确.故答案是①②③④.
10.解析 (1).
详解:∵a=2,∴,∴焦点坐标为,准线方程为y=-.
(2)∵a==-2,∴准线方程为y=-2,
∴点P的纵坐标为4,∴,
∴点P的坐标为(4,4)或(-4,4).
(3)如图,作AG⊥l于G,作BK⊥l于K,
∴AG=AF=4,BK=BF,FH=,
∵BK∥FH∥AG,
∴△CBK∽△CFH,△CBK∽△CAG,
∴,
∴,解得a=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024北师大版数学九年级下学期
专项素养综合全练(九)
数学文化与新定义型试题
类型一 数学文化
1.西周时期,丞相周公旦设置过一种通过测定日影长度来确定时间的仪器,称为圭表,下图是一个根据长春的地理位置设计的圭表,其中,立柱AC的高为a,已知冬至时长春的正午日光入射角∠ABC约为23°,则立柱根部与圭表的冬至线的距离(即BC的长)约为( )
A. B.asin 23° C. D.atan 23°
2.(2023山东东营中考)“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问:径几何 ”转化为现在的数学语言表达就是:如图,CD为☉O的直径,弦AB⊥CD,垂足为E,CE=1寸,AB=10寸,则直径CD的长度为
寸.
3.(2022湖南株洲中考)中国元代数学家朱世杰所著《四元玉鉴》记载有“锁套吞容”之“方田圆池结角池图”.“方田一段,一角圆池占之.”意思是:一块正方形田地,在其一角有一个圆形的水池(其中圆与正方形一角的两边均相切),如图所示.问题:此图中,正方形一条对角线AB与☉O相交于点M、N(点N在点M的右上方),若AB的长度为10丈,☉O的半径为2丈,则BN的长度为 丈.
4.(2022北京门头沟期末)《九章算术》是我国古代的数学名著,书中有这样的一个问题:“今有勾八步,股十五步,问勾中容圆径几何 ”其意思是:如图,现有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问:该直角三角形所能容纳的最大圆的直径是多少
答:该直角三角形所能容纳的最大圆的直径是 步.
5.(2020湖南株洲中考)据《汉书·律历志》记载:“量者,龠(yuè)、合、升、斗、斛(hú)也.”斛是中国古代的一种量器.“斛底,方而圜(huán)其外,旁有庣(tiāo)焉.”意思是:斛的底面为正方形外接一个圆,此圆外是一个同心圆,如图所示.问题:现有一斛,其底面的外圆直径为两尺五寸(即2.5尺),“庣旁”为两寸五分(即两同心圆的外圆与内圆的半径之差为0.25尺),则此斛底面的正方形的周长为 尺.(结果用最简根式表示)
类型二 新定义型试题
6.如图,在△ABC中,∠C=90°,定义:斜边与∠A的邻边的比叫做∠A的正割,用“sec A”表示,若设该直角三角形的各边分别为a,b,c,则sec A=,下列选项正确的是( )
A.sec B·sin A=1 B.sec B= C.sec A·cos B=1 D.sec2A·sec2B=1
7.(2022黑龙江绥化中考)定义一种运算:
sin(α+β)=sin αcos β+cos αsin β,sin(α-β)=sin αcos β-cos αsin β.
例如:当α=45°,β=30°时,sin(45°+30°)=,则
sin 15°的值为 .
8.(2023四川巴中中考)规定:如果两个函数的图象关于y轴对称,那么称这两个函数互为“Y函数”.例如:函数y=x+3与y=-x+3互为“Y函数”.若函数y=x2+(k-1)x+k-3的图象与x轴只有一个交点,则它的“Y函数”图象与x轴的交点坐标为 .
9.(2023四川自贡沿滩月考)我们定义一种新函数:形如y=|ax2+bx+c|(a
≠0,b2-4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=
|x2-2x-3|的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为(-1,0),(3,0)和(0,3);②图象具有对称性,对称轴是直线x=1;③当-1≤
x≤1或x≥3时,函数值y随x值的增大而增大;④当x=-1或x=3时,函数有最小值,是0;⑤当x=1时,函数有最大值,是4.其中正确的结论有
.(填正确的序号)
10.(2022湖北鄂州中考节选)某数学兴趣小组运用《几何画板》软件探究y=ax2(a>0)的图象.发现:如图1所示,该类型图象上任意一点M到定点F的距离MF,始终等于它到定直线l:y=-的距离MN
(该结论不需要证明),他们称:定点F为图象的焦点,定直线l为图象的准线,y=-叫做抛物线的准线方程.其中原点O为FH的中点,FH=
2OF=.例如:抛物线y=x2,其焦点坐标为F,准线方程为l:y=-.其中MF=MN,FH=2OF=1.
【基础训练】(1)请分别直接写出抛物线y=2x2的焦点坐标和准线l的方程: , .
【技能训练】(2)如图2所示,已知抛物线y=x2上一点P到准线l的距离为6,求点P的坐标.
【能力提升】(3)如图3所示,已知过抛物线y=ax2(a>0)的焦点F的直线依次交抛物线及准线l于点A、B、C.若BC=2BF,AF=4,求a的值.
图1 图2 图3
答案全解全析
1.C 由题意可得,立柱根部与圭表的冬至线的距离为,故选C.
2.26
解析 连接OA,设☉O的半径是r寸,
∵直径CD⊥AB,∴AE=×10=5寸,
∵CE=1寸,∴OE=(r-1)寸,
∵OA2=OE2+AE2,∴r2=(r-1)2+52,∴r=13,
∴直径CD的长度为2×13=26寸.故答案为26.
3.(8-2)
解析 根据题意易知圆心O在AB上,如图,设正方形的一边与☉O的切点为C,连接OC,则OC⊥AC,
∵四边形是正方形,AB是对角线,∴∠OAC=45°,
∴OA=(丈),
∴BN=AB-AN=10-(2)丈,
故答案为(8-2).
4.6
解析 如图:
在Rt△ABC中,AC=8步,BC=15步,∠ACB=90°,
∴AB==17步,
S△ABC=AC·BC=×8×15=60(步2),
设内切圆的圆心为O,分别连接圆心和三个切点,及OA、OB、OC,
设内切圆的半径为r步,
∴S△ABC=S△AOB+S△BOC+S△AOC=r·(AB+BC+AC)=20r(步2),
∴20r=60,解得r=3,∴内切圆的直径为6步,
即能容纳的最大圆的直径为6步.
5.4
解析 如图,
∵四边形CDEF为正方形,∴∠D=90°,CD=DE,
∴CE为直径,∠ECD=45°,
由题意得AB=2.5尺,
∴CE=2.5-0.25×2=2尺,
∴CD=CE·cos∠ECD=2× 尺,
∴正方形CDEF的周长为4 尺.故答案为4.
6.A ∵sec A=,sec B=,sin A=,cos B=,
∴sec B·sin A==1,sec A·cos B=,sec2A·sec2B=,故选A.
7.
解析 sin 15°=sin(45°-30°)=sin 45°cos 30°-cos 45°sin 30°=.
8.(3,0)或(4,0)
解析 当k=0时,函数解析式为y=-x-3,此时,函数图象与x轴只有一个交点,它的“Y函数”解析式为y=x-3,∴y=-x-3的“Y函数”图象与x轴的交点坐标为(3,0);
当k≠0时,此函数为二次函数,若二次函数y=x2+(k-1)x+k-3的图象与x轴只有一个交点,则b2-4ac=(k-1)2-4××(k-3)=k+1=0,解得k=-1,∴二次函数的解析式为y=-x2-2x-4,即y=-(x+4)2,∴它的“Y函数”解析式为y=-(x-4)2,令y=0,则-(x-4)2=0,∴x1=x2=4,∴二次函数y=-(x+4)2的“Y函数”图象与x轴的交点坐标为(4,0).
综上,它的“Y函数”图象与x轴的交点坐标为(3,0)或(4,0).
9.①②③④
解析 ①∵(-1,0),(3,0)和(0,3)都满足函数y=|x2-2x-3|,∴①是正确的;
②从图象可知图象具有对称性,对称轴可用对称轴公式求得,是直线x=1,∴②是正确的;③根据函数的图象,发现当-1≤x≤1或x≥3时,函数值y随x值的增大而增大,∴③是正确的;④函数图象的最低点就是图象与x轴的两个交点,当x=-1或x=3时,y=0,∴④是正确的;⑤从图象上看,图象无最高点,故函数无最大值,∴⑤不正确.故答案是①②③④.
10.解析 (1).
详解:∵a=2,∴,∴焦点坐标为,准线方程为y=-.
(2)∵a==-2,∴准线方程为y=-2,
∴点P的纵坐标为4,∴,
∴点P的坐标为(4,4)或(-4,4).
(3)如图,作AG⊥l于G,作BK⊥l于K,
∴AG=AF=4,BK=BF,FH=,
∵BK∥FH∥AG,
∴△CBK∽△CFH,△CBK∽△CAG,
∴,
∴,解得a=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
