第二章 二次函数期末章节提升练习(含答案)
文档属性
| 名称 | 第二章 二次函数期末章节提升练习(含答案) | 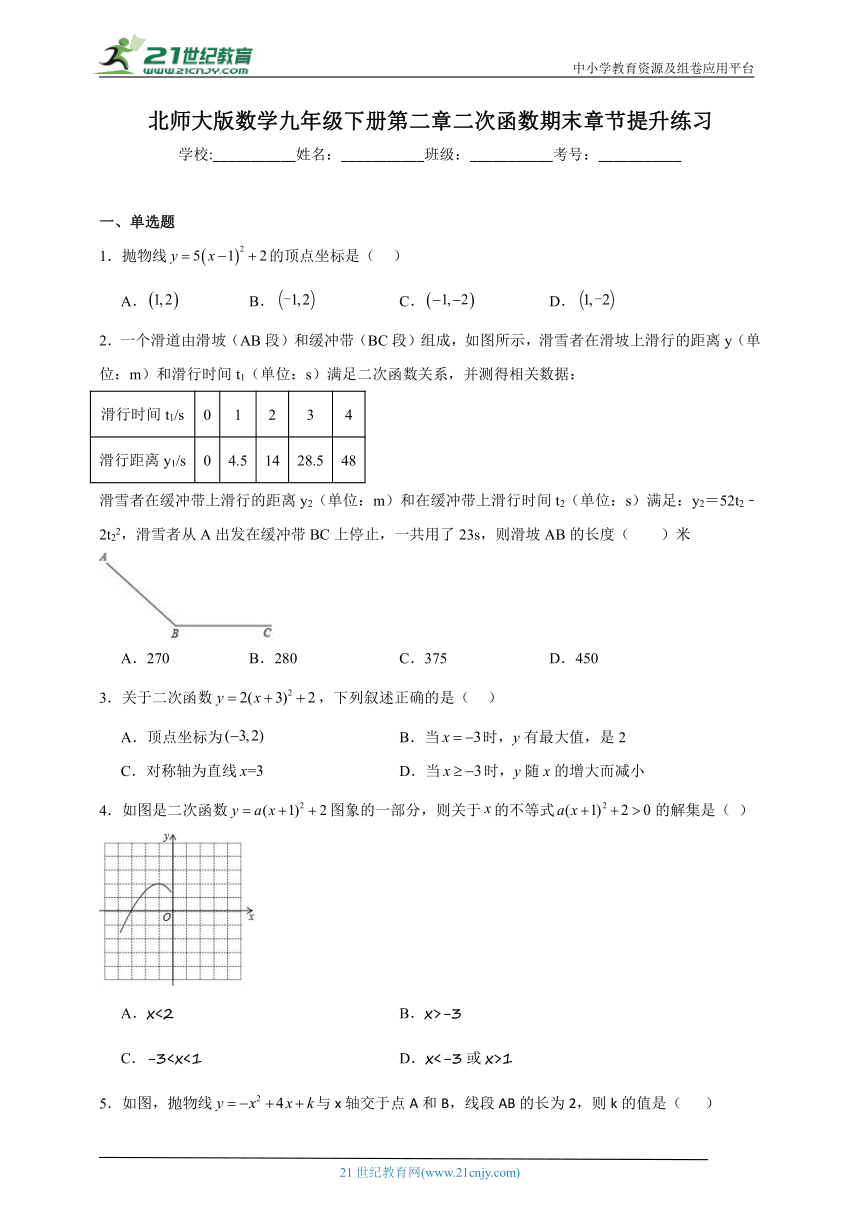 | |
| 格式 | docx | ||
| 文件大小 | 618.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-27 04:46:11 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
北师大版数学九年级下册第二章二次函数期末章节提升练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.抛物线的顶点坐标是( )
A. B. C. D.
2.一个滑道由滑坡(AB段)和缓冲带(BC段)组成,如图所示,滑雪者在滑坡上滑行的距离y(单位:m)和滑行时间t1(单位:s)满足二次函数关系,并测得相关数据:
滑行时间t1/s 0 1 2 3 4
滑行距离y1/s 0 4.5 14 28.5 48
滑雪者在缓冲带上滑行的距离y2(单位:m)和在缓冲带上滑行时间t2(单位:s)满足:y2=52t2﹣2t22,滑雪者从A出发在缓冲带BC上停止,一共用了23s,则滑坡AB的长度( )米
A.270 B.280 C.375 D.450
3.关于二次函数,下列叙述正确的是( )
A.顶点坐标为 B.当时,y有最大值,是2
C.对称轴为直线 D.当时,y随x的增大而减小
4.如图是二次函数图象的一部分,则关于的不等式的解集是( )
A.x<2 B.x>-3
C.-31
5.如图,抛物线与x轴交于点A和B,线段AB的长为2,则k的值是( )
A.3 B. 3 C. 4 D. 5
6.若二次函数的图象与x轴有两个交点A 和B,顶点为C,且满足, 则=( )
A.30° B.135° C.60° D.90°
7.已知,点,,都在函数的图象上,则( )
A. B. C. D.
8.已知点P(m,n)在抛物线上,当m≤1时,总有成立,则a的取值范围( )
A.a≥1 B.09.下列命题是真命题的有 ( )
①方程的解是;
②连接矩形各边中点的四边形是菱形;
③如果将抛物线向右平移1个单位,那么所得新抛物线的表达式为;
④若反比例函数的图象上有两点、,则.
A. 个 B. 个 C. 个 D. 个
10.若抛物线与抛物线关于直线对称,则m,n的值为( )
A., B., C., D.,
二、填空题
11.老师让写出一个二次函数,满足以下3个性质.
1:函数图象的顶点在轴上;2:当时,随的增大而减小;
3:该函数的形状与函数的图象相同
甲同学写出几个二次函数表达式:
①②③④
请问甲同学写出的二次函数表达式哪些符合上述3个性质 .
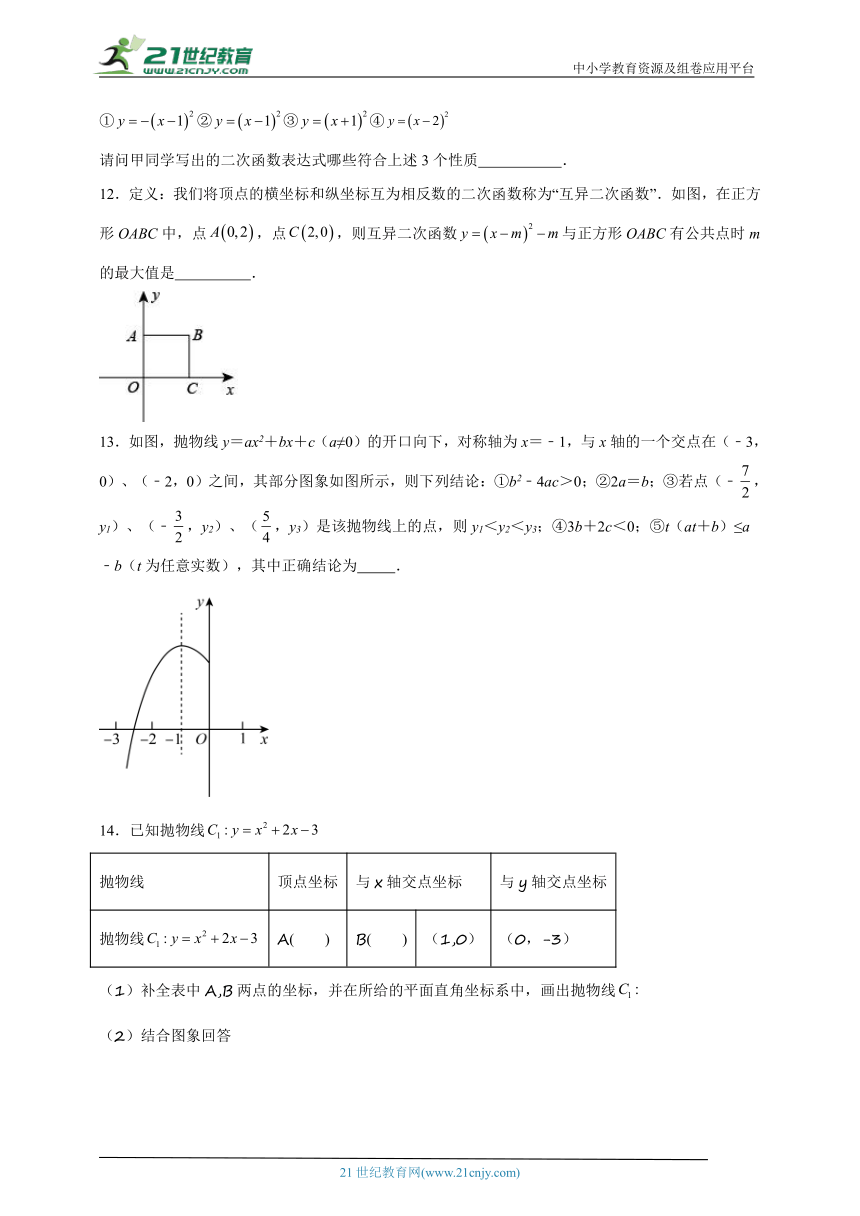
12.定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形OABC中,点,点,则互异二次函数与正方形OABC有公共点时m的最大值是 .
13.如图,抛物线y=ax2+bx+c(a≠0)的开口向下,对称轴为x=﹣1,与x轴的一个交点在(﹣3,0)、(﹣2,0)之间,其部分图象如图所示,则下列结论:①b2﹣4ac>0;②2a=b;③若点(﹣,y1)、(﹣,y2)、(,y3)是该抛物线上的点,则y1<y2<y3;④3b+2c<0;⑤t(at+b)≤a﹣b(t为任意实数),其中正确结论为 .
14.已知抛物线
抛物线 顶点坐标 与x轴交点坐标 与y轴交点坐标
抛物线 A( ) B( ) (1,0) (0,-3)
(1)补全表中A,B两点的坐标,并在所给的平面直角坐标系中,画出抛物线
(2)结合图象回答
①当x的取值范围为 时,y随x的增大而增大;
②当x 时,;
③当时,y的取值范围 .
15.当时,关于的二次函数的图象在轴上方,则的取值范围为 .
16.已知关于的一元二次方程的一个根为,且抛物线的对称轴是直线,则抛物线的顶点坐标为 .
17.将二次函数的图象向下平移3个单位长度,再向右平移3个单位长度,得到的抛物线的解析式为 .
18.若抛物线与x轴有公共点,则m的取值范围为 .
19.已知函数是关于的二次函数,则的值为 .
20.抛物线y=2(x-4)2+1的顶点坐标为 .
三、解答题
21.已知一个二次函数的图象经过A(0,﹣3),B(1,0),C(m,2m+3),D(﹣1,﹣2)四点,求这个函数解析式以及点C的坐标.
22.如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
23.如图,在四边形ABCD中,ABCD,∠D=90°,AC⊥BC,DC=8cm,AD=6cm.点F从A点出发,以2cm/s的速度沿AB向点B匀速运动,同时,点E从B点出发,以1 cm/s的速度沿BC向点C匀速运动.当其中一点到达终点时,两点都停止运动,设运动时间为t(s).
(1)求AB长度;
(2)设四边形ACEF的面积为y (cm2),求y与t的函数关系式;
(3)是否存在某一时刻t,使得四边形ACEF的面积是△ACD的面积的倍?若存在,求出此时t的值;若不存在,说明理由.
(4)求t为何值时△BEF为直角三角形.
24.如图,在平面直角坐标系中,的边在x轴上,,以A为顶点的抛物线经过点,交y轴于点,动点P在对称轴上.
(1)求抛物线的解析式.
(2)若点P从A点出发,沿方向以1个单位长度/秒的速度匀速运动到点B停止,设运动时间为t秒,过点P作交于点D,过点D且平行于y轴的直线l交抛物线于点Q,连接,当t为何值时,的面积最大?最大值是多少?
(3)抛物线上是否存在点M,使得以点P,M,E,C为顶点的四边形是平行四边形?若存在,请求出点M的坐标;若不存在,请说明理由.
25.已知:如图1,在矩形ABCD中,AC是对角线,.点P从点A出发,沿AB方向匀速运动,速度为;同时,点Q从点C出发,沿CA方向匀速运动,速度为.过点Q作,QE与BC相交于点E,连接PQ,设运动时间为,解答下列问题:
(1)连接BQ,当t为何值时,点E在线段BQ的垂直平分线上?
(2)设四边形BPQC的面积为,求y与t之间的函数关系式;并求四边形BPQC的面积为y是矩形ABCD面积的十二分之五时的t的值,
(3)如图2,取点E关于AC的对称点F,是否存在某一时刻t,使为等腰三角形?若存在,直接写出t的值(不需提供解答过程);若不存在,请说明理由.
(4)t为何值时,Q、F、D三点共线?
参考答案:
1.A
2.A
3.A
4.C
5.B
6.D
7.D
8.D
9.B
10.C
11.②④/④②
12.
13.①②④⑤
14.(1)略 (2) ①x>-1 ②x<-3或x>1 ③-4≤y<0
15.或
16.(2,3)
17.
18.
19.
20.(4,1)
21.y=2x2+x﹣3,C点坐标为(﹣,0)或(2,7)
22.(1)y=﹣(x+1)2+4,顶点坐标为(﹣1,4);(2)①点P(﹣﹣1,2);②P(﹣ ,)
23.(1);(2);(3)存在,或;(4)或
24.(1)
(2)当时,的面积最大,最大值为1;
(3)存在点M,使得以点P,M,E,C为顶点的四边形是平行四边形,点M的坐标为或.
25.(1)t=2
(2);或
(3)或
(4)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
北师大版数学九年级下册第二章二次函数期末章节提升练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.抛物线的顶点坐标是( )
A. B. C. D.
2.一个滑道由滑坡(AB段)和缓冲带(BC段)组成,如图所示,滑雪者在滑坡上滑行的距离y(单位:m)和滑行时间t1(单位:s)满足二次函数关系,并测得相关数据:
滑行时间t1/s 0 1 2 3 4
滑行距离y1/s 0 4.5 14 28.5 48
滑雪者在缓冲带上滑行的距离y2(单位:m)和在缓冲带上滑行时间t2(单位:s)满足:y2=52t2﹣2t22,滑雪者从A出发在缓冲带BC上停止,一共用了23s,则滑坡AB的长度( )米
A.270 B.280 C.375 D.450
3.关于二次函数,下列叙述正确的是( )
A.顶点坐标为 B.当时,y有最大值,是2
C.对称轴为直线 D.当时,y随x的增大而减小
4.如图是二次函数图象的一部分,则关于的不等式的解集是( )
A.x<2 B.x>-3
C.-3
5.如图,抛物线与x轴交于点A和B,线段AB的长为2,则k的值是( )
A.3 B. 3 C. 4 D. 5
6.若二次函数的图象与x轴有两个交点A 和B,顶点为C,且满足, 则=( )
A.30° B.135° C.60° D.90°
7.已知,点,,都在函数的图象上,则( )
A. B. C. D.
8.已知点P(m,n)在抛物线上,当m≤1时,总有成立,则a的取值范围( )
A.a≥1 B.0
①方程的解是;
②连接矩形各边中点的四边形是菱形;
③如果将抛物线向右平移1个单位,那么所得新抛物线的表达式为;
④若反比例函数的图象上有两点、,则.
A. 个 B. 个 C. 个 D. 个
10.若抛物线与抛物线关于直线对称,则m,n的值为( )
A., B., C., D.,
二、填空题
11.老师让写出一个二次函数,满足以下3个性质.
1:函数图象的顶点在轴上;2:当时,随的增大而减小;
3:该函数的形状与函数的图象相同
甲同学写出几个二次函数表达式:
①②③④
请问甲同学写出的二次函数表达式哪些符合上述3个性质 .
12.定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形OABC中,点,点,则互异二次函数与正方形OABC有公共点时m的最大值是 .
13.如图,抛物线y=ax2+bx+c(a≠0)的开口向下,对称轴为x=﹣1,与x轴的一个交点在(﹣3,0)、(﹣2,0)之间,其部分图象如图所示,则下列结论:①b2﹣4ac>0;②2a=b;③若点(﹣,y1)、(﹣,y2)、(,y3)是该抛物线上的点,则y1<y2<y3;④3b+2c<0;⑤t(at+b)≤a﹣b(t为任意实数),其中正确结论为 .
14.已知抛物线
抛物线 顶点坐标 与x轴交点坐标 与y轴交点坐标
抛物线 A( ) B( ) (1,0) (0,-3)
(1)补全表中A,B两点的坐标,并在所给的平面直角坐标系中,画出抛物线
(2)结合图象回答
①当x的取值范围为 时,y随x的增大而增大;
②当x 时,;
③当时,y的取值范围 .
15.当时,关于的二次函数的图象在轴上方,则的取值范围为 .
16.已知关于的一元二次方程的一个根为,且抛物线的对称轴是直线,则抛物线的顶点坐标为 .
17.将二次函数的图象向下平移3个单位长度,再向右平移3个单位长度,得到的抛物线的解析式为 .
18.若抛物线与x轴有公共点,则m的取值范围为 .
19.已知函数是关于的二次函数,则的值为 .
20.抛物线y=2(x-4)2+1的顶点坐标为 .
三、解答题
21.已知一个二次函数的图象经过A(0,﹣3),B(1,0),C(m,2m+3),D(﹣1,﹣2)四点,求这个函数解析式以及点C的坐标.
22.如图,抛物线y=ax2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,3),其对称轴l为x=﹣1.
(1)求抛物线的解析式并写出其顶点坐标;
(2)若动点P在第二象限内的抛物线上,动点N在对称轴l上.
①当PA⊥NA,且PA=NA时,求此时点P的坐标;
②当四边形PABC的面积最大时,求四边形PABC面积的最大值及此时点P的坐标.
23.如图,在四边形ABCD中,ABCD,∠D=90°,AC⊥BC,DC=8cm,AD=6cm.点F从A点出发,以2cm/s的速度沿AB向点B匀速运动,同时,点E从B点出发,以1 cm/s的速度沿BC向点C匀速运动.当其中一点到达终点时,两点都停止运动,设运动时间为t(s).
(1)求AB长度;
(2)设四边形ACEF的面积为y (cm2),求y与t的函数关系式;
(3)是否存在某一时刻t,使得四边形ACEF的面积是△ACD的面积的倍?若存在,求出此时t的值;若不存在,说明理由.
(4)求t为何值时△BEF为直角三角形.
24.如图,在平面直角坐标系中,的边在x轴上,,以A为顶点的抛物线经过点,交y轴于点,动点P在对称轴上.
(1)求抛物线的解析式.
(2)若点P从A点出发,沿方向以1个单位长度/秒的速度匀速运动到点B停止,设运动时间为t秒,过点P作交于点D,过点D且平行于y轴的直线l交抛物线于点Q,连接,当t为何值时,的面积最大?最大值是多少?
(3)抛物线上是否存在点M,使得以点P,M,E,C为顶点的四边形是平行四边形?若存在,请求出点M的坐标;若不存在,请说明理由.
25.已知:如图1,在矩形ABCD中,AC是对角线,.点P从点A出发,沿AB方向匀速运动,速度为;同时,点Q从点C出发,沿CA方向匀速运动,速度为.过点Q作,QE与BC相交于点E,连接PQ,设运动时间为,解答下列问题:
(1)连接BQ,当t为何值时,点E在线段BQ的垂直平分线上?
(2)设四边形BPQC的面积为,求y与t之间的函数关系式;并求四边形BPQC的面积为y是矩形ABCD面积的十二分之五时的t的值,
(3)如图2,取点E关于AC的对称点F,是否存在某一时刻t,使为等腰三角形?若存在,直接写出t的值(不需提供解答过程);若不存在,请说明理由.
(4)t为何值时,Q、F、D三点共线?
参考答案:
1.A
2.A
3.A
4.C
5.B
6.D
7.D
8.D
9.B
10.C
11.②④/④②
12.
13.①②④⑤
14.(1)略 (2) ①x>-1 ②x<-3或x>1 ③-4≤y<0
15.或
16.(2,3)
17.
18.
19.
20.(4,1)
21.y=2x2+x﹣3,C点坐标为(﹣,0)或(2,7)
22.(1)y=﹣(x+1)2+4,顶点坐标为(﹣1,4);(2)①点P(﹣﹣1,2);②P(﹣ ,)
23.(1);(2);(3)存在,或;(4)或
24.(1)
(2)当时,的面积最大,最大值为1;
(3)存在点M,使得以点P,M,E,C为顶点的四边形是平行四边形,点M的坐标为或.
25.(1)t=2
(2);或
(3)或
(4)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
