高中说课课件
图片预览








文档简介
课件24张PPT。遵义市第二中学 郑维俊等差数列的前n项和
(第一课时) 第一部分 教材分析
第二部分 教法分析
第三部分 学法分析
第四部分 教学过程设计1、教材的地位和作用
本节课要研究的“等差数列的前n项和”是在学习了“数列”和“等差数列”的基础上进行学习的,它既是前面所学知识的延续和深化,又是后面学习“等比数列及其前n项和”的基础和前奏。因此,学好了本节课的内容,既能加深对数列有关概念的理解,又能为后面学好等比数列及数列求和提供方法。等差数列求和有着广泛的实际应用,如计算堆放物品的总数、剧场座位总数的计算、分期存款一次取出的储蓄利息的计算等问题。所以我们有必要进一步研究等差数列。本节课的学习还蕴涵着深刻的数学思想方法(特殊到一般的思想、转化思想、方程思想、数形结合思想),教学中有针对性地对学生进行这方面渗透,有利于学生数学思维能力的提高。
第一部分 教材分析
根据教学大纲的要求,我把本节课的教学目标确定为:
⑴ 知识目标:让学生掌握等差数列前n项和公式,并
能运用公式解决一些简单的问题。
⑵ 能力目标:通过教学培养学生观察、比较、归纳
能力和分析问题、解决问题的能力。
⑶ 情感目标:激发学生探究数学问题的兴趣,优化
学生的思维品质。2、教学目标 ⑴ 重点:等差数列前n项和公式
⑵ 难点:获得推导公式的思路
⑶ 关键:通过具体例子发现一般规律
3、教学重点、难点及关键
由于本节课是学生学习数列的深化阶段,是学生认识和掌握数列的关键期,因此要了解学生的已有基础和亲身体验,主要采用“引导发现法”让学生在学习等差数列的前n项和的同时经历一个“实验、探索、推导”的科学教学过程,体现从特殊到一般的认识规律,通过学生“动手、动脑、讨论、演练”增加学生的参与机会,增强参与意识,教给学生获取知识的途径,思考问题的方法,使学生真正成为教学主体。第二部分 教法分析 建构主义学习理论认为,学习是学生积极主动的建构知识的过程,学习应该与学生熟悉的背景相联系。在教学中,让学生在问题情境中,经历知识的形成和发展,通过观察、操作、归纳、思考、探索、主动交流、反思参与学习,认识和理解数学知识,学会学习,发展能力。 第三部分 学法分析创设情境,引入新课
演示启发,探索求知
特殊到一般,推导公式
巩固练习,举例应用
小结深化,整体把握 第四部分 教学过程设计问题情境1:
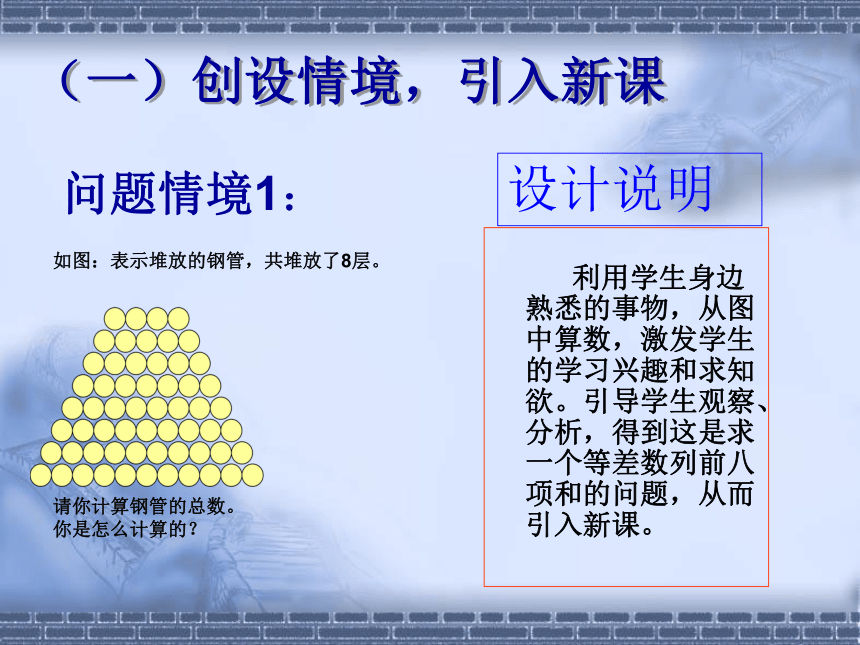
如图:表示堆放的钢管,共堆放了8层。
请你计算钢管的总数。
你是怎么计算的?
利用学生身边熟悉的事物,从图中算数,激发学生的学习兴趣和求知欲。引导学生观察、分析,得到这是求一个等差数列前八项和的问题,从而引入新课。
设计说明(一)创设情境,引入新课 借助几何图形的直观性,引导学生使用熟悉的几何方法:把“全等梯形”倒置,与原图补成平行四边形。计算钢管总数设计说明 几何直观能启迪思路,帮助理解,因此,借助几何直观学习和理解数学,是数学学习中的重要方面。只有做到了直观上的理解,才是真正的理解。因此在教学中,要鼓励学生借助几何直观进行思考,揭示研究对象的性质和关系,从而渗透了数形结合的数学思想。 问题与情景2求1到100的正整数之和。
意在让学生体验“倒序相加求和”这一算法的合理性,从心理上完成对“首尾配对求和”算法的改进。为求一般等差数列前n项和作铺垫.(二)讲授新课令等差数列{ }的前 项和为 ,公差为的 ,则
①
②
①+②得,
∴
问题与情境3:如何求等差数列 的前 项和?等差数列 的前 n 项和公式说 明: ① 等差数列的前n项和等于首末项的和与项数乘积的一半,与梯形面积
公式(上底+下底)×高÷2相类比;
② 这种求和方法称作倒序相加法;
③ 将 代入 (Ⅰ),
得 (Ⅱ)
④ 在等差数列的通项公式及前n项和公式中,共有五个元素,即 、 、 、 、 ,一般说来,只要知道了其中三个元素,通过解方程
或方程组就可以求出其余两个元素。(简称“知三求二”)
公式应用选用公式
变用公式
知三求二(三)例题讲解及练习公式应用 本例提供了许多数据信息,学生可以从首项、尾项、项数出发,使用公式1,也可以从首项、公差、项数出发,使用公式2求和。达到学生熟悉公式的要素与结构的教学目的。
通过两种方法的比较,引导学生应该根据信息选择适当的公式,以便于计算。 选用公式公式应用变用公式 例2 等差数列-10,-6,-2,2,…的前多少项的和为54? 本例已知首项,前n项和、并且可以求出公差,利用公式2求项数。
事实上,在两个求和公式中各包含四个元素,从方程的角度,知三必能求余一。 变式练习公式应用公式应用知三求二 本例是使用等差数列的求和公式和通项公式求未知元。
可以使用公式2,先求出首项,再使用通项公式求尾项。也可以使用公式1和通项公式,联列方程组求解。
事实上,在求和公式、通项公式中共有首项、公差、项数、尾项、前n项和五个元素,如果已知其中三个,联列方程组,就可求其余二个。“基本量法”(四)课 堂 小 结
⑴ 等差数列前 项和的推导方法(倒序相加法)。
⑵ 等差数列前 项和的两个公式分别是什么?
⑶ 解题中体现了哪些数学思想、方法?
⑷ 如何理解“知三求二”?设计说明:以设问的形式进行小结,让学生主动参与,发现问题,自查自纠,相互补充,达到掌握基础和重点的目的。(五)布置作业A必做题:课本118页,练习1、2、3;习题3.3 第2题(3、4)
B选做题:在等差数列中,
必做题是让学生巩固所学的知识,熟练公式的应用。根据我校的特点,为了促进数学成绩优秀学生的发展,培养他们分析问题解决问题的能力,我设计了选做题,达到分层教学的目的。 (六)课后反思 1、通过层层递进思维过程来寻求推导等差数列前项和的思路-----“倒序相加法”突破了本节课的难点。
2、通过例题和练习突出了本节课的重点。
3、本节课学生还不能灵活地选用公式,要加强练习。 (七)板书设计设计说明谢谢 再见
(第一课时) 第一部分 教材分析
第二部分 教法分析
第三部分 学法分析
第四部分 教学过程设计1、教材的地位和作用
本节课要研究的“等差数列的前n项和”是在学习了“数列”和“等差数列”的基础上进行学习的,它既是前面所学知识的延续和深化,又是后面学习“等比数列及其前n项和”的基础和前奏。因此,学好了本节课的内容,既能加深对数列有关概念的理解,又能为后面学好等比数列及数列求和提供方法。等差数列求和有着广泛的实际应用,如计算堆放物品的总数、剧场座位总数的计算、分期存款一次取出的储蓄利息的计算等问题。所以我们有必要进一步研究等差数列。本节课的学习还蕴涵着深刻的数学思想方法(特殊到一般的思想、转化思想、方程思想、数形结合思想),教学中有针对性地对学生进行这方面渗透,有利于学生数学思维能力的提高。
第一部分 教材分析
根据教学大纲的要求,我把本节课的教学目标确定为:
⑴ 知识目标:让学生掌握等差数列前n项和公式,并
能运用公式解决一些简单的问题。
⑵ 能力目标:通过教学培养学生观察、比较、归纳
能力和分析问题、解决问题的能力。
⑶ 情感目标:激发学生探究数学问题的兴趣,优化
学生的思维品质。2、教学目标 ⑴ 重点:等差数列前n项和公式
⑵ 难点:获得推导公式的思路
⑶ 关键:通过具体例子发现一般规律
3、教学重点、难点及关键
由于本节课是学生学习数列的深化阶段,是学生认识和掌握数列的关键期,因此要了解学生的已有基础和亲身体验,主要采用“引导发现法”让学生在学习等差数列的前n项和的同时经历一个“实验、探索、推导”的科学教学过程,体现从特殊到一般的认识规律,通过学生“动手、动脑、讨论、演练”增加学生的参与机会,增强参与意识,教给学生获取知识的途径,思考问题的方法,使学生真正成为教学主体。第二部分 教法分析 建构主义学习理论认为,学习是学生积极主动的建构知识的过程,学习应该与学生熟悉的背景相联系。在教学中,让学生在问题情境中,经历知识的形成和发展,通过观察、操作、归纳、思考、探索、主动交流、反思参与学习,认识和理解数学知识,学会学习,发展能力。 第三部分 学法分析创设情境,引入新课
演示启发,探索求知
特殊到一般,推导公式
巩固练习,举例应用
小结深化,整体把握 第四部分 教学过程设计问题情境1:
如图:表示堆放的钢管,共堆放了8层。
请你计算钢管的总数。
你是怎么计算的?
利用学生身边熟悉的事物,从图中算数,激发学生的学习兴趣和求知欲。引导学生观察、分析,得到这是求一个等差数列前八项和的问题,从而引入新课。
设计说明(一)创设情境,引入新课 借助几何图形的直观性,引导学生使用熟悉的几何方法:把“全等梯形”倒置,与原图补成平行四边形。计算钢管总数设计说明 几何直观能启迪思路,帮助理解,因此,借助几何直观学习和理解数学,是数学学习中的重要方面。只有做到了直观上的理解,才是真正的理解。因此在教学中,要鼓励学生借助几何直观进行思考,揭示研究对象的性质和关系,从而渗透了数形结合的数学思想。 问题与情景2求1到100的正整数之和。
意在让学生体验“倒序相加求和”这一算法的合理性,从心理上完成对“首尾配对求和”算法的改进。为求一般等差数列前n项和作铺垫.(二)讲授新课令等差数列{ }的前 项和为 ,公差为的 ,则
①
②
①+②得,
∴
问题与情境3:如何求等差数列 的前 项和?等差数列 的前 n 项和公式说 明: ① 等差数列的前n项和等于首末项的和与项数乘积的一半,与梯形面积
公式(上底+下底)×高÷2相类比;
② 这种求和方法称作倒序相加法;
③ 将 代入 (Ⅰ),
得 (Ⅱ)
④ 在等差数列的通项公式及前n项和公式中,共有五个元素,即 、 、 、 、 ,一般说来,只要知道了其中三个元素,通过解方程
或方程组就可以求出其余两个元素。(简称“知三求二”)
公式应用选用公式
变用公式
知三求二(三)例题讲解及练习公式应用 本例提供了许多数据信息,学生可以从首项、尾项、项数出发,使用公式1,也可以从首项、公差、项数出发,使用公式2求和。达到学生熟悉公式的要素与结构的教学目的。
通过两种方法的比较,引导学生应该根据信息选择适当的公式,以便于计算。 选用公式公式应用变用公式 例2 等差数列-10,-6,-2,2,…的前多少项的和为54? 本例已知首项,前n项和、并且可以求出公差,利用公式2求项数。
事实上,在两个求和公式中各包含四个元素,从方程的角度,知三必能求余一。 变式练习公式应用公式应用知三求二 本例是使用等差数列的求和公式和通项公式求未知元。
可以使用公式2,先求出首项,再使用通项公式求尾项。也可以使用公式1和通项公式,联列方程组求解。
事实上,在求和公式、通项公式中共有首项、公差、项数、尾项、前n项和五个元素,如果已知其中三个,联列方程组,就可求其余二个。“基本量法”(四)课 堂 小 结
⑴ 等差数列前 项和的推导方法(倒序相加法)。
⑵ 等差数列前 项和的两个公式分别是什么?
⑶ 解题中体现了哪些数学思想、方法?
⑷ 如何理解“知三求二”?设计说明:以设问的形式进行小结,让学生主动参与,发现问题,自查自纠,相互补充,达到掌握基础和重点的目的。(五)布置作业A必做题:课本118页,练习1、2、3;习题3.3 第2题(3、4)
B选做题:在等差数列中,
必做题是让学生巩固所学的知识,熟练公式的应用。根据我校的特点,为了促进数学成绩优秀学生的发展,培养他们分析问题解决问题的能力,我设计了选做题,达到分层教学的目的。 (六)课后反思 1、通过层层递进思维过程来寻求推导等差数列前项和的思路-----“倒序相加法”突破了本节课的难点。
2、通过例题和练习突出了本节课的重点。
3、本节课学生还不能灵活地选用公式,要加强练习。 (七)板书设计设计说明谢谢 再见
