北师大版数学九年级下册期末综合练习(无答案)
文档属性
| 名称 | 北师大版数学九年级下册期末综合练习(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 675.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-04 20:33:26 | ||
图片预览


文档简介
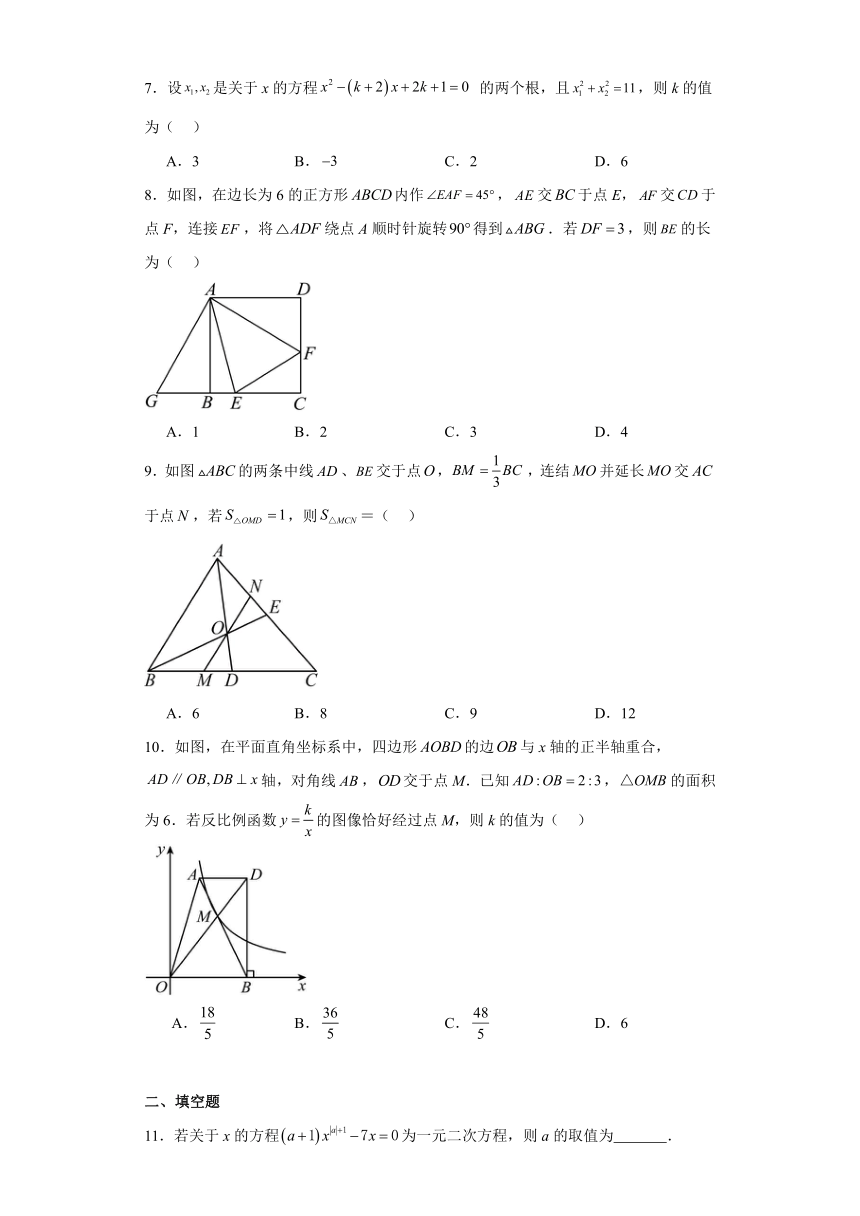
北师大版九年级下册数学期末综合练习
一、单选题
1.在一个不透明的袋子里装有红球、黄球共个,这些球除颜色以外没有任何其他区别,从中任取个球,记下颜色后放回,摇匀.诚诚通过多次试验发现,摸出红球的频率稳定在左右,则袋子中红球的个数最有可能是( ).
A.个 B.个 C.个 D.个
2.下列方程中,关于x的一元二次方程是( )
A. B. C. D.
3.下列几何体中三个视图完全相同的是( )
A. B. C. D.
4.如图,在中,,则的长是( )
A.36 B. C.20 D.15
5.已知是反比例函数,则的值是( )
A. B. C. D.
6.如图,四边形为平行四边形,延长到,使,连接,,,添加一个条件,不能使四边形成为矩形的是( ).
A. B. C. D.
7.设是关于x的方程 的两个根,且,则k的值为( )
A.3 B. C.2 D.6
8.如图,在边长为6的正方形内作,交于点E,交于点F,连接,将绕点A顺时针旋转得到.若,则的长为( )
A.1 B.2 C.3 D.4
9.如图的两条中线、交于点,,连结并延长交于点,若,则=( )
A.6 B.8 C.9 D.12
10.如图,在平面直角坐标系中,四边形的边与x轴的正半轴重合,轴,对角线,交于点M.已知,的面积为6.若反比例函数的图像恰好经过点M,则k的值为( )
A. B. C. D.6
二、填空题
11.若关于x的方程为一元二次方程,则a的取值为 .
12.如图,矩形中,,将沿对折,C点落在M处,交于点E,作于F,则线段 .
13.如图,数学兴趣小组下午测得一根长为的竹竿影长是,同一时刻测量树高时发现树的影子有一部分落在教学楼的墙壁上,测得留在墙壁上的影高,地面上的影长为.请你帮算一下,树高是 .
14.如图,在中,连接,点是上一点,,连接交于点,若,则四边形的面积是 .
15.一个三角形的两边长分别为3和5,第三边长是方程的根,该三角形的周长为 .
三、解答题
16.解方程
(1);
(2).
(3).
17.2021年,“碳中和、碳达峰”成为高频热词.为了解学生对“碳中和、碳达峰”知识的知晓情况,某校团委随机对该校部分学生进行了问卷调查,调查结果共分成四个类别:A表示“从未听说过”,B表示“不太了解”,C表示“比较了解”,D表示“非常了解”.根据调查统计结果,绘制成两种不完整的统计图.请结合统计图,回答下列问题.
(1)参加这次调查的学生总人数为______人;
(2)扇形统计图中,B部分扇形所对应的圆心角度数是______;
(3)将条形统计图补充完整;
(4)现需从D类的4名学生中随机抽取2名作为“碳中和、碳达峰”知识的义务宣讲员,这四人中,1名来自七年级,1名来自八年级,2名来自九年级,请用列表或画树状图的方法,求抽到的2名学生来自不同年级的概率.
18.根据要求完成下列题目:
(1)如图中有 块小正方体;
(2)请在下面方格纸中分别画出它的左视图和俯视图;
(3)用小正方形体搭一个几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则这样的几何最多要个小正方体.
19.已知:如图,在矩形中,对角线、相交于点O,E是中点,连结,过点C作交线段的延长线于点F,连结.
(1)求证:;
(2)试判断四边形是什么四边形,并说明理由.
20.学完了《图形的相似》这一章后,某中学数学实践小组决定利用所学知识去测量一古建筑的高度(如图1).如图2,在地面上取两点,分别竖立两根高为的标杆和,两标杆间隔为,并且古建筑,标杆和在同一竖直平面内,从标杆后退到处,从处观察点,三点成一线;从标杆后退到处,从处观察点,三点也成一线.请根据以上测量数据,帮助实践小组求出该古建筑的高度.
21.某蔬菜生产基地用装有恒温系统的大棚栽培一种新品,如图是某天恒温系统从开始到关闭及关闭后,大棚里温度随时间变化的函数图象,其中段是恒温阶段, 段是双曲线的一部分,请根据图中信息解答下列问题:
(1)求k的值;
(2)恒温系统在一天内保持大棚内温度不低于的时间有多少小时?
22.某水果商场经销一种高档水果,原价每千克50元,连续两次降价后每千克32元,若每次下降的百分率相同.
(1)求每次下降的百分率.
(2)若每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下商场决定采取适当的涨价措施,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,且要尽快减少库存,那么每千克应涨价多少元?
23.如图,反比例函数与一次函数的图象交于点、点.
(1)求这两个函数的解析式;
(2)直接写出不等式的解集;
(3)点E为y轴上一个动点,若,求点E的坐标.
24.如图,在平面直角坐标系中,点,点分别在轴、轴的正半轴上,且满足.
(1)求点、点的坐标;
(2)若点从点出发,以每秒1个单位的速度沿线段由向运动,连接,设的面积为,点的运动时间为秒,求与的函数关系式;
(3)在(2)的条件下,是否存在点,使以点为顶点的三角形与相似?若存在,请直接写出点的坐标;若不存在,请说明理由.
一、单选题
1.在一个不透明的袋子里装有红球、黄球共个,这些球除颜色以外没有任何其他区别,从中任取个球,记下颜色后放回,摇匀.诚诚通过多次试验发现,摸出红球的频率稳定在左右,则袋子中红球的个数最有可能是( ).
A.个 B.个 C.个 D.个
2.下列方程中,关于x的一元二次方程是( )
A. B. C. D.
3.下列几何体中三个视图完全相同的是( )
A. B. C. D.
4.如图,在中,,则的长是( )
A.36 B. C.20 D.15
5.已知是反比例函数,则的值是( )
A. B. C. D.
6.如图,四边形为平行四边形,延长到,使,连接,,,添加一个条件,不能使四边形成为矩形的是( ).
A. B. C. D.
7.设是关于x的方程 的两个根,且,则k的值为( )
A.3 B. C.2 D.6
8.如图,在边长为6的正方形内作,交于点E,交于点F,连接,将绕点A顺时针旋转得到.若,则的长为( )
A.1 B.2 C.3 D.4
9.如图的两条中线、交于点,,连结并延长交于点,若,则=( )
A.6 B.8 C.9 D.12
10.如图,在平面直角坐标系中,四边形的边与x轴的正半轴重合,轴,对角线,交于点M.已知,的面积为6.若反比例函数的图像恰好经过点M,则k的值为( )
A. B. C. D.6
二、填空题
11.若关于x的方程为一元二次方程,则a的取值为 .
12.如图,矩形中,,将沿对折,C点落在M处,交于点E,作于F,则线段 .
13.如图,数学兴趣小组下午测得一根长为的竹竿影长是,同一时刻测量树高时发现树的影子有一部分落在教学楼的墙壁上,测得留在墙壁上的影高,地面上的影长为.请你帮算一下,树高是 .
14.如图,在中,连接,点是上一点,,连接交于点,若,则四边形的面积是 .
15.一个三角形的两边长分别为3和5,第三边长是方程的根,该三角形的周长为 .
三、解答题
16.解方程
(1);
(2).
(3).
17.2021年,“碳中和、碳达峰”成为高频热词.为了解学生对“碳中和、碳达峰”知识的知晓情况,某校团委随机对该校部分学生进行了问卷调查,调查结果共分成四个类别:A表示“从未听说过”,B表示“不太了解”,C表示“比较了解”,D表示“非常了解”.根据调查统计结果,绘制成两种不完整的统计图.请结合统计图,回答下列问题.
(1)参加这次调查的学生总人数为______人;
(2)扇形统计图中,B部分扇形所对应的圆心角度数是______;
(3)将条形统计图补充完整;
(4)现需从D类的4名学生中随机抽取2名作为“碳中和、碳达峰”知识的义务宣讲员,这四人中,1名来自七年级,1名来自八年级,2名来自九年级,请用列表或画树状图的方法,求抽到的2名学生来自不同年级的概率.
18.根据要求完成下列题目:
(1)如图中有 块小正方体;
(2)请在下面方格纸中分别画出它的左视图和俯视图;
(3)用小正方形体搭一个几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则这样的几何最多要个小正方体.
19.已知:如图,在矩形中,对角线、相交于点O,E是中点,连结,过点C作交线段的延长线于点F,连结.
(1)求证:;
(2)试判断四边形是什么四边形,并说明理由.
20.学完了《图形的相似》这一章后,某中学数学实践小组决定利用所学知识去测量一古建筑的高度(如图1).如图2,在地面上取两点,分别竖立两根高为的标杆和,两标杆间隔为,并且古建筑,标杆和在同一竖直平面内,从标杆后退到处,从处观察点,三点成一线;从标杆后退到处,从处观察点,三点也成一线.请根据以上测量数据,帮助实践小组求出该古建筑的高度.
21.某蔬菜生产基地用装有恒温系统的大棚栽培一种新品,如图是某天恒温系统从开始到关闭及关闭后,大棚里温度随时间变化的函数图象,其中段是恒温阶段, 段是双曲线的一部分,请根据图中信息解答下列问题:
(1)求k的值;
(2)恒温系统在一天内保持大棚内温度不低于的时间有多少小时?
22.某水果商场经销一种高档水果,原价每千克50元,连续两次降价后每千克32元,若每次下降的百分率相同.
(1)求每次下降的百分率.
(2)若每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下商场决定采取适当的涨价措施,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,且要尽快减少库存,那么每千克应涨价多少元?
23.如图,反比例函数与一次函数的图象交于点、点.
(1)求这两个函数的解析式;
(2)直接写出不等式的解集;
(3)点E为y轴上一个动点,若,求点E的坐标.
24.如图,在平面直角坐标系中,点,点分别在轴、轴的正半轴上,且满足.
(1)求点、点的坐标;
(2)若点从点出发,以每秒1个单位的速度沿线段由向运动,连接,设的面积为,点的运动时间为秒,求与的函数关系式;
(3)在(2)的条件下,是否存在点,使以点为顶点的三角形与相似?若存在,请直接写出点的坐标;若不存在,请说明理由.
同课章节目录
