3.6 直线和圆的位置关系 第1课时 课件(共22张PPT) 2023-2024学年初中数学北师版九年级下册
文档属性
| 名称 | 3.6 直线和圆的位置关系 第1课时 课件(共22张PPT) 2023-2024学年初中数学北师版九年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 582.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 09:40:24 | ||
图片预览



文档简介
(共22张PPT)
第三章 圆
3.6 直线和圆的位置关系
第1课时
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.理解掌握直线与圆的三种位置关系
2.理解直线与圆三种位置关系的性质,并解决简单问题(重点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
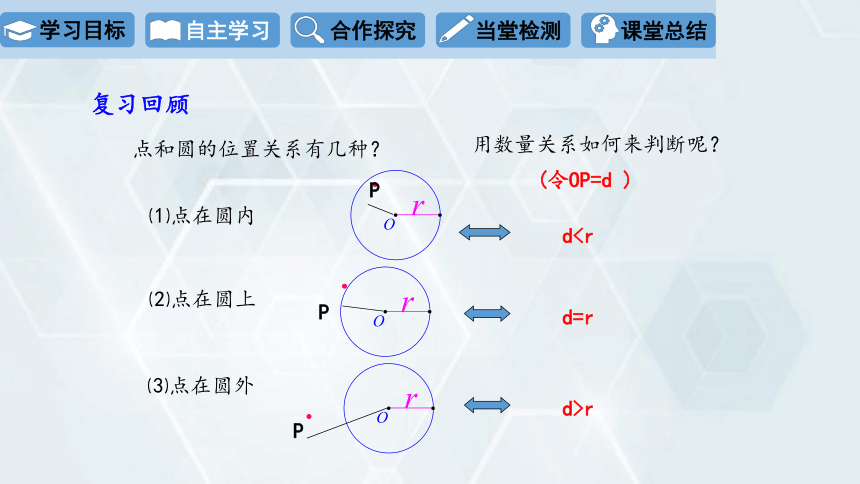
复习回顾
点和圆的位置关系有几种?
dd=r
d>r
用数量关系如何来判断呢?
⑴点在圆内
·
P
⑵点在圆上
·
P
⑶点在圆外
·
P
(令OP=d )
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:用定义判断直线与圆的位置关系
问题1:如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?
合作探究
当堂检测
学习目标
课堂总结
自主学习
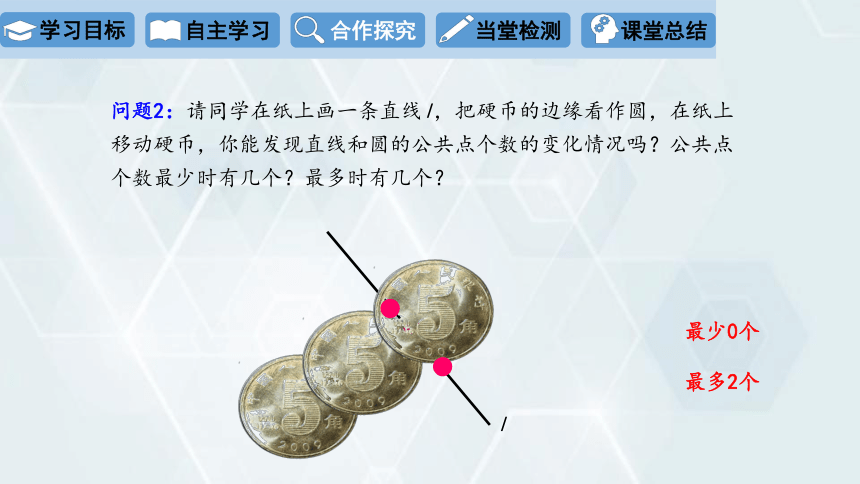
问题2:请同学在纸上画一条直线l,把硬币的边缘看作圆,在纸上移动硬币,你能发现直线和圆的公共点个数的变化情况吗?公共点个数最少时有几个?最多时有几个?
●
●
●
l
最少0个
最多2个
合作探究
当堂检测
学习目标
课堂总结
自主学习
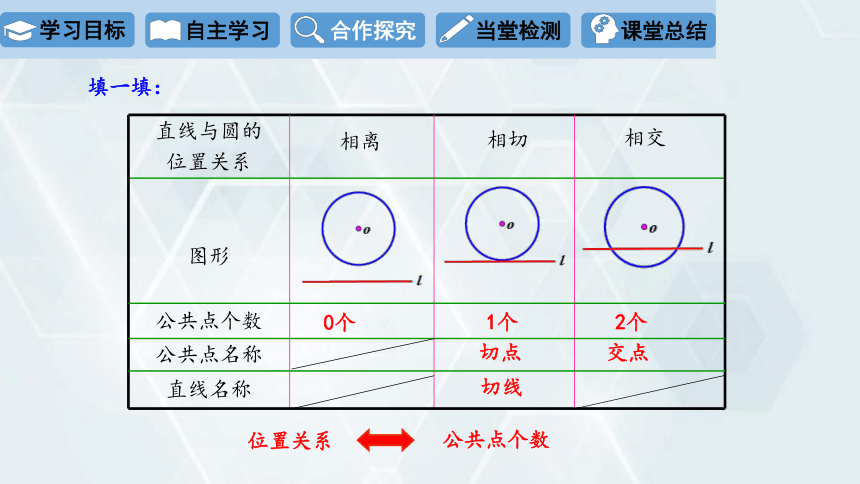
直线与圆的 位置关系
图形
公共点个数
公共点名称
直线名称
2个
交点
1个
切点
切线
0个
相离
相切
相交
位置关系
公共点个数
填一填:
合作探究
当堂检测
学习目标
课堂总结
自主学习
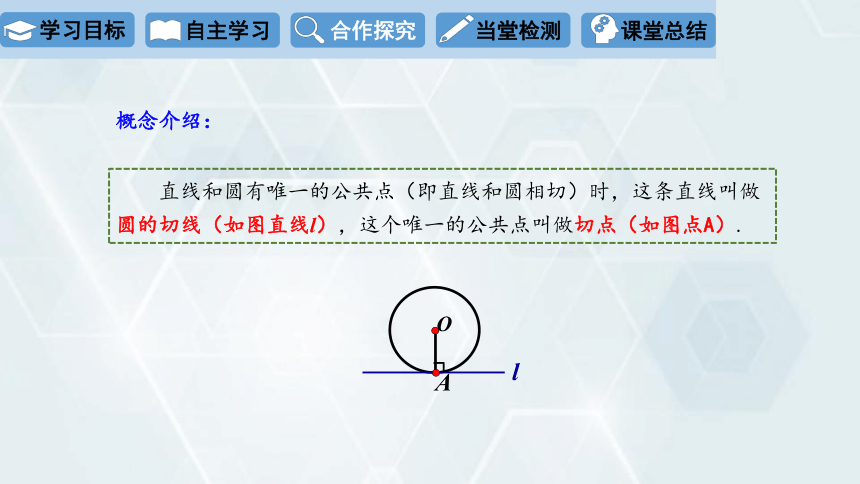
直线和圆有唯一的公共点(即直线和圆相切)时,这条直线叫做圆的切线(如图直线l),这个唯一的公共点叫做切点(如图点A).
A
l
O
概念介绍:
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
.O
.O
.O
.O
.O
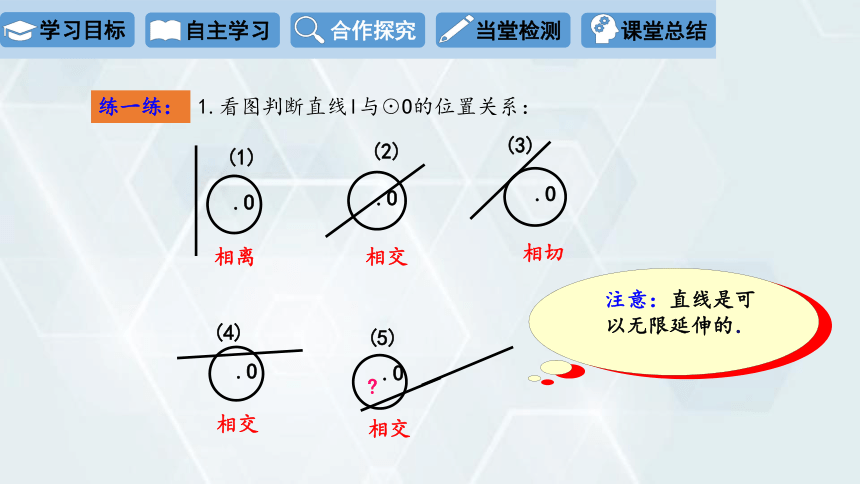
1.看图判断直线l与☉O的位置关系:
(1)
(2)
(3)
(4)
(5)
相离
相交
相切
相交
注意:直线是可以无限延伸的.
相交
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二:用数量关系判断直线与圆的位置关系
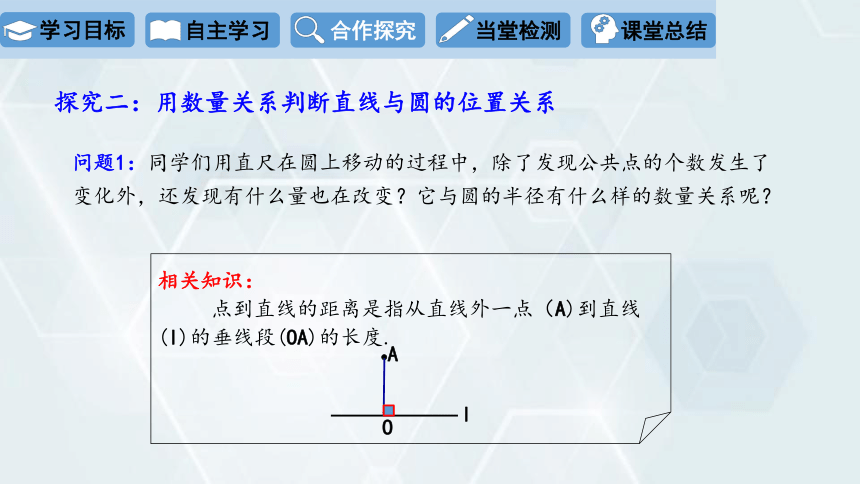
问题1:同学们用直尺在圆上移动的过程中,除了发现公共点的个数发生了变化外,还发现有什么量也在改变?它与圆的半径有什么样的数量关系呢?
相关知识:
点到直线的距离是指从直线外一点(A)到直线(l)的垂线段(OA)的长度.
l
A
O
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题2:怎样用d(圆心与直线的距离)来判别直线与圆的位置关系呢?
O
d
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
r
d
∟
r
d
∟
r
d
数形结合:
位置关系
数量关系
(用圆心O到直线的距离d与圆的半径r的关系来区分)
o
o
o
公共点个数
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.已知圆的半径为6cm,设直线和圆心的距离为d :
(3)若d=8cm ,则直线与圆______, 直线与圆有____个公共点.
(2)若d=6cm ,则直线与圆______, 直线与圆有____个公共点.
(1)若d=4cm ,则直线与圆 , 直线与圆有____个公共点.
(3)若AB和⊙O相交, 则 .
3.已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据条件填写d的范围:
(1)若AB和⊙O相离, 则 ;
(2)若AB和⊙O相切, 则 ;
相交
相切
相离
d > 5cm
d = 5cm
0cm≤d < 5cm
2
1
0
练一练:
合作探究
当堂检测
学习目标
课堂总结
自主学习
知识点:切线的性质
思考:如图,如果直线l是⊙O 的切线,点A为切点,那么OA与l垂直吗?
A
l
O
∵直线l是⊙O 的切线,A是切点.
∴直线l ⊥OA.
切线性质
圆的切线垂直于经过切点的半径.
几何符号表达:
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究三:切线的性质定理的证明
问题提出:如何证明切线的性质定理呢?
问题探究:
证法1:反证法.
小亮的理由是:直径AB与直线CD要么垂直,要么不垂直.
(1)假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,
(2)则OMC
D
B
O
A
(3)所以AB与CD垂直.
M
合作探究
当堂检测
学习目标
课堂总结
自主学习
C
D
O
A
证法2:构造法.
作出小⊙O的同心圆大⊙O,
CD切小⊙O于点A,且A点为CD的中点,
连接OA,根据垂径定理,则CD ⊥OA,
即圆的切线垂直于经过切点的半径.
合作探究
当堂检测
学习目标
课堂总结
自主学习
方法总结:
利用切线的性质解题时,常需连接辅助线,一般连接圆心与切点,构造直角三角形,再利用直角三角形的相关性质解题.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
4.如图, ⊙O切PB于点B,PB=4,PA=2,则⊙O的半径多少?
O
P
B
A
解:连接OB,则∠OBP=90°.
设⊙O的半径为r,则OA=OB=r,
OP=OA+PA=2+r.
在Rt△OBP中,
OB2+PB2=PO2,即r2+42=(2+r)2.
解得 r=3,
即⊙O的半径为3.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.直线和圆相交,圆的半径为r,且圆心到直线的距离为5,则有( )
A. r < 5 B. r > 5 C. r = 5 D. r ≥ 5
B
2.如图,在☉O的内接四边形ABCD中,AB是直径,∠BCD=120°,过D点的切线PD与直线AB交于点P,则∠ADP的度数为( )
A.40° B.35° C.30° D.45°
C
P
O
第2题
D
A
B
C
合作探究
当堂检测
学习目标
课堂总结
自主学习
解析:过点A作AQ⊥MN于Q,连接AN,设半径为r,由垂径定理有MQ=NQ,所以AQ=2,AN=r,NQ=4-r,利用勾股定理可以求出NQ=1.5,所以N点坐标为(-1,-2).故选A.
3.如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点.若点M的坐标是(-4,-2),则点N的坐标为( )
A.(-1,-2) B.(1,2)
C.(-1.5,-2) D.(1.5,-2)
A
合作探究
当堂检测
学习目标
课堂总结
自主学习
4.如图,在Rt△ABC中,∠A=90°,∠B=30°,点O为BC上一点,OB=2,AC=3,以点O为圆心,r为半径的⊙O与△ABC的一边相切,求r的值.
解:∵∠A=90°,∠B=30°,AC=3,
∴BC=2AC=6.
∵OB=2,∴OC=4.
当⊙O与AB相切时,过点O作OD⊥AB于点D,
D
当⊙O与AC相切时,
作OE⊥AC于点E,则OE∥AB,
∴∠COE=∠B=30°,
∴OE= .
综上所述,r的值为1或 .
E
∴OD= OB=1;
∴CE= OC=2,
合作探究
当堂检测
学习目标
课堂总结
自主学习
直线与圆的位置关系
定义
性质
判定
相离
相切
相交
公共点的个数
d与r的数量关系
定义法
性质法
相离:0个
相切:1个
相交:2个
相离:d>r
相切:d=r
相交:d0个:相离;1个:相切;2个:相交
d>r:相离
d=r:相切
d合作探究
当堂检测
学习目标
课堂总结
自主学习
切线的
性质
有1个公共点
d=r
圆的切线垂直于经过切点的半径
有切线时常用辅助线添加方法:
见切线,连切点,得垂直.
性质定理
第三章 圆
3.6 直线和圆的位置关系
第1课时
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.理解掌握直线与圆的三种位置关系
2.理解直线与圆三种位置关系的性质,并解决简单问题(重点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
复习回顾
点和圆的位置关系有几种?
d
d>r
用数量关系如何来判断呢?
⑴点在圆内
·
P
⑵点在圆上
·
P
⑶点在圆外
·
P
(令OP=d )
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:用定义判断直线与圆的位置关系
问题1:如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题2:请同学在纸上画一条直线l,把硬币的边缘看作圆,在纸上移动硬币,你能发现直线和圆的公共点个数的变化情况吗?公共点个数最少时有几个?最多时有几个?
●
●
●
l
最少0个
最多2个
合作探究
当堂检测
学习目标
课堂总结
自主学习
直线与圆的 位置关系
图形
公共点个数
公共点名称
直线名称
2个
交点
1个
切点
切线
0个
相离
相切
相交
位置关系
公共点个数
填一填:
合作探究
当堂检测
学习目标
课堂总结
自主学习
直线和圆有唯一的公共点(即直线和圆相切)时,这条直线叫做圆的切线(如图直线l),这个唯一的公共点叫做切点(如图点A).
A
l
O
概念介绍:
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
.O
.O
.O
.O
.O
1.看图判断直线l与☉O的位置关系:
(1)
(2)
(3)
(4)
(5)
相离
相交
相切
相交
注意:直线是可以无限延伸的.
相交
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二:用数量关系判断直线与圆的位置关系
问题1:同学们用直尺在圆上移动的过程中,除了发现公共点的个数发生了变化外,还发现有什么量也在改变?它与圆的半径有什么样的数量关系呢?
相关知识:
点到直线的距离是指从直线外一点(A)到直线(l)的垂线段(OA)的长度.
l
A
O
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题2:怎样用d(圆心与直线的距离)来判别直线与圆的位置关系呢?
O
d
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:
直线和圆相交
d< r
直线和圆相切
d= r
直线和圆相离
d> r
r
d
∟
r
d
∟
r
d
数形结合:
位置关系
数量关系
(用圆心O到直线的距离d与圆的半径r的关系来区分)
o
o
o
公共点个数
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.已知圆的半径为6cm,设直线和圆心的距离为d :
(3)若d=8cm ,则直线与圆______, 直线与圆有____个公共点.
(2)若d=6cm ,则直线与圆______, 直线与圆有____个公共点.
(1)若d=4cm ,则直线与圆 , 直线与圆有____个公共点.
(3)若AB和⊙O相交, 则 .
3.已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据条件填写d的范围:
(1)若AB和⊙O相离, 则 ;
(2)若AB和⊙O相切, 则 ;
相交
相切
相离
d > 5cm
d = 5cm
0cm≤d < 5cm
2
1
0
练一练:
合作探究
当堂检测
学习目标
课堂总结
自主学习
知识点:切线的性质
思考:如图,如果直线l是⊙O 的切线,点A为切点,那么OA与l垂直吗?
A
l
O
∵直线l是⊙O 的切线,A是切点.
∴直线l ⊥OA.
切线性质
圆的切线垂直于经过切点的半径.
几何符号表达:
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究三:切线的性质定理的证明
问题提出:如何证明切线的性质定理呢?
问题探究:
证法1:反证法.
小亮的理由是:直径AB与直线CD要么垂直,要么不垂直.
(1)假设AB与CD不垂直,过点O作一条直径垂直于CD,垂足为M,
(2)则OM
D
B
O
A
(3)所以AB与CD垂直.
M
合作探究
当堂检测
学习目标
课堂总结
自主学习
C
D
O
A
证法2:构造法.
作出小⊙O的同心圆大⊙O,
CD切小⊙O于点A,且A点为CD的中点,
连接OA,根据垂径定理,则CD ⊥OA,
即圆的切线垂直于经过切点的半径.
合作探究
当堂检测
学习目标
课堂总结
自主学习
方法总结:
利用切线的性质解题时,常需连接辅助线,一般连接圆心与切点,构造直角三角形,再利用直角三角形的相关性质解题.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
4.如图, ⊙O切PB于点B,PB=4,PA=2,则⊙O的半径多少?
O
P
B
A
解:连接OB,则∠OBP=90°.
设⊙O的半径为r,则OA=OB=r,
OP=OA+PA=2+r.
在Rt△OBP中,
OB2+PB2=PO2,即r2+42=(2+r)2.
解得 r=3,
即⊙O的半径为3.
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.直线和圆相交,圆的半径为r,且圆心到直线的距离为5,则有( )
A. r < 5 B. r > 5 C. r = 5 D. r ≥ 5
B
2.如图,在☉O的内接四边形ABCD中,AB是直径,∠BCD=120°,过D点的切线PD与直线AB交于点P,则∠ADP的度数为( )
A.40° B.35° C.30° D.45°
C
P
O
第2题
D
A
B
C
合作探究
当堂检测
学习目标
课堂总结
自主学习
解析:过点A作AQ⊥MN于Q,连接AN,设半径为r,由垂径定理有MQ=NQ,所以AQ=2,AN=r,NQ=4-r,利用勾股定理可以求出NQ=1.5,所以N点坐标为(-1,-2).故选A.
3.如图,在平面直角坐标系中,⊙A与y轴相切于原点O,平行于x轴的直线交⊙A于M、N两点.若点M的坐标是(-4,-2),则点N的坐标为( )
A.(-1,-2) B.(1,2)
C.(-1.5,-2) D.(1.5,-2)
A
合作探究
当堂检测
学习目标
课堂总结
自主学习
4.如图,在Rt△ABC中,∠A=90°,∠B=30°,点O为BC上一点,OB=2,AC=3,以点O为圆心,r为半径的⊙O与△ABC的一边相切,求r的值.
解:∵∠A=90°,∠B=30°,AC=3,
∴BC=2AC=6.
∵OB=2,∴OC=4.
当⊙O与AB相切时,过点O作OD⊥AB于点D,
D
当⊙O与AC相切时,
作OE⊥AC于点E,则OE∥AB,
∴∠COE=∠B=30°,
∴OE= .
综上所述,r的值为1或 .
E
∴OD= OB=1;
∴CE= OC=2,
合作探究
当堂检测
学习目标
课堂总结
自主学习
直线与圆的位置关系
定义
性质
判定
相离
相切
相交
公共点的个数
d与r的数量关系
定义法
性质法
相离:0个
相切:1个
相交:2个
相离:d>r
相切:d=r
相交:d
d>r:相离
d=r:相切
d
当堂检测
学习目标
课堂总结
自主学习
切线的
性质
有1个公共点
d=r
圆的切线垂直于经过切点的半径
有切线时常用辅助线添加方法:
见切线,连切点,得垂直.
性质定理
