3.4 圆周角和圆心角的关系 第1课时 课件(共17张PPT) 2023-2024学年初中数学北师版九年级下册
文档属性
| 名称 | 3.4 圆周角和圆心角的关系 第1课时 课件(共17张PPT) 2023-2024学年初中数学北师版九年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 09:40:59 | ||
图片预览


文档简介
(共17张PPT)
第三章 圆
3.4 圆周角和圆心角的关系
第1课时
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.理解圆周角的概念,会叙述并证明圆周角定理.
2.理解圆周角与圆心角的关系并能运用圆周角定理及推论解决简单的几何问题.(重点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
复习回顾:
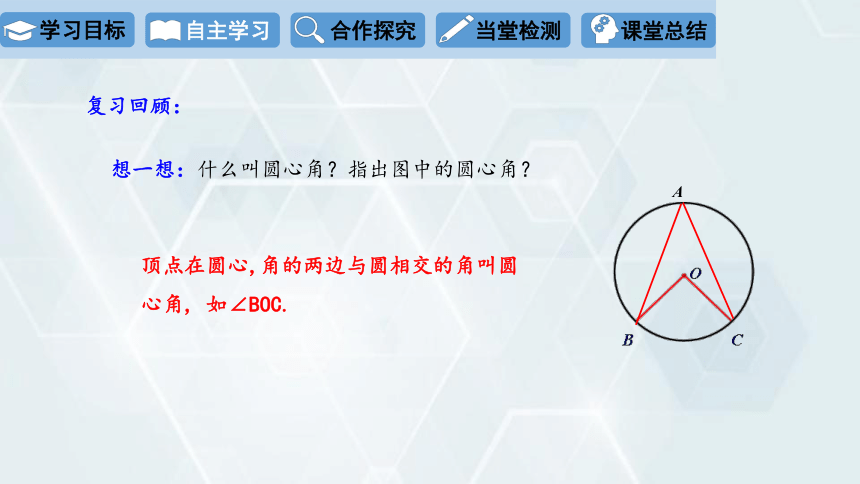
想一想:什么叫圆心角?指出图中的圆心角?
顶点在圆心,角的两边与圆相交的角叫圆心角, 如∠BOC.
A
合作探究
当堂检测
学习目标
课堂总结
自主学习
知识点:圆周角的定义
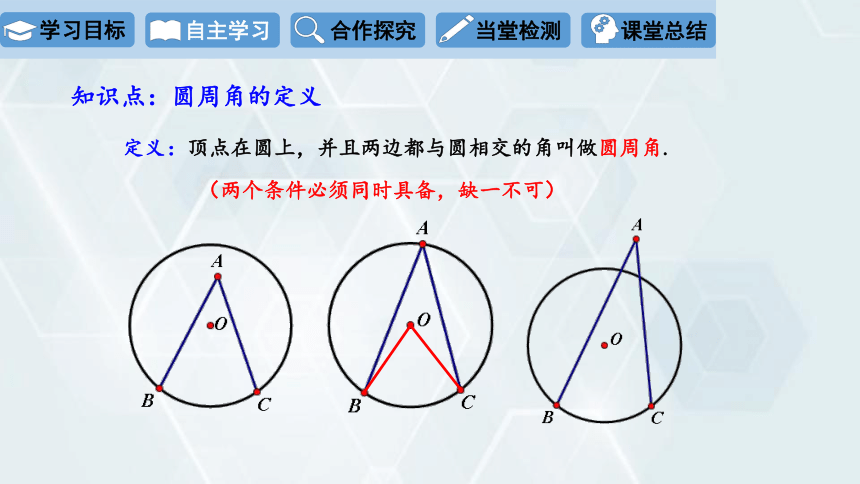
定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角.
(两个条件必须同时具备,缺一不可)
合作探究
当堂检测
学习目标
课堂总结
自主学习
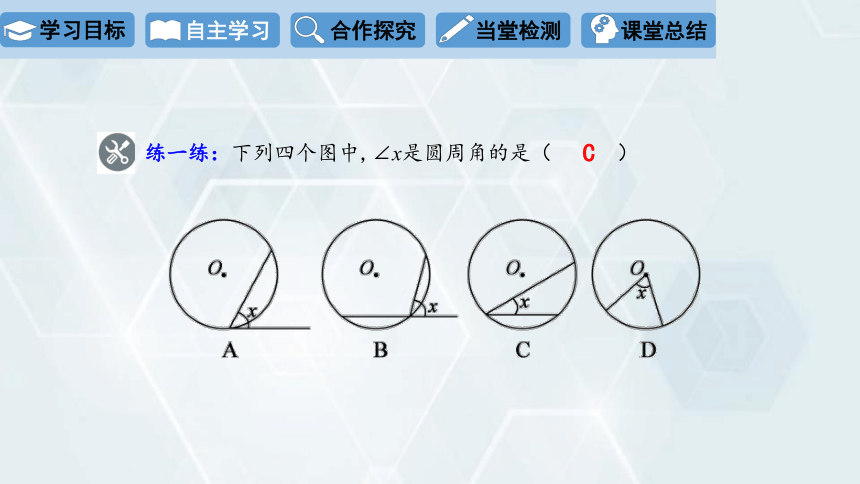
练一练:下列四个图中,∠x是圆周角的是( )
C
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究:圆周角定理及推论1
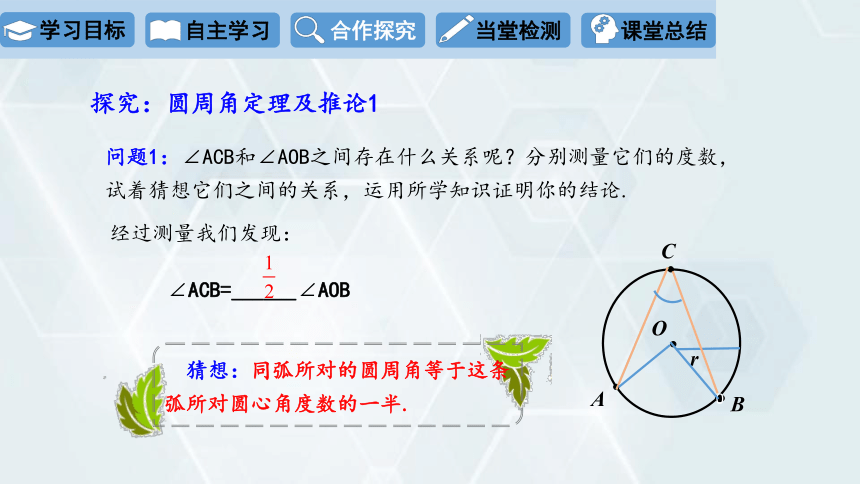
问题1:∠ACB和∠AOB之间存在什么关系呢?分别测量它们的度数,试着猜想它们之间的关系,运用所学知识证明你的结论.
O
r
0
B
A
C
∠ACB=______∠AOB
经过测量我们发现:
猜想:同弧所对的圆周角等于这条弧所对圆心角度数的一半.
合作探究
当堂检测
学习目标
课堂总结
自主学习
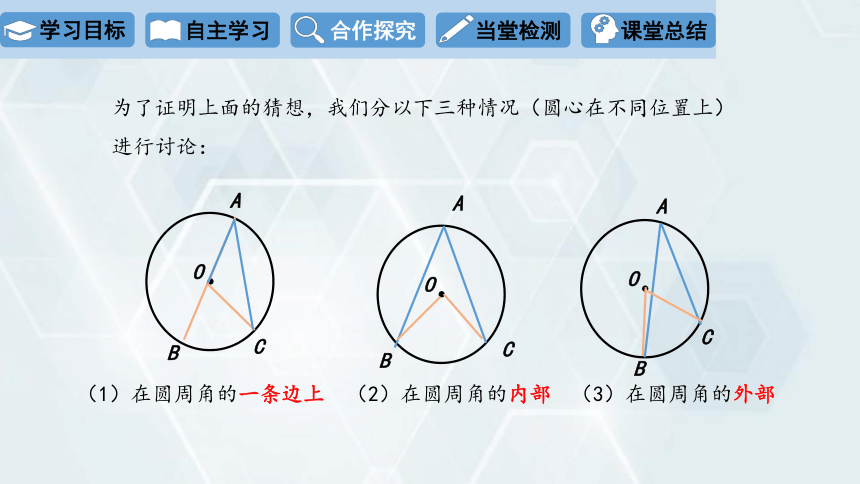
为了证明上面的猜想,我们分以下三种情况(圆心在不同位置上)进行讨论:
(1)在圆周角的一条边上
(2)在圆周角的内部
(3)在圆周角的外部
O
B
A
C
O
B
A
C
O
B
A
C
合作探究
当堂检测
学习目标
课堂总结
自主学习
(1)圆心在圆周角的一条边上
O
B
A
C
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
∠A=______∠BOC
合作探究
当堂检测
学习目标
课堂总结
自主学习
(2)圆心在圆周角的内部
O
B
A
C
D
OA=OB=OC
2∠BAD= ∠BOD,
2∠CAD= ∠COD,
∠BOC= ∠ BOD+ ∠COD
∠A=______∠BOC
合作探究
当堂检测
学习目标
课堂总结
自主学习
(3)圆心在圆周角的外部
O
B
A
C
D
OA=OB=OC
∠DOB=2∠OAB
∠DOC=2∠OAC
∠BOC= ∠ DOC- ∠DOB
∠A=______∠BOC
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:
圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半.
O
0
B
A
C
合作探究
当堂检测
学习目标
课堂总结
自主学习
思考:根据圆的对称性的相关知识,你能由圆周角定理得出什么推论吗?
推论1:同弧或等弧所对的圆周角相等.
O
0
B
A
C
O'
0
B'
A'
C'
合作探究
当堂检测
学习目标
课堂总结
自主学习
已知: 如图,三角形ABC内接于圆, ∠ACB=2∠ABC,点D平分弧AB. 求证: AC=BD
A
B
C
D
练一练:
证明: 连接CD
(同圆或等圆中,同弧或等弧所对的圆周角相等)
∴ ∠ABC=∠BCD
(同圆或等圆中,相等的圆周角所对的弧也相等)
∵ AD=BD
(
(
∴ AC=BD
(
(
∴ AC=BD
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.如图,AB是⊙O的直径,C、D、E是⊙O上的点,则∠1+∠2等于( )
A.90° B.45° C.180° D.60°
A
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.已知△ABC的三个顶点在⊙O上,∠BAC=50°,∠ABC=47°, 则∠AOB= .
B
A
C
O
166°
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.船在航行过程中,船长通过测定角度数来确定是否遇到暗礁,如图,A、B表示灯塔,暗礁分布在经过A、B两点的一个圆形区域内,优弧AB上任一点C都是有触礁危险的临界点,∠ACB就是“危险角”,当船位于安全区域时,∠α与“危险角”有怎样的大小关系?
解:如图,∠APB交优弧AB于点E,连接EB,
由圆周角定理知,∠AEB=∠ACB,
∵∠AEB是△PEB的一个外角,∴∠AEB>∠P,
∴当∠α<∠ACB时船不进入暗礁区.
∴当船位于安全区域时,它与两个灯塔的夹角∠α小于“危险角”.
合作探究
当堂检测
学习目标
课堂总结
自主学习
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆周角定理的推论1
圆周角的度数等于它所对弧上的圆心角度数的一半
同弧或等弧所对的圆周角相等
1.顶点在圆上,2.两边都与圆相交的角
第三章 圆
3.4 圆周角和圆心角的关系
第1课时
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.理解圆周角的概念,会叙述并证明圆周角定理.
2.理解圆周角与圆心角的关系并能运用圆周角定理及推论解决简单的几何问题.(重点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
复习回顾:
想一想:什么叫圆心角?指出图中的圆心角?
顶点在圆心,角的两边与圆相交的角叫圆心角, 如∠BOC.
A
合作探究
当堂检测
学习目标
课堂总结
自主学习
知识点:圆周角的定义
定义:顶点在圆上,并且两边都与圆相交的角叫做圆周角.
(两个条件必须同时具备,缺一不可)
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:下列四个图中,∠x是圆周角的是( )
C
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究:圆周角定理及推论1
问题1:∠ACB和∠AOB之间存在什么关系呢?分别测量它们的度数,试着猜想它们之间的关系,运用所学知识证明你的结论.
O
r
0
B
A
C
∠ACB=______∠AOB
经过测量我们发现:
猜想:同弧所对的圆周角等于这条弧所对圆心角度数的一半.
合作探究
当堂检测
学习目标
课堂总结
自主学习
为了证明上面的猜想,我们分以下三种情况(圆心在不同位置上)进行讨论:
(1)在圆周角的一条边上
(2)在圆周角的内部
(3)在圆周角的外部
O
B
A
C
O
B
A
C
O
B
A
C
合作探究
当堂检测
学习目标
课堂总结
自主学习
(1)圆心在圆周角的一条边上
O
B
A
C
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
∠A=______∠BOC
合作探究
当堂检测
学习目标
课堂总结
自主学习
(2)圆心在圆周角的内部
O
B
A
C
D
OA=OB=OC
2∠BAD= ∠BOD,
2∠CAD= ∠COD,
∠BOC= ∠ BOD+ ∠COD
∠A=______∠BOC
合作探究
当堂检测
学习目标
课堂总结
自主学习
(3)圆心在圆周角的外部
O
B
A
C
D
OA=OB=OC
∠DOB=2∠OAB
∠DOC=2∠OAC
∠BOC= ∠ DOC- ∠DOB
∠A=______∠BOC
合作探究
当堂检测
学习目标
课堂总结
自主学习
归纳总结:
圆周角定理:
圆周角的度数等于它所对弧上的圆心角度数的一半.
O
0
B
A
C
合作探究
当堂检测
学习目标
课堂总结
自主学习
思考:根据圆的对称性的相关知识,你能由圆周角定理得出什么推论吗?
推论1:同弧或等弧所对的圆周角相等.
O
0
B
A
C
O'
0
B'
A'
C'
合作探究
当堂检测
学习目标
课堂总结
自主学习
已知: 如图,三角形ABC内接于圆, ∠ACB=2∠ABC,点D平分弧AB. 求证: AC=BD
A
B
C
D
练一练:
证明: 连接CD
(同圆或等圆中,同弧或等弧所对的圆周角相等)
∴ ∠ABC=∠BCD
(同圆或等圆中,相等的圆周角所对的弧也相等)
∵ AD=BD
(
(
∴ AC=BD
(
(
∴ AC=BD
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.如图,AB是⊙O的直径,C、D、E是⊙O上的点,则∠1+∠2等于( )
A.90° B.45° C.180° D.60°
A
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.已知△ABC的三个顶点在⊙O上,∠BAC=50°,∠ABC=47°, 则∠AOB= .
B
A
C
O
166°
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.船在航行过程中,船长通过测定角度数来确定是否遇到暗礁,如图,A、B表示灯塔,暗礁分布在经过A、B两点的一个圆形区域内,优弧AB上任一点C都是有触礁危险的临界点,∠ACB就是“危险角”,当船位于安全区域时,∠α与“危险角”有怎样的大小关系?
解:如图,∠APB交优弧AB于点E,连接EB,
由圆周角定理知,∠AEB=∠ACB,
∵∠AEB是△PEB的一个外角,∴∠AEB>∠P,
∴当∠α<∠ACB时船不进入暗礁区.
∴当船位于安全区域时,它与两个灯塔的夹角∠α小于“危险角”.
合作探究
当堂检测
学习目标
课堂总结
自主学习
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆周角定理的推论1
圆周角的度数等于它所对弧上的圆心角度数的一半
同弧或等弧所对的圆周角相等
1.顶点在圆上,2.两边都与圆相交的角
