3.7 切线长定理 课件(共15张PPT) 2023-2024学年初中数学北师版九年级下册
文档属性
| 名称 | 3.7 切线长定理 课件(共15张PPT) 2023-2024学年初中数学北师版九年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 458.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-06 09:41:48 | ||
图片预览



文档简介
(共15张PPT)
第三章 圆
3.7 切线长定理
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.理解切线长的概念;
2.掌握切线长定理,初步学会运用切线长定理进行计算与证明.(重点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
P
O
B
A
1.如图所示,直线AB和半径为r的圆O的位置关系是________,有_______个交点。点到圆心的距离OP=_____
相切
1
r
2.同学们玩过悠悠球吗?悠悠球的旋转的那一瞬间,
你能从中抽象出什么样数学图形?
合作探究
当堂检测
学习目标
课堂总结
自主学习
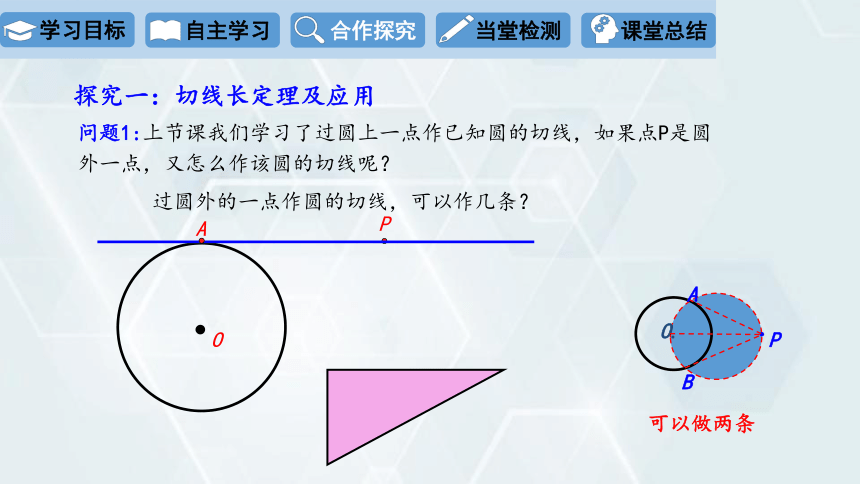
探究一:切线长定理及应用
问题1:上节课我们学习了过圆上一点作已知圆的切线,如果点P是圆外一点,又怎么作该圆的切线呢?
O.
P
A
B
P
O
A
可以做两条
过圆外的一点作圆的切线,可以作几条?
●
合作探究
当堂检测
学习目标
课堂总结
自主学习
P
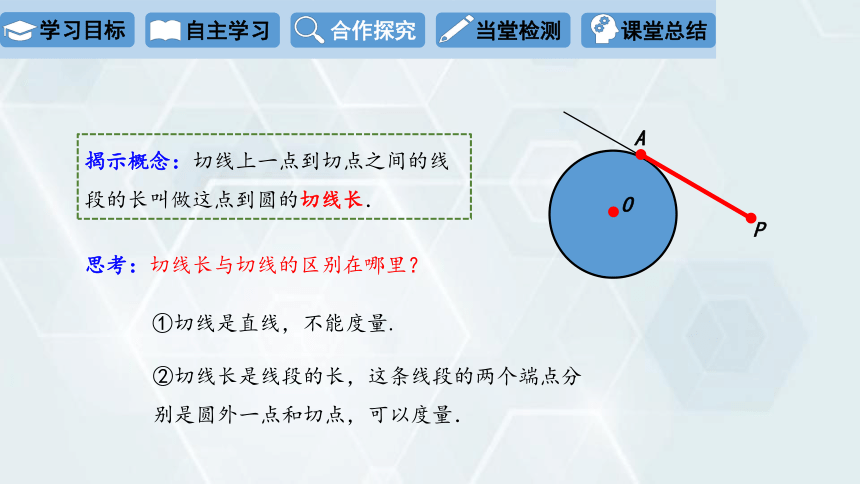
揭示概念:切线上一点到切点之间的线段的长叫做这点到圆的切线长.
A
O
①切线是直线,不能度量.
②切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
思考:切线长与切线的区别在哪里?
合作探究
当堂检测
学习目标
课堂总结
自主学习
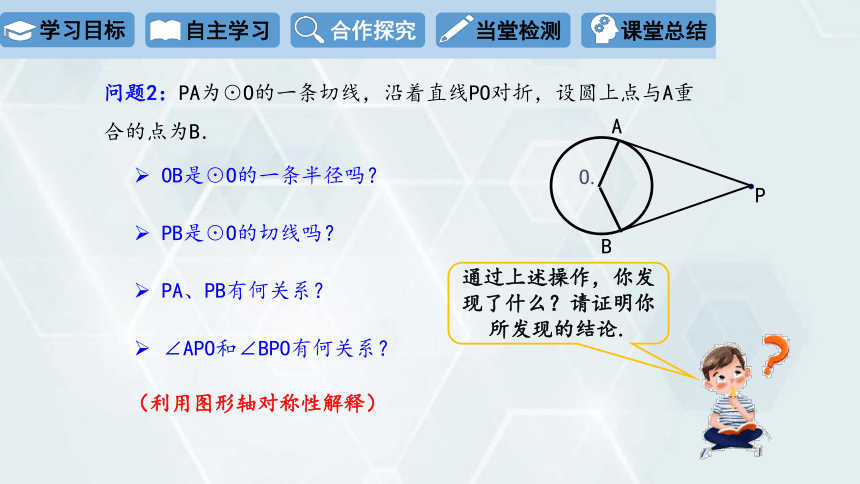
问题2:PA为☉O的一条切线,沿着直线PO对折,设圆上点与A重合的点为B.
OB是☉O的一条半径吗?
PB是☉O的切线吗?
(利用图形轴对称性解释)
PA、PB有何关系?
∠APO和∠BPO有何关系?
O.
P
A
B
通过上述操作,你发现了什么?请证明你所发现的结论.
合作探究
当堂检测
学习目标
课堂总结
自主学习
A
P
O
B
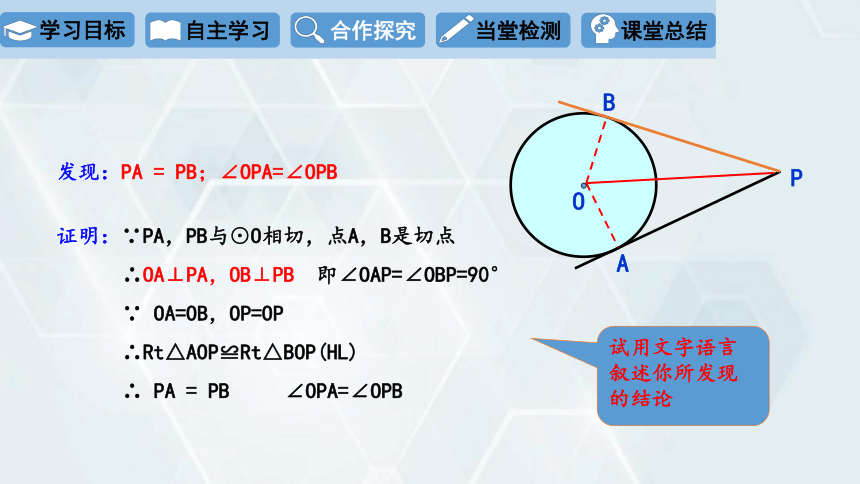
发现:PA = PB;∠OPA=∠OPB
证明:∵PA,PB与⊙O相切,点A,B是切点
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB ∠OPA=∠OPB
试用文字语言叙述你所发现的结论
合作探究
当堂检测
学习目标
课堂总结
自主学习
B
P
O
A
切线长定理:
过圆外一点所画的圆的两条切线的切线长相等.
PA、PB分别切☉O于A、B
PA = PB
∠OPA=∠OPB
几何语言:
切线长定理为证明线段相等、角相等提供了新的方法.
注意
归纳总结:
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
⑴ △PDE的周长是 ;
如图,PA、PB是☉O的两条切线,点A、B是切点,在弧AB上任取一点C,过点C作☉O的切线,分别交PA、PB于点D、E.已知PA=7,∠P=40°.则
O
P
A
B
C
E
D
解析:连接OA、OB、OC、OD和OE.
∵PA、PB是☉O的两条切线,点A、B是切点,∴PA=PB=7.∠PAO=∠PBO=90°.
∠AOB=360°-∠PAO-∠PBO-∠P=140°.
14
又∵DC、DA是☉O的两条切线,点C、A是切点,∴DC=DA.同理可得CE=EB.
l△PDE=PD+DE+PE=PD+DC+CE+PE=PA+PB=14.
合作探究
当堂检测
学习目标
课堂总结
自主学习
如图,PA、PB是☉O的两条切线,点A、B是切点,在弧AB上任取一点C,过点C作☉O的切线,分别交PA、PB于点D、E.已知PA=7,∠P=40°.则⑵ ∠DOE= .
O
P
A
B
C
E
D
解:∵OA=OC,OD=OD,∴△AOD≌△COD,
∴∠DOC=∠DOA= ∠AOC.
同理可得∠COE= ∠COB.
∠DOE=∠DOC+∠COE
= (∠AOC+∠COB)=70°.
70°
合作探究
当堂检测
学习目标
课堂总结
自主学习
切线长问题辅助线添加方法
(3)连接圆心和圆外一点.
(2)连接两切点;
(1)分别连接圆心和切点;
方法归纳
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.如图,PA、PB是☉O的两条切线,切点分别是A、B,如果AP=4, ∠APB= 40 ° ,则∠APO= ,PB= .
B
P
O
A
第1题
20 °
4
合作探究
当堂检测
学习目标
课堂总结
自主学习
E
A
Q
P
F
B
O
∴△PEF周长为24cm
解:∵PA、PB、EF为切线
∴EQ=EA, FQ=FB,PA=PB
∴ PE+EQ=PA=12cm
PF+FQ=PB=PA=12cm
2.已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为 上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12CM,求△PEF的周长.
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.如图,在△ABC中,已知∠ABC=90°,在AB上取一点E,以BE为直径的☉O恰与AC相切于点D,若AE=2,AD=4.
(1)求☉O的直径BE的长.(2)计算△ABC的面积.
解:(1)连接OD,
∴OD⊥AC,∴△ODA是直角三角形,设☉O半径为r,
∴AO=r+2,∴(r+2)2—r2=16,
解得:r=3,∴BE=6.
(2)∵∠ABC=90°,∴OB⊥BC,∴BC是☉O的切线.
∵CD切☉O于D,∴CB=CD,令CB=x,
∴AC=x+4,AB=8.
∴S△ABC= ×8×6=24.
∵x2+82=(x+4)2,∴x=6,
合作探究
当堂检测
学习目标
课堂总结
自主学习
切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
A
P
O
。
B
E
C
D
切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用.
第三章 圆
3.7 切线长定理
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.理解切线长的概念;
2.掌握切线长定理,初步学会运用切线长定理进行计算与证明.(重点)
合作探究
当堂检测
学习目标
课堂总结
自主学习
P
O
B
A
1.如图所示,直线AB和半径为r的圆O的位置关系是________,有_______个交点。点到圆心的距离OP=_____
相切
1
r
2.同学们玩过悠悠球吗?悠悠球的旋转的那一瞬间,
你能从中抽象出什么样数学图形?
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一:切线长定理及应用
问题1:上节课我们学习了过圆上一点作已知圆的切线,如果点P是圆外一点,又怎么作该圆的切线呢?
O.
P
A
B
P
O
A
可以做两条
过圆外的一点作圆的切线,可以作几条?
●
合作探究
当堂检测
学习目标
课堂总结
自主学习
P
揭示概念:切线上一点到切点之间的线段的长叫做这点到圆的切线长.
A
O
①切线是直线,不能度量.
②切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
思考:切线长与切线的区别在哪里?
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题2:PA为☉O的一条切线,沿着直线PO对折,设圆上点与A重合的点为B.
OB是☉O的一条半径吗?
PB是☉O的切线吗?
(利用图形轴对称性解释)
PA、PB有何关系?
∠APO和∠BPO有何关系?
O.
P
A
B
通过上述操作,你发现了什么?请证明你所发现的结论.
合作探究
当堂检测
学习目标
课堂总结
自主学习
A
P
O
B
发现:PA = PB;∠OPA=∠OPB
证明:∵PA,PB与⊙O相切,点A,B是切点
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB ∠OPA=∠OPB
试用文字语言叙述你所发现的结论
合作探究
当堂检测
学习目标
课堂总结
自主学习
B
P
O
A
切线长定理:
过圆外一点所画的圆的两条切线的切线长相等.
PA、PB分别切☉O于A、B
PA = PB
∠OPA=∠OPB
几何语言:
切线长定理为证明线段相等、角相等提供了新的方法.
注意
归纳总结:
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练:
⑴ △PDE的周长是 ;
如图,PA、PB是☉O的两条切线,点A、B是切点,在弧AB上任取一点C,过点C作☉O的切线,分别交PA、PB于点D、E.已知PA=7,∠P=40°.则
O
P
A
B
C
E
D
解析:连接OA、OB、OC、OD和OE.
∵PA、PB是☉O的两条切线,点A、B是切点,∴PA=PB=7.∠PAO=∠PBO=90°.
∠AOB=360°-∠PAO-∠PBO-∠P=140°.
14
又∵DC、DA是☉O的两条切线,点C、A是切点,∴DC=DA.同理可得CE=EB.
l△PDE=PD+DE+PE=PD+DC+CE+PE=PA+PB=14.
合作探究
当堂检测
学习目标
课堂总结
自主学习
如图,PA、PB是☉O的两条切线,点A、B是切点,在弧AB上任取一点C,过点C作☉O的切线,分别交PA、PB于点D、E.已知PA=7,∠P=40°.则⑵ ∠DOE= .
O
P
A
B
C
E
D
解:∵OA=OC,OD=OD,∴△AOD≌△COD,
∴∠DOC=∠DOA= ∠AOC.
同理可得∠COE= ∠COB.
∠DOE=∠DOC+∠COE
= (∠AOC+∠COB)=70°.
70°
合作探究
当堂检测
学习目标
课堂总结
自主学习
切线长问题辅助线添加方法
(3)连接圆心和圆外一点.
(2)连接两切点;
(1)分别连接圆心和切点;
方法归纳
合作探究
当堂检测
学习目标
课堂总结
自主学习
1.如图,PA、PB是☉O的两条切线,切点分别是A、B,如果AP=4, ∠APB= 40 ° ,则∠APO= ,PB= .
B
P
O
A
第1题
20 °
4
合作探究
当堂检测
学习目标
课堂总结
自主学习
E
A
Q
P
F
B
O
∴△PEF周长为24cm
解:∵PA、PB、EF为切线
∴EQ=EA, FQ=FB,PA=PB
∴ PE+EQ=PA=12cm
PF+FQ=PB=PA=12cm
2.已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为 上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12CM,求△PEF的周长.
合作探究
当堂检测
学习目标
课堂总结
自主学习
3.如图,在△ABC中,已知∠ABC=90°,在AB上取一点E,以BE为直径的☉O恰与AC相切于点D,若AE=2,AD=4.
(1)求☉O的直径BE的长.(2)计算△ABC的面积.
解:(1)连接OD,
∴OD⊥AC,∴△ODA是直角三角形,设☉O半径为r,
∴AO=r+2,∴(r+2)2—r2=16,
解得:r=3,∴BE=6.
(2)∵∠ABC=90°,∴OB⊥BC,∴BC是☉O的切线.
∵CD切☉O于D,∴CB=CD,令CB=x,
∴AC=x+4,AB=8.
∴S△ABC= ×8×6=24.
∵x2+82=(x+4)2,∴x=6,
合作探究
当堂检测
学习目标
课堂总结
自主学习
切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.
A
P
O
。
B
E
C
D
切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用.
