第三章 圆单元测试卷B(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
北师大版九年级数学下册《圆》测试卷B
满分:120分 考试时间:90分钟
选择题。(每小题3分,共30分)
1.下列说法中,正确的是( )
A.相等的圆心角所对的弧相等 B.过任意三点可以画一个圆
C.周长相等的圆是等圆 D.平分弦的直径垂直于弦
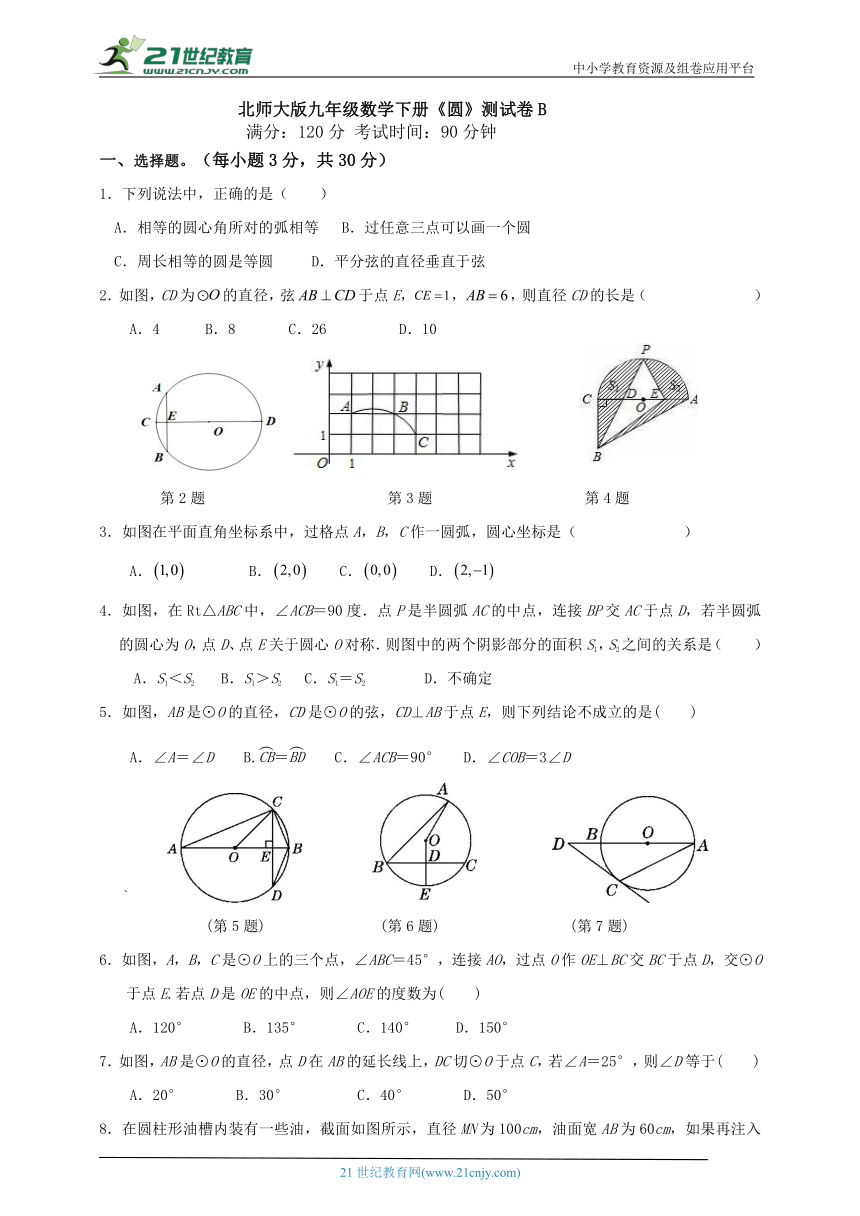
2.如图,CD为的直径,弦于点E,,,则直径CD的长是( )
A.4 B.8 C.26 D.10
第2题 第3题 第4题
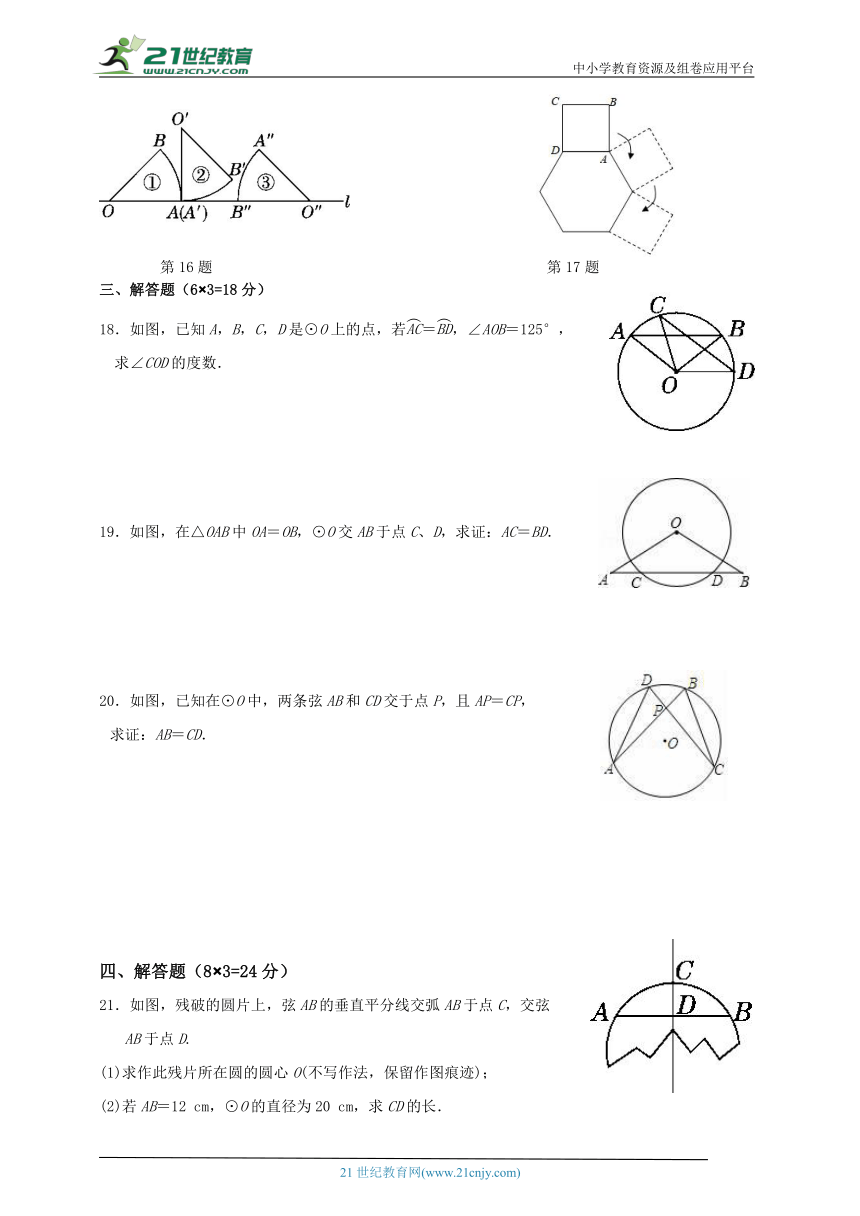
3.如图在平面直角坐标系中,过格点A,B,C作一圆弧,圆心坐标是( )
A. B. C. D.
4.如图,在Rt△ABC中,∠ACB=90度.点P是半圆弧AC的中点,连接BP交AC于点D,若半圆弧的圆心为O,点D、点E关于圆心O对称.则图中的两个阴影部分的面积S1,S2之间的关系是( )
A.S1<S2 B.S1>S2 C.S1=S2 D.不确定
5.如图,AB是⊙O的直径,CD是⊙O的弦,CD⊥AB于点E,则下列结论不成立的是( )
A.∠A=∠D B.= C.∠ACB=90° D.∠COB=3∠D
`
(第5题) (第6题) (第7题)
6.如图,A,B,C是⊙O上的三个点,∠ABC=45°,连接AO,过点O作OE⊥BC交BC于点D,交⊙O于点E.若点D是OE的中点,则∠AOE的度数为( )
A.120° B.135° C.140° D.150°
7.如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A=25°,则∠D等于( )
A.20° B.30° C.40° D.50°
8.在圆柱形油槽内装有一些油,截面如图所示,直径MN为100cm,油面宽AB为60cm,如果再注入一些油后,油面宽变为80cm,则油面上升( )
A.70cm B.10cm或70cm C.10cm D.5cm或35cm
9.如图,弦CD与直径AB相交,连接BC、BD,若∠ABC=50°,则∠BDC=( )
A.20° B.30° C.40° D.50°
第8题 第9题 第10题
10.如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为( )
A. B. C.1 D.2
填空题(每小题4分共28分)
11.在⊙O中,弦AB的长恰好等于半径,弦AB所对的圆心角为 .
12.如图,OA、OB是⊙O的半径,C是⊙O上一点,∠AOB=40°,∠OBC=50°,则∠OAC= °.
第12题 第13题 第14题
13. 小华为了求出一个圆盘的半径,他用所学的知识,将一宽度为2 cm的刻度尺的一边与圆盘相切,另一边与圆盘边缘两个交点处的读数分别是“4”和“16”(单位:cm),如图所示,请你帮小华算出圆盘的半径是 cm.
14. 如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为 .
一圆锥的侧面展开图的圆心角为,底面半径为3,则该圆锥的侧面积为_______.
16.放置在直线l上的扇形AOB,先由位置①滚动(无滑动)到位置②,再由位置②滚动到位置③,如图所示.若半径OA=2,∠AOB=45°,则点O滚动的路径长为________.
17.如图,边长为2的正方形ABCD在等边长的正六边形外部做顺时针滚动,滚动一周回到初始位置时停止,点A在滚动过程中到出发点的最大距离是______.
第16题 第17题
解答题(6×3=18分)
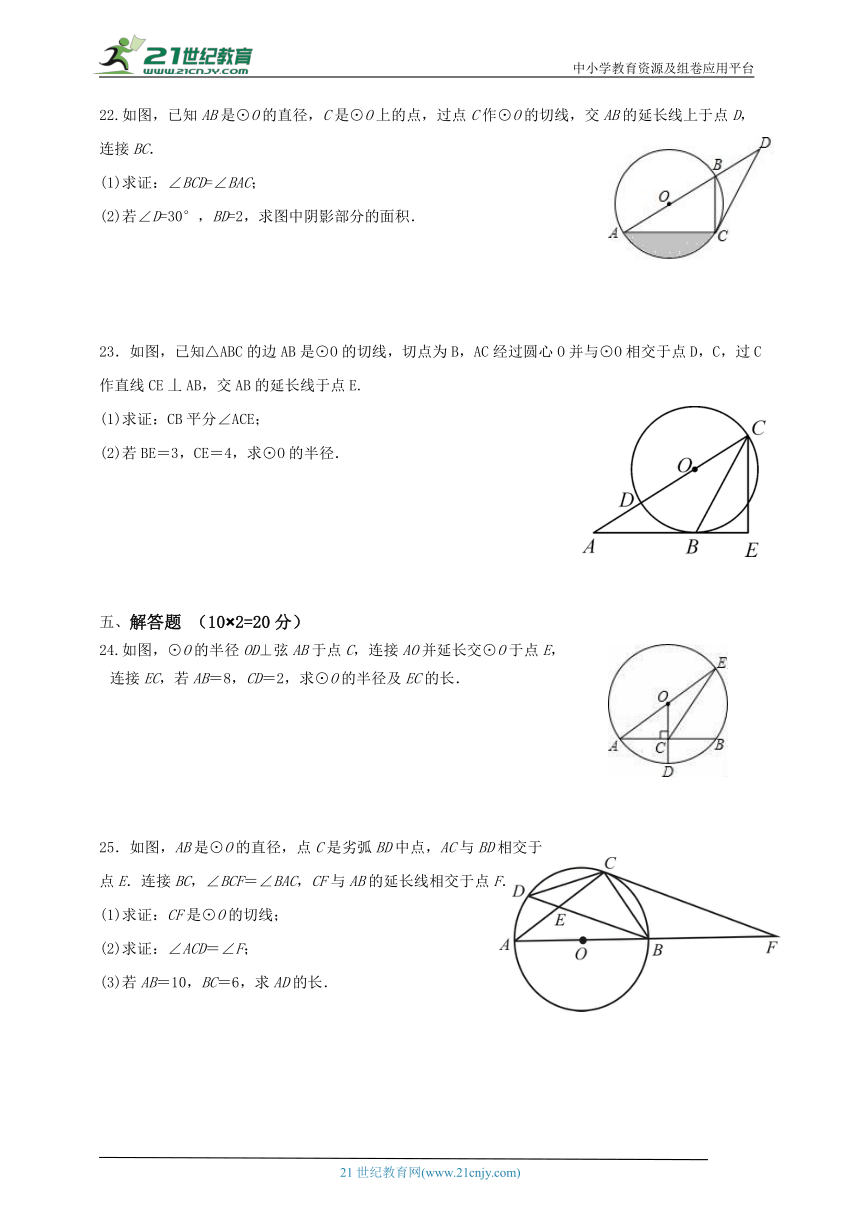
如图,已知A,B,C,D是⊙O上的点,若=,∠AOB=125°,
求∠COD的度数.
19.如图,在△OAB中OA=OB,⊙O交AB于点C、D,求证:AC=BD.
如图,已知在⊙O中,两条弦AB和CD交于点P,且AP=CP,
求证:AB=CD.
解答题(8×3=24分)
如图,残破的圆片上,弦AB的垂直平分线交弧AB于点C,交弦
AB于点D.
(1)求作此残片所在圆的圆心O(不写作法,保留作图痕迹);
(2)若AB=12 cm,⊙O的直径为20 cm,求CD的长.
22.如图,已知AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线,交AB的延长线上于点D,连接BC.
(1)求证:∠BCD=∠BAC;
(2)若∠D=30°,BD=2,求图中阴影部分的面积.
23.如图,已知△ABC的边AB是⊙O的切线,切点为B,AC经过圆心O并与⊙O相交于点D,C,过C作直线CE丄AB,交AB的延长线于点E.
(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
解答题 (10×2=20分)
24.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,
连接EC,若AB=8,CD=2,求⊙O的半径及EC的长.
如图,AB是⊙O的直径,点C是劣弧BD中点,AC与BD相交于
点E.连接BC,∠BCF=∠BAC,CF与AB的延长线相交于点F.
(1)求证:CF是⊙O的切线;
(2)求证:∠ACD=∠F;
(3)若AB=10,BC=6,求AD的长.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B C D D C B C C
二 、填空
题号 11 12 13 14 15 16 17
答案 60° 30 10 18
解答题
18.解:∵=,∴=,∴∠AOB=∠COD,
∵∠AOB=125°,
∴∠COD=125°.
19.证明:过点O作OE⊥AB于点E,
∵在⊙O中,OE⊥CD,
∴CE=DE,
∵OA=OB,OE⊥AB,
∴AE=BE,
∴AE﹣CE=BE﹣DE,
∴AC=BD.
20.证明:∵圆周角∠A和∠C都对着,
∴∠A=∠C,
在△ADP和△CBP中,
,
∴△ADP≌△CBP(ASA),
∴BP=DP,
∵AP=CP,
∴AP+BP=CP+DP,
即AB=CD.
21.解:(1)如图.
(2)如图,连接OB,
∵CD垂直平分AB,AB=12 cm,
∴BD=AD=AB=6 cm.
∵⊙O的直径为20 cm,
∴OB=OC=10 cm.
在Rt△OBD中,OB2=BD2+OD2,
即102=62+OD2,
∴OD==8(cm),
∴CD=OC-OD=10-8=2(cm).
22.(1)证明:如图,连接OC,
∵CD为⊙O的切线, ∴OC⊥CD,
∴∠BCD+∠OCB=90°,
∵AB是直径, ∴∠ACB=90°,
∴∠OCA+OCB =90°,∴∠OCA=∠BCD,
又∵OA=OC, ∴∠BAC=∠OCA,
∴∠BCD=∠BAC.
(2)解:设⊙O的半径为r, ∴AB=2r,
∵∠D=30°,∠OCD=90°,
∴OD=2OC=2r,∠COB=60°,
∵OD=OB+BD,∴r+2=2r, 解得r=2,
∴BC为斜边上的中线, ∴BC=OD =2,
又∵中,AB=2r=4,
由勾股定理可知,
∵OA=OB,
∴ ,
∵∠AOC=180°-∠COB=120°,
∴S扇形OAC=,
∴阴影部分面积为.
解:(1)证明:连接OB,∵AB是⊙O的切线,∴OB⊥AB.
∵CE丄AB,∴OB∥CE,∴∠OBC=∠BCE.
∵OB=OC,∴∠OBC=∠OCB.∴∠OCB=∠BCE,
∴CB平分∠ACE.
连接BD,在Rt△BCE中,
∵BE=3,CE=4,∴BC===5.
∵CD是⊙O的直径,∴∠DBC=90°,∴∠DBC=∠E,
又由(1)知∠BCD=∠BCE,∴△DBC∽△BEC,
∴=,∴CD===,
∴OC=CD=,
∴⊙O的半径为.
24.解:∵OD⊥弦AB,AB=8,
∴AC===4,
设⊙O的半径OA=r,
∴OC=OD﹣CD=r﹣2,
在Rt△OAC中,
r2=(r﹣2)2+42,
解得:r=5,
连接BE,如图,
∵OD=5,CD=2,
∴OC=3,
∵AE是直径,
∴∠ABE=90°,
∵OC是△ABE的中位线,
∴BE=2OC=6,
在Rt△CBE中,CE=.
25.(1)解:如图,连接OC
∵AB是直径∴∠ACB=90°
∴∠ACO+∠OCB=90°
∵OA=OC∴∠BAC=∠ACO
∵∠BCF=∠BAC ∴∠BCF +∠OCB=90°
∴∠OCF=90°∴OC⊥CF
∴CF是⊙O的切线
(2)∵点C是劣弧BD中点
∴∠CAD=∠BAC
∵∠BCF=∠BAC ∴∠CAD=∠BCF
∴∠CAD=∠CBD ∴∠BCF=∠CBD
∴CF∥BD ∴∠ABD=∠F
∴∠ACD=∠ABD
∴∠ACD=∠F
(3),
∴点H为BD的中点
∵AB=10,BC=6
设OH=x,则CH=5-x,根据勾股定理得
解得:
∵OH是中位线
∴
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
北师大版九年级数学下册《圆》测试卷B
满分:120分 考试时间:90分钟
选择题。(每小题3分,共30分)
1.下列说法中,正确的是( )
A.相等的圆心角所对的弧相等 B.过任意三点可以画一个圆
C.周长相等的圆是等圆 D.平分弦的直径垂直于弦
2.如图,CD为的直径,弦于点E,,,则直径CD的长是( )
A.4 B.8 C.26 D.10
第2题 第3题 第4题
3.如图在平面直角坐标系中,过格点A,B,C作一圆弧,圆心坐标是( )
A. B. C. D.
4.如图,在Rt△ABC中,∠ACB=90度.点P是半圆弧AC的中点,连接BP交AC于点D,若半圆弧的圆心为O,点D、点E关于圆心O对称.则图中的两个阴影部分的面积S1,S2之间的关系是( )
A.S1<S2 B.S1>S2 C.S1=S2 D.不确定
5.如图,AB是⊙O的直径,CD是⊙O的弦,CD⊥AB于点E,则下列结论不成立的是( )
A.∠A=∠D B.= C.∠ACB=90° D.∠COB=3∠D
`
(第5题) (第6题) (第7题)
6.如图,A,B,C是⊙O上的三个点,∠ABC=45°,连接AO,过点O作OE⊥BC交BC于点D,交⊙O于点E.若点D是OE的中点,则∠AOE的度数为( )
A.120° B.135° C.140° D.150°
7.如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A=25°,则∠D等于( )
A.20° B.30° C.40° D.50°
8.在圆柱形油槽内装有一些油,截面如图所示,直径MN为100cm,油面宽AB为60cm,如果再注入一些油后,油面宽变为80cm,则油面上升( )
A.70cm B.10cm或70cm C.10cm D.5cm或35cm
9.如图,弦CD与直径AB相交,连接BC、BD,若∠ABC=50°,则∠BDC=( )
A.20° B.30° C.40° D.50°
第8题 第9题 第10题
10.如图,AB是半圆O的直径,AC为弦,OD⊥AC于D,过点O作OE∥AC交半圆O于点E,过点E作EF⊥AB于F.若AC=2,则OF的长为( )
A. B. C.1 D.2
填空题(每小题4分共28分)
11.在⊙O中,弦AB的长恰好等于半径,弦AB所对的圆心角为 .
12.如图,OA、OB是⊙O的半径,C是⊙O上一点,∠AOB=40°,∠OBC=50°,则∠OAC= °.
第12题 第13题 第14题
13. 小华为了求出一个圆盘的半径,他用所学的知识,将一宽度为2 cm的刻度尺的一边与圆盘相切,另一边与圆盘边缘两个交点处的读数分别是“4”和“16”(单位:cm),如图所示,请你帮小华算出圆盘的半径是 cm.
14. 如图,将边长为3的正六边形铁丝框ABCDEF变形为以点A为圆心,AB为半径的扇形(忽略铁丝的粗细).则所得扇形AFB(阴影部分)的面积为 .
一圆锥的侧面展开图的圆心角为,底面半径为3,则该圆锥的侧面积为_______.
16.放置在直线l上的扇形AOB,先由位置①滚动(无滑动)到位置②,再由位置②滚动到位置③,如图所示.若半径OA=2,∠AOB=45°,则点O滚动的路径长为________.
17.如图,边长为2的正方形ABCD在等边长的正六边形外部做顺时针滚动,滚动一周回到初始位置时停止,点A在滚动过程中到出发点的最大距离是______.
第16题 第17题
解答题(6×3=18分)
如图,已知A,B,C,D是⊙O上的点,若=,∠AOB=125°,
求∠COD的度数.
19.如图,在△OAB中OA=OB,⊙O交AB于点C、D,求证:AC=BD.
如图,已知在⊙O中,两条弦AB和CD交于点P,且AP=CP,
求证:AB=CD.
解答题(8×3=24分)
如图,残破的圆片上,弦AB的垂直平分线交弧AB于点C,交弦
AB于点D.
(1)求作此残片所在圆的圆心O(不写作法,保留作图痕迹);
(2)若AB=12 cm,⊙O的直径为20 cm,求CD的长.
22.如图,已知AB是⊙O的直径,C是⊙O上的点,过点C作⊙O的切线,交AB的延长线上于点D,连接BC.
(1)求证:∠BCD=∠BAC;
(2)若∠D=30°,BD=2,求图中阴影部分的面积.
23.如图,已知△ABC的边AB是⊙O的切线,切点为B,AC经过圆心O并与⊙O相交于点D,C,过C作直线CE丄AB,交AB的延长线于点E.
(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
解答题 (10×2=20分)
24.如图,⊙O的半径OD⊥弦AB于点C,连接AO并延长交⊙O于点E,
连接EC,若AB=8,CD=2,求⊙O的半径及EC的长.
如图,AB是⊙O的直径,点C是劣弧BD中点,AC与BD相交于
点E.连接BC,∠BCF=∠BAC,CF与AB的延长线相交于点F.
(1)求证:CF是⊙O的切线;
(2)求证:∠ACD=∠F;
(3)若AB=10,BC=6,求AD的长.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 C D B C D D C B C C
二 、填空
题号 11 12 13 14 15 16 17
答案 60° 30 10 18
解答题
18.解:∵=,∴=,∴∠AOB=∠COD,
∵∠AOB=125°,
∴∠COD=125°.
19.证明:过点O作OE⊥AB于点E,
∵在⊙O中,OE⊥CD,
∴CE=DE,
∵OA=OB,OE⊥AB,
∴AE=BE,
∴AE﹣CE=BE﹣DE,
∴AC=BD.
20.证明:∵圆周角∠A和∠C都对着,
∴∠A=∠C,
在△ADP和△CBP中,
,
∴△ADP≌△CBP(ASA),
∴BP=DP,
∵AP=CP,
∴AP+BP=CP+DP,
即AB=CD.
21.解:(1)如图.
(2)如图,连接OB,
∵CD垂直平分AB,AB=12 cm,
∴BD=AD=AB=6 cm.
∵⊙O的直径为20 cm,
∴OB=OC=10 cm.
在Rt△OBD中,OB2=BD2+OD2,
即102=62+OD2,
∴OD==8(cm),
∴CD=OC-OD=10-8=2(cm).
22.(1)证明:如图,连接OC,
∵CD为⊙O的切线, ∴OC⊥CD,
∴∠BCD+∠OCB=90°,
∵AB是直径, ∴∠ACB=90°,
∴∠OCA+OCB =90°,∴∠OCA=∠BCD,
又∵OA=OC, ∴∠BAC=∠OCA,
∴∠BCD=∠BAC.
(2)解:设⊙O的半径为r, ∴AB=2r,
∵∠D=30°,∠OCD=90°,
∴OD=2OC=2r,∠COB=60°,
∵OD=OB+BD,∴r+2=2r, 解得r=2,
∴BC为斜边上的中线, ∴BC=OD =2,
又∵中,AB=2r=4,
由勾股定理可知,
∵OA=OB,
∴ ,
∵∠AOC=180°-∠COB=120°,
∴S扇形OAC=,
∴阴影部分面积为.
解:(1)证明:连接OB,∵AB是⊙O的切线,∴OB⊥AB.
∵CE丄AB,∴OB∥CE,∴∠OBC=∠BCE.
∵OB=OC,∴∠OBC=∠OCB.∴∠OCB=∠BCE,
∴CB平分∠ACE.
连接BD,在Rt△BCE中,
∵BE=3,CE=4,∴BC===5.
∵CD是⊙O的直径,∴∠DBC=90°,∴∠DBC=∠E,
又由(1)知∠BCD=∠BCE,∴△DBC∽△BEC,
∴=,∴CD===,
∴OC=CD=,
∴⊙O的半径为.
24.解:∵OD⊥弦AB,AB=8,
∴AC===4,
设⊙O的半径OA=r,
∴OC=OD﹣CD=r﹣2,
在Rt△OAC中,
r2=(r﹣2)2+42,
解得:r=5,
连接BE,如图,
∵OD=5,CD=2,
∴OC=3,
∵AE是直径,
∴∠ABE=90°,
∵OC是△ABE的中位线,
∴BE=2OC=6,
在Rt△CBE中,CE=.
25.(1)解:如图,连接OC
∵AB是直径∴∠ACB=90°
∴∠ACO+∠OCB=90°
∵OA=OC∴∠BAC=∠ACO
∵∠BCF=∠BAC ∴∠BCF +∠OCB=90°
∴∠OCF=90°∴OC⊥CF
∴CF是⊙O的切线
(2)∵点C是劣弧BD中点
∴∠CAD=∠BAC
∵∠BCF=∠BAC ∴∠CAD=∠BCF
∴∠CAD=∠CBD ∴∠BCF=∠CBD
∴CF∥BD ∴∠ABD=∠F
∴∠ACD=∠ABD
∴∠ACD=∠F
(3),
∴点H为BD的中点
∵AB=10,BC=6
设OH=x,则CH=5-x,根据勾股定理得
解得:
∵OH是中位线
∴
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
