四年级下册数学北师大版第二单元 认识三角形和四边形 整理与练习课件(共31张PPT)
文档属性
| 名称 | 四年级下册数学北师大版第二单元 认识三角形和四边形 整理与练习课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-01 10:32:58 | ||
图片预览





文档简介
(共31张PPT)
北师版四年级数学下册
认识三角形
和四边形
整理与练习
汇报人:XXX 时间:XXXXX
小组交流:本单元主要学习了哪些内容?
认识三角形和四边形
图形分类
三角形
立体图形
四边形
平面图形
三角形的分类
三角形的特征
平行四边形
梯形
四边形之间的关系
知识梳理
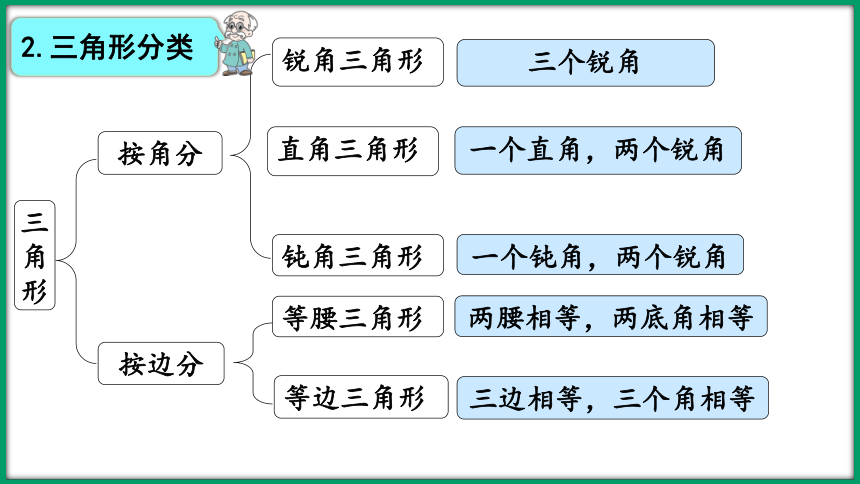
给图形分类时,不仅要弄清图形的类别特征,还 要了解图形之间的关系。部分学过的图形分类如下:
1.图形分类
三角形具有稳定性。
平行四边形易变形,不具有稳定性。
四边形和三角形的特征
按边分
按角分
锐角三角形
直角三角形
钝角三角形
三个锐角
一个直角,两个锐角
一个钝角,两个锐角
等腰三角形
等边三角形
两腰相等,两底角相等
三边相等,三个角相等
三角形
2.三角形分类
三角形的内角和
1.三角形内角和等于180°,与三角形的大小、形状无关。
2.根据三角形内角和等于180°,当已知三角形中两个内角的度数时,可以求出第三个内角的度数,并可以由此判断三角形的形状。
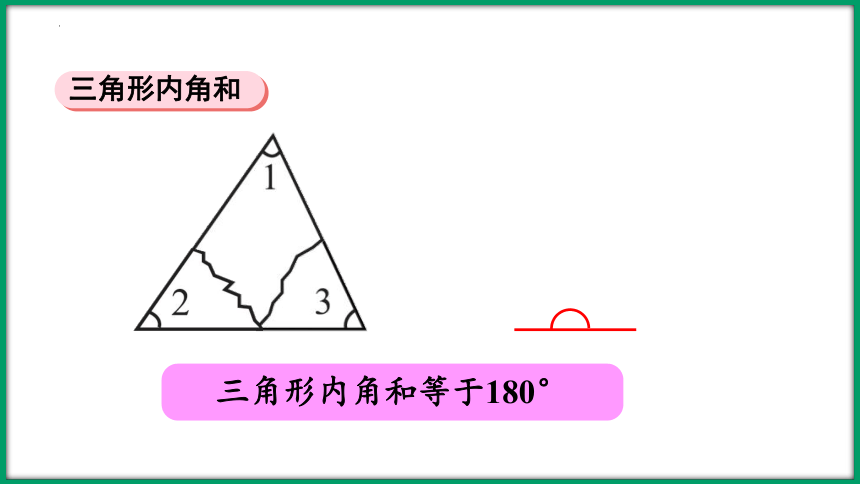
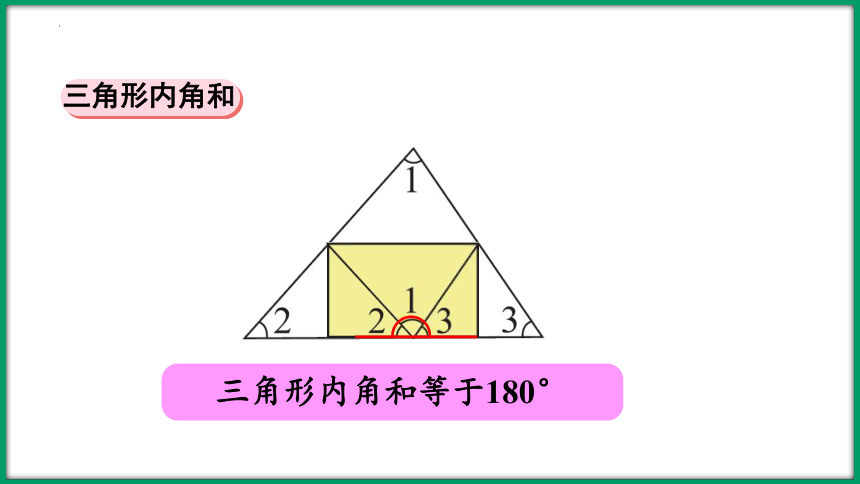
三角形内角和等于180°
三角形内角和
三角形内角和等于180°
三角形内角和
三角形边的关系
1. 三角形任意两边之和大于第三边。
2. 判断三条线段是否能围成三角形,只要把较短的两条线段的长度相加的和与第三条线段比较即可。若较短两边的长度和大于第三条线段,就一定能围成三角形;否则,就不能围成三角形。
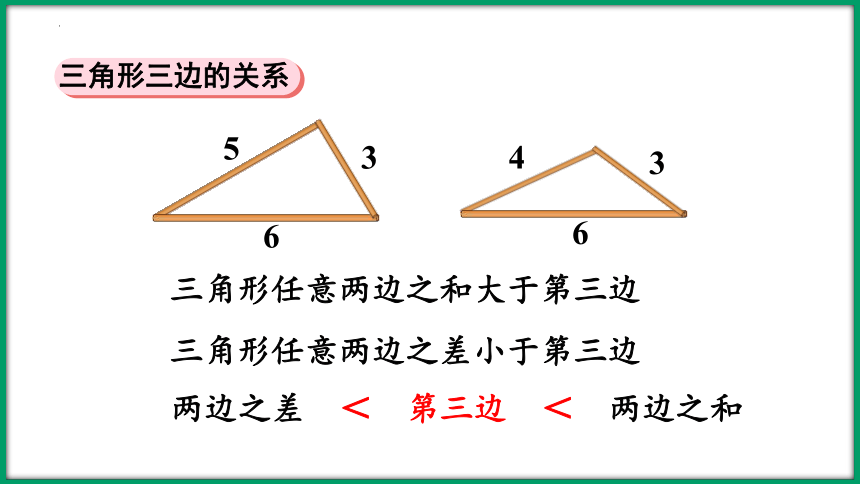
三角形任意两边之和大于第三边
三角形任意两边之差小于第三边
两边之差 < 第三边 < 两边之和
3
5
6
3
4
6
三角形三边的关系
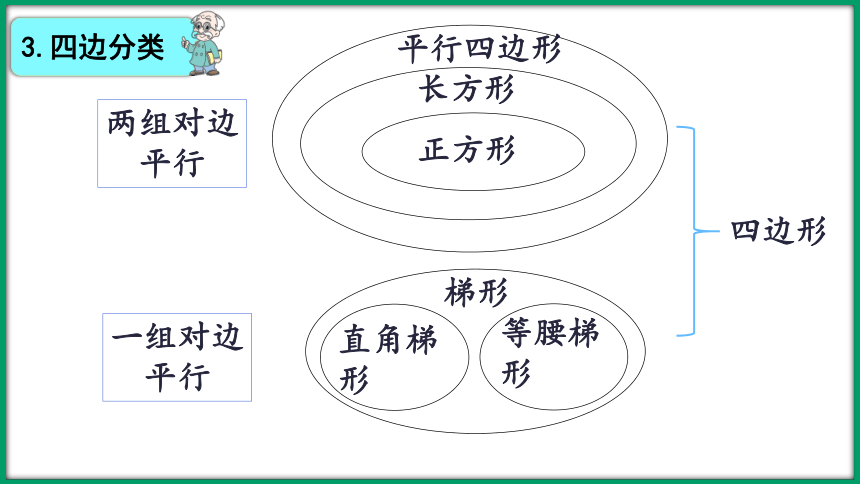
两组对边
平行
平行四边形
长方形
正方形
一组对边
平行
梯形
直角梯形
等腰梯形
四边形
3.四边分类
1.填空。
(1) 一个三角形既没有直角,也没有钝角,它是( 锐角 )
三角形。
解析:有一个角是直角的三角形是直角三角形,有一个角是钝角的三角形是钝角三角形,既没有直角又没有钝角,最大的角是锐角,就是锐角三角形。
锐角
课堂练习
(2)下图一共有( 5 )个三角形,其中有( 3 )个直角三角
形;有( 1 )个锐角三角形;有( 1 )个钝角三角形。
解析:注意数图形时要按角分类的方法逐个数,做到不重复、
不遗漏。
5
3
1
1
(3) 一个三角形的两个内角分别是72°和36°,第三个内角
是( 72 )°。它是一个( 锐角 )三角形,也是一个
( 等腰 )三角形。
72
锐角
等腰
解析:第三个内角是180°-72°-36°=72°,它的三个角都是锐角,所以它是一个锐角三角形,又因为两个内角都是72°,所以它也是一个等腰三角形。
(4) 在一个直角三角形中,一个锐角是30°,另一个锐角是
( 60 )°;三边相等的三角形中,每个角都是
( 60 )°。
解析:根据题意可得,直角三角形的两个锐角的和是90°,所以另一个锐角是90°-30°=60°;三边相等的三角形是等边三角形,在等边三角形中,三个内角的度数都相等,所以每个内角的度数是180°÷3=60°。
60
60
(5) 一个等腰三角形的顶角是80°,则它的底角是
( 50 )°;若底角是80°,则它的顶角是( 20 )°。
50
20
解析:等腰三角形的两个底角度数相等,当顶角是80°时,用三角形内角和减去顶角的度数再除以2即可求出一个底角的度数,即(180°-80°)÷2=50°;当底角是80°时,用三角形内角和减去两个底角的度数即可求得顶角的度数,即180°-80°×2=20°。
(6) 用三根小棒围成一个三角形,如果其中的两根小棒是7
厘米和10厘米,则第三根小棒最长是( 16 )厘米,最短
是( 4 )厘米。(填整厘米数)
16
4
解析:根据三角形任意两边之和大于第三边,可知7厘米+10厘米>第三条边的长度,即第三条边的长度一定小于17厘米,而第三条边也可以是较短的,则第三条边的长度+7 厘米>10 厘米,即第三条边的长度要大于3厘米,所以第三条边的长度在3厘米与17厘米之间(不包括3厘米和17厘米),所以第三条边最短是4厘米,最长是16厘米。
(7) 三根同样长的木棒首尾相连拼成了一个三角形,这个三
角形的周长是126厘米。每根木棒长( 42 )厘米,围成
的三角形各角的度数分别是( 60 )°、( 60 )°、
( 60 )°。
解析:已知三角形的周长,且三根木棒同样长,则每根木棒长
126÷3=42(厘米)。由三根木棒同样长可知,这是一个等边三角
形,所以每个角的度数是60°。
42
60
60
60
(8)只有一组对边平行,但另一组对边相等的四边形,它是
( 等腰梯 )形。
解析:只有一组对边平行的四边形是梯形,两腰相等的梯形是等腰梯形,据此解答。
等腰梯
(9) 有直角、两组对边分别平行且邻边相等的四边形,它是
( 正方 )形。
解析:两组对边分别平行的四边形是平行四边形,有直角且邻边相等的平行四边形是正方形。
正方
(10) ( 长方形 )和( 正方形 )都是特殊的平行四边形;
正方形还满足( 邻边 )相等,故正方形是特殊的
( 长方形 )。
解析:两组对边分别平行的四边形是平行四边形,长方形和正方形都是两组对边分别平行的四边形,正方形的四条边相等,所以正方形的邻边相等,因此正方形是特殊的长方形。
长方形
正方形
邻边
长方形
2.计算下面图中各角的度数
(1) (2)
∠1=( 105° ) ∠2=( 70° )
解析:∠1=180°-45°-30°=105°。
解析:∠2=180°-65°-45°=70°。
105°
70°
(3)
∠1=( 30° ) ∠2=( 60° )
解析:∠1和60°组成一个直角,所以∠1=90°-60°=30°;
∠1和∠2所在的三角形是直角三角形,所以∠2=180°-90°-
∠1=180°-90°-30°=60°。
30°
60°
(4) 用两种方法求∠1的度数。
方法一:180°-60°=120°
∠1=180°-120°-25°=35°
方法二:180°-45°-60°=75°
180°-45°-25°=110°
∠1=110°-75°=35°
解析:方法一:如图所示: ,∠2和60°的角组成平角,
可得∠2=180°-60°=120°,由∠2+25°+∠1=180°,可得
∠1=∠180°-120°-25°=35°;方法二:如图所
示: ,根据45°+60°+∠2=180°可求出∠2=180°
-45°-60°=75°,由45°+25°+∠1+∠2=180°,可求出
∠2+∠1=180°-45°-25°=110°,则∠1=110°-∠2=
110°-75°=35°。
3. 典典说得对吗?请说明理由。
典典说得不对。典典的两条腿和地面可以组成一个等腰三
角形,他的腿长是80 cm,80+80=160(cm),根据三角
形任意两边之和大于第三边的特性可知,160 cm应大于
典典一步的长度,即典典走一步的长度<160 cm<2 m,
所以典典说得不对。
解析:根据三角形任意两边之和大于第三边解答。
4 一根铁丝可以围成一个腰长12厘米,底边长18厘米的等
腰三角形。如果改围成一个等边三角形,那么等边三角
形的边长是多少厘米?(7分)
(12+12+18)÷3=14(厘米)
答:等边三角形的边长是14厘米。
解析:等腰三角形两条腰长相等,一个腰长是12厘米,则另一个腰
长也是12厘米,所以它的周长是(12+12+18)厘米,再根据等边三
角形三条边相等,用周长÷3即可解答。
5. 爷爷用篱笆围了一个边长为8 dm的正方形,现在把它拆
开围成一个底边长是10 dm的等腰三角形,这个等腰三角
形的腰长是多少?(7分)
(8×4-10)÷2=11(dm)
答:这个等腰三角形的腰长是11 dm。
解析:等腰三角形的腰长相等,等腰三角形的一条腰长=(周长-底边长)÷2。由题可知等腰三角形和正方形的周长相等,正方形的周长=边长×4,据此解答。
6.一根铁丝可以围成一个有两条边的长分别是12 cm和24
cm的等腰三角形,若用这根铁丝围成一个长是宽的2倍
的长方形,围成的长方形的面积是多少平方厘米?(7分)
12+24+24=60(cm)
宽:60÷2÷(1+2)=10(cm)
长:10×2=20(cm)
面积:20×10=200(cm2)
答:围成的长方形的面积是200 cm2。
解析:若腰长是12 cm,12+12=24(cm),根据三角形三边关系可
知,不能围成三角形。若腰长是24 cm,12 cm+24 cm>24 cm,
能围成三角形,所以它的周长是12+24+24=60(cm)。因为是同一
根铁丝围的等腰三角形和长方形,所以等腰三角形的周长等于长方
形的周长。把长方形的宽看作1份,那么长就是2份,根据长方形的
周长=(长+宽)×2,可以求出1份的长度,即长方形的宽是
60÷2÷(1+2)=10(cm),长为10×2=20(cm),再根据长方形的面
积=长×宽,可得长方形的面积=20×10=200(cm2)。
1. 在折纸活动中,龙龙把一张长方形纸的一角向上折叠,
已知∠1=30°,请你算一算∠2的度数是多少。(9分)
90°-30°×2=30°
∠2=180°-30°-90°=60°
答:∠2的度数是60°。
解析:长方形折起后,∠1=30°,故∠ABC被均分成三等份。
思维拓展
2.用小棒照样子摆一摆。
如图,摆1个梯形要4根小棒,摆2个梯形要7根小棒,摆3
个梯形要10根小棒,摆6个梯形要( 19 )根小棒,37根
小棒可以摆( 12 )个梯形。
19
12
解析:根据小棒摆的规律可知,后面每增加一个梯形就多出3根小棒,由此得出摆n个梯形需要4+3×(n-1)=3n+1(根)小棒,当n=6时,需要3×6+1=19(根)小棒,即小棒总根数=梯形个数×3+1,当有37根小棒时,可以摆(37-1)÷3=12(个)梯形。
北师版四年级数学下册
认识三角形
和四边形
整理与练习
汇报人:XXX 时间:XXXXX
小组交流:本单元主要学习了哪些内容?
认识三角形和四边形
图形分类
三角形
立体图形
四边形
平面图形
三角形的分类
三角形的特征
平行四边形
梯形
四边形之间的关系
知识梳理
给图形分类时,不仅要弄清图形的类别特征,还 要了解图形之间的关系。部分学过的图形分类如下:
1.图形分类
三角形具有稳定性。
平行四边形易变形,不具有稳定性。
四边形和三角形的特征
按边分
按角分
锐角三角形
直角三角形
钝角三角形
三个锐角
一个直角,两个锐角
一个钝角,两个锐角
等腰三角形
等边三角形
两腰相等,两底角相等
三边相等,三个角相等
三角形
2.三角形分类
三角形的内角和
1.三角形内角和等于180°,与三角形的大小、形状无关。
2.根据三角形内角和等于180°,当已知三角形中两个内角的度数时,可以求出第三个内角的度数,并可以由此判断三角形的形状。
三角形内角和等于180°
三角形内角和
三角形内角和等于180°
三角形内角和
三角形边的关系
1. 三角形任意两边之和大于第三边。
2. 判断三条线段是否能围成三角形,只要把较短的两条线段的长度相加的和与第三条线段比较即可。若较短两边的长度和大于第三条线段,就一定能围成三角形;否则,就不能围成三角形。
三角形任意两边之和大于第三边
三角形任意两边之差小于第三边
两边之差 < 第三边 < 两边之和
3
5
6
3
4
6
三角形三边的关系
两组对边
平行
平行四边形
长方形
正方形
一组对边
平行
梯形
直角梯形
等腰梯形
四边形
3.四边分类
1.填空。
(1) 一个三角形既没有直角,也没有钝角,它是( 锐角 )
三角形。
解析:有一个角是直角的三角形是直角三角形,有一个角是钝角的三角形是钝角三角形,既没有直角又没有钝角,最大的角是锐角,就是锐角三角形。
锐角
课堂练习
(2)下图一共有( 5 )个三角形,其中有( 3 )个直角三角
形;有( 1 )个锐角三角形;有( 1 )个钝角三角形。
解析:注意数图形时要按角分类的方法逐个数,做到不重复、
不遗漏。
5
3
1
1
(3) 一个三角形的两个内角分别是72°和36°,第三个内角
是( 72 )°。它是一个( 锐角 )三角形,也是一个
( 等腰 )三角形。
72
锐角
等腰
解析:第三个内角是180°-72°-36°=72°,它的三个角都是锐角,所以它是一个锐角三角形,又因为两个内角都是72°,所以它也是一个等腰三角形。
(4) 在一个直角三角形中,一个锐角是30°,另一个锐角是
( 60 )°;三边相等的三角形中,每个角都是
( 60 )°。
解析:根据题意可得,直角三角形的两个锐角的和是90°,所以另一个锐角是90°-30°=60°;三边相等的三角形是等边三角形,在等边三角形中,三个内角的度数都相等,所以每个内角的度数是180°÷3=60°。
60
60
(5) 一个等腰三角形的顶角是80°,则它的底角是
( 50 )°;若底角是80°,则它的顶角是( 20 )°。
50
20
解析:等腰三角形的两个底角度数相等,当顶角是80°时,用三角形内角和减去顶角的度数再除以2即可求出一个底角的度数,即(180°-80°)÷2=50°;当底角是80°时,用三角形内角和减去两个底角的度数即可求得顶角的度数,即180°-80°×2=20°。
(6) 用三根小棒围成一个三角形,如果其中的两根小棒是7
厘米和10厘米,则第三根小棒最长是( 16 )厘米,最短
是( 4 )厘米。(填整厘米数)
16
4
解析:根据三角形任意两边之和大于第三边,可知7厘米+10厘米>第三条边的长度,即第三条边的长度一定小于17厘米,而第三条边也可以是较短的,则第三条边的长度+7 厘米>10 厘米,即第三条边的长度要大于3厘米,所以第三条边的长度在3厘米与17厘米之间(不包括3厘米和17厘米),所以第三条边最短是4厘米,最长是16厘米。
(7) 三根同样长的木棒首尾相连拼成了一个三角形,这个三
角形的周长是126厘米。每根木棒长( 42 )厘米,围成
的三角形各角的度数分别是( 60 )°、( 60 )°、
( 60 )°。
解析:已知三角形的周长,且三根木棒同样长,则每根木棒长
126÷3=42(厘米)。由三根木棒同样长可知,这是一个等边三角
形,所以每个角的度数是60°。
42
60
60
60
(8)只有一组对边平行,但另一组对边相等的四边形,它是
( 等腰梯 )形。
解析:只有一组对边平行的四边形是梯形,两腰相等的梯形是等腰梯形,据此解答。
等腰梯
(9) 有直角、两组对边分别平行且邻边相等的四边形,它是
( 正方 )形。
解析:两组对边分别平行的四边形是平行四边形,有直角且邻边相等的平行四边形是正方形。
正方
(10) ( 长方形 )和( 正方形 )都是特殊的平行四边形;
正方形还满足( 邻边 )相等,故正方形是特殊的
( 长方形 )。
解析:两组对边分别平行的四边形是平行四边形,长方形和正方形都是两组对边分别平行的四边形,正方形的四条边相等,所以正方形的邻边相等,因此正方形是特殊的长方形。
长方形
正方形
邻边
长方形
2.计算下面图中各角的度数
(1) (2)
∠1=( 105° ) ∠2=( 70° )
解析:∠1=180°-45°-30°=105°。
解析:∠2=180°-65°-45°=70°。
105°
70°
(3)
∠1=( 30° ) ∠2=( 60° )
解析:∠1和60°组成一个直角,所以∠1=90°-60°=30°;
∠1和∠2所在的三角形是直角三角形,所以∠2=180°-90°-
∠1=180°-90°-30°=60°。
30°
60°
(4) 用两种方法求∠1的度数。
方法一:180°-60°=120°
∠1=180°-120°-25°=35°
方法二:180°-45°-60°=75°
180°-45°-25°=110°
∠1=110°-75°=35°
解析:方法一:如图所示: ,∠2和60°的角组成平角,
可得∠2=180°-60°=120°,由∠2+25°+∠1=180°,可得
∠1=∠180°-120°-25°=35°;方法二:如图所
示: ,根据45°+60°+∠2=180°可求出∠2=180°
-45°-60°=75°,由45°+25°+∠1+∠2=180°,可求出
∠2+∠1=180°-45°-25°=110°,则∠1=110°-∠2=
110°-75°=35°。
3. 典典说得对吗?请说明理由。
典典说得不对。典典的两条腿和地面可以组成一个等腰三
角形,他的腿长是80 cm,80+80=160(cm),根据三角
形任意两边之和大于第三边的特性可知,160 cm应大于
典典一步的长度,即典典走一步的长度<160 cm<2 m,
所以典典说得不对。
解析:根据三角形任意两边之和大于第三边解答。
4 一根铁丝可以围成一个腰长12厘米,底边长18厘米的等
腰三角形。如果改围成一个等边三角形,那么等边三角
形的边长是多少厘米?(7分)
(12+12+18)÷3=14(厘米)
答:等边三角形的边长是14厘米。
解析:等腰三角形两条腰长相等,一个腰长是12厘米,则另一个腰
长也是12厘米,所以它的周长是(12+12+18)厘米,再根据等边三
角形三条边相等,用周长÷3即可解答。
5. 爷爷用篱笆围了一个边长为8 dm的正方形,现在把它拆
开围成一个底边长是10 dm的等腰三角形,这个等腰三角
形的腰长是多少?(7分)
(8×4-10)÷2=11(dm)
答:这个等腰三角形的腰长是11 dm。
解析:等腰三角形的腰长相等,等腰三角形的一条腰长=(周长-底边长)÷2。由题可知等腰三角形和正方形的周长相等,正方形的周长=边长×4,据此解答。
6.一根铁丝可以围成一个有两条边的长分别是12 cm和24
cm的等腰三角形,若用这根铁丝围成一个长是宽的2倍
的长方形,围成的长方形的面积是多少平方厘米?(7分)
12+24+24=60(cm)
宽:60÷2÷(1+2)=10(cm)
长:10×2=20(cm)
面积:20×10=200(cm2)
答:围成的长方形的面积是200 cm2。
解析:若腰长是12 cm,12+12=24(cm),根据三角形三边关系可
知,不能围成三角形。若腰长是24 cm,12 cm+24 cm>24 cm,
能围成三角形,所以它的周长是12+24+24=60(cm)。因为是同一
根铁丝围的等腰三角形和长方形,所以等腰三角形的周长等于长方
形的周长。把长方形的宽看作1份,那么长就是2份,根据长方形的
周长=(长+宽)×2,可以求出1份的长度,即长方形的宽是
60÷2÷(1+2)=10(cm),长为10×2=20(cm),再根据长方形的面
积=长×宽,可得长方形的面积=20×10=200(cm2)。
1. 在折纸活动中,龙龙把一张长方形纸的一角向上折叠,
已知∠1=30°,请你算一算∠2的度数是多少。(9分)
90°-30°×2=30°
∠2=180°-30°-90°=60°
答:∠2的度数是60°。
解析:长方形折起后,∠1=30°,故∠ABC被均分成三等份。
思维拓展
2.用小棒照样子摆一摆。
如图,摆1个梯形要4根小棒,摆2个梯形要7根小棒,摆3
个梯形要10根小棒,摆6个梯形要( 19 )根小棒,37根
小棒可以摆( 12 )个梯形。
19
12
解析:根据小棒摆的规律可知,后面每增加一个梯形就多出3根小棒,由此得出摆n个梯形需要4+3×(n-1)=3n+1(根)小棒,当n=6时,需要3×6+1=19(根)小棒,即小棒总根数=梯形个数×3+1,当有37根小棒时,可以摆(37-1)÷3=12(个)梯形。
