四年级下册数学北师大版第五单元认识方程 整理与复习(1)(课件)(共43张PPT)
文档属性
| 名称 | 四年级下册数学北师大版第五单元认识方程 整理与复习(1)(课件)(共43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-07 15:07:56 | ||
图片预览








文档简介
(共43张PPT)
北师版四年级数学下册
认识方程
整理与复习(1)
汇报人:XXX 时间:XXXXX
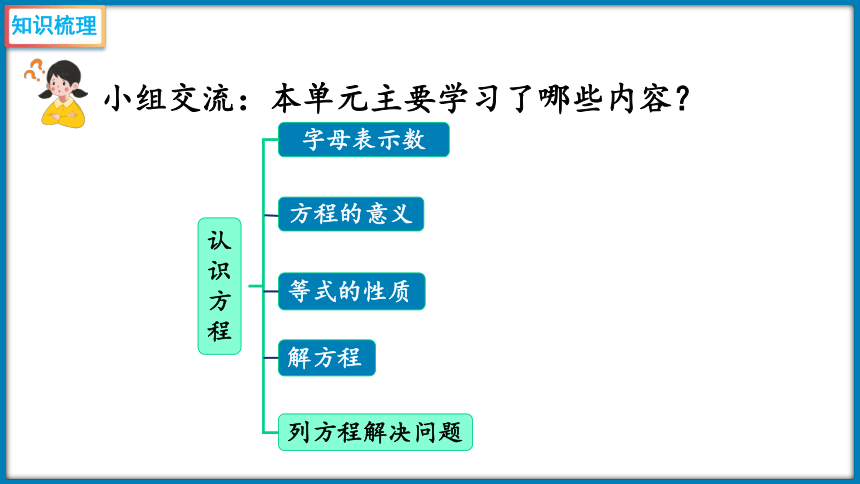
小组交流:本单元主要学习了哪些内容?
认识方程
字母表示数
方程的意义
列方程解决问题
等式的性质
解方程
知识梳理
02
03
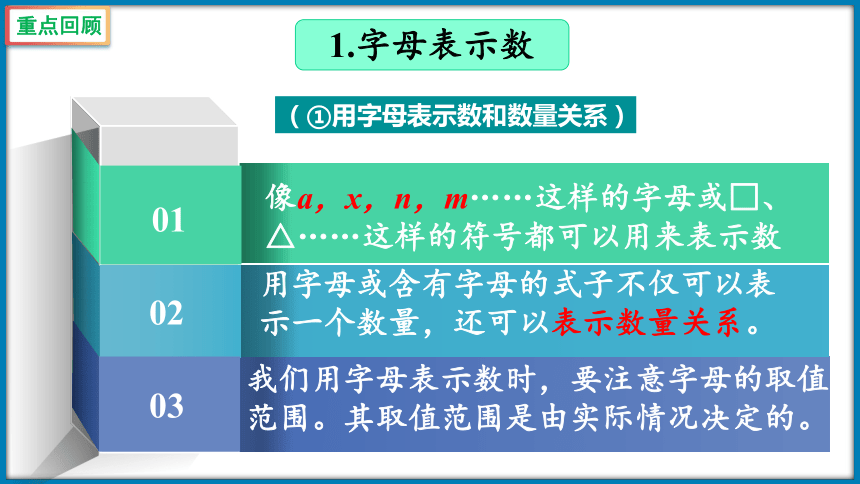
我们用字母表示数时,要注意字母的取值范围。其取值范围是由实际情况决定的。
01
像a,x,n,m……这样的字母或□、△……这样的符号都可以用来表示数
用字母或含有字母的式子不仅可以表示一个数量,还可以表示数量关系。
重点回顾
1.字母表示数
(①用字母表示数和数量关系)
1. 填一填。
(1)公共汽车上原来有x人,在青少年宫站有5人上车,又有6人下车,现在车上有乘客( )人。
(2)一本故事书98页,平均每天看x页,看了6天,还剩( )页。一本《数学竞赛》a元,买5本要( )元。
(3)一个两位数,十位上的数字是a,个位上的数字是b,那么这个两位数用( )表示。
x+5-6
98-6x
5a
10a+b
+5
-6
6x
a个10
b个1
用字母不仅可以表示一个数,还可以表示几个数量之间的关系。
2.你能说出下面含有字母的式子所表示的意思吗?
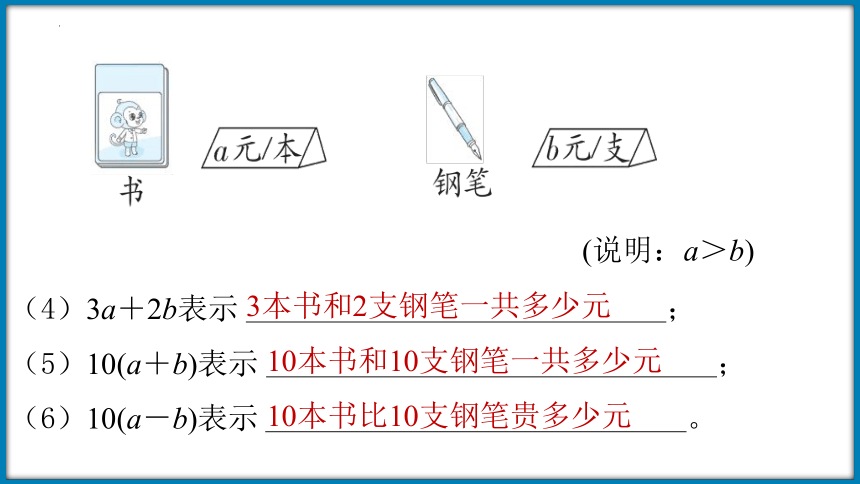
a元/块 b元/盒
(1)2a+b表示
(2)3b表示
(3)2(a-b)表示
2块面包和1盒牛奶的总价。
3盒牛奶的总价。
2块面包比2盒牛奶多多少元。
(答案不唯一)
(说明:a>b)
(4)3a+2b表示 ;
(5)10(a+b)表示 ;
(6)10(a-b)表示 。
3本书和2支钢笔一共多少元
10本书和10支钢笔一共多少元
10本书比10支钢笔贵多少元
02
03
用字母表示计算公式和运算定律比文字叙述更简明易记、便于应用。
01
在含有字母的式子里,数字和字母中间的乘号可以记作“·” ,也可以省略不写,但数字必须写在字母的前边。
a 读作a的平方,表示两个a 相乘,2a表示两个a相加。
1.字母表示数
②(用字母表示公式和运算律)
重点回顾
3. 省略乘号并化简下列各式。
3×x = m×52 = n×8 = x×y×z =
7×y+8×y = 2a+3a+6 =
12×x-7×x = 2.5×c-c =
3x
52m
8n
xyz
15y
5a+6
5x
1.5c
在用字母表示的式子里,乘号可以用“·”代替,或省略不写;利用乘法的分配律还可以对一些较复杂的式子进行化简。
4. 填一填,说一说。
用字母可以表示我们学过的运算律、运算性质、计算公式以及常用的数量关系。
(15.5+x)+9=15.5+( + )
7.5×a+2.5×a=a×( )
35-x-y=35 -( + )
s=v×( )
S平行四边形=a×( )
9
7.5+2.5
x
y
t
加法结合律
乘法分配律
x
连减的性质
速度、时间和路程的关系
h
平行四边形面积公式
运算律 用字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
α+b+c=α+(b+c)
α×b=b×α
(α×b)×c=α×(b×c)
(α+b)×c=α×c+b×c
α+b=b+α
α·b=b·α或αb=bα
(α·b)·c=α·(b·c)或(αb)c=α(bc)
(α+b)·c=α·c+b·c或(α+b)c=αc+bc
用字母表示运算定律,简明易记、便于应用。
运算律 用语言描述
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
两个数相加,交换加数的位置,和不变。
三个数相加,先把前两个数相加,或者先
把后两个数相加,结果不变。
两个数相乘,交换因数的位置,积不变。
三个数相乘,先把前两个数相乘,或者先
把后两个数相乘,结果不变。
两个数的和同一个数相乘,可以先把这两个加数
分别同这个数相乘,再把两个积相加,结果不变。
运算律 用字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
α+b+c=α+(b+c)
α+b=b+α
α·b=b·α或αb=bα
(α·b)·c=α·(b·c)或(αb)c=α(bc)
(α+b)·c=α·c+b·c或(α+b)c=αc+bc
02
03
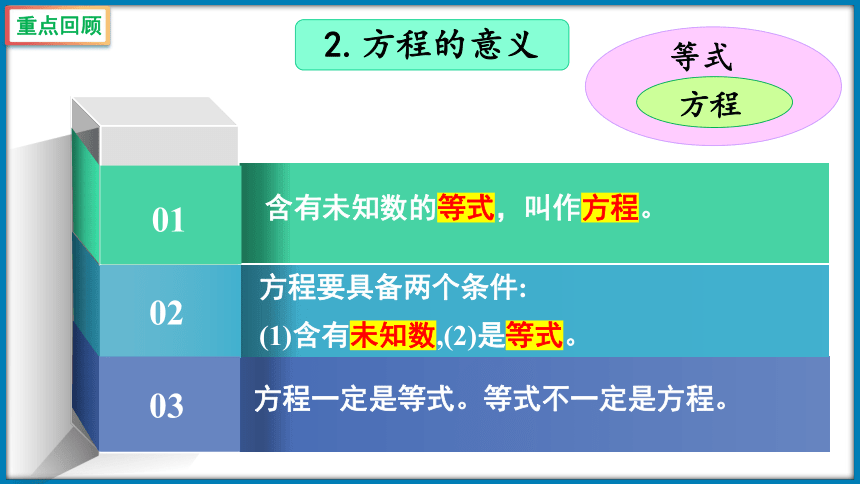
方程一定是等式。等式不一定是方程。
01
含有未知数的等式,叫作方程。
方程要具备两个条件:
(1)含有未知数,(2)是等式。
重点回顾
2.方程的意义
等式
方程
这些等式有什么特点?与同伴进行交流。
2000=2z+200
4y=2000
10=x+2
用等号将相等的量连接起来,表示相等关系的
式子就是等式。
等式
像200+2z=2000,4y=2000 10=x+2 这样,根据等量关系列出的含有未知数的等式就是方程。
等式
未知数
不等式
x+ 20 <100
x + 20 > 50
10 < 100
等式
不含未知数
100+100=200
x + 20 = 70
方程
2 x = 150
3 x + 10 = 100
x + 10 = 15
分类整理
含有未知数
5.选一选。
下列式子中,等式有( C )个,方程有( B )个。
①2x+8 ②a+1.5=7 ③48+16=64
④6x+7=25
C
B
⑤2y-1.8>4.2 ⑥6a2=24
A.2 B.3 C.4
解析:含有等号的式子就是等式,②③④⑥是等式;含有未知数的等式才是方程,②④⑥是方程。
6.看图列方程。
(1)
70+x=100
(2)
3x+100=220
3a+156=208
解析:由图可知,3个a米加上156米等于208米,据此列出方程。
(3)
02
01
等式两边加上或减去同一个数,左右两边仍然相等。
等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
重点回顾
3.等式的性质
7.想一想,填一填,你发现了什么?
(1) 因为60-20=40,所以60-20+20=40+( 20 )。
(2) 因为x+2.4=10,所以x+2.4-2.4=10-( 2.4 )。
我发现:等式两边都加上(或减去)( 同一个 ),等式仍然成立。
20
2.4
同一个数
(3)在 里填上适当的运算符号,在 内填上适当的数,使天
平平衡。
+
10
20.5
-
8.在 里填上运算符号,在 里填上合适的数。
(1) 4x=12 4x÷4=12 ÷ 4
(2) x÷7=15 x÷7×7=15 × 7
我发现:等式两边都( 乘 )同一个数或( 除以 )同一个不为0的数,等式仍然成立。
÷
4
×
7
乘
除以
02
03
解方程的格式:先写解,点上冒号,等号对齐。
01
使方程左右两边相等的未知数的值,叫做方程的解;
求方程的解的过程叫做解方程;
重点回顾
4.解方程
23+x = 45
解: 23+x-23
=
45-23
x
=
22
“方程的解”中的“解”字是名词,表示一个具体的数;
“解方程”中的“解”字是动词,指求出方程的解的过程。
使方程左右两边相等的未知数的值,叫做方程的解。
求方程解的过程叫做解方程。
解方程的一般步骤
① 先写“解:”
②根据等式的性质使等式两边发生变化,使左边只含有未知数
③ 求出未知数的值
④ 检验
解方程。
-7=12
解:
-7+7=12+7
=19
第二行起
写“解”
等号对齐
x=19是不是正确的答案呢?检验一下。
方程左边=y-7
=19-7
=12
=方程右边
所以,x=19是方程的解。
检验时,如果方程左边不等于右边,
就说明这个值不是方程的解。
19-7=12, =19对了。
1.形如x±ɑ=b的方程的解法
x+a=b x-a=b
解: x+a-a=b-a 解:x-a+a=b+a
x=b-a x=b+a
a-x=b
解:a-x+x=b+x
a=b+x
x+b=a
x+b-b=a-b
x=a-b
ɑx=b x÷a =b
解:ax÷a =b÷ɑ 解:x÷a×a =b×ɑ
x =b÷ɑ x =b×ɑ
a÷x=b
解:a÷x×x=b×x
a=b×x
b×x=a
b×x÷b=a÷b
x=a÷b
2.形如ɑx=b和x÷a =b的方程的解法
9. 解方程并检验。
(1)18+x=32
解: 18+x-18=32-18
x=14
方程左边 =18+x
=18+14
=32
=方程右边
所以,x=14是方程的解。
检验
(2)x-13.4=6.8
解: x-13.4+13.4=6.8+13.4
x=20.2
方程左边 =x-13.4
=20.2 -13.4
=6.8
=方程右边
所以,x=20.2是方程的解。
检验
x=11
解:20-x+x=9+x
20=9+x
9+x=20
9+x-9=20-9
(3)20-x = 9。
方程左边=20-x
= 20-11
=9
=方程右边
所以,x=11是方程的解。
检验
交流小结:解方程需要注意什么?
1.解方程的依据是等式的性质1,解答时要注意格式,
还要记得检验。
2.加法、最简单:
加几就减去几。
3.减法、要注意:
x在前,很简单。减去几就加几。
x在后,挺麻烦。先消x后消数,中间还需调个头。
(4)5x=1.5
解:5x÷5=1.5÷5
x=0.3
方程左边=5x
=5×0.3
=1.5
=方程右边
所以,x=0.3是方程的解。
检验
解:x÷1.1×1.1=3×1.1
x=3.3
(5)x÷1.1=3
方程左边=x÷1.1
=3.3÷1.1
=3
=方程右边
所以,x=3.3是方程的解。
检验
x=7
解:21÷x×x=3×x
21=3×x
3×x=2.1
3x÷3=21÷3
(6)21÷x = 3
方程左边=21÷x
= 21÷7
=3
=方程右边
所以,x =7是方程的解。
检验
交流小结:解方程需要注意什么?
1.解方程的依据是等式的性质2,解答时要注意格式,
还要记得检验。
2.乘法最简单:
乘几就除以几。
3.除法要注意:
x在前,很简单。;除以几就乘几。
x在后,挺麻烦。先消x后消数,中间还需调个头。
老师告诉你:
解稍复杂的方程,一般运用等式的性质。但当未知数
是减数或除数时,运用减法或除法各部分之间的关系去解
相对简单。对于有些稍复杂的方程,还要先运用乘法分配
律将方程中的式子展开,再运用等式的性质去解。另外,
要判断所解方程是否正确,解方程后还要进行检验。
拓展延伸
解方程:3(x-15)-15=2x-10
例
思路分析:这个方程的左边有括号,先运用乘法分配律将左边展开得3x-45-15,再合并得3x-60,原方程就变成了3x-60=2x-10,最后运用等式的性质去解。等式两边都是减法,要先看减得多的,因此,等式两边同时加上60,方程变成3x=2x+50,再将等式两边同时减去2x,即得方程的解为x=50。
规范解答: 3(x-15)-15=2x-10
解:3x-45-15=2x-10
3x-60=2x-10
3x=2x+50
x=50
技巧1
运用各部分的关系解方程
1.解方程。
54-3x=24
解:3x=30
x=10
78-4x=22
解:4x=56
x=14
96÷(2x)=12
解:2x=8
x=4
120÷(4x)=5
解:4x=24
x=6
技巧2
运用等式的性质解方程
2.解方程。
3x+1.2×5=48
解: 3x+6=48
3x=42
x=14
8x-27÷3=15
解:8x-9=15
8x=24
x=3
8x-3=7x+3
解:8x-7x=3+3
x=6
5x+24=4x×2
解: 5x+24=8x
8x-5x=24
3x=24
x=8
解:2x=12
x=6
12-6x=8-2x
解:4x=4
x=1
6x-8=4x+4
技巧3
运用乘法分配律解方程
3.解方程。
8(18-x)-5x=53
解:144-8x-5x=53
144-13x=53
13x=91
x=7
4(x-2)=3(x+3)
解: 4x-8=3x+9
4x-3x=9+8
x=17
2(x-13)=(x+8×2)+13
解: 2x-26=x+16+13
2x-26=x+29
x=55
3(x-8)-6=2(x-8)
解: 3x-24-6=2x-16
3x-30=2x-16
x=14
12(x+5)=10(x+15)
解: 12x+60=10x+150
12x-10x=150-60
2x=90
x=45
7(x-2)=5(x+5)+9
解:7x-14=5x+25+9
7x-14=5x+34
2x=48
x=24
北师版四年级数学下册
认识方程
整理与复习(1)
汇报人:XXX 时间:XXXXX
小组交流:本单元主要学习了哪些内容?
认识方程
字母表示数
方程的意义
列方程解决问题
等式的性质
解方程
知识梳理
02
03
我们用字母表示数时,要注意字母的取值范围。其取值范围是由实际情况决定的。
01
像a,x,n,m……这样的字母或□、△……这样的符号都可以用来表示数
用字母或含有字母的式子不仅可以表示一个数量,还可以表示数量关系。
重点回顾
1.字母表示数
(①用字母表示数和数量关系)
1. 填一填。
(1)公共汽车上原来有x人,在青少年宫站有5人上车,又有6人下车,现在车上有乘客( )人。
(2)一本故事书98页,平均每天看x页,看了6天,还剩( )页。一本《数学竞赛》a元,买5本要( )元。
(3)一个两位数,十位上的数字是a,个位上的数字是b,那么这个两位数用( )表示。
x+5-6
98-6x
5a
10a+b
+5
-6
6x
a个10
b个1
用字母不仅可以表示一个数,还可以表示几个数量之间的关系。
2.你能说出下面含有字母的式子所表示的意思吗?
a元/块 b元/盒
(1)2a+b表示
(2)3b表示
(3)2(a-b)表示
2块面包和1盒牛奶的总价。
3盒牛奶的总价。
2块面包比2盒牛奶多多少元。
(答案不唯一)
(说明:a>b)
(4)3a+2b表示 ;
(5)10(a+b)表示 ;
(6)10(a-b)表示 。
3本书和2支钢笔一共多少元
10本书和10支钢笔一共多少元
10本书比10支钢笔贵多少元
02
03
用字母表示计算公式和运算定律比文字叙述更简明易记、便于应用。
01
在含有字母的式子里,数字和字母中间的乘号可以记作“·” ,也可以省略不写,但数字必须写在字母的前边。
a 读作a的平方,表示两个a 相乘,2a表示两个a相加。
1.字母表示数
②(用字母表示公式和运算律)
重点回顾
3. 省略乘号并化简下列各式。
3×x = m×52 = n×8 = x×y×z =
7×y+8×y = 2a+3a+6 =
12×x-7×x = 2.5×c-c =
3x
52m
8n
xyz
15y
5a+6
5x
1.5c
在用字母表示的式子里,乘号可以用“·”代替,或省略不写;利用乘法的分配律还可以对一些较复杂的式子进行化简。
4. 填一填,说一说。
用字母可以表示我们学过的运算律、运算性质、计算公式以及常用的数量关系。
(15.5+x)+9=15.5+( + )
7.5×a+2.5×a=a×( )
35-x-y=35 -( + )
s=v×( )
S平行四边形=a×( )
9
7.5+2.5
x
y
t
加法结合律
乘法分配律
x
连减的性质
速度、时间和路程的关系
h
平行四边形面积公式
运算律 用字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
α+b+c=α+(b+c)
α×b=b×α
(α×b)×c=α×(b×c)
(α+b)×c=α×c+b×c
α+b=b+α
α·b=b·α或αb=bα
(α·b)·c=α·(b·c)或(αb)c=α(bc)
(α+b)·c=α·c+b·c或(α+b)c=αc+bc
用字母表示运算定律,简明易记、便于应用。
运算律 用语言描述
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
两个数相加,交换加数的位置,和不变。
三个数相加,先把前两个数相加,或者先
把后两个数相加,结果不变。
两个数相乘,交换因数的位置,积不变。
三个数相乘,先把前两个数相乘,或者先
把后两个数相乘,结果不变。
两个数的和同一个数相乘,可以先把这两个加数
分别同这个数相乘,再把两个积相加,结果不变。
运算律 用字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
α+b+c=α+(b+c)
α+b=b+α
α·b=b·α或αb=bα
(α·b)·c=α·(b·c)或(αb)c=α(bc)
(α+b)·c=α·c+b·c或(α+b)c=αc+bc
02
03
方程一定是等式。等式不一定是方程。
01
含有未知数的等式,叫作方程。
方程要具备两个条件:
(1)含有未知数,(2)是等式。
重点回顾
2.方程的意义
等式
方程
这些等式有什么特点?与同伴进行交流。
2000=2z+200
4y=2000
10=x+2
用等号将相等的量连接起来,表示相等关系的
式子就是等式。
等式
像200+2z=2000,4y=2000 10=x+2 这样,根据等量关系列出的含有未知数的等式就是方程。
等式
未知数
不等式
x+ 20 <100
x + 20 > 50
10 < 100
等式
不含未知数
100+100=200
x + 20 = 70
方程
2 x = 150
3 x + 10 = 100
x + 10 = 15
分类整理
含有未知数
5.选一选。
下列式子中,等式有( C )个,方程有( B )个。
①2x+8 ②a+1.5=7 ③48+16=64
④6x+7=25
C
B
⑤2y-1.8>4.2 ⑥6a2=24
A.2 B.3 C.4
解析:含有等号的式子就是等式,②③④⑥是等式;含有未知数的等式才是方程,②④⑥是方程。
6.看图列方程。
(1)
70+x=100
(2)
3x+100=220
3a+156=208
解析:由图可知,3个a米加上156米等于208米,据此列出方程。
(3)
02
01
等式两边加上或减去同一个数,左右两边仍然相等。
等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
重点回顾
3.等式的性质
7.想一想,填一填,你发现了什么?
(1) 因为60-20=40,所以60-20+20=40+( 20 )。
(2) 因为x+2.4=10,所以x+2.4-2.4=10-( 2.4 )。
我发现:等式两边都加上(或减去)( 同一个 ),等式仍然成立。
20
2.4
同一个数
(3)在 里填上适当的运算符号,在 内填上适当的数,使天
平平衡。
+
10
20.5
-
8.在 里填上运算符号,在 里填上合适的数。
(1) 4x=12 4x÷4=12 ÷ 4
(2) x÷7=15 x÷7×7=15 × 7
我发现:等式两边都( 乘 )同一个数或( 除以 )同一个不为0的数,等式仍然成立。
÷
4
×
7
乘
除以
02
03
解方程的格式:先写解,点上冒号,等号对齐。
01
使方程左右两边相等的未知数的值,叫做方程的解;
求方程的解的过程叫做解方程;
重点回顾
4.解方程
23+x = 45
解: 23+x-23
=
45-23
x
=
22
“方程的解”中的“解”字是名词,表示一个具体的数;
“解方程”中的“解”字是动词,指求出方程的解的过程。
使方程左右两边相等的未知数的值,叫做方程的解。
求方程解的过程叫做解方程。
解方程的一般步骤
① 先写“解:”
②根据等式的性质使等式两边发生变化,使左边只含有未知数
③ 求出未知数的值
④ 检验
解方程。
-7=12
解:
-7+7=12+7
=19
第二行起
写“解”
等号对齐
x=19是不是正确的答案呢?检验一下。
方程左边=y-7
=19-7
=12
=方程右边
所以,x=19是方程的解。
检验时,如果方程左边不等于右边,
就说明这个值不是方程的解。
19-7=12, =19对了。
1.形如x±ɑ=b的方程的解法
x+a=b x-a=b
解: x+a-a=b-a 解:x-a+a=b+a
x=b-a x=b+a
a-x=b
解:a-x+x=b+x
a=b+x
x+b=a
x+b-b=a-b
x=a-b
ɑx=b x÷a =b
解:ax÷a =b÷ɑ 解:x÷a×a =b×ɑ
x =b÷ɑ x =b×ɑ
a÷x=b
解:a÷x×x=b×x
a=b×x
b×x=a
b×x÷b=a÷b
x=a÷b
2.形如ɑx=b和x÷a =b的方程的解法
9. 解方程并检验。
(1)18+x=32
解: 18+x-18=32-18
x=14
方程左边 =18+x
=18+14
=32
=方程右边
所以,x=14是方程的解。
检验
(2)x-13.4=6.8
解: x-13.4+13.4=6.8+13.4
x=20.2
方程左边 =x-13.4
=20.2 -13.4
=6.8
=方程右边
所以,x=20.2是方程的解。
检验
x=11
解:20-x+x=9+x
20=9+x
9+x=20
9+x-9=20-9
(3)20-x = 9。
方程左边=20-x
= 20-11
=9
=方程右边
所以,x=11是方程的解。
检验
交流小结:解方程需要注意什么?
1.解方程的依据是等式的性质1,解答时要注意格式,
还要记得检验。
2.加法、最简单:
加几就减去几。
3.减法、要注意:
x在前,很简单。减去几就加几。
x在后,挺麻烦。先消x后消数,中间还需调个头。
(4)5x=1.5
解:5x÷5=1.5÷5
x=0.3
方程左边=5x
=5×0.3
=1.5
=方程右边
所以,x=0.3是方程的解。
检验
解:x÷1.1×1.1=3×1.1
x=3.3
(5)x÷1.1=3
方程左边=x÷1.1
=3.3÷1.1
=3
=方程右边
所以,x=3.3是方程的解。
检验
x=7
解:21÷x×x=3×x
21=3×x
3×x=2.1
3x÷3=21÷3
(6)21÷x = 3
方程左边=21÷x
= 21÷7
=3
=方程右边
所以,x =7是方程的解。
检验
交流小结:解方程需要注意什么?
1.解方程的依据是等式的性质2,解答时要注意格式,
还要记得检验。
2.乘法最简单:
乘几就除以几。
3.除法要注意:
x在前,很简单。;除以几就乘几。
x在后,挺麻烦。先消x后消数,中间还需调个头。
老师告诉你:
解稍复杂的方程,一般运用等式的性质。但当未知数
是减数或除数时,运用减法或除法各部分之间的关系去解
相对简单。对于有些稍复杂的方程,还要先运用乘法分配
律将方程中的式子展开,再运用等式的性质去解。另外,
要判断所解方程是否正确,解方程后还要进行检验。
拓展延伸
解方程:3(x-15)-15=2x-10
例
思路分析:这个方程的左边有括号,先运用乘法分配律将左边展开得3x-45-15,再合并得3x-60,原方程就变成了3x-60=2x-10,最后运用等式的性质去解。等式两边都是减法,要先看减得多的,因此,等式两边同时加上60,方程变成3x=2x+50,再将等式两边同时减去2x,即得方程的解为x=50。
规范解答: 3(x-15)-15=2x-10
解:3x-45-15=2x-10
3x-60=2x-10
3x=2x+50
x=50
技巧1
运用各部分的关系解方程
1.解方程。
54-3x=24
解:3x=30
x=10
78-4x=22
解:4x=56
x=14
96÷(2x)=12
解:2x=8
x=4
120÷(4x)=5
解:4x=24
x=6
技巧2
运用等式的性质解方程
2.解方程。
3x+1.2×5=48
解: 3x+6=48
3x=42
x=14
8x-27÷3=15
解:8x-9=15
8x=24
x=3
8x-3=7x+3
解:8x-7x=3+3
x=6
5x+24=4x×2
解: 5x+24=8x
8x-5x=24
3x=24
x=8
解:2x=12
x=6
12-6x=8-2x
解:4x=4
x=1
6x-8=4x+4
技巧3
运用乘法分配律解方程
3.解方程。
8(18-x)-5x=53
解:144-8x-5x=53
144-13x=53
13x=91
x=7
4(x-2)=3(x+3)
解: 4x-8=3x+9
4x-3x=9+8
x=17
2(x-13)=(x+8×2)+13
解: 2x-26=x+16+13
2x-26=x+29
x=55
3(x-8)-6=2(x-8)
解: 3x-24-6=2x-16
3x-30=2x-16
x=14
12(x+5)=10(x+15)
解: 12x+60=10x+150
12x-10x=150-60
2x=90
x=45
7(x-2)=5(x+5)+9
解:7x-14=5x+25+9
7x-14=5x+34
2x=48
x=24
