四年级下册数学北师大版第五单元 认识方程 整理与复习(2)(课件)(共42张PPT)
文档属性
| 名称 | 四年级下册数学北师大版第五单元 认识方程 整理与复习(2)(课件)(共42张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-07 15:11:06 | ||
图片预览










文档简介
(共42张PPT)
北师版四年级数学下册
认识方程
整理与复习(2)
汇报人:XXX 时间:XXXXX
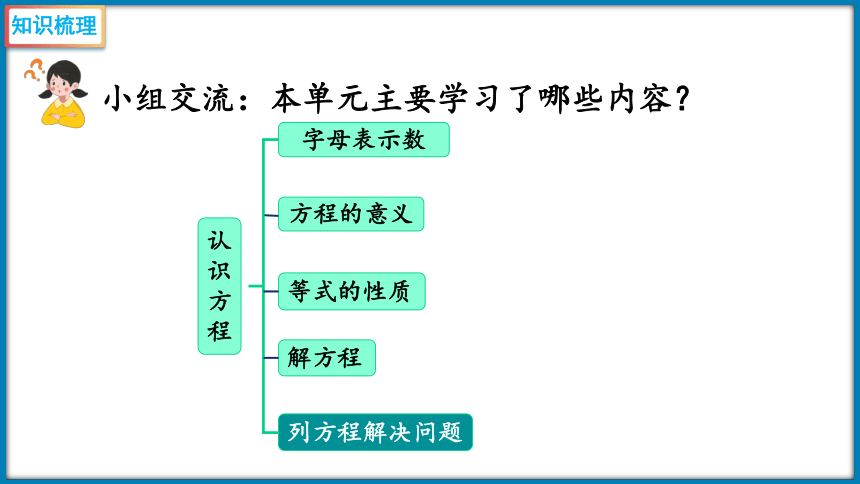
小组交流:本单元主要学习了哪些内容?
认识方程
字母表示数
方程的意义
列方程解决问题
等式的性质
解方程
知识梳理
小组讨论:
1.列方程解决问题的步骤什么?
列方程解决问题的步骤
弄清题意,找出未知数,用x表示;
分析、找出题中数量之间的相等关系,列方程;
解方程;
检验,并写出答语。
列方程解决实际问题
小组讨论:
2.怎样找到数量之间的相等关系?
确定等量关系常用的方法
根据题中反映的基本数量关系确定等量关系;
紧扣几何图形周长、面积和体积公式确定等量关系;
根据常见的数量关系确定等量关系;
抓住“不变量”确定等量关系。
列方程解决实际问题
(1)相差关系的实际问题,有两种列方程的方法,即x ±a=b
和b± x =a的形式;
(2)倍数关系的实际问题,通常依据“一倍数×倍数=几倍数”
或“几倍数÷倍数=一倍数”列方程。
(3)甲比乙的几倍多(或少)几,已知甲,求乙的问题,可
设乙为x ,根据乙×倍数±几=甲,列出形如ax±b=c的方
程进行求解。
小组讨论:
3.实际应用中可能存在哪些等量关系式?.
1.请根据等量关系或方程补充一个数学信息。
① 一个音乐盒90元, ,买一个音乐盒和一只玩具熊共用去138元。
等量关系:买一个音乐盒的钱数+买一只玩具熊的钱 数=一共用去的钱数
一只玩具熊48元
② 荣老师买了5盒水彩笔,每盒m元, ,找回2元。
方程:5m+2=100
付给售货员100元
解析:①根据已知信息可知,缺少买一只玩具熊的钱数,通过计算
可知一只玩具熊的价钱是138-90=48(元),据此补充信息即可;
②根据已知信息可知,5盒水彩笔是5m元,根据“买东西的钱数+
找回的钱数=付的钱数”补充信息即可。
③荣老师带3名学生去参观动物园,4张门票共20元,成人
票每张8元,学生票每张多少元?设学生票每张x元,列
方程得( 3x+8=20 )。
解析:由题意可得,3名学生买票花的钱数+老师买票花的钱数=总价。学生票每张x元,3名学生需要花3x元,加上老师的成人票8元,一共20元,据此列出方程:3x+8=20。
3x+8=20
④妈妈买了6千克苹果和2千克葡萄,花了42元,苹果每千
克4.5元,葡萄每千克x元。用方程计算每千克葡萄的价
格,列方程得( 2x+4.5×6=42 )。
解析:根据题意可得,买葡萄花的钱数+买苹果花的钱数=一共花的钱数。因为葡萄每千克x元,买2千克花2x元,苹果每千克4.5
元,买6千克花4.5×6元,则买6千克苹果和2千克葡萄一共花了(2x+4.5×6)元,即2x+4.5×6=42。
2x+4.5×6=42
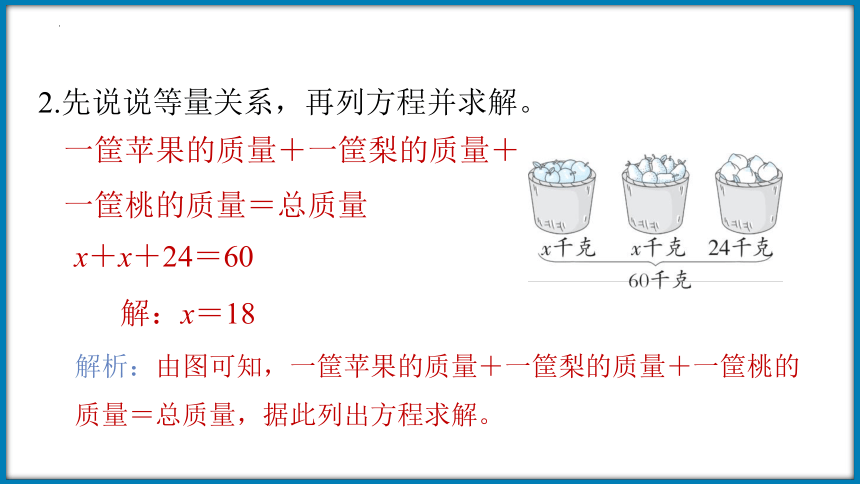
2.先说说等量关系,再列方程并求解。
一筐苹果的质量+一筐梨的质量+
一筐桃的质量=总质量
x+x+24=60
解:x=18
解析:由图可知,一筐苹果的质量+一筐梨的质量+一筐桃的质量=总质量,据此列出方程求解。
(1)
3x+18=19.8
解析:由图可知,3支铅笔的价钱和1个文具盒的价钱相加等于19.8元,据此列出方程即可;
3.看图列方程,并解方程。
(2)
x+4x=90
解析:由图可知,女生人数+男生人数=90人,据此列出方程即可。
x+3x+3=27
解:x=6
解析:由图可知,沙包的个数+毽子的个数=27个,其中沙包的个数×3+3个=毽子的个数,据此列出方程并解答。
(3)
4.下面是一张撕掉一部分的发票,你能算出每瓶墨水多少
元吗?(列方程解答)
解:设每瓶墨水x元。
1.5+12x=25.5
x=2
答:每瓶墨水2元。
5.先写出等量关系式,再列方程解答。
手工课上,四(1) 班女生做了283颗幸运星,如果再做37
颗,就是男生做的数量的2倍。男生做了多少颗幸运星?
男生做的数量×2=女生做的数量+37颗
解:设男生做了x颗幸运星。
2x=283+37
x=160
答:男生做了160颗幸运星。
解析:根据题意可知,男生做的数量×2=女生做的数量+37颗,根据这一等量关系可设男生做了x颗幸运星,列出方程求解即可。
6.故宫博物院的面积是72万平方米,比天安门广场面积的
2倍少16万平方米。天安门广场的面积是多少万平方米?
解:设天安门广场的面积是x万平方米。
2x-16=72
x=44
答:天安门广场的面积是44万平方米。
解析:根据题意可知,天安门广场的面积×2-16万平方米=故宫博物院的面积,设天安门广场的面积是x万平方米,列出方程解答即可。
老师告诉你:
列方程解决问题的一般方法:
1.弄清题意,确定未知数并用x表示;
2.找出题中的等量关系,列出方程并解答;
3.检验,检查方程的解是否正确及所求得的未知数的值是
否符合题意。
拓展延伸
解析:根据已知条件可知,文件夹1.5元/个,买了1个,墨水买了12
瓶,共花了25.5元。根据题意,设每瓶墨水x元,根据单价×数量
=总价,买墨水的总价+买文件夹的总价=合计数,列出方程,再
解方程求出答案。
有一个两层的书架,上层放的书的数量是下层的3
倍,如果把上层的书取60本放到下层,则两层的书的数量相等。原来上、下层各有多少本书?
例
思路分析:解答本题时,我们要抓住“如果把上层的书取60本放到下层,则两层的书的数量相等”这一等量关系建立方程。在设未知数时,一般设较小的数为x,本题可设原来下层有x本书,然后列出方程解答。
规范解答:解:设原来下层有x本书,则原来上层有3x
本书。
3x-60=x+60
3x-x=60+60
2x=120
x=60
上层:60×3=180(本)
答:原来上层有180本书,下层有60本书。
2
1
5
3
列方程解决倍数问题
列方程解决行程问题
列方程解决数的组成问题
列方程解决两个量之间的变化问题
类型1
列方程解决倍数问题
1.红星水果店里橘子的质量是苹果的3倍,如果每天卖30千克苹果和60千克橘子,若干天后,苹果全部卖完,橘子还剩120千克。红星水果店原来有橘子多少千克?
解:设卖了x天后,苹果全部卖完。
60x+120=30x×3
x=4
橘子:60×4+120=360(千克)
答:红星水果店原来有橘子360千克。
类型2
列方程解决行程问题
2.甲地与乙地相距315千米,一辆轿车和一辆货车同时从两地相向开出,轿车每时行驶60千米,3时后两车相距15千米。货车每时行驶多少千米?(画图并列方程解答) (画图略)
(画图略)
解:设货车每时行驶x千米。
3(60+x)+15=315 或3(60+x)=315+15
x=40 x=50
答:货车每时行驶40千米或50千米。
类型3
列方程解决数的组成问题
3.有一个两位数,十位上的数字是个位上数字的2倍,如果把这两个数字的位置对调,那么所得的新数比原数小
27。这个两位数原来是多少?
解析:用字母表示各数位上的数字时,要乘该数位上的计数单位。
等量关系:原数-新数=27。
类型4
列方程解决两个量之间的变化问题
4.有甲、乙两个书架,若从甲书架取出8本书放到乙书架,两个书架上的书就一样多;若从乙书架取出13本书放到甲书架,甲书架上书的数量就是乙书架上的2倍。甲、乙两个书架上原来各有多少本书?
解:设乙书架上原来有x本书,则甲书架上原来有
(x+8×2)本书。
2(x-13)=x+8×2+13
x=55
甲书架:55+8×2=71(本)
答:甲书架上原来有71本书,乙书架上原来有55本书。
5.甲、乙两个仓库存有货物,若从甲仓库取出15吨放入乙
仓库,则两个仓库存的货物一样多;若从乙仓库取出6吨
放入甲仓库,则甲仓库货物的质量是乙仓库的3倍。甲、
乙两个仓库原来各存货物多少吨?
解:设乙仓库原来存货物x吨,则甲仓库原来存货物
(x+15×2)吨。
3(x-6)=x+15×2+6
x=27
甲仓库:27+15×2=57(吨)
答:甲仓库原来存货物57吨,乙仓库原来存货物27吨。
老师告诉你:
用方程法解“鸡兔同笼”问题、盈亏问题等典型应用
题时,只要准确找出题目中的等量关系,就能正确地列出
方程进行解答。鸡兔同笼问题的等量关系式是“鸡的脚数
+兔的脚数=总脚数”;盈亏问题可以根据待分物品的总
数不变列方程。
拓展延伸
小明给班里买了甲、乙两种电影票共50张,甲种票
每张20元,乙种票每张14元,一共花了784元。甲、乙两种票各买了多少张?
例
思路分析:根据题意可知等量关系式:买甲种票的钱+买乙种票的钱=一共花的钱。为了计算时方便,一般设贵的票买了x张,所以设甲种票买了x张,则乙种票买了(50-x)张,根据上面的等量关系式列方程解答即可。
规范解答:解:设甲种票买了x张,则乙种票买了
(50-x)张。
20x+14(50-x)=784
20x+700-14x=784
6x=84
x=14
50-14=36(张)
答:甲种票买了14张,乙种票买了36张。
2
1
3
4
列方程解决“鸡兔同笼”类问题
列方程解决盈亏问题
列方程解决行船问题
列方程解决追及问题
类型1
列方程解决“鸡兔同笼”类问题
1.有2元和5元的代金券共36张,总面值为99元。这两种代
金券各有多少张?
解析:等量关系式:2元代金券的总面值+5元代金券的总面值=99元。
解:设5元的代金券有x张。
5x+2(36-x)=99
5x+72-2x=99
x=9
36-9=27(张)
答:5元的代金券有9张,2元的代金券有27张。
2.动物园里有仙鹤和长颈鹿共17只,共有54条腿。仙鹤、
长颈鹿各有多少只?
解:设长颈鹿有x只。
4x+2(17-x)=54
4x+34-2x=54
x=10
17-10=7(只)
答:长颈鹿有10只,仙鹤有7只。
3.全班46人去划船,共乘12条船。其中,每条大船坐5
人,每条小船坐3人(大、小船全部坐满)。大、小船各
有多少条?
解:设大船有x条。
5x+3(12-x)=46
5x+36-3x=46
x=5 12-5=7(条)
答:大船有5条,小船有7条。
类型2
列方程解决盈亏问题
4.美术课上,老师给表现优秀的小朋友分糖,如果每人分4颗糖,就多5颗;如果每人分5颗糖,就少4颗。表现优秀的小朋友有多少人?
解:设表现优秀的小朋友有x人。
4x+5=5x-4
x=9
答:表现优秀的小朋友有9人。
点拨:本题根据糖的总数不变列方程解答。
5.一个植树小组植树,如果每人植3棵,还剩14棵;如果每
人植5棵,还剩2棵。这个植树小组有多少人?一共有多
少棵树?
解:设这个植树小组有x人。
3x+14=5x+2
x=6 3×6+14=32(棵)
答:这个植树小组有6人,一共有32棵树。
类型3
列方程解决行船问题
6.一条船在两个码头之间航行,顺水行全程要4时,逆水行全程要5时,已知水流的速度是2千米/时。这条船在静水中的速度是多少?
解:设这条船在静水中的速度是x千米/时。
4×(x+2)=5×(x-2)
x=18
答:这条船在静水中的速度是18千米/时。
点拨:本题根据路程不变列方程解答。
类型4
列方程解决追及问题
7.一条环形跑道长400米,明明每分跑260米,亮亮每分跑
210米。两人同时同地同向出发,经过多少分后明明第一次追上亮亮?
解:设经过x分后明明第一次追上亮亮。
(260-210)x=400
x=8
答:经过8分后明明第一次追上亮亮。
解析:“第一次追上”说明明明比亮亮多跑一圈,本题根据追及问题的关系式列方程解答。
早在3600多年前,古埃及纸草书中有相当于解简单一次方程的问题。在我国,成书于公元1世纪前后的《九章算术》中就有了用一组方程解决问题的记载,可以说《九章算术》已有方程的思想。12世纪前后,我国数学家开始用专门的记号来表示未知数。
北师版四年级数学下册
认识方程
整理与复习(2)
汇报人:XXX 时间:XXXXX
小组交流:本单元主要学习了哪些内容?
认识方程
字母表示数
方程的意义
列方程解决问题
等式的性质
解方程
知识梳理
小组讨论:
1.列方程解决问题的步骤什么?
列方程解决问题的步骤
弄清题意,找出未知数,用x表示;
分析、找出题中数量之间的相等关系,列方程;
解方程;
检验,并写出答语。
列方程解决实际问题
小组讨论:
2.怎样找到数量之间的相等关系?
确定等量关系常用的方法
根据题中反映的基本数量关系确定等量关系;
紧扣几何图形周长、面积和体积公式确定等量关系;
根据常见的数量关系确定等量关系;
抓住“不变量”确定等量关系。
列方程解决实际问题
(1)相差关系的实际问题,有两种列方程的方法,即x ±a=b
和b± x =a的形式;
(2)倍数关系的实际问题,通常依据“一倍数×倍数=几倍数”
或“几倍数÷倍数=一倍数”列方程。
(3)甲比乙的几倍多(或少)几,已知甲,求乙的问题,可
设乙为x ,根据乙×倍数±几=甲,列出形如ax±b=c的方
程进行求解。
小组讨论:
3.实际应用中可能存在哪些等量关系式?.
1.请根据等量关系或方程补充一个数学信息。
① 一个音乐盒90元, ,买一个音乐盒和一只玩具熊共用去138元。
等量关系:买一个音乐盒的钱数+买一只玩具熊的钱 数=一共用去的钱数
一只玩具熊48元
② 荣老师买了5盒水彩笔,每盒m元, ,找回2元。
方程:5m+2=100
付给售货员100元
解析:①根据已知信息可知,缺少买一只玩具熊的钱数,通过计算
可知一只玩具熊的价钱是138-90=48(元),据此补充信息即可;
②根据已知信息可知,5盒水彩笔是5m元,根据“买东西的钱数+
找回的钱数=付的钱数”补充信息即可。
③荣老师带3名学生去参观动物园,4张门票共20元,成人
票每张8元,学生票每张多少元?设学生票每张x元,列
方程得( 3x+8=20 )。
解析:由题意可得,3名学生买票花的钱数+老师买票花的钱数=总价。学生票每张x元,3名学生需要花3x元,加上老师的成人票8元,一共20元,据此列出方程:3x+8=20。
3x+8=20
④妈妈买了6千克苹果和2千克葡萄,花了42元,苹果每千
克4.5元,葡萄每千克x元。用方程计算每千克葡萄的价
格,列方程得( 2x+4.5×6=42 )。
解析:根据题意可得,买葡萄花的钱数+买苹果花的钱数=一共花的钱数。因为葡萄每千克x元,买2千克花2x元,苹果每千克4.5
元,买6千克花4.5×6元,则买6千克苹果和2千克葡萄一共花了(2x+4.5×6)元,即2x+4.5×6=42。
2x+4.5×6=42
2.先说说等量关系,再列方程并求解。
一筐苹果的质量+一筐梨的质量+
一筐桃的质量=总质量
x+x+24=60
解:x=18
解析:由图可知,一筐苹果的质量+一筐梨的质量+一筐桃的质量=总质量,据此列出方程求解。
(1)
3x+18=19.8
解析:由图可知,3支铅笔的价钱和1个文具盒的价钱相加等于19.8元,据此列出方程即可;
3.看图列方程,并解方程。
(2)
x+4x=90
解析:由图可知,女生人数+男生人数=90人,据此列出方程即可。
x+3x+3=27
解:x=6
解析:由图可知,沙包的个数+毽子的个数=27个,其中沙包的个数×3+3个=毽子的个数,据此列出方程并解答。
(3)
4.下面是一张撕掉一部分的发票,你能算出每瓶墨水多少
元吗?(列方程解答)
解:设每瓶墨水x元。
1.5+12x=25.5
x=2
答:每瓶墨水2元。
5.先写出等量关系式,再列方程解答。
手工课上,四(1) 班女生做了283颗幸运星,如果再做37
颗,就是男生做的数量的2倍。男生做了多少颗幸运星?
男生做的数量×2=女生做的数量+37颗
解:设男生做了x颗幸运星。
2x=283+37
x=160
答:男生做了160颗幸运星。
解析:根据题意可知,男生做的数量×2=女生做的数量+37颗,根据这一等量关系可设男生做了x颗幸运星,列出方程求解即可。
6.故宫博物院的面积是72万平方米,比天安门广场面积的
2倍少16万平方米。天安门广场的面积是多少万平方米?
解:设天安门广场的面积是x万平方米。
2x-16=72
x=44
答:天安门广场的面积是44万平方米。
解析:根据题意可知,天安门广场的面积×2-16万平方米=故宫博物院的面积,设天安门广场的面积是x万平方米,列出方程解答即可。
老师告诉你:
列方程解决问题的一般方法:
1.弄清题意,确定未知数并用x表示;
2.找出题中的等量关系,列出方程并解答;
3.检验,检查方程的解是否正确及所求得的未知数的值是
否符合题意。
拓展延伸
解析:根据已知条件可知,文件夹1.5元/个,买了1个,墨水买了12
瓶,共花了25.5元。根据题意,设每瓶墨水x元,根据单价×数量
=总价,买墨水的总价+买文件夹的总价=合计数,列出方程,再
解方程求出答案。
有一个两层的书架,上层放的书的数量是下层的3
倍,如果把上层的书取60本放到下层,则两层的书的数量相等。原来上、下层各有多少本书?
例
思路分析:解答本题时,我们要抓住“如果把上层的书取60本放到下层,则两层的书的数量相等”这一等量关系建立方程。在设未知数时,一般设较小的数为x,本题可设原来下层有x本书,然后列出方程解答。
规范解答:解:设原来下层有x本书,则原来上层有3x
本书。
3x-60=x+60
3x-x=60+60
2x=120
x=60
上层:60×3=180(本)
答:原来上层有180本书,下层有60本书。
2
1
5
3
列方程解决倍数问题
列方程解决行程问题
列方程解决数的组成问题
列方程解决两个量之间的变化问题
类型1
列方程解决倍数问题
1.红星水果店里橘子的质量是苹果的3倍,如果每天卖30千克苹果和60千克橘子,若干天后,苹果全部卖完,橘子还剩120千克。红星水果店原来有橘子多少千克?
解:设卖了x天后,苹果全部卖完。
60x+120=30x×3
x=4
橘子:60×4+120=360(千克)
答:红星水果店原来有橘子360千克。
类型2
列方程解决行程问题
2.甲地与乙地相距315千米,一辆轿车和一辆货车同时从两地相向开出,轿车每时行驶60千米,3时后两车相距15千米。货车每时行驶多少千米?(画图并列方程解答) (画图略)
(画图略)
解:设货车每时行驶x千米。
3(60+x)+15=315 或3(60+x)=315+15
x=40 x=50
答:货车每时行驶40千米或50千米。
类型3
列方程解决数的组成问题
3.有一个两位数,十位上的数字是个位上数字的2倍,如果把这两个数字的位置对调,那么所得的新数比原数小
27。这个两位数原来是多少?
解析:用字母表示各数位上的数字时,要乘该数位上的计数单位。
等量关系:原数-新数=27。
类型4
列方程解决两个量之间的变化问题
4.有甲、乙两个书架,若从甲书架取出8本书放到乙书架,两个书架上的书就一样多;若从乙书架取出13本书放到甲书架,甲书架上书的数量就是乙书架上的2倍。甲、乙两个书架上原来各有多少本书?
解:设乙书架上原来有x本书,则甲书架上原来有
(x+8×2)本书。
2(x-13)=x+8×2+13
x=55
甲书架:55+8×2=71(本)
答:甲书架上原来有71本书,乙书架上原来有55本书。
5.甲、乙两个仓库存有货物,若从甲仓库取出15吨放入乙
仓库,则两个仓库存的货物一样多;若从乙仓库取出6吨
放入甲仓库,则甲仓库货物的质量是乙仓库的3倍。甲、
乙两个仓库原来各存货物多少吨?
解:设乙仓库原来存货物x吨,则甲仓库原来存货物
(x+15×2)吨。
3(x-6)=x+15×2+6
x=27
甲仓库:27+15×2=57(吨)
答:甲仓库原来存货物57吨,乙仓库原来存货物27吨。
老师告诉你:
用方程法解“鸡兔同笼”问题、盈亏问题等典型应用
题时,只要准确找出题目中的等量关系,就能正确地列出
方程进行解答。鸡兔同笼问题的等量关系式是“鸡的脚数
+兔的脚数=总脚数”;盈亏问题可以根据待分物品的总
数不变列方程。
拓展延伸
小明给班里买了甲、乙两种电影票共50张,甲种票
每张20元,乙种票每张14元,一共花了784元。甲、乙两种票各买了多少张?
例
思路分析:根据题意可知等量关系式:买甲种票的钱+买乙种票的钱=一共花的钱。为了计算时方便,一般设贵的票买了x张,所以设甲种票买了x张,则乙种票买了(50-x)张,根据上面的等量关系式列方程解答即可。
规范解答:解:设甲种票买了x张,则乙种票买了
(50-x)张。
20x+14(50-x)=784
20x+700-14x=784
6x=84
x=14
50-14=36(张)
答:甲种票买了14张,乙种票买了36张。
2
1
3
4
列方程解决“鸡兔同笼”类问题
列方程解决盈亏问题
列方程解决行船问题
列方程解决追及问题
类型1
列方程解决“鸡兔同笼”类问题
1.有2元和5元的代金券共36张,总面值为99元。这两种代
金券各有多少张?
解析:等量关系式:2元代金券的总面值+5元代金券的总面值=99元。
解:设5元的代金券有x张。
5x+2(36-x)=99
5x+72-2x=99
x=9
36-9=27(张)
答:5元的代金券有9张,2元的代金券有27张。
2.动物园里有仙鹤和长颈鹿共17只,共有54条腿。仙鹤、
长颈鹿各有多少只?
解:设长颈鹿有x只。
4x+2(17-x)=54
4x+34-2x=54
x=10
17-10=7(只)
答:长颈鹿有10只,仙鹤有7只。
3.全班46人去划船,共乘12条船。其中,每条大船坐5
人,每条小船坐3人(大、小船全部坐满)。大、小船各
有多少条?
解:设大船有x条。
5x+3(12-x)=46
5x+36-3x=46
x=5 12-5=7(条)
答:大船有5条,小船有7条。
类型2
列方程解决盈亏问题
4.美术课上,老师给表现优秀的小朋友分糖,如果每人分4颗糖,就多5颗;如果每人分5颗糖,就少4颗。表现优秀的小朋友有多少人?
解:设表现优秀的小朋友有x人。
4x+5=5x-4
x=9
答:表现优秀的小朋友有9人。
点拨:本题根据糖的总数不变列方程解答。
5.一个植树小组植树,如果每人植3棵,还剩14棵;如果每
人植5棵,还剩2棵。这个植树小组有多少人?一共有多
少棵树?
解:设这个植树小组有x人。
3x+14=5x+2
x=6 3×6+14=32(棵)
答:这个植树小组有6人,一共有32棵树。
类型3
列方程解决行船问题
6.一条船在两个码头之间航行,顺水行全程要4时,逆水行全程要5时,已知水流的速度是2千米/时。这条船在静水中的速度是多少?
解:设这条船在静水中的速度是x千米/时。
4×(x+2)=5×(x-2)
x=18
答:这条船在静水中的速度是18千米/时。
点拨:本题根据路程不变列方程解答。
类型4
列方程解决追及问题
7.一条环形跑道长400米,明明每分跑260米,亮亮每分跑
210米。两人同时同地同向出发,经过多少分后明明第一次追上亮亮?
解:设经过x分后明明第一次追上亮亮。
(260-210)x=400
x=8
答:经过8分后明明第一次追上亮亮。
解析:“第一次追上”说明明明比亮亮多跑一圈,本题根据追及问题的关系式列方程解答。
早在3600多年前,古埃及纸草书中有相当于解简单一次方程的问题。在我国,成书于公元1世纪前后的《九章算术》中就有了用一组方程解决问题的记载,可以说《九章算术》已有方程的思想。12世纪前后,我国数学家开始用专门的记号来表示未知数。
