第二单元 认识三角形和四边形(同步练习)-2023-2024学年四年级数学下册北师大版(含答案)
文档属性
| 名称 | 第二单元 认识三角形和四边形(同步练习)-2023-2024学年四年级数学下册北师大版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 97.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-14 09:22:13 | ||
图片预览

文档简介
第二单元 认识三角形和四边形(同步练习)-2023-2024学年四年级数学下册北师大版
一、单选题
1.一个三角形,其中有两个角分别是50°和70°,第三个角是( )
A.50° B.60° C.70° D.80°
2.想要给一块菜地围上篱笆,围法最牢固的方案是( )。
A. B. C. D.
3.如果A点用数对表示为(2,5),B点用数对表示数(2,2),C点用数对表示为(4,2),那么三角形ABC一定是( )三角形。
A.锐角 B.钝角 C.直角 D.等腰
4. 一个等腰三角形其中一个角是50°,这个三角形( )。
A.一定是锐角三角形 B.有可能是锐角三角形
C.有可能是钝角三角形 D.无法确定
5.一个三角形的周长是36cm,那么它的任意两边的和可能是( )。
A.9厘米 B.18厘米 C.27厘米 D.36厘米
二、判断题
6.平行四边形容易变形。( )
7.一个等腰三角形的一个底角是a°,顶角是(180-2a)°。( )
8.等腰三角形一定是等边三角形。( )
9.把一个三角形分成两个小三角形,每个小三角形的内角和是90°。(
)
10.等边三角形的每一个内角都是60°。( )
三、填空题
11.从长度分别是1cm、3cm、5cm、7cm的4根小棒中,选3根组成一个三角形。这个三角形三条边的长分别是 cm、 cm、 cm。
12.三角形玻璃打碎了一个角(如图),打碎的这个角是 °。这块玻璃原来的形状是一个 三角形,还是一个 三角形。
13.如果三角形的两条边的长分别是5厘米和9厘米,且第三条边的长是整厘米数,那么第三条边的长最长是 厘米,最短是 厘米。
14.一个直角三角形的一个角是65°,另一个锐角是 °.
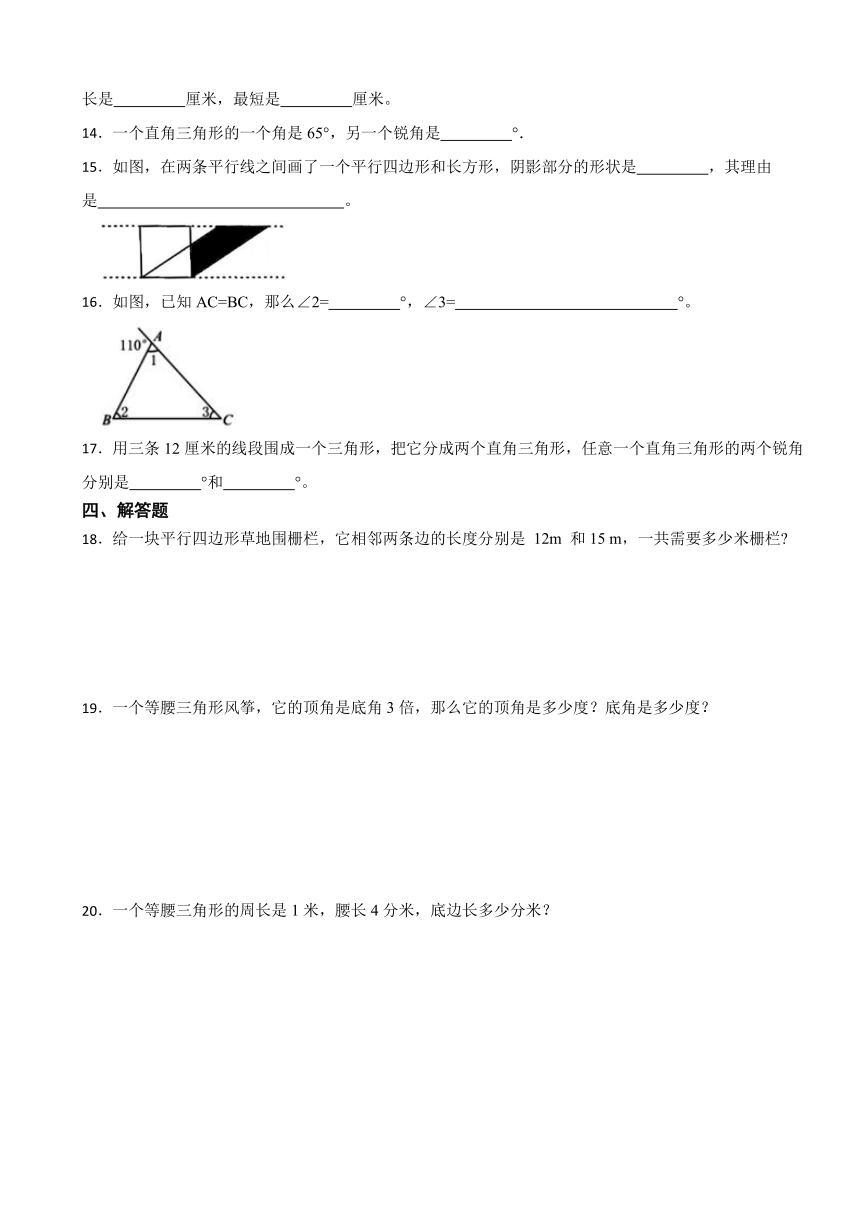
15.如图,在两条平行线之间画了一个平行四边形和长方形,阴影部分的形状是 ,其理由是 。
16.如图,已知AC=BC,那么∠2= °,∠3= °。
17.用三条12厘米的线段围成一个三角形,把它分成两个直角三角形,任意一个直角三角形的两个锐角分别是 °和 °。
四、解答题
18.给一块平行四边形草地围栅栏,它相邻两条边的长度分别是 12m 和15 m,一共需要多少米栅栏
19.一个等腰三角形风筝,它的顶角是底角3倍,那么它的顶角是多少度?底角是多少度?
20.一个等腰三角形的周长是1米,腰长4分米,底边长多少分米?
21.下面是三块三角形玻璃打碎后留下的碎片,你能判断出它们原来各是什么三角形吗?
22.三角形ABC是一个直角三角形,三角形BDC是一个等腰三角形,∠1=∠2,∠3=42°,求∠4的度数。
23.做风筝。
(1)做一个等腰三角形风筝。它的一个顶角是80°,它的一个底角是多少度?
(2)做一个等腰三角形风筝,它的一腰长是6dm,它的底边长的取值范围应在多少厘米之间?你的根据是什么?(取整厘米数,只考虑能否做成的因素,不考虑其它因素)
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】C
4.【答案】A
5.【答案】C
6.【答案】正确
7.【答案】正确
8.【答案】错误
9.【答案】错误
10.【答案】正确
11.【答案】3;5;8
12.【答案】70;锐角;等腰
13.【答案】13;5
14.【答案】25
15.【答案】梯形;这个四边形只有一组对边平行
16.【答案】70;40 (或乘10,扩大10倍)
17.【答案】60;30
18.【答案】解:(12+15)×2
=27×2
=54(米)
答:一共需要54米栅栏。
19.【答案】解:180°÷(3+2)
=180°÷5
=36°
36°×3=108°
答:顶角是108度,底角是36度。
20.【答案】解:10 -4×2=2(分米)
答:底边长2分米。
21.【答案】解:图一中打碎的那个角的度数是180°-30°-40°=110°,所以这个三角形原来是钝角三角形;
图二中打碎的那个角的度数是180°-60°-60°=60°,所以这个三角形原来是锐角三角形;
图三中打碎的那个角的度数是180°-50°-40°=90°,所以这个三角形原来是直角三角形。
22.【答案】解:90°-42°=48°
180°-48°×2
=180°-96°
=84°
答:∠4的度数是84°。
23.【答案】(1)解:(180°-80°)÷2
=100°÷2
=50°
答:它的一个底角是50度。
(2)解:底边长的取值范围应在:1厘米和11厘米之间,即可取1cm、2cm ..... 10cm、11 cm。根据任意三角形的两边之和大于第三边。
一、单选题
1.一个三角形,其中有两个角分别是50°和70°,第三个角是( )
A.50° B.60° C.70° D.80°
2.想要给一块菜地围上篱笆,围法最牢固的方案是( )。
A. B. C. D.
3.如果A点用数对表示为(2,5),B点用数对表示数(2,2),C点用数对表示为(4,2),那么三角形ABC一定是( )三角形。
A.锐角 B.钝角 C.直角 D.等腰
4. 一个等腰三角形其中一个角是50°,这个三角形( )。
A.一定是锐角三角形 B.有可能是锐角三角形
C.有可能是钝角三角形 D.无法确定
5.一个三角形的周长是36cm,那么它的任意两边的和可能是( )。
A.9厘米 B.18厘米 C.27厘米 D.36厘米
二、判断题
6.平行四边形容易变形。( )
7.一个等腰三角形的一个底角是a°,顶角是(180-2a)°。( )
8.等腰三角形一定是等边三角形。( )
9.把一个三角形分成两个小三角形,每个小三角形的内角和是90°。(
)
10.等边三角形的每一个内角都是60°。( )
三、填空题
11.从长度分别是1cm、3cm、5cm、7cm的4根小棒中,选3根组成一个三角形。这个三角形三条边的长分别是 cm、 cm、 cm。
12.三角形玻璃打碎了一个角(如图),打碎的这个角是 °。这块玻璃原来的形状是一个 三角形,还是一个 三角形。
13.如果三角形的两条边的长分别是5厘米和9厘米,且第三条边的长是整厘米数,那么第三条边的长最长是 厘米,最短是 厘米。
14.一个直角三角形的一个角是65°,另一个锐角是 °.
15.如图,在两条平行线之间画了一个平行四边形和长方形,阴影部分的形状是 ,其理由是 。
16.如图,已知AC=BC,那么∠2= °,∠3= °。
17.用三条12厘米的线段围成一个三角形,把它分成两个直角三角形,任意一个直角三角形的两个锐角分别是 °和 °。
四、解答题
18.给一块平行四边形草地围栅栏,它相邻两条边的长度分别是 12m 和15 m,一共需要多少米栅栏
19.一个等腰三角形风筝,它的顶角是底角3倍,那么它的顶角是多少度?底角是多少度?
20.一个等腰三角形的周长是1米,腰长4分米,底边长多少分米?
21.下面是三块三角形玻璃打碎后留下的碎片,你能判断出它们原来各是什么三角形吗?
22.三角形ABC是一个直角三角形,三角形BDC是一个等腰三角形,∠1=∠2,∠3=42°,求∠4的度数。
23.做风筝。
(1)做一个等腰三角形风筝。它的一个顶角是80°,它的一个底角是多少度?
(2)做一个等腰三角形风筝,它的一腰长是6dm,它的底边长的取值范围应在多少厘米之间?你的根据是什么?(取整厘米数,只考虑能否做成的因素,不考虑其它因素)
答案解析部分
1.【答案】B
2.【答案】A
3.【答案】C
4.【答案】A
5.【答案】C
6.【答案】正确
7.【答案】正确
8.【答案】错误
9.【答案】错误
10.【答案】正确
11.【答案】3;5;8
12.【答案】70;锐角;等腰
13.【答案】13;5
14.【答案】25
15.【答案】梯形;这个四边形只有一组对边平行
16.【答案】70;40 (或乘10,扩大10倍)
17.【答案】60;30
18.【答案】解:(12+15)×2
=27×2
=54(米)
答:一共需要54米栅栏。
19.【答案】解:180°÷(3+2)
=180°÷5
=36°
36°×3=108°
答:顶角是108度,底角是36度。
20.【答案】解:10 -4×2=2(分米)
答:底边长2分米。
21.【答案】解:图一中打碎的那个角的度数是180°-30°-40°=110°,所以这个三角形原来是钝角三角形;
图二中打碎的那个角的度数是180°-60°-60°=60°,所以这个三角形原来是锐角三角形;
图三中打碎的那个角的度数是180°-50°-40°=90°,所以这个三角形原来是直角三角形。
22.【答案】解:90°-42°=48°
180°-48°×2
=180°-96°
=84°
答:∠4的度数是84°。
23.【答案】(1)解:(180°-80°)÷2
=100°÷2
=50°
答:它的一个底角是50度。
(2)解:底边长的取值范围应在:1厘米和11厘米之间,即可取1cm、2cm ..... 10cm、11 cm。根据任意三角形的两边之和大于第三边。
