北师大版四年级下册第二单元《认识三角形和四边形》单元专项训练——图形计算题(含答案)
文档属性
| 名称 | 北师大版四年级下册第二单元《认识三角形和四边形》单元专项训练——图形计算题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 388.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-16 20:12:30 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二单元《认识三角形和四边形》单元专项训练——图形计算题
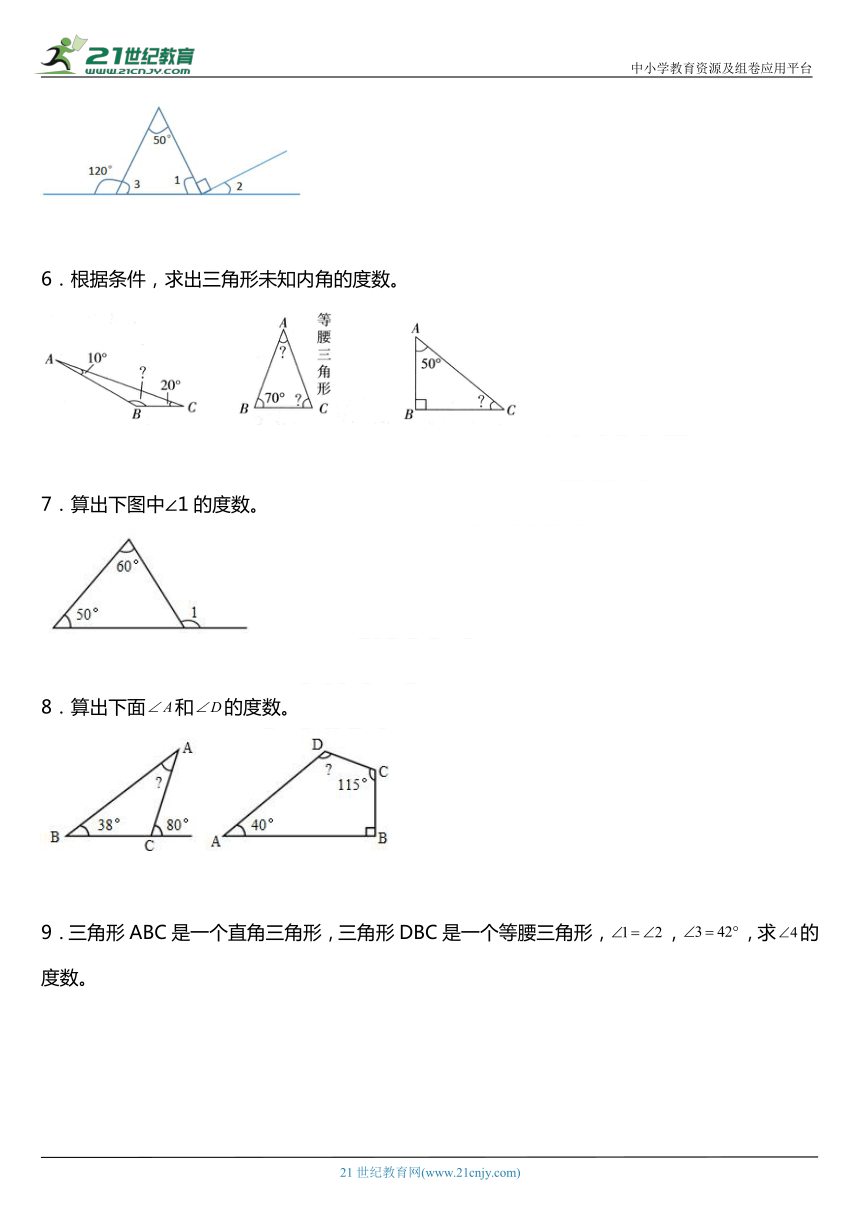
1.算一算。
,是直角。求的度数。
2.求出∠3的度数。
3.图形计算(计算各图形的周长)。
4.算出下面各个未知角的度数。
5.求∠1、∠2、∠3的度数。
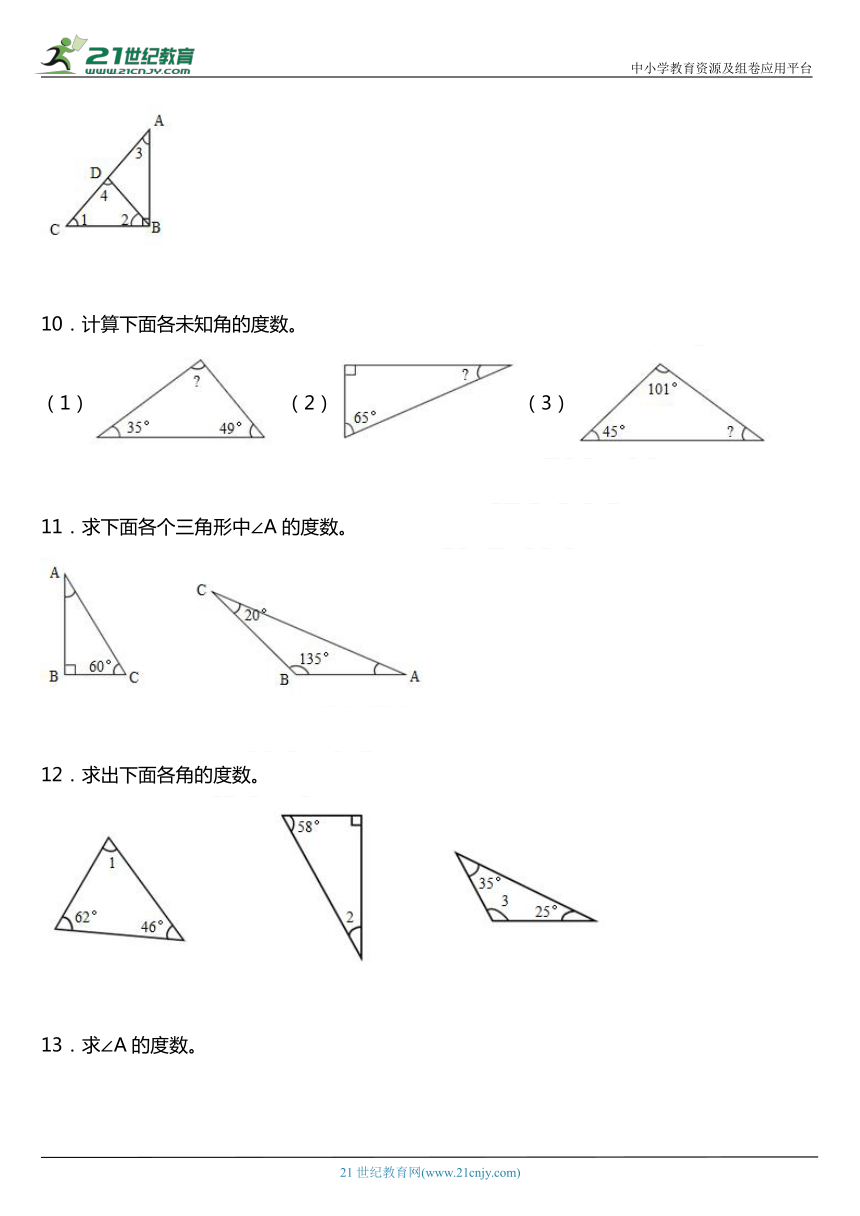
6.根据条件,求出三角形未知内角的度数。
7.算出下图中∠1的度数。
8.算出下面和的度数。
9.三角形ABC是一个直角三角形,三角形DBC是一个等腰三角形,,,求的度数。
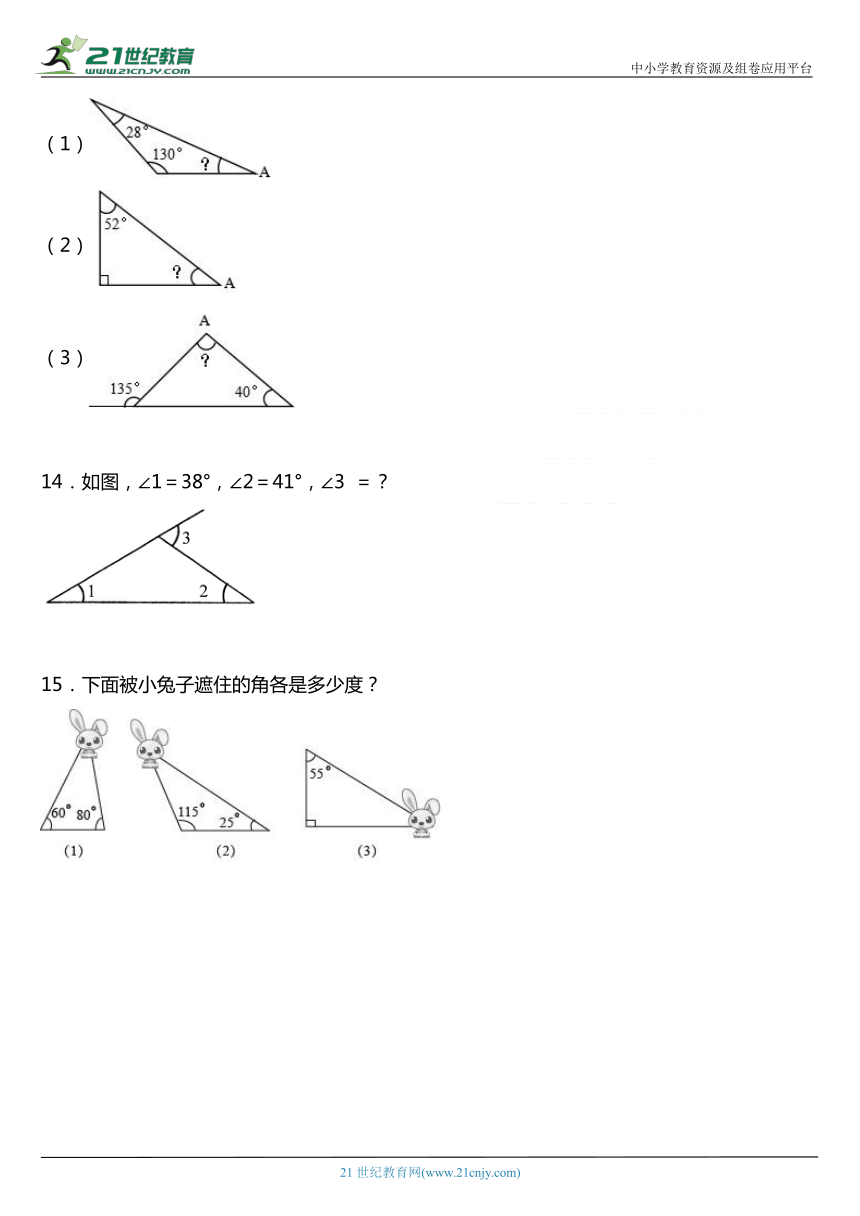
10.计算下面各未知角的度数。
(1) (2)(3)
11.求下面各个三角形中∠A的度数。
12.求出下面各角的度数。
13.求∠A的度数。
(1)
(2)
(3)
14.如图,∠1=38°,∠2=41°,∠3 =?
15.下面被小兔子遮住的角各是多少度?
参考答案:
1.58°
【分析】三角形的内角和是180°,直角是90°,用180°减去∠1度数再减去∠2度数即可算出∠3的度数。
【详解】∠3=180°-∠1-∠2
=180°-32°-90°
=148°-90°
=58°
2.120°
【分析】三角形的内角和等于180°,180°减35°,再减去25°等于∠3的度数,据此计算即可解答。
【详解】∠3=180°-35°-25°
=145°-25°
=120°
3.47米;52分米
【分析】是等腰梯形,把等腰梯形的四条边的长度相加即是梯形周长;是平行四边形,平行四边形对边平行且相等,先算出平行四边形一组邻边的和,再乘2即可。
【详解】17+11+8+11
=28+8+11
=36+11
=47(米)
(15+11)×2
=26×2
=52(分米)
4.40°;30°;80°
【分析】根据三角形的内角和为180°可知,分别用180°减去已知两个角的度数,求出各个图形中第三个角的度数。
【详解】180°-90°-50°=40°
180°-115°-35°-30°
180°-52°-48°=80°
5.∠1=70°
∠2=20°
∠3=60°
【分析】根据题图可知,∠3和120°的角组成一个平角,则∠3=180°-120°=60°。根据三角形的内角和为180°可知,∠1=180°-50°-∠3=70°。∠1、∠2和一个直角组成一个平角,则∠2=180°-90°-∠1=20°。
【详解】∠3=180°-120°=60°
∠1=180°-50°-∠3=180°-50°-60°=70°
∠2=180°-90°-∠1=180°-90°-70°=20°
6.∠B=150°;∠C=70°,∠A=40°;∠C=40°
【分析】(1)180°减两个已知角的度数即等于∠B的度数;
(2)等腰三角形的两个底角相等,所以∠C等于∠B,180°减∠C、∠B的度数等于∠A的度数;
(3)直角三角形两锐角和等于90°,90°减∠A等于∠C。
【详解】(1)∠B=180°-10°-20°
=170°-20°
=150°
(2)∠C=∠B=70°
∠A=180°-70°×2
=180°-140°
=40°
(3)∠C=90°-50°=40°
7.110°
【分析】先根据三角形的内角和等于180°求得三角形的另外一个角的度数,再用180°减去三角形的另外一个角的度数即等于∠1的度数。
【详解】180°-(50°+60°)
=180°-110°
=70°
180°-70°=110°
8.∠A=42°;∠D=115°
【分析】(1)∠ACB等于180°减80°,∠A等于180°减去∠B和∠ACB,据此即可解答;
(2)四边形内角和等于360°,用360°减90°,再减∠A和∠C,即等于∠D的度数,据此即可解答。
【详解】(1)∠ACB=180°-80°=100°
∠A=180°-∠B-∠ACB
=180°-38°-100°
=142°-100°
=42°
(2)∠D =360°-90°-∠A-∠C
=270°-40°-115°
=230°-115°
=115°
9.84°
【分析】三角形ABC是一个直角三角形,∠3=42°,可求出∠1=180°-90°-∠3,又因为,所以可求出∠2的度数。在三角形DBC中,用∠4=180°-∠1-∠2。
【详解】∠1=180°-90°-∠3
=180°-90°-42°
=90°-42°
=48°
∠4=180°-∠1-∠2
=180°-48°-48°
=132°-48°
=84°
10.(1)96°;(2)25°;(3)34°
【分析】三角形的内角和是180°,直角三角形中有一个角是直角等于90°,用180°减去三角形中已知两个角的度数,即可求出第三个角的度数。据此列式解答。
【详解】(1)180°-35°-49°
=145°-49°
=96°
(2)180°-90°-65°
=90°-65°
=25°
(3)180°-101°-45°
=79°-45°
=34°
11.30°;25°
【分析】三角形的内角和是180°。左边三角形中∠B是直角,∠B=90°,用180°-90°-60°即可求出∠A的度数;右边三角形中,用180°-135°-20°即可求出∠A的度数。
【详解】∠A=180°-90°-60°
=90°-60°
=30°
∠A=180°-135°-20°
=45°-20°
=25°
12.72°;32°;120°
【分析】三角形的内角和是180度,所以用180度,减去已知的两个角的度数,即可求出三角形的第三个角的度数,据此即可解答问题。
【详解】∠1=180°-62°-46°=72°
∠2=180°-58°-90°=32°
∠3=180°-35°-25°=120°
13.(1)22°
(2)38°
(3)95°
【分析】根据三角形的内角和是180°:(1)∠A=180°-130°-28°。(2)∠A=180°-52°-90°。(3)180°-135°=45°,∠A=180°-45°-40°。
【详解】(1)∠A=180°-130°-28°=22°
(2)∠A=180°-52°-90°=38°
(3)180°-135°=55°,∠A=180°-45°-40°=95°
14.79°
【分析】利用三角形内角和及图形中平角即可解决问题。
【详解】180°-38°-41°=101°
180°-101°=79°
答:∠3等于79°。
【点睛】本题主要考查学生的观察和分析问题的能力。
15.(1)40°(2)40°(3)35°
【分析】根据三角形内角和等于180度,已知两个角的度数,用180度减去两个角的度数,即是第三个角的度数,由此解答。
【详解】(1)180°-60°-80°
=120°-80°
=40°
(2)180°-115°-25°
=65°-25°
=40°
(3)180°-90°-55°
=90°-55°
=35°
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
第二单元《认识三角形和四边形》单元专项训练——图形计算题
1.算一算。
,是直角。求的度数。
2.求出∠3的度数。
3.图形计算(计算各图形的周长)。
4.算出下面各个未知角的度数。
5.求∠1、∠2、∠3的度数。
6.根据条件,求出三角形未知内角的度数。
7.算出下图中∠1的度数。
8.算出下面和的度数。
9.三角形ABC是一个直角三角形,三角形DBC是一个等腰三角形,,,求的度数。
10.计算下面各未知角的度数。
(1) (2)(3)
11.求下面各个三角形中∠A的度数。
12.求出下面各角的度数。
13.求∠A的度数。
(1)
(2)
(3)
14.如图,∠1=38°,∠2=41°,∠3 =?
15.下面被小兔子遮住的角各是多少度?
参考答案:
1.58°
【分析】三角形的内角和是180°,直角是90°,用180°减去∠1度数再减去∠2度数即可算出∠3的度数。
【详解】∠3=180°-∠1-∠2
=180°-32°-90°
=148°-90°
=58°
2.120°
【分析】三角形的内角和等于180°,180°减35°,再减去25°等于∠3的度数,据此计算即可解答。
【详解】∠3=180°-35°-25°
=145°-25°
=120°
3.47米;52分米
【分析】是等腰梯形,把等腰梯形的四条边的长度相加即是梯形周长;是平行四边形,平行四边形对边平行且相等,先算出平行四边形一组邻边的和,再乘2即可。
【详解】17+11+8+11
=28+8+11
=36+11
=47(米)
(15+11)×2
=26×2
=52(分米)
4.40°;30°;80°
【分析】根据三角形的内角和为180°可知,分别用180°减去已知两个角的度数,求出各个图形中第三个角的度数。
【详解】180°-90°-50°=40°
180°-115°-35°-30°
180°-52°-48°=80°
5.∠1=70°
∠2=20°
∠3=60°
【分析】根据题图可知,∠3和120°的角组成一个平角,则∠3=180°-120°=60°。根据三角形的内角和为180°可知,∠1=180°-50°-∠3=70°。∠1、∠2和一个直角组成一个平角,则∠2=180°-90°-∠1=20°。
【详解】∠3=180°-120°=60°
∠1=180°-50°-∠3=180°-50°-60°=70°
∠2=180°-90°-∠1=180°-90°-70°=20°
6.∠B=150°;∠C=70°,∠A=40°;∠C=40°
【分析】(1)180°减两个已知角的度数即等于∠B的度数;
(2)等腰三角形的两个底角相等,所以∠C等于∠B,180°减∠C、∠B的度数等于∠A的度数;
(3)直角三角形两锐角和等于90°,90°减∠A等于∠C。
【详解】(1)∠B=180°-10°-20°
=170°-20°
=150°
(2)∠C=∠B=70°
∠A=180°-70°×2
=180°-140°
=40°
(3)∠C=90°-50°=40°
7.110°
【分析】先根据三角形的内角和等于180°求得三角形的另外一个角的度数,再用180°减去三角形的另外一个角的度数即等于∠1的度数。
【详解】180°-(50°+60°)
=180°-110°
=70°
180°-70°=110°
8.∠A=42°;∠D=115°
【分析】(1)∠ACB等于180°减80°,∠A等于180°减去∠B和∠ACB,据此即可解答;
(2)四边形内角和等于360°,用360°减90°,再减∠A和∠C,即等于∠D的度数,据此即可解答。
【详解】(1)∠ACB=180°-80°=100°
∠A=180°-∠B-∠ACB
=180°-38°-100°
=142°-100°
=42°
(2)∠D =360°-90°-∠A-∠C
=270°-40°-115°
=230°-115°
=115°
9.84°
【分析】三角形ABC是一个直角三角形,∠3=42°,可求出∠1=180°-90°-∠3,又因为,所以可求出∠2的度数。在三角形DBC中,用∠4=180°-∠1-∠2。
【详解】∠1=180°-90°-∠3
=180°-90°-42°
=90°-42°
=48°
∠4=180°-∠1-∠2
=180°-48°-48°
=132°-48°
=84°
10.(1)96°;(2)25°;(3)34°
【分析】三角形的内角和是180°,直角三角形中有一个角是直角等于90°,用180°减去三角形中已知两个角的度数,即可求出第三个角的度数。据此列式解答。
【详解】(1)180°-35°-49°
=145°-49°
=96°
(2)180°-90°-65°
=90°-65°
=25°
(3)180°-101°-45°
=79°-45°
=34°
11.30°;25°
【分析】三角形的内角和是180°。左边三角形中∠B是直角,∠B=90°,用180°-90°-60°即可求出∠A的度数;右边三角形中,用180°-135°-20°即可求出∠A的度数。
【详解】∠A=180°-90°-60°
=90°-60°
=30°
∠A=180°-135°-20°
=45°-20°
=25°
12.72°;32°;120°
【分析】三角形的内角和是180度,所以用180度,减去已知的两个角的度数,即可求出三角形的第三个角的度数,据此即可解答问题。
【详解】∠1=180°-62°-46°=72°
∠2=180°-58°-90°=32°
∠3=180°-35°-25°=120°
13.(1)22°
(2)38°
(3)95°
【分析】根据三角形的内角和是180°:(1)∠A=180°-130°-28°。(2)∠A=180°-52°-90°。(3)180°-135°=45°,∠A=180°-45°-40°。
【详解】(1)∠A=180°-130°-28°=22°
(2)∠A=180°-52°-90°=38°
(3)180°-135°=55°,∠A=180°-45°-40°=95°
14.79°
【分析】利用三角形内角和及图形中平角即可解决问题。
【详解】180°-38°-41°=101°
180°-101°=79°
答:∠3等于79°。
【点睛】本题主要考查学生的观察和分析问题的能力。
15.(1)40°(2)40°(3)35°
【分析】根据三角形内角和等于180度,已知两个角的度数,用180度减去两个角的度数,即是第三个角的度数,由此解答。
【详解】(1)180°-60°-80°
=120°-80°
=40°
(2)180°-115°-25°
=65°-25°
=40°
(3)180°-90°-55°
=90°-55°
=35°
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
