第2单元认识三角形和四边形常考易错检测卷-数学四年级下册北师大版(含解析)
文档属性
| 名称 | 第2单元认识三角形和四边形常考易错检测卷-数学四年级下册北师大版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 423.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-16 20:24:13 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第2单元认识三角形和四边形常考易错检测卷-数学四年级下册北师大版
一、选择题
1.从长度分别为1cm、4cm、5cm和8cm的四根小棒中任意选择三根围成一个三角形,下面选择正确的是( )。
A.1cm、4cm、8cm B.4cm、5cm、8cm C.1cm、5cm、8cm
2.一个等腰三角形,一条边长10cm,另一条边长5cm,那么它的周长是( )cm。
A.25 B.20 C.20或25
3.如图,已知∠3+∠4=95°,则∠1=( )。
A.95° B.85° C.105°
4.下图中被遮住的图形一定不是( )。
A.梯形 B.平行四边形 C.三角形
5.一个等腰三角形被分成了如下图的两个三角形,下列说法正确的是( )。
A.①号面积和②号面积一样大 B.①号周长和②号周长一样大
C.①号内角和和②号内角和一样大
6.三角形的两条边长分别是4厘米和10厘米,第三条边可能是( )厘米。
A.4 B.10 C.14
二、填空题
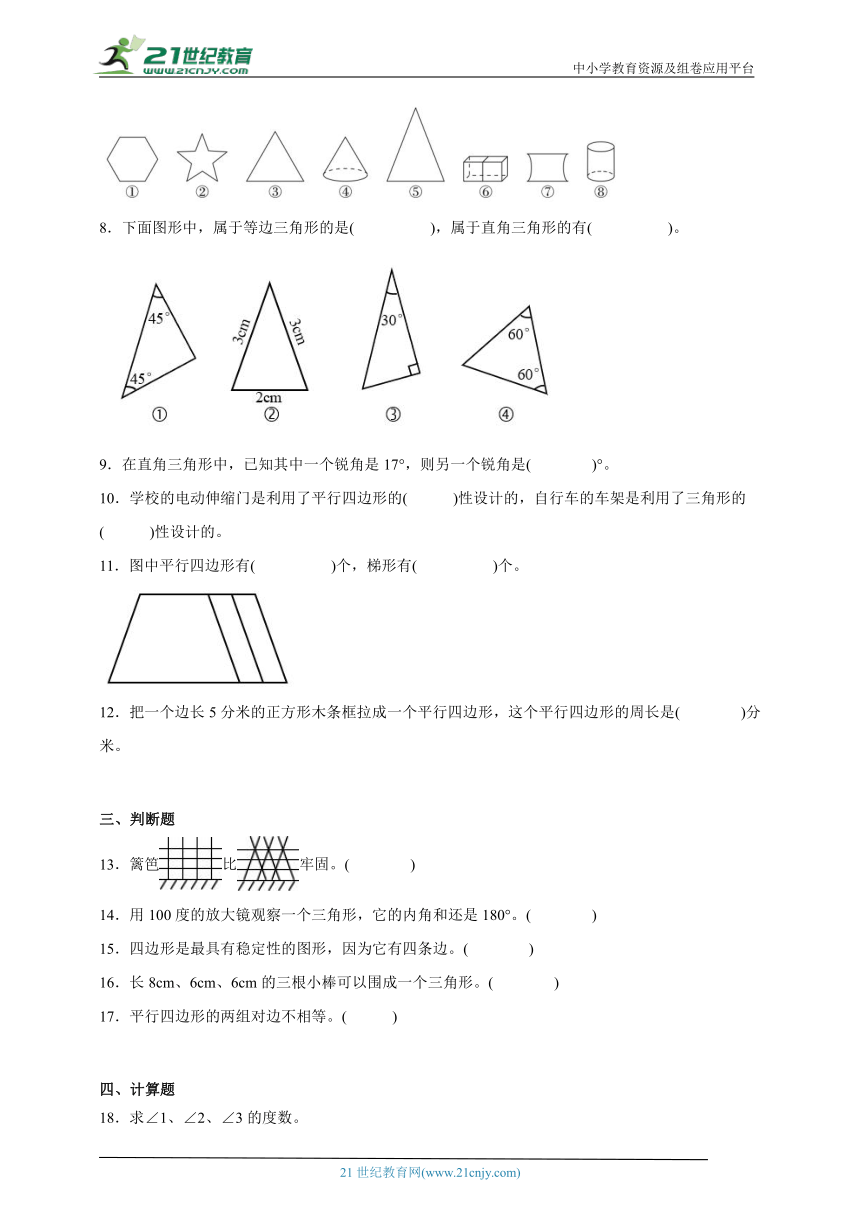
7.下面各图形中,( )是立体图形;( )是等腰三角形。(填序号)
8.下面图形中,属于等边三角形的是( ),属于直角三角形的有( )。
9.在直角三角形中,已知其中一个锐角是17°,则另一个锐角是( )°。
10.学校的电动伸缩门是利用了平行四边形的( )性设计的,自行车的车架是利用了三角形的( )性设计的。
11.图中平行四边形有( )个,梯形有( )个。
12.把一个边长5分米的正方形木条框拉成一个平行四边形,这个平行四边形的周长是( )分米。
三、判断题
13.篱笆比牢固。( )
14.用100度的放大镜观察一个三角形,它的内角和还是180°。( )
15.四边形是最具有稳定性的图形,因为它有四条边。( )
16.长8cm、6cm、6cm的三根小棒可以围成一个三角形。( )
17.平行四边形的两组对边不相等。( )
四、计算题
18.求∠1、∠2、∠3的度数。
五、解答题
19.下面是淘气测量的两块三角形花坛各边的长。(单位:m)
你认为淘气测量的结果正确吗?请说明理由。
20.学校举行风筝比赛,李东做了一个风筝,风筝的造型是等腰三角形。其中有一个角是48°,其它两个角各是多少度?
21.从右面五根小棒中任选三根围成一个等腰三角形。
(1)共有( )种选法。
(2)围成的等腰三角形的周长分别是多少厘米?
22.一根铁丝可以围成一个腰长12厘米,底长18厘米的等腰三角形,如果改围一个等边三角形,那么等边三角形的边长是多少厘米?
23.如图是一个等边三角形,已知∠1=∠2,∠3=∠4,求∠5的度数。
参考答案:
1.B
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【详解】A.4+1<8,不可以组成三角形;
B.4+5>8,能组成三角形;
C.1+5<8,不能组成三角形。
故答案为:B
【点睛】本题考查了三角形的三边关系的应用。
2.A
【分析】等腰三角形中,两条腰相等,则第三条边可能是10cm或者5cm。三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边。据此判断第三条边是10cm还是5cm,或者两种情况都符合,再将三条边的长度相加,求出三角形的周长。
【详解】5+5=10,则长5cm、5cm、10cm的三条线段不能围成一个三角形。
5+10>10,则长5cm、10cm、10cm的三条线段能围成一个三角形。第三条边长10cm。
5+10+10=25(cm)
那么它的周长是25cm。
故答案为:A
【点睛】本题考查等腰三角形的特征和三角形的三边关系,关键是根据三边关系明确第三条边的长度。
3.A
【分析】观察上图可知,∠2等于180°减去∠3、∠4的度数和,∠1等于180°减∠2,据此即可解答。
【详解】∠2=180°-(∠3+∠4)
=180°-95°
=85°
∠1=180°-∠2
=180°-85°
=95°
故答案为:A
【点睛】本题主要考查学生对三角形内角和知识的掌握和灵活运用。
4.B
【分析】两组对边分别平行的四边形是平行四边形,只有一组对边平行的四边形是梯形,同一平面内不在同一直线上的三条线段“首尾”顺次连接所组成的封闭图形是三角形,据此解答。
【详解】由图可知,被遮住的图形至少有一组对边不平行,所以它一定不是平行四边形。
故答案为:B
【点睛】本题考查了平行四边形的特征,熟练掌握所学图形的特征是解题关键。
5.C
【分析】周长:①号的周长=1条腰长+公共边+第三条边,②号的周长=1条腰长+公共边+第三条边;其中①号的第三条边大于②号的第三条边,则①号的周长>②号的周长;
面积:从图中可知,①号的面积>②号的面积;
三角形内角和:任意三角形的内角和都是180度。
【详解】A.①号的面积>②号的面积,原题说法错误;
B.①号的周长>②号的周长,原题说法错误;
C.①号内角和和②号内角和一样大,原题说法正确。
故答案为:C
【点睛】熟练掌握等腰三角形的特征以及三角形的内角和是180度是解答此题的关键。
6.B
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,求得第三边的取值范围,即可得出结果。
【详解】根据三角形的三边关系可得,第三边应大于10-4=6(厘米),而小于10+4=14(厘米);6<第三边<14,结合选项可知:第三条边可能是10厘米。
故答案为:B
【点睛】明确三角形的三边关系是解答此题的关键。
7. ④⑥⑧ ③⑤
【分析】立体图形是各个部分不在同一平面内的图形;平面图形所表示的各个部分都在同一平面内。三角形是由同一平面内不在同一直线上的三条线段“首尾”依次连接所组成的封闭图形,至少有两条边相等的三角形是等腰三角形。
【详解】上面各图形中,④⑥⑧是立体图形;③⑤是等腰三角形。
【点睛】本题主要考查图形的分类以及图形的认识,要熟练掌握图形的特征。
8. ④ ①③
【分析】三角形按边分可分为:等边三角形、等腰三角形、不等边三角形。两个底角相等或两条边相等的三角形是等腰三角形,三个角都相等或三条边都相等的三角形是等边三角形。
三角形按角分类可以分成:锐角三角形;直角三角形;钝角三角形。
1、锐角三角形:三个角都小于90°。
2、直角三角形:其中一个角等于90°。
3、钝角三角形:其中一个角一定大于90°小于180°。
【详解】第三个角的度数是:180°-45°-45°=90°,按角分,它是直角三角形,按边分,它是等腰三角形;
按角分,它是锐角三角形,按边分,它是等腰三角形;
有一个角是直角,按角分,它是直角三角形;
第三个角的度数是:180°-60°-60°=60°,按角分,它是锐角三角形,按边分,它是等边三角形;
属于等边三角形的是④,属于直角三角形的有①③。
【点睛】熟练掌握三角形的内角和定理以及三角形的分类是解答此题的关键。
9.73
【分析】因为三角形的内角和是180度,直角三角形中有一个角是直角,给出的直角三角形中一个锐角是17°,用内角和分别减去90°和17°,即可求出另一个锐角的度数。
【详解】180°-90°-17°
=90°-17°
=73°
在直角三角形中,已知其中一个锐角是17°,则另一个锐角是(73)°
【点睛】正确利用直角三角形的性质,明确三角形的内角和是180°,是解此题的关键。
10. 易变形 稳定
【分析】学校大门做成的伸缩门里面的一部分是平行四边形的造型,它是应用了平行四边形的不稳定性实现伸缩作用;自行车的车架是三角形形状,自行车的行驶稳定也是由于三角形的稳定性的特征。
【详解】学校的电动伸缩门是利用了平行四边形的易变形性设计的,自行车的车架是利用了三角形的稳定性设计的。
【点睛】此题考查了四边形和三角形的特征。
11. 3/三 3/三
【分析】两组对边分别平行的四边形,叫做平行四边形;只有一组对边平行的四边形叫做梯形;依此计算出平行四边形和梯形的个数即可。
【详解】2+1=3(个),即图中平行四边形有3个;
1+2=3(个),即梯形有3个。
【点睛】熟练掌握平行四边形和梯形的特点是解答此题的关键。
12.20
【分析】把正方形拉成平行四边形,四边形的四条边的长度不变,平行四边形的四条边的长度都还是5分米,5乘4即可求出周长。
【详解】5×4=20(分米),周长是20分米。
【点睛】四条边的长度之和即为这个平行四边形的周长。
13.×
【分析】三角形稳定性是指三角形具有稳定性,有着稳固、坚定、耐压的特点。平行四边形的不稳定性就是指平行四边形边长确定,其形状、大小不能完全确定。据此解答即可。
【详解】应用平行四边形的不稳定性,应用三角形稳定性。则更牢固。
故答案为:×。
【点睛】解答此题的关键是明确三角形的稳定性,生活中还有很多利用三角形稳定性的例子,比如三角形房架、矩形门框的斜拉条、起重机的三角形吊臂和高压输电线的铁塔等。
14.√
【分析】用100度的放大镜观察一个三角形,三角形的边长增大,但角的大小没变,因此三角形的内角和还是180°,据此即可解答。
【详解】根据分析可知,用100度的放大镜观察一个三角形,它的内角和还是180°,所以判断正确。
【点睛】本题主要考查学生对影响角的大小的因素的掌握和灵活运用。
15.×
【详解】四边形易变形,具有不稳定性;三角形具有稳定性,有着稳固、坚定、耐压的特点;所以判断错误。
16.√
【分析】根据三角形的特征:两边之和大于第三边,两边的差一定小于第三边,可据此进行判断。
【详解】6+6=12,12>8;8-6=2,2<6。所以长8cm、6cm、6cm的三根小棒可以围成一个三角形。
所以判断正确。
【点睛】本题主要考查对三角形三边之间关系的掌握和灵活运用。
17.×
【解析】略
18.∠1=70°
∠2=20°
∠3=60°
【分析】根据题图可知,∠3和120°的角组成一个平角,则∠3=180°-120°=60°。根据三角形的内角和为180°可知,∠1=180°-50°-∠3=70°。∠1、∠2和一个直角组成一个平角,则∠2=180°-90°-∠1=20°。
【详解】∠3=180°-120°=60°
∠1=180°-50°-∠3=180°-50°-60°=70°
∠2=180°-90°-∠1=180°-90°-70°=20°
19.不正确。理由见详解
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边。直角三角形中,斜边应大于两个直角边。
【详解】不正确。图1中,10+14<25,则长10米、14米和25米的三条线段不能组成一个三角形。图2是直角三角形花坛,斜边应比两条直角边都长,而现在斜边与其中一条直角边相等。所以淘气测量的结果不正确。
【点睛】本题考查三角形的三边关系,常利用这个关系判断给出的三条线段能否组成一个三角形。
20.66°,66°或48°,84°
【分析】(1)如果48°的角为顶角,则一个底角的度数等于180°减去顶角的度数差,再除以2;
(2)如果48°的角为底角,另一个底角也为48°,顶角度数等于180°减去两个底角的度数。
【详解】(1)48°的角为顶角:
(180°-48°)÷2
=132°÷2
=66°
(2)48°的角为底角:
180°-48°×2
=180°-96°
=84°
答:两个角都为66°,或者一个角为48°,另一个角为84°。
【点睛】48°的角可以顶角,也可以是底角,这是解答本题的关键。
21.(1)3
(2)10厘米、15厘米和16厘米
【分析】(1)如果选3厘米的小棒为腰,3+3=6,所以底只能是4厘米的小棒;如果选6厘米的小棒为腰,底可以是3厘米或4厘米的小棒;共有3种选法;
(2)根据(1)能围成三角形的三种选法,分别计算出围成的三角形的周长即可。
【详解】(1)共有3种选法。
(2)3+3+4
=6+4
=10(厘米)
6+6+3
=12+3
=15(厘米)
6+6+4
=12+4
=16(厘米)
答:围成的等腰三角形的周长分别是10厘米、15厘米和16厘米。
【点睛】本题主要考查学生对三角形三边间的关系和等腰三角形特点的掌握。
22.14厘米
【分析】等腰三角形的两条腰相等。则这个等腰三角形的周长为12+12+18厘米。用同样的铁丝围成等边三角形,则这个等边三角形的周长也是12+12+18厘米。等边三角形的三条边相等,则边长=周长÷3,据此解答即可。
【详解】(12+12+18)÷3
=42÷3
=14(厘米)
答:等边三角形的边长是14厘米。
【点睛】等腰三角形的周长=2×腰+底,等边三角形的周长=3×边长。
23.120°
【分析】等边三角形的三个角相等,根据三角形的内角和为180°可知,等边三角形的三个角均为180°÷3=60°。∠1=∠2,∠3=∠4,则∠1=∠2=∠3=∠4=60°÷2=30°。则∠5=180°-∠2-∠4。
【详解】180°÷3÷2=30°
180°-30°-30°=120°
则∠5=120°。
【点睛】熟练掌握三角形的内角和是解决本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第2单元认识三角形和四边形常考易错检测卷-数学四年级下册北师大版
一、选择题
1.从长度分别为1cm、4cm、5cm和8cm的四根小棒中任意选择三根围成一个三角形,下面选择正确的是( )。
A.1cm、4cm、8cm B.4cm、5cm、8cm C.1cm、5cm、8cm
2.一个等腰三角形,一条边长10cm,另一条边长5cm,那么它的周长是( )cm。
A.25 B.20 C.20或25
3.如图,已知∠3+∠4=95°,则∠1=( )。
A.95° B.85° C.105°
4.下图中被遮住的图形一定不是( )。
A.梯形 B.平行四边形 C.三角形
5.一个等腰三角形被分成了如下图的两个三角形,下列说法正确的是( )。
A.①号面积和②号面积一样大 B.①号周长和②号周长一样大
C.①号内角和和②号内角和一样大
6.三角形的两条边长分别是4厘米和10厘米,第三条边可能是( )厘米。
A.4 B.10 C.14
二、填空题
7.下面各图形中,( )是立体图形;( )是等腰三角形。(填序号)
8.下面图形中,属于等边三角形的是( ),属于直角三角形的有( )。
9.在直角三角形中,已知其中一个锐角是17°,则另一个锐角是( )°。
10.学校的电动伸缩门是利用了平行四边形的( )性设计的,自行车的车架是利用了三角形的( )性设计的。
11.图中平行四边形有( )个,梯形有( )个。
12.把一个边长5分米的正方形木条框拉成一个平行四边形,这个平行四边形的周长是( )分米。
三、判断题
13.篱笆比牢固。( )
14.用100度的放大镜观察一个三角形,它的内角和还是180°。( )
15.四边形是最具有稳定性的图形,因为它有四条边。( )
16.长8cm、6cm、6cm的三根小棒可以围成一个三角形。( )
17.平行四边形的两组对边不相等。( )
四、计算题
18.求∠1、∠2、∠3的度数。
五、解答题
19.下面是淘气测量的两块三角形花坛各边的长。(单位:m)
你认为淘气测量的结果正确吗?请说明理由。
20.学校举行风筝比赛,李东做了一个风筝,风筝的造型是等腰三角形。其中有一个角是48°,其它两个角各是多少度?
21.从右面五根小棒中任选三根围成一个等腰三角形。
(1)共有( )种选法。
(2)围成的等腰三角形的周长分别是多少厘米?
22.一根铁丝可以围成一个腰长12厘米,底长18厘米的等腰三角形,如果改围一个等边三角形,那么等边三角形的边长是多少厘米?
23.如图是一个等边三角形,已知∠1=∠2,∠3=∠4,求∠5的度数。
参考答案:
1.B
【分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【详解】A.4+1<8,不可以组成三角形;
B.4+5>8,能组成三角形;
C.1+5<8,不能组成三角形。
故答案为:B
【点睛】本题考查了三角形的三边关系的应用。
2.A
【分析】等腰三角形中,两条腰相等,则第三条边可能是10cm或者5cm。三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边。据此判断第三条边是10cm还是5cm,或者两种情况都符合,再将三条边的长度相加,求出三角形的周长。
【详解】5+5=10,则长5cm、5cm、10cm的三条线段不能围成一个三角形。
5+10>10,则长5cm、10cm、10cm的三条线段能围成一个三角形。第三条边长10cm。
5+10+10=25(cm)
那么它的周长是25cm。
故答案为:A
【点睛】本题考查等腰三角形的特征和三角形的三边关系,关键是根据三边关系明确第三条边的长度。
3.A
【分析】观察上图可知,∠2等于180°减去∠3、∠4的度数和,∠1等于180°减∠2,据此即可解答。
【详解】∠2=180°-(∠3+∠4)
=180°-95°
=85°
∠1=180°-∠2
=180°-85°
=95°
故答案为:A
【点睛】本题主要考查学生对三角形内角和知识的掌握和灵活运用。
4.B
【分析】两组对边分别平行的四边形是平行四边形,只有一组对边平行的四边形是梯形,同一平面内不在同一直线上的三条线段“首尾”顺次连接所组成的封闭图形是三角形,据此解答。
【详解】由图可知,被遮住的图形至少有一组对边不平行,所以它一定不是平行四边形。
故答案为:B
【点睛】本题考查了平行四边形的特征,熟练掌握所学图形的特征是解题关键。
5.C
【分析】周长:①号的周长=1条腰长+公共边+第三条边,②号的周长=1条腰长+公共边+第三条边;其中①号的第三条边大于②号的第三条边,则①号的周长>②号的周长;
面积:从图中可知,①号的面积>②号的面积;
三角形内角和:任意三角形的内角和都是180度。
【详解】A.①号的面积>②号的面积,原题说法错误;
B.①号的周长>②号的周长,原题说法错误;
C.①号内角和和②号内角和一样大,原题说法正确。
故答案为:C
【点睛】熟练掌握等腰三角形的特征以及三角形的内角和是180度是解答此题的关键。
6.B
【分析】根据三角形的三边关系“任意两边之和大于第三边,任意两边之差小于第三边”,求得第三边的取值范围,即可得出结果。
【详解】根据三角形的三边关系可得,第三边应大于10-4=6(厘米),而小于10+4=14(厘米);6<第三边<14,结合选项可知:第三条边可能是10厘米。
故答案为:B
【点睛】明确三角形的三边关系是解答此题的关键。
7. ④⑥⑧ ③⑤
【分析】立体图形是各个部分不在同一平面内的图形;平面图形所表示的各个部分都在同一平面内。三角形是由同一平面内不在同一直线上的三条线段“首尾”依次连接所组成的封闭图形,至少有两条边相等的三角形是等腰三角形。
【详解】上面各图形中,④⑥⑧是立体图形;③⑤是等腰三角形。
【点睛】本题主要考查图形的分类以及图形的认识,要熟练掌握图形的特征。
8. ④ ①③
【分析】三角形按边分可分为:等边三角形、等腰三角形、不等边三角形。两个底角相等或两条边相等的三角形是等腰三角形,三个角都相等或三条边都相等的三角形是等边三角形。
三角形按角分类可以分成:锐角三角形;直角三角形;钝角三角形。
1、锐角三角形:三个角都小于90°。
2、直角三角形:其中一个角等于90°。
3、钝角三角形:其中一个角一定大于90°小于180°。
【详解】第三个角的度数是:180°-45°-45°=90°,按角分,它是直角三角形,按边分,它是等腰三角形;
按角分,它是锐角三角形,按边分,它是等腰三角形;
有一个角是直角,按角分,它是直角三角形;
第三个角的度数是:180°-60°-60°=60°,按角分,它是锐角三角形,按边分,它是等边三角形;
属于等边三角形的是④,属于直角三角形的有①③。
【点睛】熟练掌握三角形的内角和定理以及三角形的分类是解答此题的关键。
9.73
【分析】因为三角形的内角和是180度,直角三角形中有一个角是直角,给出的直角三角形中一个锐角是17°,用内角和分别减去90°和17°,即可求出另一个锐角的度数。
【详解】180°-90°-17°
=90°-17°
=73°
在直角三角形中,已知其中一个锐角是17°,则另一个锐角是(73)°
【点睛】正确利用直角三角形的性质,明确三角形的内角和是180°,是解此题的关键。
10. 易变形 稳定
【分析】学校大门做成的伸缩门里面的一部分是平行四边形的造型,它是应用了平行四边形的不稳定性实现伸缩作用;自行车的车架是三角形形状,自行车的行驶稳定也是由于三角形的稳定性的特征。
【详解】学校的电动伸缩门是利用了平行四边形的易变形性设计的,自行车的车架是利用了三角形的稳定性设计的。
【点睛】此题考查了四边形和三角形的特征。
11. 3/三 3/三
【分析】两组对边分别平行的四边形,叫做平行四边形;只有一组对边平行的四边形叫做梯形;依此计算出平行四边形和梯形的个数即可。
【详解】2+1=3(个),即图中平行四边形有3个;
1+2=3(个),即梯形有3个。
【点睛】熟练掌握平行四边形和梯形的特点是解答此题的关键。
12.20
【分析】把正方形拉成平行四边形,四边形的四条边的长度不变,平行四边形的四条边的长度都还是5分米,5乘4即可求出周长。
【详解】5×4=20(分米),周长是20分米。
【点睛】四条边的长度之和即为这个平行四边形的周长。
13.×
【分析】三角形稳定性是指三角形具有稳定性,有着稳固、坚定、耐压的特点。平行四边形的不稳定性就是指平行四边形边长确定,其形状、大小不能完全确定。据此解答即可。
【详解】应用平行四边形的不稳定性,应用三角形稳定性。则更牢固。
故答案为:×。
【点睛】解答此题的关键是明确三角形的稳定性,生活中还有很多利用三角形稳定性的例子,比如三角形房架、矩形门框的斜拉条、起重机的三角形吊臂和高压输电线的铁塔等。
14.√
【分析】用100度的放大镜观察一个三角形,三角形的边长增大,但角的大小没变,因此三角形的内角和还是180°,据此即可解答。
【详解】根据分析可知,用100度的放大镜观察一个三角形,它的内角和还是180°,所以判断正确。
【点睛】本题主要考查学生对影响角的大小的因素的掌握和灵活运用。
15.×
【详解】四边形易变形,具有不稳定性;三角形具有稳定性,有着稳固、坚定、耐压的特点;所以判断错误。
16.√
【分析】根据三角形的特征:两边之和大于第三边,两边的差一定小于第三边,可据此进行判断。
【详解】6+6=12,12>8;8-6=2,2<6。所以长8cm、6cm、6cm的三根小棒可以围成一个三角形。
所以判断正确。
【点睛】本题主要考查对三角形三边之间关系的掌握和灵活运用。
17.×
【解析】略
18.∠1=70°
∠2=20°
∠3=60°
【分析】根据题图可知,∠3和120°的角组成一个平角,则∠3=180°-120°=60°。根据三角形的内角和为180°可知,∠1=180°-50°-∠3=70°。∠1、∠2和一个直角组成一个平角,则∠2=180°-90°-∠1=20°。
【详解】∠3=180°-120°=60°
∠1=180°-50°-∠3=180°-50°-60°=70°
∠2=180°-90°-∠1=180°-90°-70°=20°
19.不正确。理由见详解
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边。直角三角形中,斜边应大于两个直角边。
【详解】不正确。图1中,10+14<25,则长10米、14米和25米的三条线段不能组成一个三角形。图2是直角三角形花坛,斜边应比两条直角边都长,而现在斜边与其中一条直角边相等。所以淘气测量的结果不正确。
【点睛】本题考查三角形的三边关系,常利用这个关系判断给出的三条线段能否组成一个三角形。
20.66°,66°或48°,84°
【分析】(1)如果48°的角为顶角,则一个底角的度数等于180°减去顶角的度数差,再除以2;
(2)如果48°的角为底角,另一个底角也为48°,顶角度数等于180°减去两个底角的度数。
【详解】(1)48°的角为顶角:
(180°-48°)÷2
=132°÷2
=66°
(2)48°的角为底角:
180°-48°×2
=180°-96°
=84°
答:两个角都为66°,或者一个角为48°,另一个角为84°。
【点睛】48°的角可以顶角,也可以是底角,这是解答本题的关键。
21.(1)3
(2)10厘米、15厘米和16厘米
【分析】(1)如果选3厘米的小棒为腰,3+3=6,所以底只能是4厘米的小棒;如果选6厘米的小棒为腰,底可以是3厘米或4厘米的小棒;共有3种选法;
(2)根据(1)能围成三角形的三种选法,分别计算出围成的三角形的周长即可。
【详解】(1)共有3种选法。
(2)3+3+4
=6+4
=10(厘米)
6+6+3
=12+3
=15(厘米)
6+6+4
=12+4
=16(厘米)
答:围成的等腰三角形的周长分别是10厘米、15厘米和16厘米。
【点睛】本题主要考查学生对三角形三边间的关系和等腰三角形特点的掌握。
22.14厘米
【分析】等腰三角形的两条腰相等。则这个等腰三角形的周长为12+12+18厘米。用同样的铁丝围成等边三角形,则这个等边三角形的周长也是12+12+18厘米。等边三角形的三条边相等,则边长=周长÷3,据此解答即可。
【详解】(12+12+18)÷3
=42÷3
=14(厘米)
答:等边三角形的边长是14厘米。
【点睛】等腰三角形的周长=2×腰+底,等边三角形的周长=3×边长。
23.120°
【分析】等边三角形的三个角相等,根据三角形的内角和为180°可知,等边三角形的三个角均为180°÷3=60°。∠1=∠2,∠3=∠4,则∠1=∠2=∠3=∠4=60°÷2=30°。则∠5=180°-∠2-∠4。
【详解】180°÷3÷2=30°
180°-30°-30°=120°
则∠5=120°。
【点睛】熟练掌握三角形的内角和是解决本题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
