广东省深圳市南山实验教育集团2023-2024学年九年级第一次学业质量检测数学试题(PDF版无答案)
文档属性
| 名称 | 广东省深圳市南山实验教育集团2023-2024学年九年级第一次学业质量检测数学试题(PDF版无答案) |  | |
| 格式 | |||
| 文件大小 | 707.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-03-30 22:33:43 | ||
图片预览

文档简介
深圳市南山实验教育集团 2023-2024 学年初三年级
第一次学业质量监测
数 学
说明: 1. 答题前,请将姓名、准考证号和学校用黑色字迹的钢笔或签字笔填写在
答题卡指定的位置上,并将条形码粘贴好。
2. 全卷共 6 页,共 22 题。考试时间 90 分钟,满分 100 分。
3. 作答选择题时,选出每题答案后,用 2B 铅笔把答题卡上对应题目答案
标号的信息点框涂黑。如需改动,用橡皮擦干净后,再选涂其它答案。
作答非选择题时,用黑色字迹的钢笔或签字笔将答案(含作辅助线)写
在答题卡指定区域内。写在本试卷或草稿纸上,其答案一律无效。
4. 考试结束后,请将答题卡交回。
第一部分 选择题
一、选择题(本大题共 10 小题,每小题 3 分,共 30 分,每小题有四个选项,其中
只有一个是正确的)
1. 笔、墨、纸、砚是中华民族传统的“文房四宝”,是中国书法的必备用具.如图
是一方寓意“规矩方圆”的砚台,它的俯视图是( )
A. B.
C. D.
(第 1 题图)
2. 下列运算结果中正确的是( ) -2
A. a2 = a B. (-2a2)3 = - 6a6 C. a2 a3 = a6 D. a5÷a3+a2=2a2
3. 已知 m 是方程 x2- x-1= 0 的一个根,则代数式 m2 - m 的值等于( )
A. -1 B. 0 C. 1 D. 2
4. 估算 6 15+1的结果( )
A. 在 6 和 7 之间 B. 在 7 和 8 之间
C. 在 8 和 9 之间 D. 在 9 和 10 之间
深圳市南山实验教育集团2023-2024学年初三年级第一次学业质量监测数学 数学 第1页,共6页
{#{QQABKQAQggAoAIJAARhCAQHSCACQkAGACAoOxAAIoAAACRFABAA=}#}
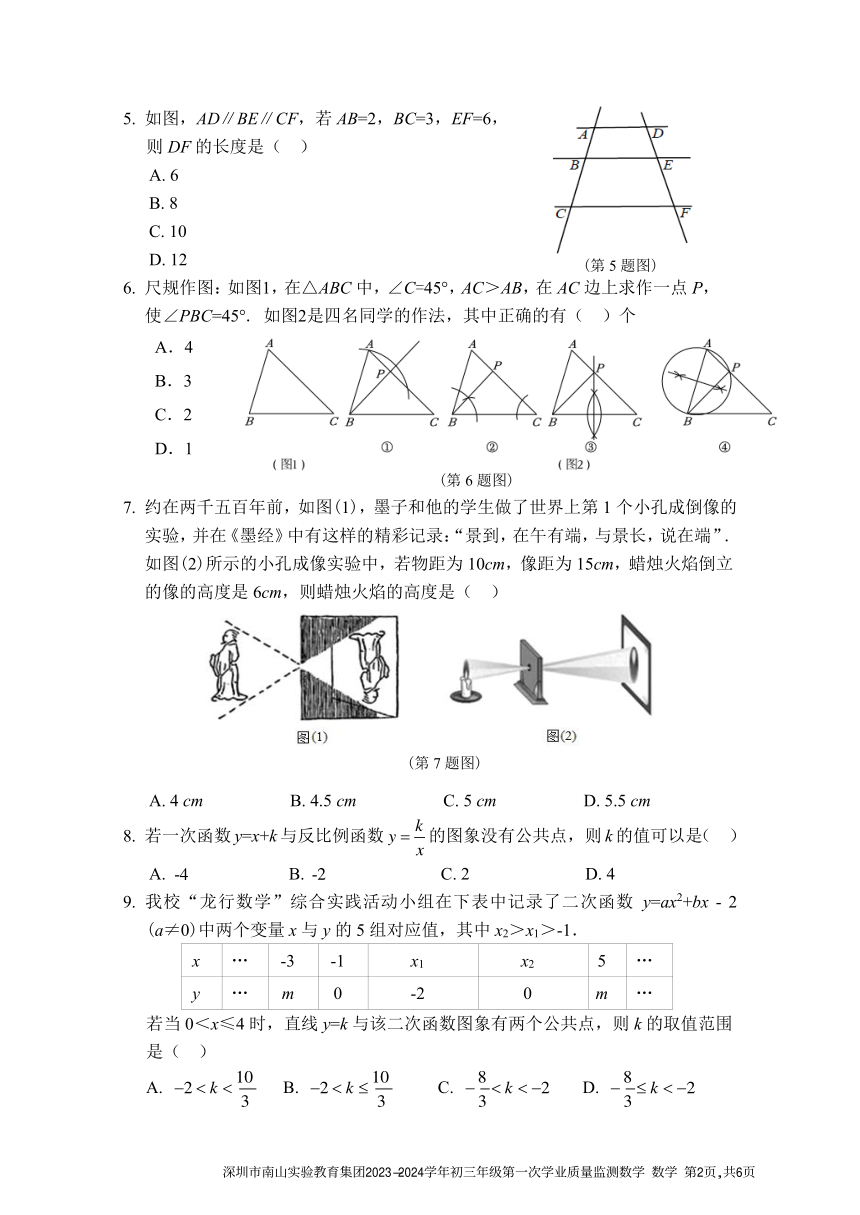
5. 如图,AD∥BE∥CF,若 AB=2,BC=3,EF=6,
则 DF 的长度是( )
A. 6
B. 8
C. 10
D. 12 (第 5 题图)
6. 尺规作图:如图1,在△ABC 中,∠C=45°,AC>AB,在 AC 边上求作一点 P,
使∠PBC=45°. 如图2是四名同学的作法,其中正确的有( ) 个
A.4
B.3
C.2
D.1
(第 6 题图)
7. 约在两千五百年前,如图(1),墨子和他的学生做了世界上第 1 个小孔成倒像的
实验,并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.
如图(2)所示的小孔成像实验中,若物距为 10cm,像距为 15cm,蜡烛火焰倒立
的像的高度是 6cm,则蜡烛火焰的高度是( )
(第 7 题图)
A. 4 cm B. 4.5 cm C. 5 cm D. 5.5 cm
k
8. 若一次函数 y=x+k与反比例函数 y = 的图象没有公共点, 则 k的值可以是( )
x
A. -4 B. -2 C. 2 D. 4
9. 我校“龙行数学”综合实践活动小组在下表中记录了二次函数 y=ax2+bx - 2
(a≠0)中两个变量 x 与 y 的 5 组对应值,其中 x2>x1>-1.
x … -3 -1 x1 x2 5 …
y … m 0 -2 0 m …
若当 0<x≤4 时,直线 y=k 与该二次函数图象有两个公共点,则 k 的取值范围
是( )
10 10 8 8
A. 2 k B. 2 k C. k 2 D. k 2
3 3 3 3
深圳市南山实验教育集团2023-2024学年初三年级第一次学业质量监测数学 数学 第2页,共6页
{#{QQABKQAQggAoAIJAARhCAQHSCACQkAGACAoOxAAIoAAACRFABAA=}#}
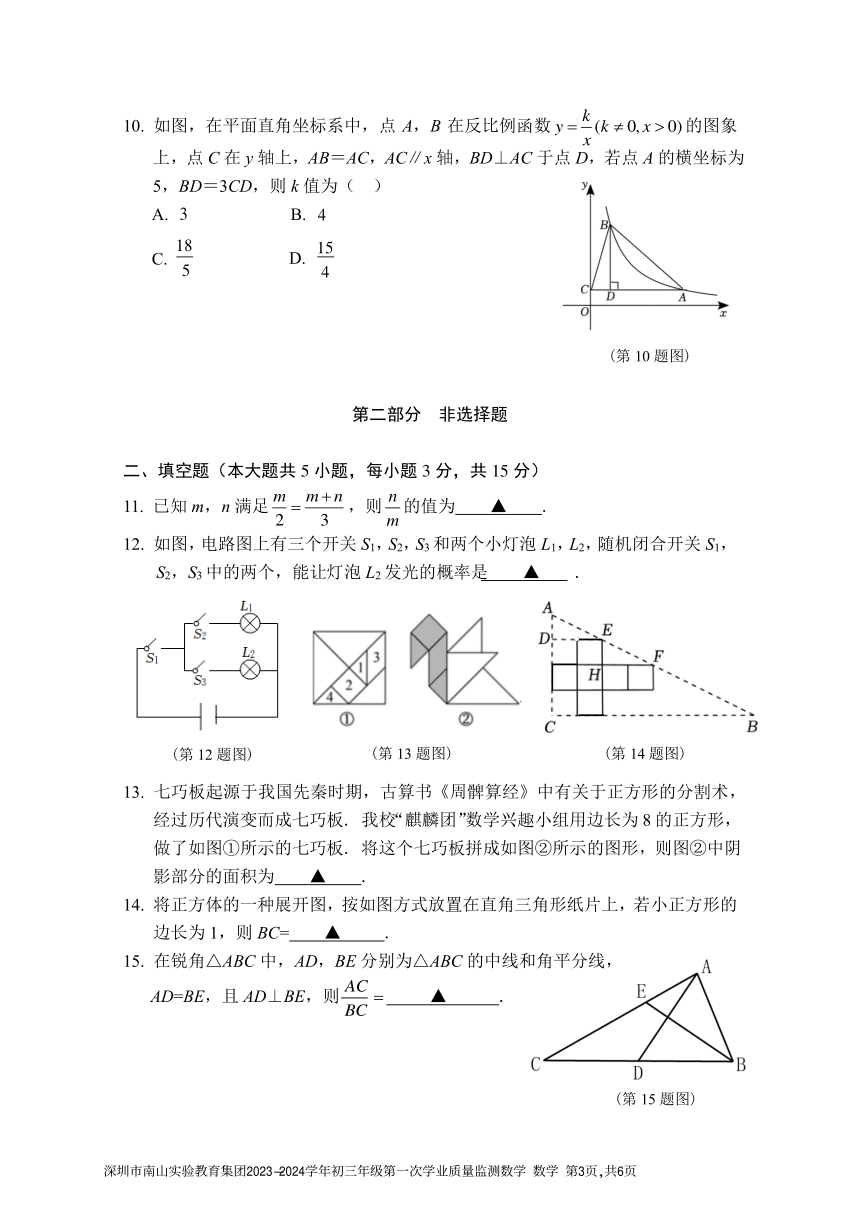
k
10. 如图,在平面直角坐标系中,点 A,B 在反比例函数 y = (k 0, x 0)的图象
x
上,点 C 在 y 轴上,AB=AC,AC∥x 轴,BD⊥AC 于点 D,若点 A 的横坐标为
5,BD=3CD,则 k 值为( )
A. 3 B. 4
18 15
C. D.
5 4
(第 10 题图)
第二部分 非选择题
二、填空题(本大题共 5 小题,每小题 3 分,共 15 分)
m m+ n n
11. 已知 m,n 满足 = ,则 的值为 ▲ .
2 3 m
12. 如图,电路图上有三个开关 S1,S2,S3 和两个小灯泡 L1,L2,随机闭合开关 S1,
S2,S3 中的两个,能让灯泡 L2 发光的概率是 ▲ .
(第 12 题图) (第 13 题图) (第 14 题图)
13. 七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,
经过历代演变而成七巧板. 我校“麒麟团”数学兴趣小组用边长为 8 的正方形,
做了如图①所示的七巧板. 将这个七巧板拼成如图②所示的图形,则图②中阴
影部分的面积为 ▲ .
14. 将正方体的一种展开图,按如图方式放置在直角三角形纸片上,若小正方形的
边长为 1,则 BC= ▲ .
15. 在锐角△ABC 中,AD,BE 分别为△ABC 的中线和角平分线,
AC
AD=BE,且 AD⊥BE,则 = ▲ .
BC
(第 15 题图)
深圳市南山实验教育集团2023-2024学年初三年级第一次学业质量监测数学 数学 第3页,共6页
{#{QQABKQAQggAoAIJAARhCAQHSCACQkAGACAoOxAAIoAAACRFABAA=}#}
三、解答题(本大题共 7 小题,共 55 分)
1 0
16. (本题 6 分)计算:( ) 1 (2023+ ) + | tan60 2 |
2
x 1 x2
3 17. (本题 6 分)先化简,再求值:( -1) ,其中 x=2024.
x2 + x x2 + 2x +1
18 15
18. (本题 8 分)开学初,为评估九年级学生的数学学情,并采取有针对性的教与
5 4
学,以在中考取得佳绩,我校抽取了九下部分学生的适应性考试数学成绩作为
样本分析,绘制成了如下两幅不完整的统计图,请根据图中提供的信息解答下
列问题:
差
16% 优
中 20%
n 良
44%
m
(1)这次调查中,一共抽取了多少名学生?
(2)求样本中成绩类别为“中”的人数,并将条形统计图补充完整;
(3)若我校九年级共有 1800 人参加了这次考试,请你估计该校九年级共有多
少名学生的数学成绩达到优秀?
19. (本题 8 分)如图,⊙O 是△ABC 的外接圆,AD 是⊙O 的直径,F 是 AD 延
长线上一点,连接 CD,CF,且∠DCF=∠CAD.
(1)求证:CF 是⊙O 的切线;
3
(2)若直径 AD=10, cos B = ,求 FD 的长.
5
深圳市南山实验教育集团2023-2024学年初三年级第一次学业质量监测数学 数学 第4页,共6页
{#{QQABKQAQggAoAIJAARhCAQHSCACQkAGACAoOxAAIoAAACRFABAA=}#}
20. (本题 8 分)“道路千万条,安全第一条”. 公安交警部门提醒市民,骑行必
须严格遵守“一盔一带”的法规. 某安全头盔经销商统计了某品牌头盔 1 月份
到 3 月份的销量,该品牌头盔 1 月份销售 500 个,3 月份销售 720 个,且从 1
月份到 3 月份销售量的月增长率相同.
(1)求该品牌头盔销售量的月增长率;
(2)若此种头盔的进价为 30 元/个,测算在市场中,当售价为 40 元/个时,月
销售量为 600 个,若在此基础上售价每上涨 1 元/个,则月销售量将减少
10 个,为使月销售利润达到 10000 元,并且尽可能让市民得到实惠,则
该品牌头盔的实际售价应定为多少元/个?
21. (本题 9 分)综合与应用
为促进中学生全面发展,培养良好体质,某班同学在“大课间”开展“集体跳
绳”运动. 跳绳时,绳甩到最高处时的形状是抛物线 y = ax2 +bx + c的部分图象.
以点 O 为原点建立如图所示的平面直角坐标系,若摇绳的两人之间间距为 6 米,
9
摇绳时两人手离地面均为 米;已知小丽身高 1.575 米,在距离摇绳者 A 的水
10
平距离 1.5 米处,绳子刚好经过她的头顶.
【阅读理解】
(1)求图中抛物线的解析式;(不需要求自变量取值范围)
【问题解决】
(2)体育龙老师身高 1.82 米,请问他适合参加本次运动吗?说明理由;
(3)若多人进入跳绳区齐跳,且大家身高均为 1.7 米,要求相邻两人之间间距
至少为 0.6 米,试计算最多可供几人齐跳.
深圳市南山实验教育集团2023-2024学年初三年级第一次学业质量监测数学 数学 第5页,共6页
{#{QQABKQAQggAoAIJAARhCAQHSCACQkAGACAoOxAAIoAAACRFABAA=}#}
22. (本题 10 分)综合与探究
【问题背景】北师大版数学八年级下册 P89 第 12 题(以下图片框内).
9
10 【初步探究】
(1)我们需利用图形的旋转与图形全等的联系,并把特殊角度一般化.如图 1,
在△ABC 与△ADE 中,AB=AC,AD=AE,∠BAC=∠DAE.求证:BD=CE.
【类比探究】
(2)如图 2,在边长为 3 的正方形 ABCD 中,点 E,F 分别是 CD,BC 上的点,
且 DE=1. 连接 AE,AF,EF,若∠EAF=45°,请直接写出 BF 的长.
【深入探究】
(3)如图 3,D,P 是等边△ABC 外两点,连接 BD 并取 BD 的中点 M,且
∠APD=120°,∠MPC=60°. 试猜想 PA 与 PD 的数量关系,并证明你的
结论.
【拓展应用】
(4)如图 4,在四边形 ABCD 中,∠ABC=60°,∠ADC=90°,AD=CD,
AB= 2 3,BD= 62 ,请直接写出 BC 的长.
深圳市南山实验教育集团2023-2024学年初三年级第一次学业质量监测数学 数学 第6页,共6页
{#{QQABKQAQggAoAIJAARhCAQHSCACQkAGACAoOxAAIoAAACRFABAA=}#}
第一次学业质量监测
数 学
说明: 1. 答题前,请将姓名、准考证号和学校用黑色字迹的钢笔或签字笔填写在
答题卡指定的位置上,并将条形码粘贴好。
2. 全卷共 6 页,共 22 题。考试时间 90 分钟,满分 100 分。
3. 作答选择题时,选出每题答案后,用 2B 铅笔把答题卡上对应题目答案
标号的信息点框涂黑。如需改动,用橡皮擦干净后,再选涂其它答案。
作答非选择题时,用黑色字迹的钢笔或签字笔将答案(含作辅助线)写
在答题卡指定区域内。写在本试卷或草稿纸上,其答案一律无效。
4. 考试结束后,请将答题卡交回。
第一部分 选择题
一、选择题(本大题共 10 小题,每小题 3 分,共 30 分,每小题有四个选项,其中
只有一个是正确的)
1. 笔、墨、纸、砚是中华民族传统的“文房四宝”,是中国书法的必备用具.如图
是一方寓意“规矩方圆”的砚台,它的俯视图是( )
A. B.
C. D.
(第 1 题图)
2. 下列运算结果中正确的是( ) -2
A. a2 = a B. (-2a2)3 = - 6a6 C. a2 a3 = a6 D. a5÷a3+a2=2a2
3. 已知 m 是方程 x2- x-1= 0 的一个根,则代数式 m2 - m 的值等于( )
A. -1 B. 0 C. 1 D. 2
4. 估算 6 15+1的结果( )
A. 在 6 和 7 之间 B. 在 7 和 8 之间
C. 在 8 和 9 之间 D. 在 9 和 10 之间
深圳市南山实验教育集团2023-2024学年初三年级第一次学业质量监测数学 数学 第1页,共6页
{#{QQABKQAQggAoAIJAARhCAQHSCACQkAGACAoOxAAIoAAACRFABAA=}#}
5. 如图,AD∥BE∥CF,若 AB=2,BC=3,EF=6,
则 DF 的长度是( )
A. 6
B. 8
C. 10
D. 12 (第 5 题图)
6. 尺规作图:如图1,在△ABC 中,∠C=45°,AC>AB,在 AC 边上求作一点 P,
使∠PBC=45°. 如图2是四名同学的作法,其中正确的有( ) 个
A.4
B.3
C.2
D.1
(第 6 题图)
7. 约在两千五百年前,如图(1),墨子和他的学生做了世界上第 1 个小孔成倒像的
实验,并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.
如图(2)所示的小孔成像实验中,若物距为 10cm,像距为 15cm,蜡烛火焰倒立
的像的高度是 6cm,则蜡烛火焰的高度是( )
(第 7 题图)
A. 4 cm B. 4.5 cm C. 5 cm D. 5.5 cm
k
8. 若一次函数 y=x+k与反比例函数 y = 的图象没有公共点, 则 k的值可以是( )
x
A. -4 B. -2 C. 2 D. 4
9. 我校“龙行数学”综合实践活动小组在下表中记录了二次函数 y=ax2+bx - 2
(a≠0)中两个变量 x 与 y 的 5 组对应值,其中 x2>x1>-1.
x … -3 -1 x1 x2 5 …
y … m 0 -2 0 m …
若当 0<x≤4 时,直线 y=k 与该二次函数图象有两个公共点,则 k 的取值范围
是( )
10 10 8 8
A. 2 k B. 2 k C. k 2 D. k 2
3 3 3 3
深圳市南山实验教育集团2023-2024学年初三年级第一次学业质量监测数学 数学 第2页,共6页
{#{QQABKQAQggAoAIJAARhCAQHSCACQkAGACAoOxAAIoAAACRFABAA=}#}
k
10. 如图,在平面直角坐标系中,点 A,B 在反比例函数 y = (k 0, x 0)的图象
x
上,点 C 在 y 轴上,AB=AC,AC∥x 轴,BD⊥AC 于点 D,若点 A 的横坐标为
5,BD=3CD,则 k 值为( )
A. 3 B. 4
18 15
C. D.
5 4
(第 10 题图)
第二部分 非选择题
二、填空题(本大题共 5 小题,每小题 3 分,共 15 分)
m m+ n n
11. 已知 m,n 满足 = ,则 的值为 ▲ .
2 3 m
12. 如图,电路图上有三个开关 S1,S2,S3 和两个小灯泡 L1,L2,随机闭合开关 S1,
S2,S3 中的两个,能让灯泡 L2 发光的概率是 ▲ .
(第 12 题图) (第 13 题图) (第 14 题图)
13. 七巧板起源于我国先秦时期,古算书《周髀算经》中有关于正方形的分割术,
经过历代演变而成七巧板. 我校“麒麟团”数学兴趣小组用边长为 8 的正方形,
做了如图①所示的七巧板. 将这个七巧板拼成如图②所示的图形,则图②中阴
影部分的面积为 ▲ .
14. 将正方体的一种展开图,按如图方式放置在直角三角形纸片上,若小正方形的
边长为 1,则 BC= ▲ .
15. 在锐角△ABC 中,AD,BE 分别为△ABC 的中线和角平分线,
AC
AD=BE,且 AD⊥BE,则 = ▲ .
BC
(第 15 题图)
深圳市南山实验教育集团2023-2024学年初三年级第一次学业质量监测数学 数学 第3页,共6页
{#{QQABKQAQggAoAIJAARhCAQHSCACQkAGACAoOxAAIoAAACRFABAA=}#}
三、解答题(本大题共 7 小题,共 55 分)
1 0
16. (本题 6 分)计算:( ) 1 (2023+ ) + | tan60 2 |
2
x 1 x2
3 17. (本题 6 分)先化简,再求值:( -1) ,其中 x=2024.
x2 + x x2 + 2x +1
18 15
18. (本题 8 分)开学初,为评估九年级学生的数学学情,并采取有针对性的教与
5 4
学,以在中考取得佳绩,我校抽取了九下部分学生的适应性考试数学成绩作为
样本分析,绘制成了如下两幅不完整的统计图,请根据图中提供的信息解答下
列问题:
差
16% 优
中 20%
n 良
44%
m
(1)这次调查中,一共抽取了多少名学生?
(2)求样本中成绩类别为“中”的人数,并将条形统计图补充完整;
(3)若我校九年级共有 1800 人参加了这次考试,请你估计该校九年级共有多
少名学生的数学成绩达到优秀?
19. (本题 8 分)如图,⊙O 是△ABC 的外接圆,AD 是⊙O 的直径,F 是 AD 延
长线上一点,连接 CD,CF,且∠DCF=∠CAD.
(1)求证:CF 是⊙O 的切线;
3
(2)若直径 AD=10, cos B = ,求 FD 的长.
5
深圳市南山实验教育集团2023-2024学年初三年级第一次学业质量监测数学 数学 第4页,共6页
{#{QQABKQAQggAoAIJAARhCAQHSCACQkAGACAoOxAAIoAAACRFABAA=}#}
20. (本题 8 分)“道路千万条,安全第一条”. 公安交警部门提醒市民,骑行必
须严格遵守“一盔一带”的法规. 某安全头盔经销商统计了某品牌头盔 1 月份
到 3 月份的销量,该品牌头盔 1 月份销售 500 个,3 月份销售 720 个,且从 1
月份到 3 月份销售量的月增长率相同.
(1)求该品牌头盔销售量的月增长率;
(2)若此种头盔的进价为 30 元/个,测算在市场中,当售价为 40 元/个时,月
销售量为 600 个,若在此基础上售价每上涨 1 元/个,则月销售量将减少
10 个,为使月销售利润达到 10000 元,并且尽可能让市民得到实惠,则
该品牌头盔的实际售价应定为多少元/个?
21. (本题 9 分)综合与应用
为促进中学生全面发展,培养良好体质,某班同学在“大课间”开展“集体跳
绳”运动. 跳绳时,绳甩到最高处时的形状是抛物线 y = ax2 +bx + c的部分图象.
以点 O 为原点建立如图所示的平面直角坐标系,若摇绳的两人之间间距为 6 米,
9
摇绳时两人手离地面均为 米;已知小丽身高 1.575 米,在距离摇绳者 A 的水
10
平距离 1.5 米处,绳子刚好经过她的头顶.
【阅读理解】
(1)求图中抛物线的解析式;(不需要求自变量取值范围)
【问题解决】
(2)体育龙老师身高 1.82 米,请问他适合参加本次运动吗?说明理由;
(3)若多人进入跳绳区齐跳,且大家身高均为 1.7 米,要求相邻两人之间间距
至少为 0.6 米,试计算最多可供几人齐跳.
深圳市南山实验教育集团2023-2024学年初三年级第一次学业质量监测数学 数学 第5页,共6页
{#{QQABKQAQggAoAIJAARhCAQHSCACQkAGACAoOxAAIoAAACRFABAA=}#}
22. (本题 10 分)综合与探究
【问题背景】北师大版数学八年级下册 P89 第 12 题(以下图片框内).
9
10 【初步探究】
(1)我们需利用图形的旋转与图形全等的联系,并把特殊角度一般化.如图 1,
在△ABC 与△ADE 中,AB=AC,AD=AE,∠BAC=∠DAE.求证:BD=CE.
【类比探究】
(2)如图 2,在边长为 3 的正方形 ABCD 中,点 E,F 分别是 CD,BC 上的点,
且 DE=1. 连接 AE,AF,EF,若∠EAF=45°,请直接写出 BF 的长.
【深入探究】
(3)如图 3,D,P 是等边△ABC 外两点,连接 BD 并取 BD 的中点 M,且
∠APD=120°,∠MPC=60°. 试猜想 PA 与 PD 的数量关系,并证明你的
结论.
【拓展应用】
(4)如图 4,在四边形 ABCD 中,∠ABC=60°,∠ADC=90°,AD=CD,
AB= 2 3,BD= 62 ,请直接写出 BC 的长.
深圳市南山实验教育集团2023-2024学年初三年级第一次学业质量监测数学 数学 第6页,共6页
{#{QQABKQAQggAoAIJAARhCAQHSCACQkAGACAoOxAAIoAAACRFABAA=}#}
同课章节目录
