北师大版九年级下册总复习摸底测试数学卷(含答案)
文档属性
| 名称 | 北师大版九年级下册总复习摸底测试数学卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 809.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-04-05 11:12:27 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
九年级数学总复习摸底测试卷(含参考答案)
满分:120分 考试时间:90分钟
一、选择题(本大题共10个小题,每题3分,满分30分)
1.在1,﹣2,0,这四个数中,最大的数是( )
A.1 B.﹣2 C.0 D.
2.如图,是由棱长都相等的四个小正方体组成的几何体.该几何体的左视图是( )
A. B. C. D.
3.下列运算正确的是( )
A.x2+2x2=3x4 B.(x3)4=x7
C.(2x+y)(2x﹣y)=2x2﹣y2 D.x÷x3=x﹣2
4.如图,AB为⊙O的切线,切点为B,连接OB、OA,交⊙O于点C,点D为优弧BC上一点,连接DC、DB,若∠A=20°,则∠D的大小为( )
A.20° B.35° C.25° D.15°
第4题图 第5题图
5.如图,边长为5的菱形ABCD对角线AC,BD交于点O,E是AB的中点,则EO的长为( )
A.10 B.5 C. D.
6.下面a,b的取值,能够说明命题“若a>b,则|a|>|b|”是假命题的是( )
A.a=3,b=2 B.a=3,b=﹣2 C.a=﹣3,b=﹣5 D.a=﹣3,b=5
7.若关于x的一元二次方程x2﹣2mx+m2﹣4m﹣1=0有两个实数根x1,x2,且(x1+2)(x2+2)﹣2x1x2=17,则m=( )
A.2或6 B.2或8 C.2 D.6
8.我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为x株,则符合题意的方程是( )
A.3(x﹣1)= B.=3 C.3x﹣1= D.=3
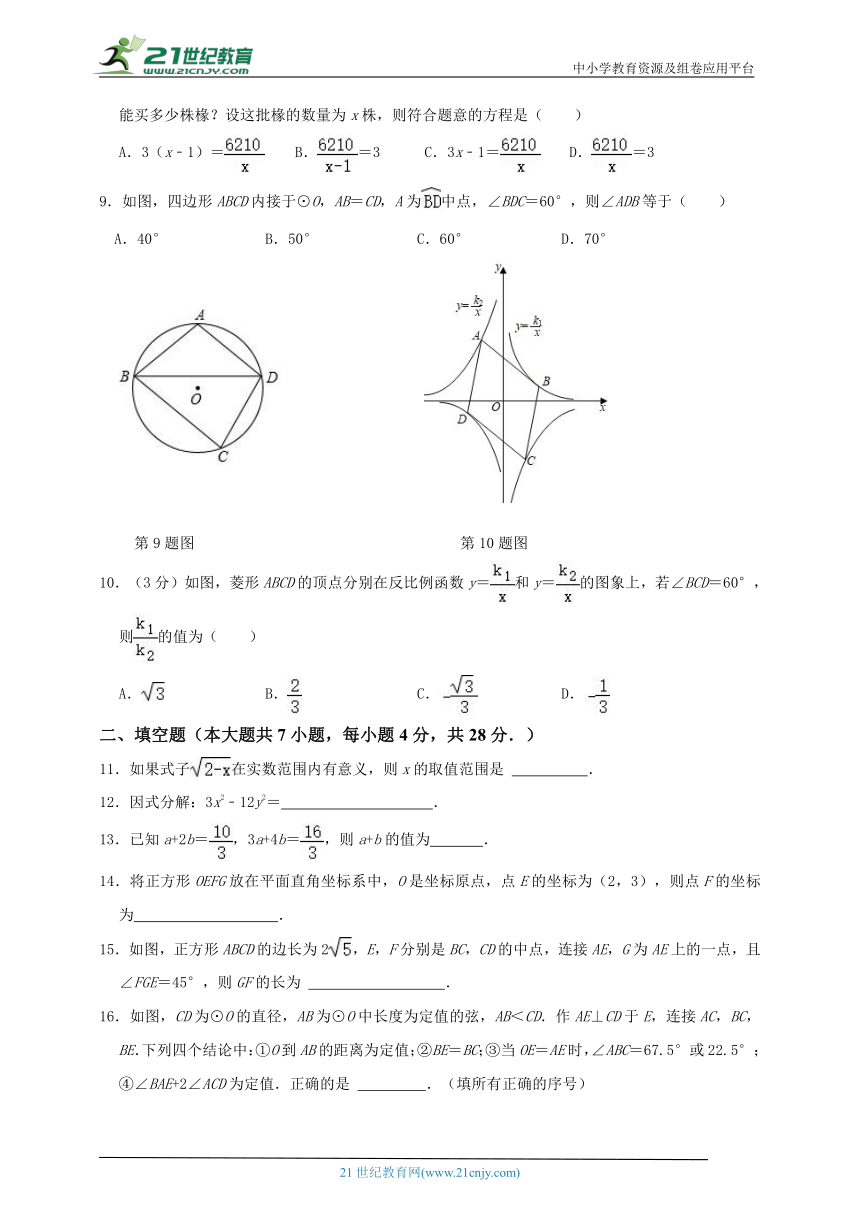
9.如图,四边形ABCD内接于⊙O,AB=CD,A为中点,∠BDC=60°,则∠ADB等于( )
A.40° B.50° C.60° D.70°
第9题图 第10题图
10.(3分)如图,菱形ABCD的顶点分别在反比例函数y=和y=的图象上,若∠BCD=60°,则的值为( )
A. B. C. D.
二、填空题(本大题共7小题,每小题4分,共28分.)
11.如果式子在实数范围内有意义,则x的取值范围是 .
12.因式分解:3x2﹣12y2= .
13.已知a+2b=,3a+4b=,则a+b的值为 .
14.将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点F的坐标为 .
15.如图,正方形ABCD的边长为2,E,F分别是BC,CD的中点,连接AE,G为AE上的一点,且∠FGE=45°,则GF的长为 .
16.如图,CD为⊙O的直径,AB为⊙O中长度为定值的弦,AB<CD.作AE⊥CD于E,连接AC,BC,BE.下列四个结论中:①O到AB的距离为定值;②BE=BC;③当OE=AE时,∠ABC=67.5°或22.5°;④∠BAE+2∠ACD为定值.正确的是 .(填所有正确的序号)
第15题图 第16题图 第17题图
17.两个反比例函数和在第一象限内的图象如图所示,点P在的图象上,PC⊥x轴于点C,交的图象于点A,PD⊥y轴于点D,交的图象于点B,当点P在的图象上运动时,以下结论:
①△ODB与△OCA的面积相等;
②四边形PAOB的面积不会发生变化;
③PA与PB始终相等;
④2<k<4.
其中一定正确的是 .
三.解答题(共3小题,每小题6分,共18分)
18.解方程组:.
19.如图,AC⊥CB,DB⊥CB,垂足分别为C、B,AB=DC,求证:∠A=∠D.
20.已知如图,AB⊥BC,点B、C、D在同一水平线上.测得CD的长度为15m,在C,D处测得顶部A的仰角分别为37.5°、45°,求AB的高度.(结果精确到1m.参考数据:sin37.5°≈0.609,cos37.5°≈0.793,tan37.5°≈0.767)
解答题(共3小题,每小题8分,共24分)
21.已知关于x的一元二次方程x2+2x﹣k=0有两个不相等的实数根.
(1)求k的取值范围;
(2)若方程的两个不相等的实数根是a,b,求﹣的值.
22.如图,双曲线y=与直线y=kx+b交于点A(﹣8,1)、B(2,﹣4),与两坐标轴分别交于点C、D,已知点E(1,0),连接AE、BE.
(1)求m,k,b的值;
(2)求△ABE的面积;
(3)作直线ED,将直线ED向上平移n(n>0)个单位后,与双曲线y=有唯一交点,求n的值.
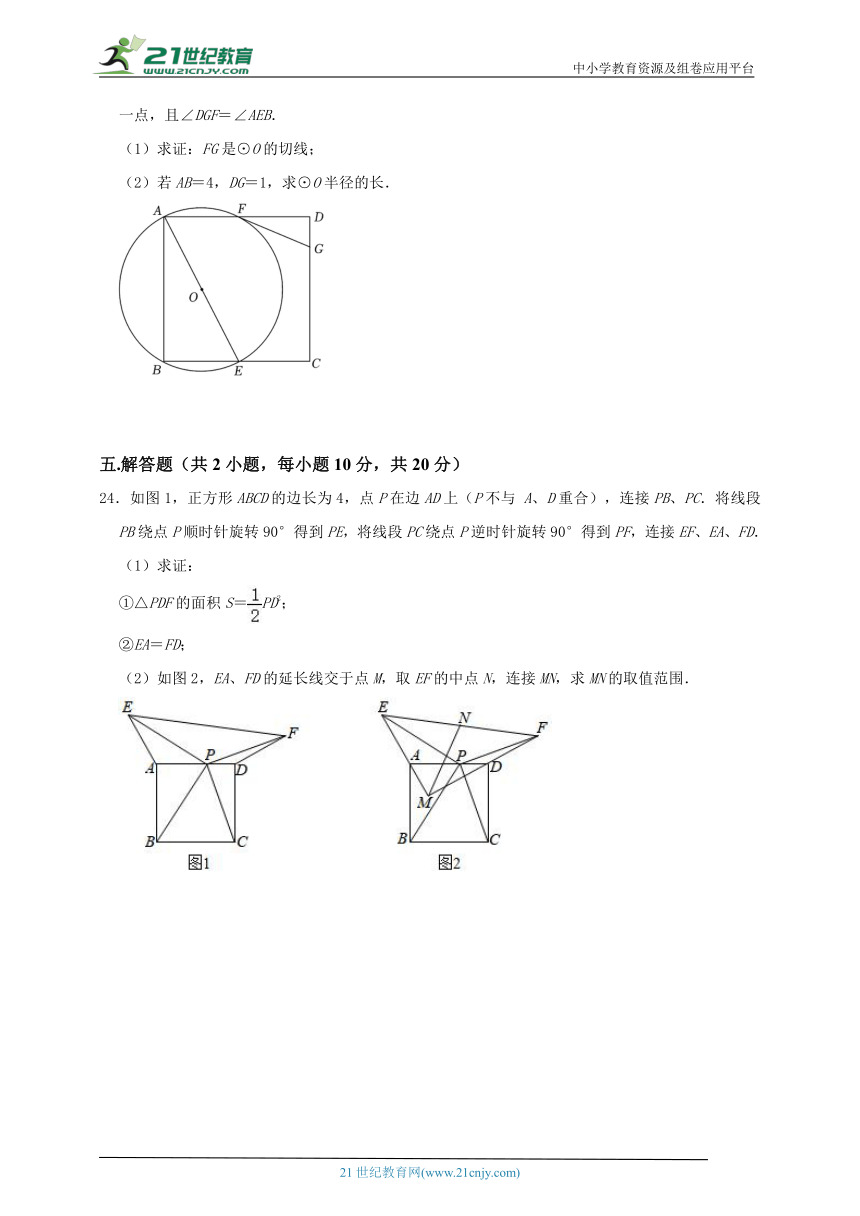
23.如图,点E为正方形ABCD的边BC上的一点,⊙O是△ABE的外接圆,与AD交于点F.G是CD上一点,且∠DGF=∠AEB.
(1)求证:FG是⊙O的切线;
(2)若AB=4,DG=1,求⊙O半径的长.
五.解答题(共2小题,每小题10分,共20分)
24.如图1,正方形ABCD的边长为4,点P在边AD上(P不与 A、D重合),连接PB、PC.将线段PB绕点P顺时针旋转90°得到PE,将线段PC绕点P逆时针旋转90°得到PF,连接EF、EA、FD.
(1)求证:
①△PDF的面积S=PD2;
②EA=FD;
(2)如图2,EA、FD的延长线交于点M,取EF的中点N,连接MN,求MN的取值范围.
25.如图,抛物线y=x2+bx+c与x轴交于A,B两点,点A,B分别位于原点的左、右两侧,BO=3AO=3,过点B的直线与y轴正半轴和抛物线的交点分别为C,D,BC=CD.
(1)求b,c的值;
(2)求直线BD的函数解析式;
(3)点P在抛物线的对称轴上且在x轴下方,点Q在射线BA上.当△ABD与△BPQ相似时,请直接写出所有满足条件的点Q的坐标.
2024年一模参考答案
选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D B C C A A A D
二、填空题
题号 11 12 13 14 15 16 17
答案 x≤2 3(x﹣2y)(x+2y) 1 (5,1)或(﹣1,5) 3. ①③. ①②④
三.解答题
18.解:,
①×2得:4x+2y=16③,
②+③得:
7x=21,
解得:x=3,
把x=3代入①得:
6+y=8,
解得:y=2,
∴原方程组的解为.
19.证明:∵AC⊥CB,DB⊥CB,
∴△ACB与△DBC均为直角三角形,
在Rt△ACB与Rt△DBC中,
,
∴Rt△ACB≌Rt△DBC(HL),
∴∠A=∠D,
20.解:由图可得:∠ABC=90°,∠ADB=45°,∠ACB=37.5°,
∴△ABD为等腰直角三角形,
∴AB=BD,
设AB=BD=xm,则BC=(x+15)m,
在Rt△ABC中,tan37.5°=,即0.767≈,
∴x≈49,
答:跳台AB的高度约为49m.
解答题(共3小题,每小题8分,共24分)
21.解:(1)∵方程有两个不相等的实数根,
∴Δ=b2﹣4ac=4+4k>0,
解得k>﹣1.
∴k的取值范围为k>﹣1;
(2)由根与系数关系得a+b=﹣2,a b=﹣k,
﹣===1.
22.解:(1)∵双曲线y=过点A(﹣8,1),
∴m=﹣8×1=﹣8,
又∵直线y=kx+b经过点A(﹣8,1)、B(2,﹣4),
∴,
解得k=﹣,b=﹣3,
答:m=﹣8,k=﹣,b=﹣3;
(2)由(1)可得反比例函数的关系式为y=,
直线AB的关系式为y=﹣x﹣3,
当y=0时,﹣x﹣3=0,解得x=﹣6,即C(﹣6,0),
∴OC=6,
由点E(1,0)可得OE=1,
∴EC=OE+OC=1+6=7,
∴S△ABE=S△ACE+S△BCE
=×7×1+×7×4
=;
(3)设直线DE的关系式为y=kx+b,D(0,﹣3),E(1,0)代入得,
b=﹣3,k+b=0,
∴k=3,b=﹣3,
∴直线DE的关系式为y=3x﹣3,
设DE平移后的关系式为y=3x﹣3+n,由于平移后与y=有唯一公共点,
即方程3x﹣3+n=有唯一解,
也就是关于x的方程3x2+(n﹣3)x+8=0有两个相等的实数根,
∴(n﹣3)2﹣4×3×8=0,
解得n=3+4,n=3﹣4(舍去),
∴n=3+4,
答:n的值为3+4.
23.证明:(1)连接OF,
∵AO=OF,
∴∠OAF=∠OFA,
∵四边形ABCD是正方形,
∴AF∥BE,
∴∠AEB=∠OAF,
∵∠DGF=∠AEB,
∴∠AFO=∠DGF,
∵四边形ABCD是正方形,
∴∠D=90°,
∴∠FGD+∠DFG=90°,
∴∠AFO+∠DFG=90°,
∴∠OFG=90°,
∴OF⊥FG,
∵点F是⊙O上的一点,
∴FG是⊙O的切线;
(2)解:连接EF,
∵⊙O是△ABE的外接圆,∠B=90°,
∴AE是⊙O的直径,
∴∠AFE=90°,
∵四边形ABCD是正方形,
∴∠BAF=∠ABE=90°,
∵四边形ABEF是矩形,
∴BE=AF,
∵∠DGF=∠AEB,∠D=∠B=90°,
∴△FDG∽△ABE,
∴,
∵四边形ABCD是正方形,
∴AB=BC=AD=4,
∴,
∴BE=2,
∴AE=,
∴OA=.
即⊙O半径的长为.
24.(1)证明:如图1,作FG⊥AD,交AD的延长线于点G,作EH⊥AD,交DA的延长线于点H.
①由旋转得,PF=CP,∠CPF=90°,
∵四边形ABCD是正方形,
∴∠PDC=90°,
∵∠FPG+∠DPC=90°,∠PCD+∠DPC=90°,
∴∠FPG=∠PCD,
∵∠G=∠PDC=90°,
∴△FPG≌△PCD(AAS),
∴FG=PD,
∴△PDF的面积S=PD FG=PD2.
②由①得,△FPG≌△PCD,
∴PD=FG,PG=CD=4,
同理,△EPH≌△PBA,
∴EH=AP,PH=BA=4,
∵AH=4﹣AP=PD,
∴AH=FG;
∵AP=4﹣PD=DG,
∴EH=DG;
∵∠H=∠G=90°,
∴△EAH≌△DFG(SAS),
∴EA=FD.
(2)如图2,在图1的基础上,作FL⊥EH于点L,则∠FLE=∠FLH=90°,
∴四边形HLFG是矩形,
∴LH=FG=AH,FL=GH=4+4=8;
∵EH=PA,AH=PD,
∴EH+AH=PA+PD=AD=4;
设PD=m,EL=n,(m>0,n≥0),则LH=AH=m,
∴n=4﹣2m;
∵EF2=EL2+FL2=n2+82=n2+64,
∴EF=,
∴EF随n的增大而增大;
由n=4﹣2m可知,n随m的增大而减小,
当m=2时,n最小=0,此时,EF最小==8;
若m=0,则n最大=4,此时,EF最大==4,
∵点P不与点A、D重合,
∴m>0,
∴n<4,EF<4,
∴EF的取值范围是8≤EF<,
∴4≤EF<;
∵∠ADM=∠GDF=∠HEA,∠DAM=∠HAE,
∴∠ADM+∠DAM=∠HEA+∠HAE=90°,
∴∠EMF=90°;
∵N是EF的中点,
∴MN=EF,
∴MN的取值范围是4≤MN<.
25.解:(1)∵BO=3AO=3,
∴点B(3,0),点A(﹣1,0),
∴抛物线解析式为:y=(x+1)(x﹣3)=x2﹣x﹣,
∴b=﹣,c=﹣;
(2)如图1,过点D作DE⊥AB于E,
∴CO∥DE,
∴,
∵BC=CD,BO=3,
∴=,
∴OE=,
∴点D横坐标为﹣,
∴点D坐标为(﹣,+1),
设直线BD的函数解析式为:y=kx+m,
由题意可得:,
解得:,
∴直线BD的函数解析式为y=﹣x+;
(3)∵点B(3,0),点A(﹣1,0),点D(﹣,+1),
∴AB=4,AD=2,BD=2+2,对称轴为直线x=1,
∵直线BD:y=﹣x+与y轴交于点C,
∴点C(0,),
∴OC=,
∵tan∠CBO==,
∴∠CBO=30°,
如图2,过点A作AK⊥BD于K,
∴AK=AB=2,
∴DK===2,
∴DK=AK,
∴∠ADB=45°,
如图,设对称轴与x轴的交点为N,即点N(1,0),
若∠CBO=∠PBO=30°,
∴BN=PN=2,BP=2PN,
∴PN=,BP=,
当△BAD∽△BPQ,
∴,
∴BQ==2+,
∴点Q(1﹣,0);
当△BAD∽△BQP,
∴,
∴BQ==4﹣,
∴点Q(﹣1+,0);
若∠PBO=∠ADB=45°,
∴BN=PN=2,BP=BN=2,
当△DAB∽△BPQ,
∴,
∴,
∴BQ=2+2
∴点Q(1﹣2,0);
当△BAD∽△PQB,
∴,
∴BQ==2﹣2,
∴点Q(5﹣2,0);
综上所述:满足条件的点Q的坐标为(1﹣,0)或(﹣1+,0)或(1﹣2,0)或(5﹣2,0).
1;邮箱:13794018491;学号:32253081
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
九年级数学总复习摸底测试卷(含参考答案)
满分:120分 考试时间:90分钟
一、选择题(本大题共10个小题,每题3分,满分30分)
1.在1,﹣2,0,这四个数中,最大的数是( )
A.1 B.﹣2 C.0 D.
2.如图,是由棱长都相等的四个小正方体组成的几何体.该几何体的左视图是( )
A. B. C. D.
3.下列运算正确的是( )
A.x2+2x2=3x4 B.(x3)4=x7
C.(2x+y)(2x﹣y)=2x2﹣y2 D.x÷x3=x﹣2
4.如图,AB为⊙O的切线,切点为B,连接OB、OA,交⊙O于点C,点D为优弧BC上一点,连接DC、DB,若∠A=20°,则∠D的大小为( )
A.20° B.35° C.25° D.15°
第4题图 第5题图
5.如图,边长为5的菱形ABCD对角线AC,BD交于点O,E是AB的中点,则EO的长为( )
A.10 B.5 C. D.
6.下面a,b的取值,能够说明命题“若a>b,则|a|>|b|”是假命题的是( )
A.a=3,b=2 B.a=3,b=﹣2 C.a=﹣3,b=﹣5 D.a=﹣3,b=5
7.若关于x的一元二次方程x2﹣2mx+m2﹣4m﹣1=0有两个实数根x1,x2,且(x1+2)(x2+2)﹣2x1x2=17,则m=( )
A.2或6 B.2或8 C.2 D.6
8.我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为6210文.如果每株椽的运费是3文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6210文能买多少株椽?设这批椽的数量为x株,则符合题意的方程是( )
A.3(x﹣1)= B.=3 C.3x﹣1= D.=3
9.如图,四边形ABCD内接于⊙O,AB=CD,A为中点,∠BDC=60°,则∠ADB等于( )
A.40° B.50° C.60° D.70°
第9题图 第10题图
10.(3分)如图,菱形ABCD的顶点分别在反比例函数y=和y=的图象上,若∠BCD=60°,则的值为( )
A. B. C. D.
二、填空题(本大题共7小题,每小题4分,共28分.)
11.如果式子在实数范围内有意义,则x的取值范围是 .
12.因式分解:3x2﹣12y2= .
13.已知a+2b=,3a+4b=,则a+b的值为 .
14.将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点F的坐标为 .
15.如图,正方形ABCD的边长为2,E,F分别是BC,CD的中点,连接AE,G为AE上的一点,且∠FGE=45°,则GF的长为 .
16.如图,CD为⊙O的直径,AB为⊙O中长度为定值的弦,AB<CD.作AE⊥CD于E,连接AC,BC,BE.下列四个结论中:①O到AB的距离为定值;②BE=BC;③当OE=AE时,∠ABC=67.5°或22.5°;④∠BAE+2∠ACD为定值.正确的是 .(填所有正确的序号)
第15题图 第16题图 第17题图
17.两个反比例函数和在第一象限内的图象如图所示,点P在的图象上,PC⊥x轴于点C,交的图象于点A,PD⊥y轴于点D,交的图象于点B,当点P在的图象上运动时,以下结论:
①△ODB与△OCA的面积相等;
②四边形PAOB的面积不会发生变化;
③PA与PB始终相等;
④2<k<4.
其中一定正确的是 .
三.解答题(共3小题,每小题6分,共18分)
18.解方程组:.
19.如图,AC⊥CB,DB⊥CB,垂足分别为C、B,AB=DC,求证:∠A=∠D.
20.已知如图,AB⊥BC,点B、C、D在同一水平线上.测得CD的长度为15m,在C,D处测得顶部A的仰角分别为37.5°、45°,求AB的高度.(结果精确到1m.参考数据:sin37.5°≈0.609,cos37.5°≈0.793,tan37.5°≈0.767)
解答题(共3小题,每小题8分,共24分)
21.已知关于x的一元二次方程x2+2x﹣k=0有两个不相等的实数根.
(1)求k的取值范围;
(2)若方程的两个不相等的实数根是a,b,求﹣的值.
22.如图,双曲线y=与直线y=kx+b交于点A(﹣8,1)、B(2,﹣4),与两坐标轴分别交于点C、D,已知点E(1,0),连接AE、BE.
(1)求m,k,b的值;
(2)求△ABE的面积;
(3)作直线ED,将直线ED向上平移n(n>0)个单位后,与双曲线y=有唯一交点,求n的值.
23.如图,点E为正方形ABCD的边BC上的一点,⊙O是△ABE的外接圆,与AD交于点F.G是CD上一点,且∠DGF=∠AEB.
(1)求证:FG是⊙O的切线;
(2)若AB=4,DG=1,求⊙O半径的长.
五.解答题(共2小题,每小题10分,共20分)
24.如图1,正方形ABCD的边长为4,点P在边AD上(P不与 A、D重合),连接PB、PC.将线段PB绕点P顺时针旋转90°得到PE,将线段PC绕点P逆时针旋转90°得到PF,连接EF、EA、FD.
(1)求证:
①△PDF的面积S=PD2;
②EA=FD;
(2)如图2,EA、FD的延长线交于点M,取EF的中点N,连接MN,求MN的取值范围.
25.如图,抛物线y=x2+bx+c与x轴交于A,B两点,点A,B分别位于原点的左、右两侧,BO=3AO=3,过点B的直线与y轴正半轴和抛物线的交点分别为C,D,BC=CD.
(1)求b,c的值;
(2)求直线BD的函数解析式;
(3)点P在抛物线的对称轴上且在x轴下方,点Q在射线BA上.当△ABD与△BPQ相似时,请直接写出所有满足条件的点Q的坐标.
2024年一模参考答案
选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D B C C A A A D
二、填空题
题号 11 12 13 14 15 16 17
答案 x≤2 3(x﹣2y)(x+2y) 1 (5,1)或(﹣1,5) 3. ①③. ①②④
三.解答题
18.解:,
①×2得:4x+2y=16③,
②+③得:
7x=21,
解得:x=3,
把x=3代入①得:
6+y=8,
解得:y=2,
∴原方程组的解为.
19.证明:∵AC⊥CB,DB⊥CB,
∴△ACB与△DBC均为直角三角形,
在Rt△ACB与Rt△DBC中,
,
∴Rt△ACB≌Rt△DBC(HL),
∴∠A=∠D,
20.解:由图可得:∠ABC=90°,∠ADB=45°,∠ACB=37.5°,
∴△ABD为等腰直角三角形,
∴AB=BD,
设AB=BD=xm,则BC=(x+15)m,
在Rt△ABC中,tan37.5°=,即0.767≈,
∴x≈49,
答:跳台AB的高度约为49m.
解答题(共3小题,每小题8分,共24分)
21.解:(1)∵方程有两个不相等的实数根,
∴Δ=b2﹣4ac=4+4k>0,
解得k>﹣1.
∴k的取值范围为k>﹣1;
(2)由根与系数关系得a+b=﹣2,a b=﹣k,
﹣===1.
22.解:(1)∵双曲线y=过点A(﹣8,1),
∴m=﹣8×1=﹣8,
又∵直线y=kx+b经过点A(﹣8,1)、B(2,﹣4),
∴,
解得k=﹣,b=﹣3,
答:m=﹣8,k=﹣,b=﹣3;
(2)由(1)可得反比例函数的关系式为y=,
直线AB的关系式为y=﹣x﹣3,
当y=0时,﹣x﹣3=0,解得x=﹣6,即C(﹣6,0),
∴OC=6,
由点E(1,0)可得OE=1,
∴EC=OE+OC=1+6=7,
∴S△ABE=S△ACE+S△BCE
=×7×1+×7×4
=;
(3)设直线DE的关系式为y=kx+b,D(0,﹣3),E(1,0)代入得,
b=﹣3,k+b=0,
∴k=3,b=﹣3,
∴直线DE的关系式为y=3x﹣3,
设DE平移后的关系式为y=3x﹣3+n,由于平移后与y=有唯一公共点,
即方程3x﹣3+n=有唯一解,
也就是关于x的方程3x2+(n﹣3)x+8=0有两个相等的实数根,
∴(n﹣3)2﹣4×3×8=0,
解得n=3+4,n=3﹣4(舍去),
∴n=3+4,
答:n的值为3+4.
23.证明:(1)连接OF,
∵AO=OF,
∴∠OAF=∠OFA,
∵四边形ABCD是正方形,
∴AF∥BE,
∴∠AEB=∠OAF,
∵∠DGF=∠AEB,
∴∠AFO=∠DGF,
∵四边形ABCD是正方形,
∴∠D=90°,
∴∠FGD+∠DFG=90°,
∴∠AFO+∠DFG=90°,
∴∠OFG=90°,
∴OF⊥FG,
∵点F是⊙O上的一点,
∴FG是⊙O的切线;
(2)解:连接EF,
∵⊙O是△ABE的外接圆,∠B=90°,
∴AE是⊙O的直径,
∴∠AFE=90°,
∵四边形ABCD是正方形,
∴∠BAF=∠ABE=90°,
∵四边形ABEF是矩形,
∴BE=AF,
∵∠DGF=∠AEB,∠D=∠B=90°,
∴△FDG∽△ABE,
∴,
∵四边形ABCD是正方形,
∴AB=BC=AD=4,
∴,
∴BE=2,
∴AE=,
∴OA=.
即⊙O半径的长为.
24.(1)证明:如图1,作FG⊥AD,交AD的延长线于点G,作EH⊥AD,交DA的延长线于点H.
①由旋转得,PF=CP,∠CPF=90°,
∵四边形ABCD是正方形,
∴∠PDC=90°,
∵∠FPG+∠DPC=90°,∠PCD+∠DPC=90°,
∴∠FPG=∠PCD,
∵∠G=∠PDC=90°,
∴△FPG≌△PCD(AAS),
∴FG=PD,
∴△PDF的面积S=PD FG=PD2.
②由①得,△FPG≌△PCD,
∴PD=FG,PG=CD=4,
同理,△EPH≌△PBA,
∴EH=AP,PH=BA=4,
∵AH=4﹣AP=PD,
∴AH=FG;
∵AP=4﹣PD=DG,
∴EH=DG;
∵∠H=∠G=90°,
∴△EAH≌△DFG(SAS),
∴EA=FD.
(2)如图2,在图1的基础上,作FL⊥EH于点L,则∠FLE=∠FLH=90°,
∴四边形HLFG是矩形,
∴LH=FG=AH,FL=GH=4+4=8;
∵EH=PA,AH=PD,
∴EH+AH=PA+PD=AD=4;
设PD=m,EL=n,(m>0,n≥0),则LH=AH=m,
∴n=4﹣2m;
∵EF2=EL2+FL2=n2+82=n2+64,
∴EF=,
∴EF随n的增大而增大;
由n=4﹣2m可知,n随m的增大而减小,
当m=2时,n最小=0,此时,EF最小==8;
若m=0,则n最大=4,此时,EF最大==4,
∵点P不与点A、D重合,
∴m>0,
∴n<4,EF<4,
∴EF的取值范围是8≤EF<,
∴4≤EF<;
∵∠ADM=∠GDF=∠HEA,∠DAM=∠HAE,
∴∠ADM+∠DAM=∠HEA+∠HAE=90°,
∴∠EMF=90°;
∵N是EF的中点,
∴MN=EF,
∴MN的取值范围是4≤MN<.
25.解:(1)∵BO=3AO=3,
∴点B(3,0),点A(﹣1,0),
∴抛物线解析式为:y=(x+1)(x﹣3)=x2﹣x﹣,
∴b=﹣,c=﹣;
(2)如图1,过点D作DE⊥AB于E,
∴CO∥DE,
∴,
∵BC=CD,BO=3,
∴=,
∴OE=,
∴点D横坐标为﹣,
∴点D坐标为(﹣,+1),
设直线BD的函数解析式为:y=kx+m,
由题意可得:,
解得:,
∴直线BD的函数解析式为y=﹣x+;
(3)∵点B(3,0),点A(﹣1,0),点D(﹣,+1),
∴AB=4,AD=2,BD=2+2,对称轴为直线x=1,
∵直线BD:y=﹣x+与y轴交于点C,
∴点C(0,),
∴OC=,
∵tan∠CBO==,
∴∠CBO=30°,
如图2,过点A作AK⊥BD于K,
∴AK=AB=2,
∴DK===2,
∴DK=AK,
∴∠ADB=45°,
如图,设对称轴与x轴的交点为N,即点N(1,0),
若∠CBO=∠PBO=30°,
∴BN=PN=2,BP=2PN,
∴PN=,BP=,
当△BAD∽△BPQ,
∴,
∴BQ==2+,
∴点Q(1﹣,0);
当△BAD∽△BQP,
∴,
∴BQ==4﹣,
∴点Q(﹣1+,0);
若∠PBO=∠ADB=45°,
∴BN=PN=2,BP=BN=2,
当△DAB∽△BPQ,
∴,
∴,
∴BQ=2+2
∴点Q(1﹣2,0);
当△BAD∽△PQB,
∴,
∴BQ==2﹣2,
∴点Q(5﹣2,0);
综上所述:满足条件的点Q的坐标为(1﹣,0)或(﹣1+,0)或(1﹣2,0)或(5﹣2,0).
1;邮箱:13794018491;学号:32253081
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
