广东省深圳市2023 — 2024学年深圳第二学期33校联考九年级数学4月质量检测(含答案)
文档属性
| 名称 | 广东省深圳市2023 — 2024学年深圳第二学期33校联考九年级数学4月质量检测(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 594.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-06 10:22:42 | ||
图片预览



文档简介
2024年初三年级质量检测
数学(4月)
本试卷分为第 I 卷(选择题)和第Ⅱ卷(非选择题)两部分,第I 卷为1-10题,共30
分,第Ⅱ卷为11-22题,共70分。全卷共计100分,考试时间为90分钟。
注意事项:
1、答题前,请将学校、姓名、班级、考场和座位号写在答题卡指定位置,将条形码贴在答
题卡指定位置。
2、选择题答案,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动请用2B橡皮擦 干净后,再涂其它答案,不能答在试题卷上。非选择题,答题不能超出题目指定区域。
3、考试结束,监考人员将答题卡收回。
第 I 卷 (本卷共计30分)
一 . 选择题:(每小题只有一个选项符合题意,每小题3分,共计30分)
1.下列四个数中,属于无理数的是(***)
A.0 B.1.33 D.√3
C.
2.下列运算正确的是(***)
A.3x-x=3 B.2a+4a=6a
C.4xy-3xy=xy D.2a+3b=5ab
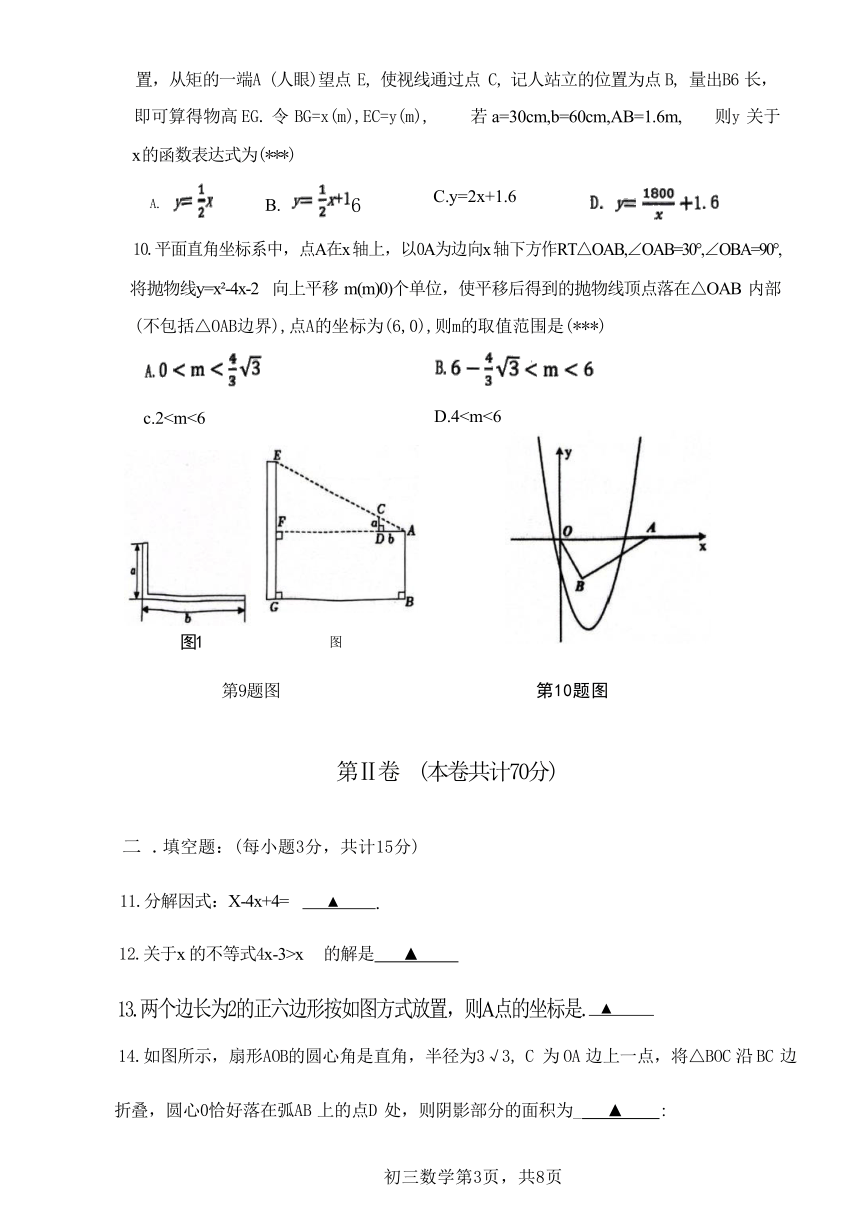
3.如图所示,已知直线 a/l b,∠1=110°,∠2=62°, 则∠3的度数为(***)
A.48° B.49° C.50° D.52°
(
第8题图
) (
第6题图
)第3题图
初三数学第1页,共8页
4.下列变形,正确的是(***)
A. 由 3x+6=23-2x, 移项,得3x-2x=23+6
B. 由 2x-(x+10)=5x, 去括号,得2x-x+10=5x
C. 由4 x-7x+2x =3, 合并同类项,得- x=3
去分母,得9x=3-(2x-1)
5.春节期间电影《热辣滚烫》上映的第一天票房约为3亿元,第二、三天单日票房持续增长, 三天累计票房9.63亿元,若第二、三天单日票房增长率相同,设平均每天票房的增长率为x,
则根据题意,下列方程正确的是(***)
A.3(1+x)=9.63 B.3(1+x) =9.63
C.3(1+x)+3(1+x) =9.63 D.3+3(1+x)+3(1+x) =9.63
6.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A) 与电阻R (单位:Ω)是反
比例函数关系,它的图象如图所示.下列说法正确的是(***)
A. 函数解析式为 B. 蓄电池的电压是18V
C. 当 R=6Ω 时 ,I=4A D. 当 I≤10A 时, R≥3.6Ω
7.某校八年级学生参加体质健康测试,有一组9个女生做一分钟的仰卧起坐个数如表中数据
所示,则这组仰卧起坐个数的众数和中位数分别是(***)
学生(序号) 1号 2号 3号 4号 5号 6号 7号 8号 9号
仰卧起坐个数 52 56 50 50 48 58 52 50 54
A. 众数是58,中位数是48 B. 众数是58,中位数是52
C. 众数是50,中位数是48 D. 众数是50,中位数是52
8.如图,在△ABC中,AB=AC,∠BAC=36°,以点B 为圆心,以BC为半径作弧交 AB于点D,
再分别以 C,D 为圆心,以大长为半径件现,两双相交于点B作射线8交AC于点R
连接DF. 以下结论不正确的是(***)
A.AD=CF B.BC=AF C. ∠ABE=36 D. ∠CFD=108°
9.西周数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边放置成如图2的位
初三数学第2页,共8页
置,从矩的一端A (人眼)望点 E, 使视线通过点 C, 记人站立的位置为点 B, 量出B6 长,
即可算得物高 EG. 令 BG=x(m),EC=y(m), 若 a=30cm,b=60cm,AB=1.6m, 则y 关于
x 的函数表达式为(***)
A. B. 6 C.y=2x+1.6
10.平面直角坐标系中,点A在x 轴上,以0A为边向x 轴下方作RT△OAB,∠OAB=30°,∠OBA=90°, 将抛物线y=x -4x-2 向上平移 m(m)0)个单位,使平移后得到的抛物线顶点落在△OAB 内部
(不包括△OAB边界),点A的坐标为(6,0),则m的取值范围是(***)
c.2(
图2
)图1
第9题图
D.4第10题图
第Ⅱ卷 (本卷共计70分)
二 .填空题:(每小题3分,共计15分)
11.分解因式:X-4x+4= ▲ .
12.关于x 的不等式4x-3>x 的解是 ▲
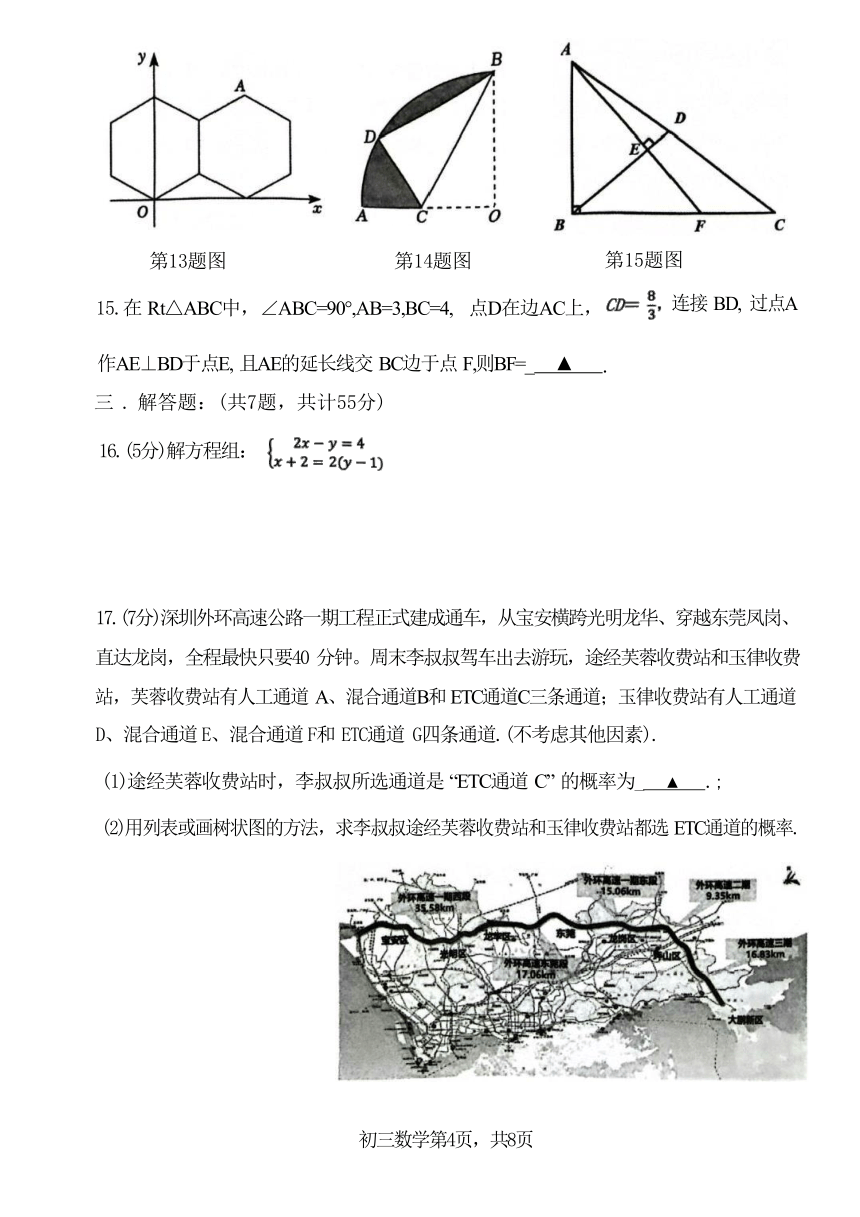
13.两个边长为2的正六边形按如图方式放置,则A点的坐标是. ▲
14.如图所示,扇形AOB的圆心角是直角,半径为3√3, C 为 OA 边上一点,将△BOC 沿 BC 边
折叠,圆心0恰好落在弧AB 上的点D 处,则阴影部分的面积为_ ▲ :
初三数学第3页,共8页
第13题图
第14题图
第15题图
15.在 Rt△ABC中,∠ABC=90°,AB=3,BC=4, 点D在边AC上,
连接 BD, 过点A
作AE⊥BD于点E, 且AE的延长线交 BC边于点 F,则BF=_ ▲ .
三 . 解答题:(共7题,共计55分)
16.(5分)解方程组:
17.(7分)深圳外环高速公路一期工程正式建成通车,从宝安横跨光明龙华、穿越东莞凤岗、 直达龙岗,全程最快只要40 分钟。周末李叔叔驾车出去游玩,途经芙蓉收费站和玉律收费 站,芙蓉收费站有人工通道 A、混合通道B和 ETC通道C三条通道;玉律收费站有人工通道
D、混合通道 E、混合通道 F和 ETC通道 G四条通道.(不考虑其他因素).
(1)途经芙蓉收费站时,李叔叔所选通道是 “ETC通道 C” 的概率为_ ▲ .;
(2)用列表或画树状图的方法,求李叔叔途经芙蓉收费站和玉律收费站都选 ETC通道的概率.
初三数学第4页,共8页
18.(8分)电动汽车的续航里程也可以称作续航能力,是指电动汽车的动力蓄电池在充满电 的状态下可连续行驶的总里程,它是电动汽车重要的经济性指标。高速路况状态下,电动车 的续航里程除了会受到环境温度的影响,还和汽车的行驶速度有关.某科研团队为了分析续
航里程与速度的关系,进行了如下的探究:
下面是他们的探究过程,请补充完整:
(1)他们调取了某款电动汽车在某个特定温度下的续航里程与速度的有关数据:
速度 (千米/小时) 10 20 30 40 60 80 100 120 140 160
续航里程 (千米) 100 340 460 530 580 560 500 430 380 310
则设_ ▲ 为 y, ▲ 为x,y 是x 的函数;
(2)建立平面直角坐标系,在给出的格点图中描出表中各对对应值为坐标的点,画出该函
数的图象;
(3)结合画出的函数图象,下列说法正确的有_ ▲
①y 随 x 的增大而减小;
②当汽车的速度在60千米/小时左右时,汽车的续航里程最大;
③实验表明,汽车的速度过快或过慢时,汽车的续航里程都会变小.
(4)若想要该车辆的续航里程保持在460千米以上,该车的车速大约控制在 ▲ 至
千米/小时范围内
初三数学第5页,共8页
19 . (8分)某店有A、B两种熊猫玩偶,已知每个A款熊猫玩偶的售价是每个B款熊猫玩偶售
价的学倍,顾客用150元购买A 款熊猫玩偶的数量比用150元购买B 款熊猫玩偶的数量少1个.
(1)求每个B 款熊猫玩偶的售价为多少元
(2)经统计,该店每月卖出A款熊猫玩偶100个,每个A 款熊猫玩偶的利润为16元.为了 尽快减少库存,该店决定采取适当的降价措施。调查发现,每个A 款熊猫玩偶的售价每降低 2元,那么平均每月可多售出20个.该店想每月销售A 款熊猫玩偶的利润达到1200元,每
个A 款熊猫玩偶应降价多少元
20.(8分)如图,在等腰△ABC中,AB=BC,BO 平分∠ABC, 过点A作 AD/IBC交 BO的延长
线于 D, 连接 CD, 过点 D作DE⊥BD交 BC的延长线于 E。
(1)判断四边形 ABCD的形状,并说明理由;
(2)若DE=10,sin 求四边形
ABCD的面积。
21.(9分)【项目式学习】
项目主题:设计落地窗的遮阳篷.
项目背景:小明家的窗户朝南,窗户的高度AB=2m, 为了遮挡太阳光,小明做了以下遮阳蓬
的设计方案,请根据不同设计方案完成以下任务。
方案1:直角形遮阳篷
如图1,小明设计的第一个方案为直角形遮阳篷 BCD, 点C在AB的延长线上CD⊥AC.
( 1 ) 若 BC=0.5m,CD=1m, 则支撑杆BD= A m.
初三数学第6页,共8页
(2)小明发现上述方案不能很好发挥遮阳作用,如图2,他观察到此地一年中的正午时刻, 太阳光与地平面的最小夹角为a, 最大夹角为β。小明查阅资料,计算出1 , ’ 为了让遮阳篷既能最大限度地使冬天温暖的阳光射入室内(太阳光与BD平行),又能最大限
度地遮挡夏天炎热的阳光(太阳光与AD平行)。请求出图2中BC,CD 的长度.
图 2
方案2:抛物线形遮阳篷
(3)如图3,为了美观及实用性,小明在(2)的基础上将CD 边改为抛物线形可伸缩的遮阳
篷(F 为抛物线的顶点,DF段可伸缩),且∠CFD=90°,BC,CD的长保持不变.若以C为原点,
CD 方向为x 轴,BC 方向为y 轴。①求该二次函数的表达式.②若某时刻太阳光与水平地面夹 角θ的正切值 使阳光最大限度地摄入室内,求遮阳蓬点D 上升的高度最小值(即点
D’到 CD 的距离)
图 3
22.(10分)在学习图形的旋转时,创新小组同学们借助三角形和菱形感受旋转带来图形变
化规律和性质
【操作探究】
(1)如图1,已知△ABC,∠C=90, 将△ABC绕着直角边AC中点G旋转,得到△DEF, 当△
DEF的顶点D恰好落在△ABC的斜边AB上时,斜边 DE与 AC交于点 H。
①猜想:∠ADC= A
②证明:△DGH∽△ADH.
【问题解决】
(2)在(1)的条件下,已知 AC=4,BC=3, 求CH 的长.
图 1
【拓展提升】
(3)如图2,在菱形ABCD 中 ,AC=8,BD=6,将菱形ABCD绕着 AB 中点M 顺时针旋转,得到菱 形 EFGH, 当菱形EFGH的顶点 E 分别恰好落在菱形ABCD的 AD 边和对角线BD上时,菱形 EFGH
的边与 BC 边相交于点N,请直接写出 BN的长.
图 2
备用图
(
……………………6分
)
2024年(4月)初三年级质量检测数学
参考答案及评分标准
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D C A C D D D D B B
二、填空题
题号 11 12 13 14 15
答案 (x-2) x>1 (2 ,4)
三 、解答题
16.解:
解:化简得, ……… … …………1分
将②×2,得2x-4y=-8,……………③
将③ - ①,得3y=-12,y=4. … … ……3分
原方程组 ………………5分
17.(1) ………………………………………………………………………3分
(
(2)解法
一:
A
B
c
D
E
F
G
D
E
F
G
D
E
F
G
开
始
)
共有12种可能的结果,其中都选 ETC 通道的有1种,
(
;……………………………8分
)途径芙蓉收费站和玉率收费站都选 ETC 通道的概率为.
解法二:
A B C
D (A,D) (B,D) (C,D)
E (A,E) (B,E) (C,E)
F (A,F) (B,F) (C,F)
G (A,G) (B,G) (C,G)
… ……6分
共有12种可能的结果,其中都选 ETC 通道的有1种,
途径芙蓉收费站和玉率收费站都选 ETC 通道的概率为 · ……………………………8分
(备注:①解法一中,12种等可能结果没有列举出来不扣分,即“树状图”正确3分,最
后结论2分;②解法二中,表格中没有结果表示,只作标记如只打 √,扣2分)
18(1)解:(1) ∵y 是 x 的函数,
∴速度为 x, 续航里程为 y………………………2分(每空1分)
(2)该函数的图象如图所示:
………………4分
(3)②③.………………………6分(答案不完整不给分)
(4)根据图象可知:30,110 .………………………8分(每空1分)
(备注:(2)问图像不平滑扣1分,(4)问第2空答案小于120,大于110均可给分)
19.(1)解:设每个B 款熊猫玩偶的售价x 元,则每个A 款熊猫玩偶的售价
由题意得 · ……… …………………2分
解得:x=25 … …… ………3分
经检验,x=25 是原方程的解,且符合题意, ……………………………4分
答:每台 B 款电器的售价为25元.
(2)每个A 款熊猫玩偶应降价m 元,
由题意得(16-m)( , …………………………5分
整理得:m -6m+40=0,
解得:m=10,mz=-4,……………………………7 分
∵为了尽快减少库存,
∴m=10.
答:每个A 款熊猫玩偶应降价10元.………………………………8分
(备注:第(2)中解正确但没有舍根的情况,只扣1分;设未知数的表述、未作答或答的
表述不规范的情况,扣1分)
20.证明:(1)四边形 ABCD是菱形
∵AB=BC,BO 平分∠ABC,
∴AC⊥BD,AO=CO.
∵AD//BE,
∴∠ADO=∠CBO
∴△ADO ≌ △CBO(AAS) ……………………………………………………2分
∴AD=BC
∴四边形 ABCD 是平行四边形.…………………………3分
∵AB=BC,
∴四边形 ABCD 是菱形.……………4 分
解:(2)∵OC//DE,O 是 BD的中点,
5.……………………………5分
∵AD//BE,
∴∠DAO=∠BCO
设 BO=X,则 BC=√5X.
……………………………6分
由RT△BOC得,X +5 =(√5x)
(
…………
……………………7
分
)·
:
即
(
是菱形
)∵四边形 ABCD
∴BD=2BO=5,AC=2CO=10
5… ……… ……………………8分
(备注:第(1)按步骤给分即可;第(2)问方法较多,按照步骤给分。)
21解:(1) m ………… ………2分
解:(2)由题意得: CDIAM,BDⅡAE,∠C=∠CAM=90°,
∵CDⅡAM,
∴∠CDA=∠DAM=β,
∵BDⅡAE,
∴∠BDA=∠EAD,
∴∠CDA-∠BDA=∠DAM-∠EAD,
∴∠CDB=∠EAM=a
在RT△CBD中,∠C=90°,
∴设 BC=x,CD=3x.
在RT△ACD 中,∠C=90°,
……… … … 3分
……4分
解得
. ………………5分
(备注:最后一步写错一个答案扣1分。)
解:(3)①由F 为抛物线顶点,可知FC=FD,
∵∠CFD=90°,
∴△FCD 为等腰直角三角形.
由二次函数对称性可知, F(1,1)
(
设二次函数为
y
=ax(x-2),
代入
F(1,1)
得
1=a(-1),
解得
a=-
1
∴y
关于
x
的关系式为:
y
=-x(x-2)=-x +2x
6
分
)
②BD '光线与水平方向的夹角为0,过 D'作x 轴的垂线交x 轴于点 E,
过日作y轴的重线,两条理线交于点H即
设 D'H=2m,BH=3m, 则点D(3m, ),……………………………7分
代入y=-x(x-2) 得 化简得27m -12m-2=0
解得, (答案不合理,舍去)……………………………8分
∴遮阳蓬点 D 上升的高度最小值为(… ……………………9分
22.(1) ① 90° ;……………………………1分
证明:②由旋转的性质可知,∠HDG=∠HAD
∵∠AHD=∠DHG,
∴△HDG~△HAD ………………………………3分
解:(2)∵AC=4,BC=3,
由勾股定理得,AC= √3 +4 =5,
∵△DEF的锐角顶点 D 恰好落在△ABC的斜边AB上,
∴AG=DG=GC,A、D、C 在以G 为圆心AG为半径的圆上.
∴∠ADC=90°
………
∵△HDG~△HAD
……………4分
设GH=5x, 则DH=8x,AH=5x+2
解得 经检验, 是方程的解……………………………5分
………
……6分
(3) 和 …… …10分(备注:对1个答案给2分。)
数学(4月)
本试卷分为第 I 卷(选择题)和第Ⅱ卷(非选择题)两部分,第I 卷为1-10题,共30
分,第Ⅱ卷为11-22题,共70分。全卷共计100分,考试时间为90分钟。
注意事项:
1、答题前,请将学校、姓名、班级、考场和座位号写在答题卡指定位置,将条形码贴在答
题卡指定位置。
2、选择题答案,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动请用2B橡皮擦 干净后,再涂其它答案,不能答在试题卷上。非选择题,答题不能超出题目指定区域。
3、考试结束,监考人员将答题卡收回。
第 I 卷 (本卷共计30分)
一 . 选择题:(每小题只有一个选项符合题意,每小题3分,共计30分)
1.下列四个数中,属于无理数的是(***)
A.0 B.1.33 D.√3
C.
2.下列运算正确的是(***)
A.3x-x=3 B.2a+4a=6a
C.4xy-3xy=xy D.2a+3b=5ab
3.如图所示,已知直线 a/l b,∠1=110°,∠2=62°, 则∠3的度数为(***)
A.48° B.49° C.50° D.52°
(
第8题图
) (
第6题图
)第3题图
初三数学第1页,共8页
4.下列变形,正确的是(***)
A. 由 3x+6=23-2x, 移项,得3x-2x=23+6
B. 由 2x-(x+10)=5x, 去括号,得2x-x+10=5x
C. 由4 x-7x+2x =3, 合并同类项,得- x=3
去分母,得9x=3-(2x-1)
5.春节期间电影《热辣滚烫》上映的第一天票房约为3亿元,第二、三天单日票房持续增长, 三天累计票房9.63亿元,若第二、三天单日票房增长率相同,设平均每天票房的增长率为x,
则根据题意,下列方程正确的是(***)
A.3(1+x)=9.63 B.3(1+x) =9.63
C.3(1+x)+3(1+x) =9.63 D.3+3(1+x)+3(1+x) =9.63
6.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A) 与电阻R (单位:Ω)是反
比例函数关系,它的图象如图所示.下列说法正确的是(***)
A. 函数解析式为 B. 蓄电池的电压是18V
C. 当 R=6Ω 时 ,I=4A D. 当 I≤10A 时, R≥3.6Ω
7.某校八年级学生参加体质健康测试,有一组9个女生做一分钟的仰卧起坐个数如表中数据
所示,则这组仰卧起坐个数的众数和中位数分别是(***)
学生(序号) 1号 2号 3号 4号 5号 6号 7号 8号 9号
仰卧起坐个数 52 56 50 50 48 58 52 50 54
A. 众数是58,中位数是48 B. 众数是58,中位数是52
C. 众数是50,中位数是48 D. 众数是50,中位数是52
8.如图,在△ABC中,AB=AC,∠BAC=36°,以点B 为圆心,以BC为半径作弧交 AB于点D,
再分别以 C,D 为圆心,以大长为半径件现,两双相交于点B作射线8交AC于点R
连接DF. 以下结论不正确的是(***)
A.AD=CF B.BC=AF C. ∠ABE=36 D. ∠CFD=108°
9.西周数学家商高总结了用“矩”(如图1)测量物高的方法:把矩的两边放置成如图2的位
初三数学第2页,共8页
置,从矩的一端A (人眼)望点 E, 使视线通过点 C, 记人站立的位置为点 B, 量出B6 长,
即可算得物高 EG. 令 BG=x(m),EC=y(m), 若 a=30cm,b=60cm,AB=1.6m, 则y 关于
x 的函数表达式为(***)
A. B. 6 C.y=2x+1.6
10.平面直角坐标系中,点A在x 轴上,以0A为边向x 轴下方作RT△OAB,∠OAB=30°,∠OBA=90°, 将抛物线y=x -4x-2 向上平移 m(m)0)个单位,使平移后得到的抛物线顶点落在△OAB 内部
(不包括△OAB边界),点A的坐标为(6,0),则m的取值范围是(***)
c.2
图2
)图1
第9题图
D.4
第Ⅱ卷 (本卷共计70分)
二 .填空题:(每小题3分,共计15分)
11.分解因式:X-4x+4= ▲ .
12.关于x 的不等式4x-3>x 的解是 ▲
13.两个边长为2的正六边形按如图方式放置,则A点的坐标是. ▲
14.如图所示,扇形AOB的圆心角是直角,半径为3√3, C 为 OA 边上一点,将△BOC 沿 BC 边
折叠,圆心0恰好落在弧AB 上的点D 处,则阴影部分的面积为_ ▲ :
初三数学第3页,共8页
第13题图
第14题图
第15题图
15.在 Rt△ABC中,∠ABC=90°,AB=3,BC=4, 点D在边AC上,
连接 BD, 过点A
作AE⊥BD于点E, 且AE的延长线交 BC边于点 F,则BF=_ ▲ .
三 . 解答题:(共7题,共计55分)
16.(5分)解方程组:
17.(7分)深圳外环高速公路一期工程正式建成通车,从宝安横跨光明龙华、穿越东莞凤岗、 直达龙岗,全程最快只要40 分钟。周末李叔叔驾车出去游玩,途经芙蓉收费站和玉律收费 站,芙蓉收费站有人工通道 A、混合通道B和 ETC通道C三条通道;玉律收费站有人工通道
D、混合通道 E、混合通道 F和 ETC通道 G四条通道.(不考虑其他因素).
(1)途经芙蓉收费站时,李叔叔所选通道是 “ETC通道 C” 的概率为_ ▲ .;
(2)用列表或画树状图的方法,求李叔叔途经芙蓉收费站和玉律收费站都选 ETC通道的概率.
初三数学第4页,共8页
18.(8分)电动汽车的续航里程也可以称作续航能力,是指电动汽车的动力蓄电池在充满电 的状态下可连续行驶的总里程,它是电动汽车重要的经济性指标。高速路况状态下,电动车 的续航里程除了会受到环境温度的影响,还和汽车的行驶速度有关.某科研团队为了分析续
航里程与速度的关系,进行了如下的探究:
下面是他们的探究过程,请补充完整:
(1)他们调取了某款电动汽车在某个特定温度下的续航里程与速度的有关数据:
速度 (千米/小时) 10 20 30 40 60 80 100 120 140 160
续航里程 (千米) 100 340 460 530 580 560 500 430 380 310
则设_ ▲ 为 y, ▲ 为x,y 是x 的函数;
(2)建立平面直角坐标系,在给出的格点图中描出表中各对对应值为坐标的点,画出该函
数的图象;
(3)结合画出的函数图象,下列说法正确的有_ ▲
①y 随 x 的增大而减小;
②当汽车的速度在60千米/小时左右时,汽车的续航里程最大;
③实验表明,汽车的速度过快或过慢时,汽车的续航里程都会变小.
(4)若想要该车辆的续航里程保持在460千米以上,该车的车速大约控制在 ▲ 至
千米/小时范围内
初三数学第5页,共8页
19 . (8分)某店有A、B两种熊猫玩偶,已知每个A款熊猫玩偶的售价是每个B款熊猫玩偶售
价的学倍,顾客用150元购买A 款熊猫玩偶的数量比用150元购买B 款熊猫玩偶的数量少1个.
(1)求每个B 款熊猫玩偶的售价为多少元
(2)经统计,该店每月卖出A款熊猫玩偶100个,每个A 款熊猫玩偶的利润为16元.为了 尽快减少库存,该店决定采取适当的降价措施。调查发现,每个A 款熊猫玩偶的售价每降低 2元,那么平均每月可多售出20个.该店想每月销售A 款熊猫玩偶的利润达到1200元,每
个A 款熊猫玩偶应降价多少元
20.(8分)如图,在等腰△ABC中,AB=BC,BO 平分∠ABC, 过点A作 AD/IBC交 BO的延长
线于 D, 连接 CD, 过点 D作DE⊥BD交 BC的延长线于 E。
(1)判断四边形 ABCD的形状,并说明理由;
(2)若DE=10,sin 求四边形
ABCD的面积。
21.(9分)【项目式学习】
项目主题:设计落地窗的遮阳篷.
项目背景:小明家的窗户朝南,窗户的高度AB=2m, 为了遮挡太阳光,小明做了以下遮阳蓬
的设计方案,请根据不同设计方案完成以下任务。
方案1:直角形遮阳篷
如图1,小明设计的第一个方案为直角形遮阳篷 BCD, 点C在AB的延长线上CD⊥AC.
( 1 ) 若 BC=0.5m,CD=1m, 则支撑杆BD= A m.
初三数学第6页,共8页
(2)小明发现上述方案不能很好发挥遮阳作用,如图2,他观察到此地一年中的正午时刻, 太阳光与地平面的最小夹角为a, 最大夹角为β。小明查阅资料,计算出1 , ’ 为了让遮阳篷既能最大限度地使冬天温暖的阳光射入室内(太阳光与BD平行),又能最大限
度地遮挡夏天炎热的阳光(太阳光与AD平行)。请求出图2中BC,CD 的长度.
图 2
方案2:抛物线形遮阳篷
(3)如图3,为了美观及实用性,小明在(2)的基础上将CD 边改为抛物线形可伸缩的遮阳
篷(F 为抛物线的顶点,DF段可伸缩),且∠CFD=90°,BC,CD的长保持不变.若以C为原点,
CD 方向为x 轴,BC 方向为y 轴。①求该二次函数的表达式.②若某时刻太阳光与水平地面夹 角θ的正切值 使阳光最大限度地摄入室内,求遮阳蓬点D 上升的高度最小值(即点
D’到 CD 的距离)
图 3
22.(10分)在学习图形的旋转时,创新小组同学们借助三角形和菱形感受旋转带来图形变
化规律和性质
【操作探究】
(1)如图1,已知△ABC,∠C=90, 将△ABC绕着直角边AC中点G旋转,得到△DEF, 当△
DEF的顶点D恰好落在△ABC的斜边AB上时,斜边 DE与 AC交于点 H。
①猜想:∠ADC= A
②证明:△DGH∽△ADH.
【问题解决】
(2)在(1)的条件下,已知 AC=4,BC=3, 求CH 的长.
图 1
【拓展提升】
(3)如图2,在菱形ABCD 中 ,AC=8,BD=6,将菱形ABCD绕着 AB 中点M 顺时针旋转,得到菱 形 EFGH, 当菱形EFGH的顶点 E 分别恰好落在菱形ABCD的 AD 边和对角线BD上时,菱形 EFGH
的边与 BC 边相交于点N,请直接写出 BN的长.
图 2
备用图
(
……………………6分
)
2024年(4月)初三年级质量检测数学
参考答案及评分标准
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D C A C D D D D B B
二、填空题
题号 11 12 13 14 15
答案 (x-2) x>1 (2 ,4)
三 、解答题
16.解:
解:化简得, ……… … …………1分
将②×2,得2x-4y=-8,……………③
将③ - ①,得3y=-12,y=4. … … ……3分
原方程组 ………………5分
17.(1) ………………………………………………………………………3分
(
(2)解法
一:
A
B
c
D
E
F
G
D
E
F
G
D
E
F
G
开
始
)
共有12种可能的结果,其中都选 ETC 通道的有1种,
(
;……………………………8分
)途径芙蓉收费站和玉率收费站都选 ETC 通道的概率为.
解法二:
A B C
D (A,D) (B,D) (C,D)
E (A,E) (B,E) (C,E)
F (A,F) (B,F) (C,F)
G (A,G) (B,G) (C,G)
… ……6分
共有12种可能的结果,其中都选 ETC 通道的有1种,
途径芙蓉收费站和玉率收费站都选 ETC 通道的概率为 · ……………………………8分
(备注:①解法一中,12种等可能结果没有列举出来不扣分,即“树状图”正确3分,最
后结论2分;②解法二中,表格中没有结果表示,只作标记如只打 √,扣2分)
18(1)解:(1) ∵y 是 x 的函数,
∴速度为 x, 续航里程为 y………………………2分(每空1分)
(2)该函数的图象如图所示:
………………4分
(3)②③.………………………6分(答案不完整不给分)
(4)根据图象可知:30,110 .………………………8分(每空1分)
(备注:(2)问图像不平滑扣1分,(4)问第2空答案小于120,大于110均可给分)
19.(1)解:设每个B 款熊猫玩偶的售价x 元,则每个A 款熊猫玩偶的售价
由题意得 · ……… …………………2分
解得:x=25 … …… ………3分
经检验,x=25 是原方程的解,且符合题意, ……………………………4分
答:每台 B 款电器的售价为25元.
(2)每个A 款熊猫玩偶应降价m 元,
由题意得(16-m)( , …………………………5分
整理得:m -6m+40=0,
解得:m=10,mz=-4,……………………………7 分
∵为了尽快减少库存,
∴m=10.
答:每个A 款熊猫玩偶应降价10元.………………………………8分
(备注:第(2)中解正确但没有舍根的情况,只扣1分;设未知数的表述、未作答或答的
表述不规范的情况,扣1分)
20.证明:(1)四边形 ABCD是菱形
∵AB=BC,BO 平分∠ABC,
∴AC⊥BD,AO=CO.
∵AD//BE,
∴∠ADO=∠CBO
∴△ADO ≌ △CBO(AAS) ……………………………………………………2分
∴AD=BC
∴四边形 ABCD 是平行四边形.…………………………3分
∵AB=BC,
∴四边形 ABCD 是菱形.……………4 分
解:(2)∵OC//DE,O 是 BD的中点,
5.……………………………5分
∵AD//BE,
∴∠DAO=∠BCO
设 BO=X,则 BC=√5X.
……………………………6分
由RT△BOC得,X +5 =(√5x)
(
…………
……………………7
分
)·
:
即
(
是菱形
)∵四边形 ABCD
∴BD=2BO=5,AC=2CO=10
5… ……… ……………………8分
(备注:第(1)按步骤给分即可;第(2)问方法较多,按照步骤给分。)
21解:(1) m ………… ………2分
解:(2)由题意得: CDIAM,BDⅡAE,∠C=∠CAM=90°,
∵CDⅡAM,
∴∠CDA=∠DAM=β,
∵BDⅡAE,
∴∠BDA=∠EAD,
∴∠CDA-∠BDA=∠DAM-∠EAD,
∴∠CDB=∠EAM=a
在RT△CBD中,∠C=90°,
∴设 BC=x,CD=3x.
在RT△ACD 中,∠C=90°,
……… … … 3分
……4分
解得
. ………………5分
(备注:最后一步写错一个答案扣1分。)
解:(3)①由F 为抛物线顶点,可知FC=FD,
∵∠CFD=90°,
∴△FCD 为等腰直角三角形.
由二次函数对称性可知, F(1,1)
(
设二次函数为
y
=ax(x-2),
代入
F(1,1)
得
1=a(-1),
解得
a=-
1
∴y
关于
x
的关系式为:
y
=-x(x-2)=-x +2x
6
分
)
②BD '光线与水平方向的夹角为0,过 D'作x 轴的垂线交x 轴于点 E,
过日作y轴的重线,两条理线交于点H即
设 D'H=2m,BH=3m, 则点D(3m, ),……………………………7分
代入y=-x(x-2) 得 化简得27m -12m-2=0
解得, (答案不合理,舍去)……………………………8分
∴遮阳蓬点 D 上升的高度最小值为(… ……………………9分
22.(1) ① 90° ;……………………………1分
证明:②由旋转的性质可知,∠HDG=∠HAD
∵∠AHD=∠DHG,
∴△HDG~△HAD ………………………………3分
解:(2)∵AC=4,BC=3,
由勾股定理得,AC= √3 +4 =5,
∵△DEF的锐角顶点 D 恰好落在△ABC的斜边AB上,
∴AG=DG=GC,A、D、C 在以G 为圆心AG为半径的圆上.
∴∠ADC=90°
………
∵△HDG~△HAD
……………4分
设GH=5x, 则DH=8x,AH=5x+2
解得 经检验, 是方程的解……………………………5分
………
……6分
(3) 和 …… …10分(备注:对1个答案给2分。)
同课章节目录
