数学:第二章《函数》课件(新人教b版必修1)
文档属性
| 名称 | 数学:第二章《函数》课件(新人教b版必修1) |  | |
| 格式 | rar | ||
| 文件大小 | 247.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-21 07:00:00 | ||
图片预览






文档简介
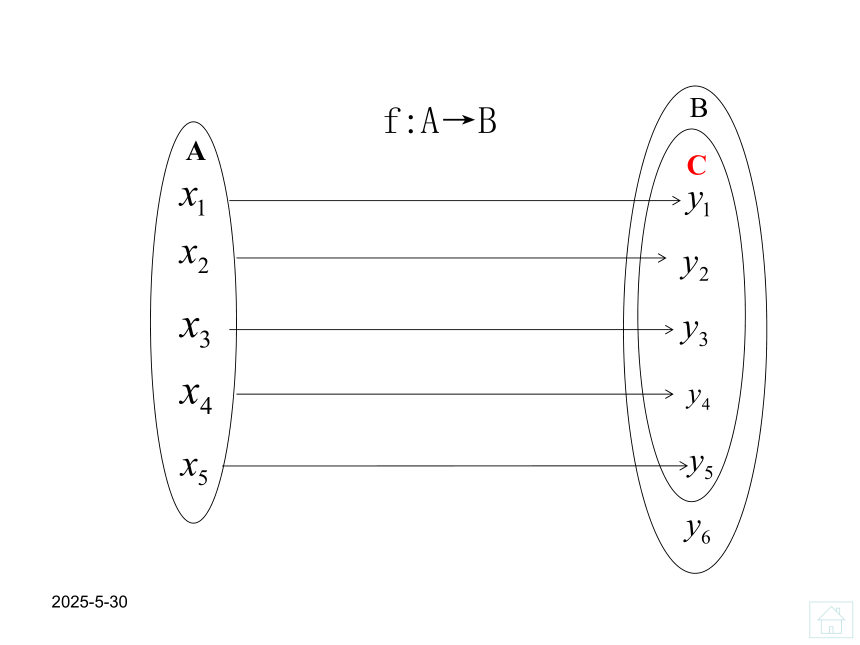
课件16张PPT。必修1 函数复习 课件2019-3-13定义域图象反函数值域单调性一次函数指数函数对数函数函数的复习主要抓住两条主线1、函数的概念及其有关性质。2、几种基本函数的具体性质。二次函数反比例函数解析式函数函数的概念 A、B是两个非空的集合,如果按某
个确定的对应关系f,使对于集合A中的
任意一个数x,在集合B中都有唯一的数
f(x)和它对应,那么就称f:A→B为从集
合A到集合B的一个函数。记作 y=f(x)
x∈A。其中,x叫做自变量,x的取值范
围A叫做函数的定义域;与x的值相对应
的y的值叫做函数值,函数值的集合
{f(x)│x ∈A}叫做函数的值域。
函数的三要素:定义域,值域,对应法则。2019-3-13Bf:A→B2019-3-13使函数有意义的x的取值范围。1、分式的分母不为零。
2、偶次方根的被开方数不小于零。
3、零次幂的底数不为零。函数定义域已知函数解析式求定义域主要依据抽象函数求定义域实际问题中函数的定义域2019-3-13求值域的一些方法: 1、观察法。
2、反函数法。
3、配方法。
4、换元法。
5、判别式法。
6 、数形结合法。
7 、函数单调性法。
2019-3-13求函数解析式的方法:1 、待定系数法。2 、换元法。4、解方程组消去法。3 、配凑法。2019-3-131、用描点法画图。2、用某种函数的图象变换而成。(1)、平移变换。(2) 、对称变换。函数的图象(3) 、翻折变换。2019-3-13函数的单调性 一般地,设函数y=f(x)的定义域为A ,
区间M A。如果取区间M中的任意两个
值 , , ,则当
那么就说f (x)在这个区间上是增函数。 一般地,设函数y=f(x)的定义域为A ,
区间M A。如果取区间M中的任意两个
值 , , ,则当
那么就说f (x)在这个区间上是减函数。2019-3-131、反函数存在的判定。2、求反函数的步骤.1)互换性:反函数的定义域是原函数的值域。反函数的值域是原函数的定义域。反函数的图象与原函数的图象关于
直线 y = x 对称。反函数的内容3、互为反函数间的关系:2)对称性:3)单调性:若原函数单调,则反函数也单调,
且增减性与原函数同。 4)两等式:2019-3-13一次函数y=ax+b (a 0)a>0a<01.图象oxyoxy2.定义域RR3.值域4.单调性在R上是增函数在R上是减函数2019-3-13二次函数a>0a<0xxyyoo1.图象2.定义域 R3.值域4.对称轴5.单调性2019-3-13反比例函数k>0k<01.图象2.定义域3.值域5.单调性4.对称中心原点(0,0)oxyoxy2019-3-131.指出求下列函数解析式的方法。2, 已知f(x)是一次函数,且f[f(x)]=4x+3求f(x).4, 已知 f(x)+2f(-x)=3x+2 求f(x).2019-3-13小结:本节课的主要收获不在于完成了多少道题,而在于增强了学生的整理意识,锻炼了学生归纳整理的能力。
?
2019-3-13作业:1)? 各组同学归纳出了本部分知识的框架,
还需深入整理,课后整理好。
2)函数问题不仅是知识点,概念性质问题,
还有常用的思想方法等问题,课后归纳整
理。
2019-3-13
个确定的对应关系f,使对于集合A中的
任意一个数x,在集合B中都有唯一的数
f(x)和它对应,那么就称f:A→B为从集
合A到集合B的一个函数。记作 y=f(x)
x∈A。其中,x叫做自变量,x的取值范
围A叫做函数的定义域;与x的值相对应
的y的值叫做函数值,函数值的集合
{f(x)│x ∈A}叫做函数的值域。
函数的三要素:定义域,值域,对应法则。2019-3-13Bf:A→B2019-3-13使函数有意义的x的取值范围。1、分式的分母不为零。
2、偶次方根的被开方数不小于零。
3、零次幂的底数不为零。函数定义域已知函数解析式求定义域主要依据抽象函数求定义域实际问题中函数的定义域2019-3-13求值域的一些方法: 1、观察法。
2、反函数法。
3、配方法。
4、换元法。
5、判别式法。
6 、数形结合法。
7 、函数单调性法。
2019-3-13求函数解析式的方法:1 、待定系数法。2 、换元法。4、解方程组消去法。3 、配凑法。2019-3-131、用描点法画图。2、用某种函数的图象变换而成。(1)、平移变换。(2) 、对称变换。函数的图象(3) 、翻折变换。2019-3-13函数的单调性 一般地,设函数y=f(x)的定义域为A ,
区间M A。如果取区间M中的任意两个
值 , , ,则当
那么就说f (x)在这个区间上是增函数。 一般地,设函数y=f(x)的定义域为A ,
区间M A。如果取区间M中的任意两个
值 , , ,则当
那么就说f (x)在这个区间上是减函数。2019-3-131、反函数存在的判定。2、求反函数的步骤.1)互换性:反函数的定义域是原函数的值域。反函数的值域是原函数的定义域。反函数的图象与原函数的图象关于
直线 y = x 对称。反函数的内容3、互为反函数间的关系:2)对称性:3)单调性:若原函数单调,则反函数也单调,
且增减性与原函数同。 4)两等式:2019-3-13一次函数y=ax+b (a 0)a>0a<01.图象oxyoxy2.定义域RR3.值域4.单调性在R上是增函数在R上是减函数2019-3-13二次函数a>0a<0xxyyoo1.图象2.定义域 R3.值域4.对称轴5.单调性2019-3-13反比例函数k>0k<01.图象2.定义域3.值域5.单调性4.对称中心原点(0,0)oxyoxy2019-3-131.指出求下列函数解析式的方法。2, 已知f(x)是一次函数,且f[f(x)]=4x+3求f(x).4, 已知 f(x)+2f(-x)=3x+2 求f(x).2019-3-13小结:本节课的主要收获不在于完成了多少道题,而在于增强了学生的整理意识,锻炼了学生归纳整理的能力。
?
2019-3-13作业:1)? 各组同学归纳出了本部分知识的框架,
还需深入整理,课后整理好。
2)函数问题不仅是知识点,概念性质问题,
还有常用的思想方法等问题,课后归纳整
理。
2019-3-13
