2024年深圳市宝安第一外国语学校初三数学5月月考试卷(pdf版无答案)
文档属性
| 名称 | 2024年深圳市宝安第一外国语学校初三数学5月月考试卷(pdf版无答案) |  | |
| 格式 | |||
| 文件大小 | 475.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-02 14:55:44 | ||
图片预览



文档简介
初三年级 5 月数学学科学情反馈
一、选择题(共 10 小题,每小题 3 分,共 30 分)
1.有理数这个概念最早源自《几何原本》,以下各数中,有理数为( )
A. 1 B. 2 C. π D. 2.024002400024
9
2. 下列英文字母中,为中心对称图形的是( )
A. B. C. D.
3. 2024年春节前夕,全国多地、多趟列车受冰雪天气影响,“春运”第 70年见证
了“高铁速度,绿皮温度”,据统计,全国铁路春运期间发送旅客 4.8亿人次,
数据 4.8亿用科学计数法表示正确的是( )
A. 4.8 1010 B. 4.8 109 C. 48 108 D. 4.8 108
4. 下列运算正确的是( )
A. a2 a2 a4 B. a2 a C. a2 a2 a4 D. a8 a4 a2
5. 如图是某家具店出售的黄色木椅的侧面图,其中∠ABD =130°,CD∥EF,∠E
= 60°,则∠BDC =( )
A. 70° B. 60° C. 50° D. 40°
第 6题
第 5题
6. 数学的应用无处不在,如图,某机场的告示牌中,提示随身携带行李的规则,
其中提到每件行李重量限制“≤8千克”,则将表示行李限额的不等式表示在数
轴上为( )
A. B.
第 1 页 共 8 页
C. D.
7. 为纪念北京奥运会成功举办,国务院批准从 2009年起,将每年 8月 8日设置
为“全民健身日”。因为为了认真发展体育运动,增强人民体质,贯彻执行《中华
人民共和国体育法》,网上各种健身项目层出不穷。如图是侧抬腿运动,可以保
证全身得到锻炼!已知小敏大腿根部距脚尖 90cm,即 OA=90cm,当其完成图中
一次动作时,脚尖划过的轨迹长度为( )cm.
45
A. B.
45 C. 45 D. 45
2 4 2
8. 以下说法正确的是( )
A. 1若分式 有意义,则 x 3
x 3
B.将抛物线 y 3x2向左平移 1个单位,得到抛物线 y (3 x 1)2 的图象
C. 2对于反比例函数 y ,y随 x的增大而减小
x
D. 到三角形三边距离相等的点是三边角平分线的交点
9.山西刀削面作为国家级非遗美食,吸引了大批游客品尝!为了更好地传承这种
非遗美食,同时解放人的双手,某公司推出了一款刀削面机器人,宣传标语如下:
机器化时代,帮您解决一切人工问题!
速度更快:每台削面机器人比一个削面师傅每分
钟多削 160刀!
效率更高:每台削面机器人削 660刀的时间和一
个削面师傅削 180刀的时间相同!
机器铸造未来,让生活美美的偷个懒!
第 2 页 共 8 页
根据该宣传,求每台削面机器人每分钟能削多少刀面.设每台削面机器人每分钟
能削 x刀面,根据题意可列方程为( )
660 180 B. 660 180 C. 660 180 D. 660 180
A. x x 160 x 160 x x 160 x x x 160
10. 如图,动点 P、Q在平行四边形 ABCD的边和对角线上运动,动点 P的运动
轨迹为折线 O-A-D-O,动点 Q的运动轨迹为折线 O-C-B-O,两动点同时开始运
动,且运动速度均为 1 cm/s. 设动点运动时间为 x秒,两动点间距离为 y cm,x
与 y的函数关系式如图所示. 当点 P在平行四边形 ABCD的边上运动时,两动点
3
间的最短距离为 m,此时运动时间为( 3 )秒,则 m的值为( ).
2
A. 3 B. 3 C. 3 3 D. 3
2 2 2
二、填空题(共 5 小题,每小题 3 分,共 15 分) 14 题图②
11. 因式分解: x3 4x _____▲__________.
12. 若一元二次方程 x2 5x m 0有两个不相等的实数根,则满足条件的正整数
m的值为 ▲ .(只需要填一个)
13. 化学课上,同学们将元素周期表中的前 5位化学元素(氢氦锂铍硼)制成了
一副互不重复的元素扑克牌(共 5张,每张上记录一种化学元素). 小明从中先
任意抽取一张记录下来,不放回,然后再从中抽取一张记录,则小明两次抽到的
元素中含稀有气体的概率为__▲_____.
14. 一束光从空气中以不同的角度摄入水中,会发生反射和
图②
图② 折射现象,如图①是光束在空水中的径迹. 如图②,现将一
4
束光以一定的入射角 (tan = )射入水面 GK,此时反射
3
光线与折射光线夹角恰为90 ,直线 l为法线,若水深为 3m,
图①
则线段 CD =___▲_____m.
第 3 页 共 8 页
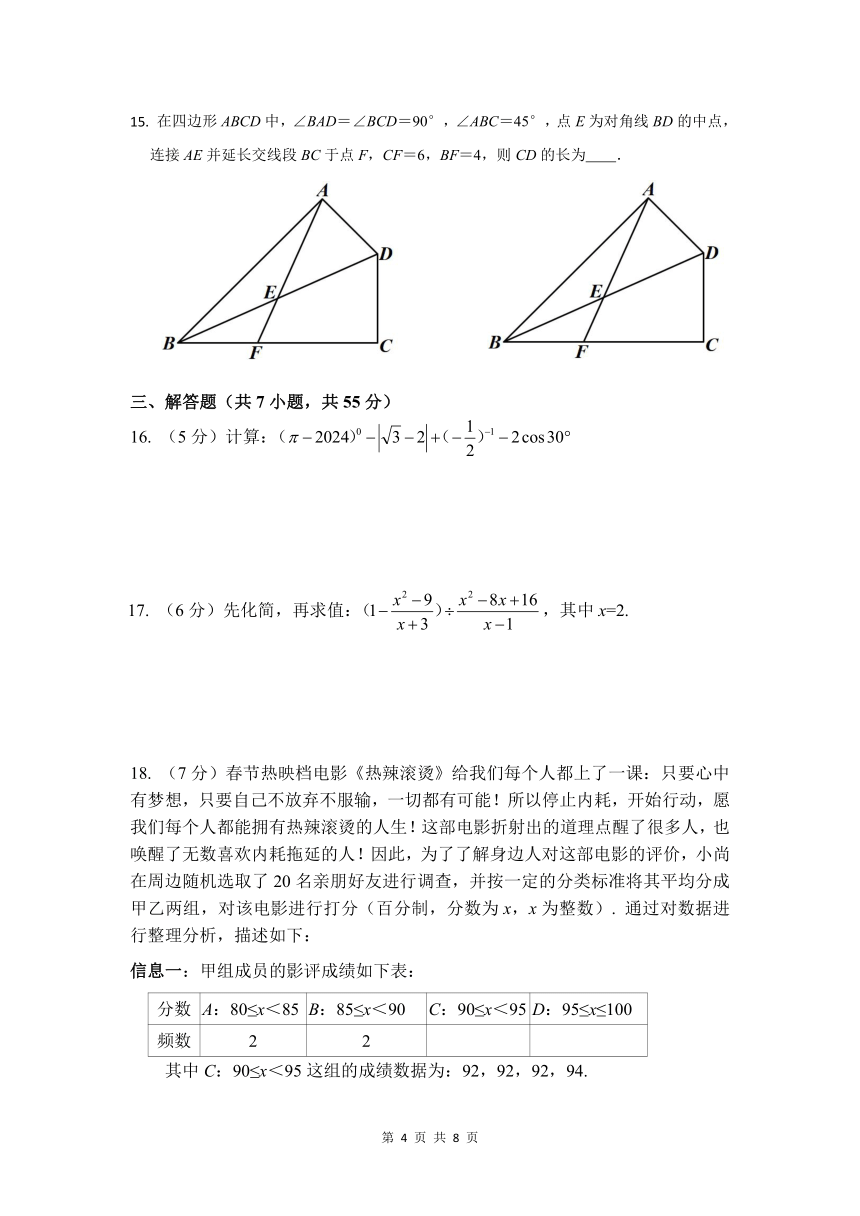
15. 在四边形 ABCD中,∠BAD=∠BCD=90°,∠ABC=45°,点 E为对角线 BD的中点,
连接 AE并延长交线段 BC于点 F,CF=6,BF=4,则 CD的长为 .
三、解答题(共 7 小题,共 55 分)
16. (5 1分)计算:( 2024)0 3 2 ( ) 1 2cos30
2
2 2
17. 6 1 x 9 x 8x 16( 分)先化简,再求值:( ) ,其中 x=2.
x 3 x 1
18. (7分)春节热映档电影《热辣滚烫》给我们每个人都上了一课:只要心中
有梦想,只要自己不放弃不服输,一切都有可能!所以停止内耗,开始行动,愿
我们每个人都能拥有热辣滚烫的人生!这部电影折射出的道理点醒了很多人,也
唤醒了无数喜欢内耗拖延的人!因此,为了了解身边人对这部电影的评价,小尚
在周边随机选取了 20名亲朋好友进行调查,并按一定的分类标准将其平均分成
甲乙两组,对该电影进行打分(百分制,分数为 x,x为整数). 通过对数据进
行整理分析,描述如下:
信息一:甲组成员的影评成绩如下表:
分数 A:80≤x<85 B:85≤x<90 C:90≤x<95 D:95≤x≤100
频数 2 2
其中 C:90≤x<95这组的成绩数据为:92,92,92,94.
第 4 页 共 8 页
信息二:乙组成员的影评成绩分布见如下扇形统计图:
其中在 C:90≤x<95这组的成绩数据为:93,93,93.
信息三: 组号 平均数 众数 中位数
甲 90.6 m n
乙 92.3 100 93
根据以上提供的三个信息,回答下列问题:
(1)m =___▲____,n =____▲____,a =___▲_____;
(2)影评分数在 D:95≤x<100区间的视为“电影铁粉”,若乙组中共有 200人参
与此次影评活动,则乙组中有__▲____人为“电影铁粉”.
(3)由于甲组成员不掺杂粉丝膜拜心理,仅仅针对电影内容做出评价,故评价
更为客观. 现将甲乙两组平均数按 7:3 的比例进行加权,得到此次影评的最终
成绩为___▲____.
19. (8分)投壶是中国古代的一种弓箭投掷游戏,弓箭投入壶内、壶耳会得到不同的分数,
落在地上不得分.小龙与小华每人拿 10支箭进行游戏,游戏结果如下:
投入壶内 投入壶耳 落在地上 总分
小龙 3支 4支 3支 27分
小华 3支 3支 4支 24分
(1)求一支弓箭投入壶内、壶耳各得几分?
(2)小丽也加入游戏,投完 10支箭后,有 2支弓箭落到了地上,若小丽赢得
了比赛,则她至少投入壶内几支箭?
第 5 页 共 8 页
20. (9分)如图,以平行四边形 ABCD的一边 AB为直径的圆交边 BC于点 E,
交对角线 AC于点 F,G是边 CD上的一点,连接 AG,且 BE=DG .
(1)请在以下三个条件中任选一个: ▲ ,证明:直线 AG是圆 M的切线.
①∠AGD =∠ACB;②F是弧 AE的中点;③E是 BC的中点.
(2)在第(1)问的条件下,若直径为 4,连接
BF并延长交 AG于点 N,AN =3,求四边形 ABCD
的面积.
第 6 页 共 8 页
21. (10分)根据以下素材,探索完成任务.
如何设计拱桥景观灯的悬挂方案?
素材 1 图 1中有一座拱桥,图 2
是其抛物线形桥拱的示
意图,某时测得水面宽
20m,拱顶离水面 5m.据
调查,该河段水位在此基
础上再涨1.8m达到最高.
素材 2 为迎佳节,拟在图 1桥洞
前面的桥拱上悬挂 40cm
长的灯笼,如图 3.为了
安全,灯笼底部距离水面
不小于 1m;为了实效,
相邻两盏灯笼悬挂点的
水平间距均为 1.6m;为了
美观,要求在符合条件处
都挂上灯笼,且挂满后成
轴对称分布.
问题解决
任务 1 确定桥拱 在图 2中建立合适的直角坐标系,求抛物线的函数表达式.
形状
任务 2 探究悬挂 在你所建立的坐标系中,仅在安全的条件下,确定可悬挂点的纵坐标
范围 的最小值和横坐标的取值范围.
任务 3 拟定设计 给出一种符合所有悬挂条件的灯笼数量:_______,并根据你所建立
方案 的坐标系,求出最左边一盏灯笼悬挂点的横坐标:_______.
第 7 页 共 8 页
22. (10分)剪纸在中国是历史悠久,并且流传很广的一种民间艺术形式。剪纸
虽然制作简便,造型单纯,但由于其能够充分反映百姓的生活内涵,具有浓郁的
民俗特色,因此是中国众多民间美术形式的浓缩与夸张。学完全等和相似以后,
一个小组的同学拿着一张边长为5的正方形纸片,在BC边上取一点E,使得CE=2,
过点 E所在直线剪掉一个直角三角形,点 E所在直线交 CD于点 F,过点 F所在
直线再剪掉一个直角三角形,使得剪掉的两个三角形全等.
甲同学认为只有一种剪法; 乙同学认为有两种剪法; 丙同学认为有三种剪法
(1)你认为哪位同学的说法是正确的 (填“甲”或“乙”或“丙”),请在下图
中画出一种正确的画法,并直接写出所画图中 CF的长度__________.
(备用图)
(2)按照上面的条件,使剪掉的两个直角三角形相似(点 F不与 D重合),过
点 F所在直线交 AD于点 G,设 CF = x, DG = y.
①求出 y与 x的函数关系式;②当 DG最大时,则 tan∠BFE=_______.
(3)将一张矩形纸片 ABMN(AB<BM),先沿一条直线剪掉一个直角三角形,
在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角
形相似),剩下的是如图所示的四边形纸片 ABCD;其中∠A=90°,AB=24,
BC=20,CD=15,AD=7,则 AN= .(画出示意图)
(备用图)
第 8 页 共 8 页
一、选择题(共 10 小题,每小题 3 分,共 30 分)
1.有理数这个概念最早源自《几何原本》,以下各数中,有理数为( )
A. 1 B. 2 C. π D. 2.024002400024
9
2. 下列英文字母中,为中心对称图形的是( )
A. B. C. D.
3. 2024年春节前夕,全国多地、多趟列车受冰雪天气影响,“春运”第 70年见证
了“高铁速度,绿皮温度”,据统计,全国铁路春运期间发送旅客 4.8亿人次,
数据 4.8亿用科学计数法表示正确的是( )
A. 4.8 1010 B. 4.8 109 C. 48 108 D. 4.8 108
4. 下列运算正确的是( )
A. a2 a2 a4 B. a2 a C. a2 a2 a4 D. a8 a4 a2
5. 如图是某家具店出售的黄色木椅的侧面图,其中∠ABD =130°,CD∥EF,∠E
= 60°,则∠BDC =( )
A. 70° B. 60° C. 50° D. 40°
第 6题
第 5题
6. 数学的应用无处不在,如图,某机场的告示牌中,提示随身携带行李的规则,
其中提到每件行李重量限制“≤8千克”,则将表示行李限额的不等式表示在数
轴上为( )
A. B.
第 1 页 共 8 页
C. D.
7. 为纪念北京奥运会成功举办,国务院批准从 2009年起,将每年 8月 8日设置
为“全民健身日”。因为为了认真发展体育运动,增强人民体质,贯彻执行《中华
人民共和国体育法》,网上各种健身项目层出不穷。如图是侧抬腿运动,可以保
证全身得到锻炼!已知小敏大腿根部距脚尖 90cm,即 OA=90cm,当其完成图中
一次动作时,脚尖划过的轨迹长度为( )cm.
45
A. B.
45 C. 45 D. 45
2 4 2
8. 以下说法正确的是( )
A. 1若分式 有意义,则 x 3
x 3
B.将抛物线 y 3x2向左平移 1个单位,得到抛物线 y (3 x 1)2 的图象
C. 2对于反比例函数 y ,y随 x的增大而减小
x
D. 到三角形三边距离相等的点是三边角平分线的交点
9.山西刀削面作为国家级非遗美食,吸引了大批游客品尝!为了更好地传承这种
非遗美食,同时解放人的双手,某公司推出了一款刀削面机器人,宣传标语如下:
机器化时代,帮您解决一切人工问题!
速度更快:每台削面机器人比一个削面师傅每分
钟多削 160刀!
效率更高:每台削面机器人削 660刀的时间和一
个削面师傅削 180刀的时间相同!
机器铸造未来,让生活美美的偷个懒!
第 2 页 共 8 页
根据该宣传,求每台削面机器人每分钟能削多少刀面.设每台削面机器人每分钟
能削 x刀面,根据题意可列方程为( )
660 180 B. 660 180 C. 660 180 D. 660 180
A. x x 160 x 160 x x 160 x x x 160
10. 如图,动点 P、Q在平行四边形 ABCD的边和对角线上运动,动点 P的运动
轨迹为折线 O-A-D-O,动点 Q的运动轨迹为折线 O-C-B-O,两动点同时开始运
动,且运动速度均为 1 cm/s. 设动点运动时间为 x秒,两动点间距离为 y cm,x
与 y的函数关系式如图所示. 当点 P在平行四边形 ABCD的边上运动时,两动点
3
间的最短距离为 m,此时运动时间为( 3 )秒,则 m的值为( ).
2
A. 3 B. 3 C. 3 3 D. 3
2 2 2
二、填空题(共 5 小题,每小题 3 分,共 15 分) 14 题图②
11. 因式分解: x3 4x _____▲__________.
12. 若一元二次方程 x2 5x m 0有两个不相等的实数根,则满足条件的正整数
m的值为 ▲ .(只需要填一个)
13. 化学课上,同学们将元素周期表中的前 5位化学元素(氢氦锂铍硼)制成了
一副互不重复的元素扑克牌(共 5张,每张上记录一种化学元素). 小明从中先
任意抽取一张记录下来,不放回,然后再从中抽取一张记录,则小明两次抽到的
元素中含稀有气体的概率为__▲_____.
14. 一束光从空气中以不同的角度摄入水中,会发生反射和
图②
图② 折射现象,如图①是光束在空水中的径迹. 如图②,现将一
4
束光以一定的入射角 (tan = )射入水面 GK,此时反射
3
光线与折射光线夹角恰为90 ,直线 l为法线,若水深为 3m,
图①
则线段 CD =___▲_____m.
第 3 页 共 8 页
15. 在四边形 ABCD中,∠BAD=∠BCD=90°,∠ABC=45°,点 E为对角线 BD的中点,
连接 AE并延长交线段 BC于点 F,CF=6,BF=4,则 CD的长为 .
三、解答题(共 7 小题,共 55 分)
16. (5 1分)计算:( 2024)0 3 2 ( ) 1 2cos30
2
2 2
17. 6 1 x 9 x 8x 16( 分)先化简,再求值:( ) ,其中 x=2.
x 3 x 1
18. (7分)春节热映档电影《热辣滚烫》给我们每个人都上了一课:只要心中
有梦想,只要自己不放弃不服输,一切都有可能!所以停止内耗,开始行动,愿
我们每个人都能拥有热辣滚烫的人生!这部电影折射出的道理点醒了很多人,也
唤醒了无数喜欢内耗拖延的人!因此,为了了解身边人对这部电影的评价,小尚
在周边随机选取了 20名亲朋好友进行调查,并按一定的分类标准将其平均分成
甲乙两组,对该电影进行打分(百分制,分数为 x,x为整数). 通过对数据进
行整理分析,描述如下:
信息一:甲组成员的影评成绩如下表:
分数 A:80≤x<85 B:85≤x<90 C:90≤x<95 D:95≤x≤100
频数 2 2
其中 C:90≤x<95这组的成绩数据为:92,92,92,94.
第 4 页 共 8 页
信息二:乙组成员的影评成绩分布见如下扇形统计图:
其中在 C:90≤x<95这组的成绩数据为:93,93,93.
信息三: 组号 平均数 众数 中位数
甲 90.6 m n
乙 92.3 100 93
根据以上提供的三个信息,回答下列问题:
(1)m =___▲____,n =____▲____,a =___▲_____;
(2)影评分数在 D:95≤x<100区间的视为“电影铁粉”,若乙组中共有 200人参
与此次影评活动,则乙组中有__▲____人为“电影铁粉”.
(3)由于甲组成员不掺杂粉丝膜拜心理,仅仅针对电影内容做出评价,故评价
更为客观. 现将甲乙两组平均数按 7:3 的比例进行加权,得到此次影评的最终
成绩为___▲____.
19. (8分)投壶是中国古代的一种弓箭投掷游戏,弓箭投入壶内、壶耳会得到不同的分数,
落在地上不得分.小龙与小华每人拿 10支箭进行游戏,游戏结果如下:
投入壶内 投入壶耳 落在地上 总分
小龙 3支 4支 3支 27分
小华 3支 3支 4支 24分
(1)求一支弓箭投入壶内、壶耳各得几分?
(2)小丽也加入游戏,投完 10支箭后,有 2支弓箭落到了地上,若小丽赢得
了比赛,则她至少投入壶内几支箭?
第 5 页 共 8 页
20. (9分)如图,以平行四边形 ABCD的一边 AB为直径的圆交边 BC于点 E,
交对角线 AC于点 F,G是边 CD上的一点,连接 AG,且 BE=DG .
(1)请在以下三个条件中任选一个: ▲ ,证明:直线 AG是圆 M的切线.
①∠AGD =∠ACB;②F是弧 AE的中点;③E是 BC的中点.
(2)在第(1)问的条件下,若直径为 4,连接
BF并延长交 AG于点 N,AN =3,求四边形 ABCD
的面积.
第 6 页 共 8 页
21. (10分)根据以下素材,探索完成任务.
如何设计拱桥景观灯的悬挂方案?
素材 1 图 1中有一座拱桥,图 2
是其抛物线形桥拱的示
意图,某时测得水面宽
20m,拱顶离水面 5m.据
调查,该河段水位在此基
础上再涨1.8m达到最高.
素材 2 为迎佳节,拟在图 1桥洞
前面的桥拱上悬挂 40cm
长的灯笼,如图 3.为了
安全,灯笼底部距离水面
不小于 1m;为了实效,
相邻两盏灯笼悬挂点的
水平间距均为 1.6m;为了
美观,要求在符合条件处
都挂上灯笼,且挂满后成
轴对称分布.
问题解决
任务 1 确定桥拱 在图 2中建立合适的直角坐标系,求抛物线的函数表达式.
形状
任务 2 探究悬挂 在你所建立的坐标系中,仅在安全的条件下,确定可悬挂点的纵坐标
范围 的最小值和横坐标的取值范围.
任务 3 拟定设计 给出一种符合所有悬挂条件的灯笼数量:_______,并根据你所建立
方案 的坐标系,求出最左边一盏灯笼悬挂点的横坐标:_______.
第 7 页 共 8 页
22. (10分)剪纸在中国是历史悠久,并且流传很广的一种民间艺术形式。剪纸
虽然制作简便,造型单纯,但由于其能够充分反映百姓的生活内涵,具有浓郁的
民俗特色,因此是中国众多民间美术形式的浓缩与夸张。学完全等和相似以后,
一个小组的同学拿着一张边长为5的正方形纸片,在BC边上取一点E,使得CE=2,
过点 E所在直线剪掉一个直角三角形,点 E所在直线交 CD于点 F,过点 F所在
直线再剪掉一个直角三角形,使得剪掉的两个三角形全等.
甲同学认为只有一种剪法; 乙同学认为有两种剪法; 丙同学认为有三种剪法
(1)你认为哪位同学的说法是正确的 (填“甲”或“乙”或“丙”),请在下图
中画出一种正确的画法,并直接写出所画图中 CF的长度__________.
(备用图)
(2)按照上面的条件,使剪掉的两个直角三角形相似(点 F不与 D重合),过
点 F所在直线交 AD于点 G,设 CF = x, DG = y.
①求出 y与 x的函数关系式;②当 DG最大时,则 tan∠BFE=_______.
(3)将一张矩形纸片 ABMN(AB<BM),先沿一条直线剪掉一个直角三角形,
在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角
形相似),剩下的是如图所示的四边形纸片 ABCD;其中∠A=90°,AB=24,
BC=20,CD=15,AD=7,则 AN= .(画出示意图)
(备用图)
第 8 页 共 8 页
同课章节目录
