期中评估测试卷(含答案) 2024-2025学年数学北师大版九年级下册
文档属性
| 名称 | 期中评估测试卷(含答案) 2024-2025学年数学北师大版九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 261.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 21:28:16 | ||
图片预览



文档简介
期中评估测试卷
(满分:120分 时间:120分钟)
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图,在4×4的正方形网格中,tan α的值为 ( )
A. B.2 C. D.
2.已知y=(m+1)+2x-3是二次函数,则m的值为 ( )
A.0 B.1 C.-1 D.1或-1
3.在平面直角坐标系xOy中,抛物线的顶点是(1,3),当x>1时,y随x的增大而增大,则抛物线表达式可以是 ( )
A.y=-2(x+1)2+3 B.y=2(x+1)2+3
C.y=-2(x-1)2+3 D.y=2(x-1)2+3
4.抛物线y=-(x+3)(x-2)与x轴的两交点之间的距离是 ( )
A.1 B.3 C.5 D.6
5.在Rt△ABC中,∠C=90°,若sin A=,则cos A的值为 ( )
A. B. C. D.
6.如图1是莲花山景区一座抛物线形拱桥,按图2所示建立平面直角坐标系,得到抛物线表达式为y=-x2,正常水位时水面宽AB为36 m,当水位上升5 m时水面宽CD为 ( )
图1 图2
A.10 m B.12 m C.24 m D.48 m
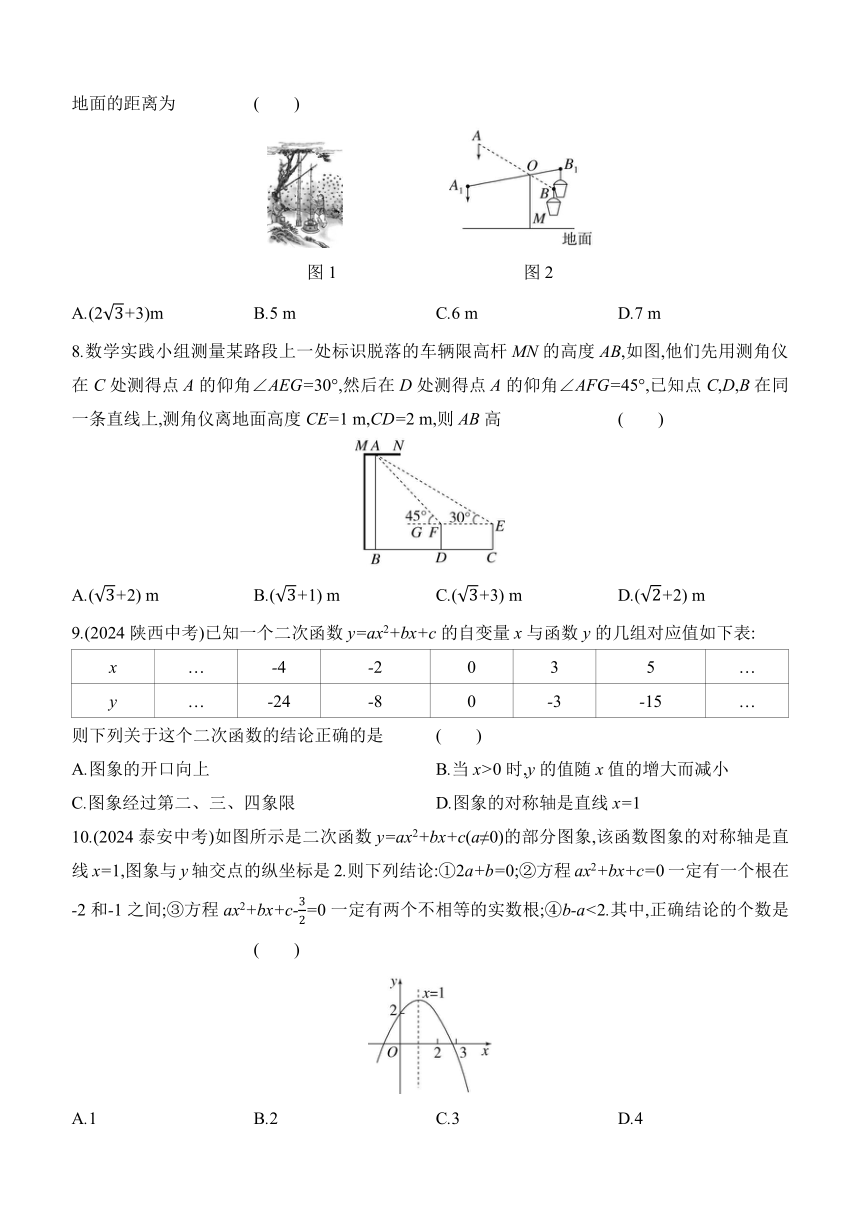
7.(2024深圳龙岗区模拟)桔槔俗称“吊杆”“称杆”(如图1),是我国古代农用工具,始见于《墨子·备城门》,是一种利用杠杆原理的取水机械.桔槔示意图如图2所示,OM是垂直于水平地面的支撑杆,OM=3 m,AB是杠杆,AB=6 m,OA∶OB=2∶1.当点A位于最高点时,∠AOM=120°.此时,点A到地面的距离为 ( )
图1 图2
A.(2+3)m B.5 m C.6 m D.7 m
8.数学实践小组测量某路段上一处标识脱落的车辆限高杆MN的高度AB,如图,他们先用测角仪在C处测得点A的仰角∠AEG=30°,然后在D处测得点A的仰角∠AFG=45°,已知点C,D,B在同一条直线上,测角仪离地面高度CE=1 m,CD=2 m,则AB高 ( )
A.(+2) m B.(+1) m C.(+3) m D.(+2) m
9.(2024陕西中考)已知一个二次函数y=ax2+bx+c的自变量x与函数y的几组对应值如下表:
x … -4 -2 0 3 5 …
y … -24 -8 0 -3 -15 …
则下列关于这个二次函数的结论正确的是 ( )
A.图象的开口向上 B.当x>0时,y的值随x值的增大而减小
C.图象经过第二、三、四象限 D.图象的对称轴是直线x=1
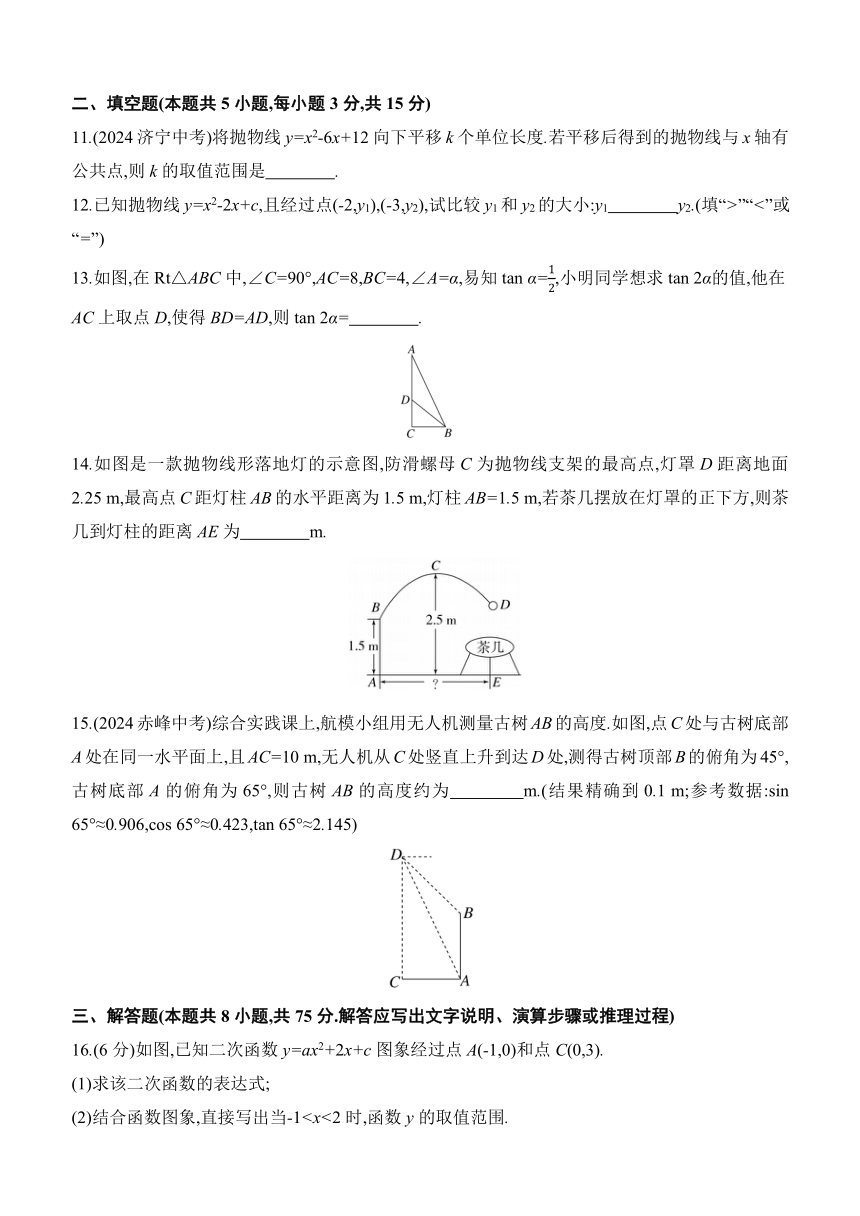
10.(2024泰安中考)如图所示是二次函数y=ax2+bx+c(a≠0)的部分图象,该函数图象的对称轴是直线x=1,图象与y轴交点的纵坐标是2.则下列结论:①2a+b=0;②方程ax2+bx+c=0一定有一个根在-2和-1之间;③方程ax2+bx+c-=0一定有两个不相等的实数根;④b-a<2.其中,正确结论的个数是 ( )
A.1 B.2 C.3 D.4
二、填空题(本题共5小题,每小题3分,共15分)
11.(2024济宁中考)将抛物线y=x2-6x+12向下平移k个单位长度.若平移后得到的抛物线与x轴有公共点,则k的取值范围是 .
12.已知抛物线y=x2-2x+c,且经过点(-2,y1),(-3,y2),试比较y1和y2的大小:y1 y2.(填“>”“<”或“=”)
13.如图,在Rt△ABC中,∠C=90°,AC=8,BC=4,∠A=α,易知tan α=,小明同学想求tan 2α的值,他在AC上取点D,使得BD=AD,则tan 2α= .
14.如图是一款抛物线形落地灯的示意图,防滑螺母C为抛物线支架的最高点,灯罩D距离地面2.25 m,最高点C距灯柱AB的水平距离为1.5 m,灯柱AB=1.5 m,若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为 m.
15.(2024赤峰中考)综合实践课上,航模小组用无人机测量古树AB的高度.如图,点C处与古树底部A处在同一水平面上,且AC=10 m,无人机从C处竖直上升到达D处,测得古树顶部B的俯角为45°,古树底部A的俯角为65°,则古树AB的高度约为 m.(结果精确到0.1 m;参考数据:sin 65°≈0.906,cos 65°≈0.423,tan 65°≈2.145)
三、解答题(本题共8小题,共75分.解答应写出文字说明、演算步骤或推理过程)
16.(6分)如图,已知二次函数y=ax2+2x+c图象经过点A(-1,0)和点C(0,3).
(1)求该二次函数的表达式;
(2)结合函数图象,直接写出当-117.(6分)如图,已知△ABD中,AC⊥BD,BC=8,CD=4,cos∠ABC=,BE为AD边上的中线.
(1)求AC的长;
(2)求△BED的面积.
18.(8分)某服装店销售一款卫衣,该款卫衣每件进价为60元,规定每件售价不低于进价.经市场调查发现,该款卫衣每月的销售量y(件)与每件售价x(元)满足一次函数关系y=-20x+2 400.
(1)若服装店每月既想从销售该款卫衣中获利16 000元,又想尽量给顾客实惠,售价应定为多少元
(2)为维护市场秩序,物价部门规定该款卫衣的每件利润不允许超过每件进价的40%.设该款卫衣每月的总利润为w(元),那么售价定为多少元时服装店可获得最大利润 最大利润是多少元
19.(10分)(2024广州中考)2024年6月2日,嫦娥六号着陆器和上升器组合体(简称为“着上组合体”)成功着陆在月球背面.某校综合实践小组制作了一个“着上组合体”的模拟装置,在一次试验中,如图,该模拟装置在缓速下降阶段从点A垂直下降到点B,再垂直下降到着陆点C,从点B测得地面点D的俯角为36.87°,AD=17 m,BD=10 m.
(1)求CD的长;
(2)若模拟装置从点A以每秒2 m的速度匀速下降到点B,求模拟装置从A点下降到点B的时间.
参考数据:sin 36.87°≈0.60,cos 36.87°≈0.80,tan 36.87°≈0.75.
20.(10分)(2024福建中考)如图,已知二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C,其中A(-2,0),C(0,-2).
(1)求二次函数的表达式;
(2)若P是二次函数图象上的一点,且点P在第二象限,线段PC交x轴于点D,△PDB的面积是
△CDB的面积的2倍,求点P的坐标.
21.(10分)如图,是一块抛物线形板材,工人师傅以A为坐标原点,AB边所在直线为x轴,过A点作AB的垂线为y轴,建立平面直角坐标系,根据测量得知AB边长为6 dm,最高点C到AB的距离为6 dm.
(1)求该抛物线的表达式.
(2)工人师傅计划在抛物线形板材上截出一个正方形CDEF,要求D,F两点在抛物线上(D在F的左侧),点E在抛物线的对称轴上,工人师傅的计划能否实现 若能,请你帮助工人师傅在抛物线上找出点D的位置(即求出点D的坐标),若不能,请说明理由.
22.(12分)(2024重庆B卷中考)如图,A,B,C,D分别是某公园四个景点,B在A的正东方向,D在A的正北方向,且在C的北偏西60°方向,C在A的北偏东30°方向,且在B的北偏西15°方向,AB=2 km.
(参考数据:≈1.41,≈1.73,≈2.45)
(1)求BC的长度(结果精确到0.1 km);
(2)甲、乙两人从景点D出发去景点B,甲选择的路线为:D-C-B,乙选择的路线为:D-A-B.请计算说明谁选择的路线较近
23.(13分)如图,在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象经过原点和点A(4,0).经过点A的直线与该二次函数图象交于点B(1,3),与y轴交于点C.
(1)求二次函数的表达式及点C的坐标;
(2)点P是二次函数图象上的一个动点,当点P在直线AB上方时,过点P作PE⊥x轴于点E,与直线AB交于点D,设点P的横坐标为m.
①m为何值时线段PD的长度最大,并求出最大值;
②是否存在点P,使得△BPD与△AOC相似.若存在,请求出点P坐标;若不存在,请说明理由.
【详解答案】
1.B 解析:由题图,tan α==2.故选B.
2.B 解析:由y=(m+1)+2x-3是二次函数,得,解得m=1.故选B.
3.D 解析:由题意得:抛物线的顶点是(1,3),开口向上.故选D.
4.C 解析:∵抛物线y=-(x+3)(x-2)与x轴有两个交点,∴-(x+3)(x-2)=0,解得:x1=-3,x2=2,
∴两个交点坐标是(-3,0),(2,0),∴两个交点之间的距离是5.故选C.
5.A 解析:∵在Rt△ABC中,∠C=90°,sin A=,∴设BC=5k,则AB=13k,根据勾股定理可以得到:AC==12k,∴cos A=.故选A.
6.C 解析:∵AB=36 m,∴当x=18时,y=-×182=-9,当水位上升5 m时,y=-4,把y=-4代入抛物线表达式得:-4=-x2,解得x=±12,此时水面宽CD=24(m).故选C.
7.B 解析:如图,过点O作EF⊥OM,过点A作AG⊥EF于点G,
∵AB=6 m,OA∶OB=2∶1,∴OA=4 m,∵∠AOM=120°,∠EOM=90°,∴∠AOE=30°,在Rt△AOG中,AG=AO·sin 30°=2(m),点A位于最高点时到地面的距离为2+3=5(m),∴点A到地面的距离为5 m.故选B.
8.A 解析:如图,延长EF交AB于点H,
由题意得,HB=DF=CE=1 m,CD=FE=2 m,设HF=x m,则EH=HF+FE=(x+2)m,在Rt△AHF中,∠AFH=45°,
∴∠FAH=45°,∴AH=HF=x m,在Rt△AHE中,tan 30°=,解得x=+1,
∴AB=AH+BH=+1+1=(+2)(m).故选A.
9.D 解析:由题知,解得∴二次函数的表达式为y=-x2+2x.∵a=-1<0,∴抛物线的开口向下.故A选项不符合题意.∵y=-x2+2x=-(x-1)2+1,∴当x>1时,y随x的增大而减小.故B选项不符合题意.令y=0得,-x2+2x=0,解得x1=0,x2=2,∴抛物线与x轴的交点坐标为(0,0)和(2,0).又∵抛物线的顶点坐标为(1,1),∴抛物线经过第一、三、四象限.故C选项不符合题意.∵二次函数表达式为y=-(x-1)2+1,∴抛物线的对称轴为直线x=1.故D选项符合题意.故选D.
10.B 解析:∵抛物线的对称轴为直线x=1,∴-=1,∴b=-2a,∴2a+b=0,故①正确;∵抛物线y=ax2+bx+c的对称轴为直线x=1,与x轴的一个交点的横坐标在2,3之间,∴与x轴的另一个交点的横坐标在-1,0之间,∴方程ax2+bx+c=0一定有一个根在-1和0之间,故②错误;∵抛物线y=ax2+bx+c与直线y=有两个交点,∴方程ax2+bx+c-=0一定有两个不相等的实数根,故③正确;∵抛物线与x轴的另一个交点的横坐标在-1,0之间,∴a-b+c<0,∵图象与y轴交点的纵坐标是2,∴c=2,∴a-b+2<0,∴b-a>2.故④错误.故选B.
11.k≥3 解析:将抛物线y=x2-6x+12向下平移k个单位长度得y=x2-6x+12-k,∵平移后得到的抛物线与x轴有公共点,∴Δ=b2-4ac≥0,∴(-6)2-4×1×(12-k)≥0,解得k≥3.
12.< 解析:∵y=x2-2x+c,∴抛物线对称轴为直线x=-=1,开口向上,∵|-3-1|>|-2-1|,∴(-2,y1)离对称轴较近,
∴y113. 解析:令CD=x,则AD=AC-CD=8-x,∴BD=AD=8-x,∵∠C=90°,∴BD2=CD2+BC2,∴(8-x)2=x2+42,∴x=3,
∴CD=3,∵AD=BD,∴∠ABD=∠A=α,∴∠CDB=∠A+∠ABD=2α,∴tan 2α=.
14.2.25 解析:如图所示,以AE所在直线为x轴,AB所在直线为y轴建立平面直角坐标系,
根据题意知,抛物线的顶点C的坐标为(1.5,2.5),设抛物线的表达式为y=a(x-1.5)2+2.5,将点B(0,1.5)代入得,2.25a+2.5=1.5,∴a=-.∴抛物线的表达式为y=-(x-1.5)2+2.5,当y=2.25时,-(x-1.5)2+2.5=2.25,解得x=0.75(舍)或x=2.25,∴茶几到灯柱的距离AE为2.25 m.
15.11.5 解析:由题意,知DM∥AC,DC⊥AC,∠MDA=65°,∠MDB=45°.如图,过点B作BE⊥DC,垂足为E.
∵BE⊥CD,BA⊥AC,DC⊥AC,∴∠C=∠BEC=∠CAB=90°.∴四边形CABE是矩形.∴BE=AC=10 m,CE=AB.
∵DM∥AC∥BE,∴∠MDB=∠EBD=45°,∠MDA=∠DAC=65°.在Rt△ACD中,∵tan∠DAC=,
∴DC=tan∠DAC·AC=tan 65°×10≈2.145×10=21.45(m).在Rt△DBE中,
∵tan∠DBE=,∴DE=tan∠DBE·AC=tan 45°×10=1×10=10(m).∴AB=DC-DE=21.45-10=11.45≈11.5(m).
16.解:(1)把A(-1,0)和C(0,3)代入二次函数y=ax2+2x+c中,
得解得
∴二次函数的表达式为y=-x2+2x+3.
(2)如图所示,y=-(x-1)2+4,
x=1时,y的最大值为4,
当-1函数y的取值范围为017.解:(1)∵AC⊥BD,
∴∠ACB=∠ACD=90°.
在Rt△ABC中,cos∠ABC=,
∴AB==10,∴AC==6.
(2)∵BE为AD边上的中线,
∴S△BED=S△ABD.
又∵S△ABD=BD·AC=×12×6=36,
∴S△BED=×36=18.
18.解:(1)根据题意得:
(x-60)(-20x+2 400)=16 000,
解得x1=100,x2=80,
∵尽量给顾客实惠,
∴x=100,不符合题意,舍去.
答:售价应定为80元.
(2)∵每件利润不允许超过每件进价的40%,
∴x-60≤60×40%,解得x≤84,
∴60≤x≤84,
根据题意得w=(x-60)(-20x+2 400)=-20x2+3 600x-144 000=-20(x-90)2+18 000,
∵-20<0,
∴当x≤90时,w随x的增大而增大,
∴当x=84时,w取最大值,最大值为-20×(84-90)2+18 000=17 280(元).
答:售价定为84元时,服装店可获得最大利润,最大利润是17 280元.
19.解:(1)如图:
由题意得:AC⊥CD,BE∥CD,
∴∠EBD=∠BDC=36.87°,
在Rt△BCD中,BD=10 m,
∴CD=BD·cos 36.87°≈10×0.80=8(m),
∴CD的长约为8 m.
(2)在Rt△BCD中,BD=10 m,
∠BDC=36.87°,
∴BC=BD·sin 36.87°≈10×0.6=6(m),
在Rt△ACD中,AD=17 m,CD=8 m,
∴AC==15(m),
∴AB=AC-BC=15-6=9(m),
∵模拟装置从点A以每秒2 m的速度匀速下降到点B,
∴模拟装置从点A下降到点B的时间为
9÷2=4.5(s).
20.解:(1)由题意,将A(-2,0),C(0,-2)代入y=x2+bx+c得
∴
∴二次函数的表达式为y=x2+x-2.
(2)由题意,设P(m,n),
∵点P在第二象限,∴m<0,n>0,
又∵△PDB的面积是△CDB的面积的2倍,
∴=2,=2.
∴=2.
又∵CO=2,
∴n=2CO=4.
由m2+m-2=4,
∴m1=-3,m2=2(舍去).
∴点P坐标为(-3,4).
21.解:(1)∵AB边长为6 dm,最高点C到AB的距离为6 dm.
∴点B的坐标为(6,0),
根据抛物线的对称性可知:顶点C的坐标为(3,6),
设这个抛物线的表达式为y=a(x-3)2+6,
将点(6,0)代入y=a(x-3)2+6,得0=a(6-3)2+6,解得a=-,
∴抛物线的表达式为y=-(x-3)2+6=-x2+4x.
(2)能够实现,
∵点D在抛物线上,
∴可设点D的坐标为t,-t2+4t,
连接DF交CE于点H,如图:
∵四边形CDEF为正方形,
∴HD=HC,DF⊥CE,
∵CE为抛物线的对称轴,点C的坐标为(3,6),
∴点H的坐标为3,-t2+4t,
∴HD=3-t,HC=6--t2+4t=t2-4t+6,
∴3-t=t2-4t+6,
整理得:2t2-9t+9=0,
解得:t=1.5或t=3(不合题意,舍去),
当t=1.5时,-t2+4t=4.5,
∴点D的坐标为(1.5,4.5).
22.解:(1)过点B作BE⊥AC于点E,如图,
根据已知得∠DAB=90°,
∵∠DAC=30°,
∴∠EAB=60°,∠EBA=30°,
∴AE=AB=1 km,BE=AE= km.
∵C在B的北偏西15°方向,
∴∠EBC=90°-30°-15°=45°,
∴△EBC是等腰直角三角形,
∴CE=BE= km,BC=BE=≈2.5(km),
∴BC的长度约为2.5 km.
(2)过点C作CF⊥AD于点F,如图,
由(1)知AE=1 km,CE= km,
∴AC=AE+CE=(1+)km.
在Rt△ACF中,CF=AC= km,AF=CF= km,
∵D在C的北偏西60°方向,
∴∠DCF=30°,
∴DF= km,CD=2DF= km,
∴乙选择的路线长为AD+AB=+2=≈5.2(km);
甲选择的路线长为CD+BC=≈4(km),
∴CD+BC∴甲选择的路线比较近.
23.解:(1)∵二次函数图象经过O(0,0),
A(4,0),B(1,3),
∴将三点坐标代入表达式得
解得:
∴二次函数的表达式为y=-x2+4x.
∵直线经过A,B两点,设直线AB表达式为y=kx+n,
∴将A,B两点坐标代入得
解得
∴直线AB表达式为y=-x+4.
∵点C是直线与y轴交点,
∴令x=0,则y=4,
∴C(0,4).
(2)①∵点P在直线AB上方,如图1,
图1
∴1≤m≤4.
由题知P(m,-m2+4m),D(m,-m+4),
∴PD=yP-yD=-m2+4m+m-4=-m2+5m-4=-m-2+,
∵-1<0,
∴当m=时,PD=是最大值.
②存在.
∵∠PDB=∠ADE,∠ADE=∠ACO,
∴∠BDP=∠ACO,
∵△AOC是直角三角形,
∴要使△BPD与△AOC相似,只有保证△BPD是直角三角形就可以.
(Ⅰ)当△BPD∽△AOC时,如图2,
∵∠AOC=90°,∴∠BPD=90°,
此时BP∥x轴,B、P关于对称轴对称,
∴P(3,3);
图2
(Ⅱ)当△PBD∽△AOC时,如图3,
∴∠PBD=∠AOC=90°,∴AB⊥PB,
∵kAC=-1,∴kBP=1,
∴直线BP的表达式为y=x+2,
联立方程组得
解得或
∴P(2,4).
图3
综上,存在点P使△BPD与△AOC相似,此时点P的坐标为(3,3)或(2,4).
(满分:120分 时间:120分钟)
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图,在4×4的正方形网格中,tan α的值为 ( )
A. B.2 C. D.
2.已知y=(m+1)+2x-3是二次函数,则m的值为 ( )
A.0 B.1 C.-1 D.1或-1
3.在平面直角坐标系xOy中,抛物线的顶点是(1,3),当x>1时,y随x的增大而增大,则抛物线表达式可以是 ( )
A.y=-2(x+1)2+3 B.y=2(x+1)2+3
C.y=-2(x-1)2+3 D.y=2(x-1)2+3
4.抛物线y=-(x+3)(x-2)与x轴的两交点之间的距离是 ( )
A.1 B.3 C.5 D.6
5.在Rt△ABC中,∠C=90°,若sin A=,则cos A的值为 ( )
A. B. C. D.
6.如图1是莲花山景区一座抛物线形拱桥,按图2所示建立平面直角坐标系,得到抛物线表达式为y=-x2,正常水位时水面宽AB为36 m,当水位上升5 m时水面宽CD为 ( )
图1 图2
A.10 m B.12 m C.24 m D.48 m
7.(2024深圳龙岗区模拟)桔槔俗称“吊杆”“称杆”(如图1),是我国古代农用工具,始见于《墨子·备城门》,是一种利用杠杆原理的取水机械.桔槔示意图如图2所示,OM是垂直于水平地面的支撑杆,OM=3 m,AB是杠杆,AB=6 m,OA∶OB=2∶1.当点A位于最高点时,∠AOM=120°.此时,点A到地面的距离为 ( )
图1 图2
A.(2+3)m B.5 m C.6 m D.7 m
8.数学实践小组测量某路段上一处标识脱落的车辆限高杆MN的高度AB,如图,他们先用测角仪在C处测得点A的仰角∠AEG=30°,然后在D处测得点A的仰角∠AFG=45°,已知点C,D,B在同一条直线上,测角仪离地面高度CE=1 m,CD=2 m,则AB高 ( )
A.(+2) m B.(+1) m C.(+3) m D.(+2) m
9.(2024陕西中考)已知一个二次函数y=ax2+bx+c的自变量x与函数y的几组对应值如下表:
x … -4 -2 0 3 5 …
y … -24 -8 0 -3 -15 …
则下列关于这个二次函数的结论正确的是 ( )
A.图象的开口向上 B.当x>0时,y的值随x值的增大而减小
C.图象经过第二、三、四象限 D.图象的对称轴是直线x=1
10.(2024泰安中考)如图所示是二次函数y=ax2+bx+c(a≠0)的部分图象,该函数图象的对称轴是直线x=1,图象与y轴交点的纵坐标是2.则下列结论:①2a+b=0;②方程ax2+bx+c=0一定有一个根在-2和-1之间;③方程ax2+bx+c-=0一定有两个不相等的实数根;④b-a<2.其中,正确结论的个数是 ( )
A.1 B.2 C.3 D.4
二、填空题(本题共5小题,每小题3分,共15分)
11.(2024济宁中考)将抛物线y=x2-6x+12向下平移k个单位长度.若平移后得到的抛物线与x轴有公共点,则k的取值范围是 .
12.已知抛物线y=x2-2x+c,且经过点(-2,y1),(-3,y2),试比较y1和y2的大小:y1 y2.(填“>”“<”或“=”)
13.如图,在Rt△ABC中,∠C=90°,AC=8,BC=4,∠A=α,易知tan α=,小明同学想求tan 2α的值,他在AC上取点D,使得BD=AD,则tan 2α= .
14.如图是一款抛物线形落地灯的示意图,防滑螺母C为抛物线支架的最高点,灯罩D距离地面2.25 m,最高点C距灯柱AB的水平距离为1.5 m,灯柱AB=1.5 m,若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为 m.
15.(2024赤峰中考)综合实践课上,航模小组用无人机测量古树AB的高度.如图,点C处与古树底部A处在同一水平面上,且AC=10 m,无人机从C处竖直上升到达D处,测得古树顶部B的俯角为45°,古树底部A的俯角为65°,则古树AB的高度约为 m.(结果精确到0.1 m;参考数据:sin 65°≈0.906,cos 65°≈0.423,tan 65°≈2.145)
三、解答题(本题共8小题,共75分.解答应写出文字说明、演算步骤或推理过程)
16.(6分)如图,已知二次函数y=ax2+2x+c图象经过点A(-1,0)和点C(0,3).
(1)求该二次函数的表达式;
(2)结合函数图象,直接写出当-1
(1)求AC的长;
(2)求△BED的面积.
18.(8分)某服装店销售一款卫衣,该款卫衣每件进价为60元,规定每件售价不低于进价.经市场调查发现,该款卫衣每月的销售量y(件)与每件售价x(元)满足一次函数关系y=-20x+2 400.
(1)若服装店每月既想从销售该款卫衣中获利16 000元,又想尽量给顾客实惠,售价应定为多少元
(2)为维护市场秩序,物价部门规定该款卫衣的每件利润不允许超过每件进价的40%.设该款卫衣每月的总利润为w(元),那么售价定为多少元时服装店可获得最大利润 最大利润是多少元
19.(10分)(2024广州中考)2024年6月2日,嫦娥六号着陆器和上升器组合体(简称为“着上组合体”)成功着陆在月球背面.某校综合实践小组制作了一个“着上组合体”的模拟装置,在一次试验中,如图,该模拟装置在缓速下降阶段从点A垂直下降到点B,再垂直下降到着陆点C,从点B测得地面点D的俯角为36.87°,AD=17 m,BD=10 m.
(1)求CD的长;
(2)若模拟装置从点A以每秒2 m的速度匀速下降到点B,求模拟装置从A点下降到点B的时间.
参考数据:sin 36.87°≈0.60,cos 36.87°≈0.80,tan 36.87°≈0.75.
20.(10分)(2024福建中考)如图,已知二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴交于点C,其中A(-2,0),C(0,-2).
(1)求二次函数的表达式;
(2)若P是二次函数图象上的一点,且点P在第二象限,线段PC交x轴于点D,△PDB的面积是
△CDB的面积的2倍,求点P的坐标.
21.(10分)如图,是一块抛物线形板材,工人师傅以A为坐标原点,AB边所在直线为x轴,过A点作AB的垂线为y轴,建立平面直角坐标系,根据测量得知AB边长为6 dm,最高点C到AB的距离为6 dm.
(1)求该抛物线的表达式.
(2)工人师傅计划在抛物线形板材上截出一个正方形CDEF,要求D,F两点在抛物线上(D在F的左侧),点E在抛物线的对称轴上,工人师傅的计划能否实现 若能,请你帮助工人师傅在抛物线上找出点D的位置(即求出点D的坐标),若不能,请说明理由.
22.(12分)(2024重庆B卷中考)如图,A,B,C,D分别是某公园四个景点,B在A的正东方向,D在A的正北方向,且在C的北偏西60°方向,C在A的北偏东30°方向,且在B的北偏西15°方向,AB=2 km.
(参考数据:≈1.41,≈1.73,≈2.45)
(1)求BC的长度(结果精确到0.1 km);
(2)甲、乙两人从景点D出发去景点B,甲选择的路线为:D-C-B,乙选择的路线为:D-A-B.请计算说明谁选择的路线较近
23.(13分)如图,在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象经过原点和点A(4,0).经过点A的直线与该二次函数图象交于点B(1,3),与y轴交于点C.
(1)求二次函数的表达式及点C的坐标;
(2)点P是二次函数图象上的一个动点,当点P在直线AB上方时,过点P作PE⊥x轴于点E,与直线AB交于点D,设点P的横坐标为m.
①m为何值时线段PD的长度最大,并求出最大值;
②是否存在点P,使得△BPD与△AOC相似.若存在,请求出点P坐标;若不存在,请说明理由.
【详解答案】
1.B 解析:由题图,tan α==2.故选B.
2.B 解析:由y=(m+1)+2x-3是二次函数,得,解得m=1.故选B.
3.D 解析:由题意得:抛物线的顶点是(1,3),开口向上.故选D.
4.C 解析:∵抛物线y=-(x+3)(x-2)与x轴有两个交点,∴-(x+3)(x-2)=0,解得:x1=-3,x2=2,
∴两个交点坐标是(-3,0),(2,0),∴两个交点之间的距离是5.故选C.
5.A 解析:∵在Rt△ABC中,∠C=90°,sin A=,∴设BC=5k,则AB=13k,根据勾股定理可以得到:AC==12k,∴cos A=.故选A.
6.C 解析:∵AB=36 m,∴当x=18时,y=-×182=-9,当水位上升5 m时,y=-4,把y=-4代入抛物线表达式得:-4=-x2,解得x=±12,此时水面宽CD=24(m).故选C.
7.B 解析:如图,过点O作EF⊥OM,过点A作AG⊥EF于点G,
∵AB=6 m,OA∶OB=2∶1,∴OA=4 m,∵∠AOM=120°,∠EOM=90°,∴∠AOE=30°,在Rt△AOG中,AG=AO·sin 30°=2(m),点A位于最高点时到地面的距离为2+3=5(m),∴点A到地面的距离为5 m.故选B.
8.A 解析:如图,延长EF交AB于点H,
由题意得,HB=DF=CE=1 m,CD=FE=2 m,设HF=x m,则EH=HF+FE=(x+2)m,在Rt△AHF中,∠AFH=45°,
∴∠FAH=45°,∴AH=HF=x m,在Rt△AHE中,tan 30°=,解得x=+1,
∴AB=AH+BH=+1+1=(+2)(m).故选A.
9.D 解析:由题知,解得∴二次函数的表达式为y=-x2+2x.∵a=-1<0,∴抛物线的开口向下.故A选项不符合题意.∵y=-x2+2x=-(x-1)2+1,∴当x>1时,y随x的增大而减小.故B选项不符合题意.令y=0得,-x2+2x=0,解得x1=0,x2=2,∴抛物线与x轴的交点坐标为(0,0)和(2,0).又∵抛物线的顶点坐标为(1,1),∴抛物线经过第一、三、四象限.故C选项不符合题意.∵二次函数表达式为y=-(x-1)2+1,∴抛物线的对称轴为直线x=1.故D选项符合题意.故选D.
10.B 解析:∵抛物线的对称轴为直线x=1,∴-=1,∴b=-2a,∴2a+b=0,故①正确;∵抛物线y=ax2+bx+c的对称轴为直线x=1,与x轴的一个交点的横坐标在2,3之间,∴与x轴的另一个交点的横坐标在-1,0之间,∴方程ax2+bx+c=0一定有一个根在-1和0之间,故②错误;∵抛物线y=ax2+bx+c与直线y=有两个交点,∴方程ax2+bx+c-=0一定有两个不相等的实数根,故③正确;∵抛物线与x轴的另一个交点的横坐标在-1,0之间,∴a-b+c<0,∵图象与y轴交点的纵坐标是2,∴c=2,∴a-b+2<0,∴b-a>2.故④错误.故选B.
11.k≥3 解析:将抛物线y=x2-6x+12向下平移k个单位长度得y=x2-6x+12-k,∵平移后得到的抛物线与x轴有公共点,∴Δ=b2-4ac≥0,∴(-6)2-4×1×(12-k)≥0,解得k≥3.
12.< 解析:∵y=x2-2x+c,∴抛物线对称轴为直线x=-=1,开口向上,∵|-3-1|>|-2-1|,∴(-2,y1)离对称轴较近,
∴y1
∴CD=3,∵AD=BD,∴∠ABD=∠A=α,∴∠CDB=∠A+∠ABD=2α,∴tan 2α=.
14.2.25 解析:如图所示,以AE所在直线为x轴,AB所在直线为y轴建立平面直角坐标系,
根据题意知,抛物线的顶点C的坐标为(1.5,2.5),设抛物线的表达式为y=a(x-1.5)2+2.5,将点B(0,1.5)代入得,2.25a+2.5=1.5,∴a=-.∴抛物线的表达式为y=-(x-1.5)2+2.5,当y=2.25时,-(x-1.5)2+2.5=2.25,解得x=0.75(舍)或x=2.25,∴茶几到灯柱的距离AE为2.25 m.
15.11.5 解析:由题意,知DM∥AC,DC⊥AC,∠MDA=65°,∠MDB=45°.如图,过点B作BE⊥DC,垂足为E.
∵BE⊥CD,BA⊥AC,DC⊥AC,∴∠C=∠BEC=∠CAB=90°.∴四边形CABE是矩形.∴BE=AC=10 m,CE=AB.
∵DM∥AC∥BE,∴∠MDB=∠EBD=45°,∠MDA=∠DAC=65°.在Rt△ACD中,∵tan∠DAC=,
∴DC=tan∠DAC·AC=tan 65°×10≈2.145×10=21.45(m).在Rt△DBE中,
∵tan∠DBE=,∴DE=tan∠DBE·AC=tan 45°×10=1×10=10(m).∴AB=DC-DE=21.45-10=11.45≈11.5(m).
16.解:(1)把A(-1,0)和C(0,3)代入二次函数y=ax2+2x+c中,
得解得
∴二次函数的表达式为y=-x2+2x+3.
(2)如图所示,y=-(x-1)2+4,
x=1时,y的最大值为4,
当-1
∴∠ACB=∠ACD=90°.
在Rt△ABC中,cos∠ABC=,
∴AB==10,∴AC==6.
(2)∵BE为AD边上的中线,
∴S△BED=S△ABD.
又∵S△ABD=BD·AC=×12×6=36,
∴S△BED=×36=18.
18.解:(1)根据题意得:
(x-60)(-20x+2 400)=16 000,
解得x1=100,x2=80,
∵尽量给顾客实惠,
∴x=100,不符合题意,舍去.
答:售价应定为80元.
(2)∵每件利润不允许超过每件进价的40%,
∴x-60≤60×40%,解得x≤84,
∴60≤x≤84,
根据题意得w=(x-60)(-20x+2 400)=-20x2+3 600x-144 000=-20(x-90)2+18 000,
∵-20<0,
∴当x≤90时,w随x的增大而增大,
∴当x=84时,w取最大值,最大值为-20×(84-90)2+18 000=17 280(元).
答:售价定为84元时,服装店可获得最大利润,最大利润是17 280元.
19.解:(1)如图:
由题意得:AC⊥CD,BE∥CD,
∴∠EBD=∠BDC=36.87°,
在Rt△BCD中,BD=10 m,
∴CD=BD·cos 36.87°≈10×0.80=8(m),
∴CD的长约为8 m.
(2)在Rt△BCD中,BD=10 m,
∠BDC=36.87°,
∴BC=BD·sin 36.87°≈10×0.6=6(m),
在Rt△ACD中,AD=17 m,CD=8 m,
∴AC==15(m),
∴AB=AC-BC=15-6=9(m),
∵模拟装置从点A以每秒2 m的速度匀速下降到点B,
∴模拟装置从点A下降到点B的时间为
9÷2=4.5(s).
20.解:(1)由题意,将A(-2,0),C(0,-2)代入y=x2+bx+c得
∴
∴二次函数的表达式为y=x2+x-2.
(2)由题意,设P(m,n),
∵点P在第二象限,∴m<0,n>0,
又∵△PDB的面积是△CDB的面积的2倍,
∴=2,=2.
∴=2.
又∵CO=2,
∴n=2CO=4.
由m2+m-2=4,
∴m1=-3,m2=2(舍去).
∴点P坐标为(-3,4).
21.解:(1)∵AB边长为6 dm,最高点C到AB的距离为6 dm.
∴点B的坐标为(6,0),
根据抛物线的对称性可知:顶点C的坐标为(3,6),
设这个抛物线的表达式为y=a(x-3)2+6,
将点(6,0)代入y=a(x-3)2+6,得0=a(6-3)2+6,解得a=-,
∴抛物线的表达式为y=-(x-3)2+6=-x2+4x.
(2)能够实现,
∵点D在抛物线上,
∴可设点D的坐标为t,-t2+4t,
连接DF交CE于点H,如图:
∵四边形CDEF为正方形,
∴HD=HC,DF⊥CE,
∵CE为抛物线的对称轴,点C的坐标为(3,6),
∴点H的坐标为3,-t2+4t,
∴HD=3-t,HC=6--t2+4t=t2-4t+6,
∴3-t=t2-4t+6,
整理得:2t2-9t+9=0,
解得:t=1.5或t=3(不合题意,舍去),
当t=1.5时,-t2+4t=4.5,
∴点D的坐标为(1.5,4.5).
22.解:(1)过点B作BE⊥AC于点E,如图,
根据已知得∠DAB=90°,
∵∠DAC=30°,
∴∠EAB=60°,∠EBA=30°,
∴AE=AB=1 km,BE=AE= km.
∵C在B的北偏西15°方向,
∴∠EBC=90°-30°-15°=45°,
∴△EBC是等腰直角三角形,
∴CE=BE= km,BC=BE=≈2.5(km),
∴BC的长度约为2.5 km.
(2)过点C作CF⊥AD于点F,如图,
由(1)知AE=1 km,CE= km,
∴AC=AE+CE=(1+)km.
在Rt△ACF中,CF=AC= km,AF=CF= km,
∵D在C的北偏西60°方向,
∴∠DCF=30°,
∴DF= km,CD=2DF= km,
∴乙选择的路线长为AD+AB=+2=≈5.2(km);
甲选择的路线长为CD+BC=≈4(km),
∴CD+BC
23.解:(1)∵二次函数图象经过O(0,0),
A(4,0),B(1,3),
∴将三点坐标代入表达式得
解得:
∴二次函数的表达式为y=-x2+4x.
∵直线经过A,B两点,设直线AB表达式为y=kx+n,
∴将A,B两点坐标代入得
解得
∴直线AB表达式为y=-x+4.
∵点C是直线与y轴交点,
∴令x=0,则y=4,
∴C(0,4).
(2)①∵点P在直线AB上方,如图1,
图1
∴1≤m≤4.
由题知P(m,-m2+4m),D(m,-m+4),
∴PD=yP-yD=-m2+4m+m-4=-m2+5m-4=-m-2+,
∵-1<0,
∴当m=时,PD=是最大值.
②存在.
∵∠PDB=∠ADE,∠ADE=∠ACO,
∴∠BDP=∠ACO,
∵△AOC是直角三角形,
∴要使△BPD与△AOC相似,只有保证△BPD是直角三角形就可以.
(Ⅰ)当△BPD∽△AOC时,如图2,
∵∠AOC=90°,∴∠BPD=90°,
此时BP∥x轴,B、P关于对称轴对称,
∴P(3,3);
图2
(Ⅱ)当△PBD∽△AOC时,如图3,
∴∠PBD=∠AOC=90°,∴AB⊥PB,
∵kAC=-1,∴kBP=1,
∴直线BP的表达式为y=x+2,
联立方程组得
解得或
∴P(2,4).
图3
综上,存在点P使△BPD与△AOC相似,此时点P的坐标为(3,3)或(2,4).
同课章节目录
